电驱动系统再生制动工况动力学特性研究*

刘 坤，杜长虹，吴 维，卢国成，苑士华

（1.北京理工大学机械与车辆学院，北京100081；2.重庆长安汽车股份有限公司，重庆400023）

前言

为了更好地发挥驱动电机的性能、减轻车身质量，驱动电机+传动机构形式的电驱动系统在电动汽车领域的应用越来越广泛［1］。电驱动系统省略了变矩器和离合器等减振元件，表现为欠阻尼系统，使得轮胎扭转特性对电驱动系统动力学特性的影响更加突出［2］。为提升电动汽车行驶里程，再生制动技术的应用越来越广泛，再生制动过程中，电磁转矩随车速变化，在内部和外部时变激励综合影响下，电驱动系统的机电耦合动力学特性更加复杂。

基于多自由度动力学模型，主要考虑驱动系统中一些非线性因素的影响。Qiao等［3］在考虑时变啮合刚度（time varying mesh stiffness，TVMS）的基础上分析了柔性轴对传动机构动态响应的影响，其研究的传动轴太长，在结构紧凑的电驱动系统上使用并不广泛。Kubur等［4］给出多级传动通用的动力学模型，考虑了中间轴上两个齿轮位置角的影响，但未考虑中间轴的扭转耦合。有学者引入分形理论，修正了现有的齿侧间隙模型，得到了计及齿面微观特征的齿轮动力学响应［5］。周世华等［6］建立了8自由度的齿轮-转子-轴承模型，探讨了转速和误差波动对动力学响应的影响，结果表明：传动机构的非线性动力学特性归因于内部激励和外部激励的相互作用。胡纪滨等［7］建立了考虑电磁激励的机电耦合扭振模型，通过注入谐波电流降低机电系统的扭振。重庆大学秦大同教授课题组［8］对电驱动系统的研究比较深入，分析了考虑机电耦合时异步驱动电机和行星齿轮传动机构的载荷特性，表明在变速变载工况下机电耦合效应不可忽略。刘浩［9］等建立了考虑轮胎扭转特性的驱动系统扭转模型，但未深入分析轮胎扭转特性对电驱动系统固有特性的影响。

通过上述文献可知，现有研究大多关注稳态时传动机构内部激励对动力学响应的影响，对于瞬态的分析也只研究了驱动工况。本文中在计及静态传动误差、齿侧间隙、TVMS和支撑轴承的基础上，建立永磁同步电机-两级传动机构-轮胎的多自由度耦合模型，通过试验验证模型的准确性；分析了再生制动工况下轮胎扭转特性和不同再生制动转矩对电驱动系统动力学特性的影响，本研究可为电驱动系统动态载荷研究和寿命预测提供理论指导。

1 电驱动系统机电耦合模型

电驱动系统示意图如图1所示，主要包含驱动电机、两级斜齿轮减速传动机构、轴承以及车轮。齿轮一和电机转子在输入轴上，齿轮二、三共同在中间轴上，齿轮四在输出轴上。传动机构输出轴与半轴共同使用一根轴。

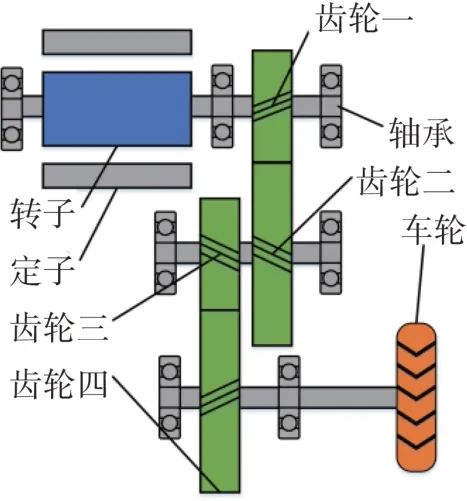
图1 电驱动系统简图

1.1 驱动电机模型

电动汽车由永磁同步电机驱动，采用Clark和Park变换建立交直轴坐标系下驱动电机电压方程和转矩方程：

式中：u、i和L分别为电压、电流和电感，下标d、q代表交直轴；rs为电枢电阻；θr为转子扭转角度；ψf为永磁磁链；pn为转子极对数；Te为驱动电机的电磁转矩。

只考虑驱动电机的机械振动，忽略电磁效应引起的振动，通过Te将电机的电磁模型与机械系统的受迫扭转模型联立起来。电机转子的扭转动力学模型为

式中：Ir为电机转子和轴的转动惯量之和；θg1为齿轮一的扭转角度；ktin、ctin分别为传动机构输入轴的扭转刚度和阻尼。

1.2 斜齿轮啮合力模型

齿轮的TVMS是导致传动机构非线性动力学响应的重要因素，目前主要使用能量法［10］、接触线法［11］和有限元法［12］计算TVMS。能量法包含积分项计算较慢，不适用于长时间的动力学分析，而有限元法与动力学模型耦合复杂。因此，使用接触线法计算TVMS。

设第i条接触线与斜齿轮前端面交点到进入端的距离为u：

式中：θm为齿距角，θm=2π/Zg1，Zg1为齿轮一齿数；pbt为端面基圆齿距。

第i条接触线长度为

式中：βb为基圆螺旋角；εα为端面重合度；εβ为轴向重合度；εγ为总重合度。

可求得综合啮合刚度为

式中：Nb为同时啮合的接触线数目；Ki()θg1为沿接触线单位长度的啮合刚度［11］。

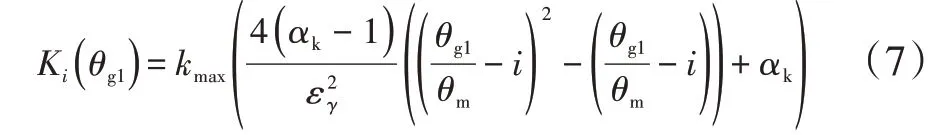
式中：kmax为单齿最大啮合刚度，可由ISO 6336—1获得；αk为材料系数。

可定义啮合线方向上的相对位移δm和啮合力Fm为

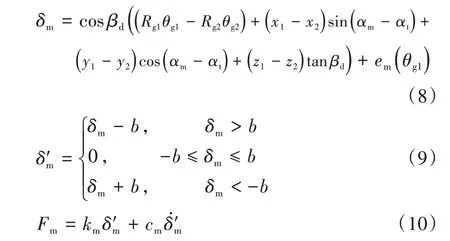
式中：θg2为齿轮二扭转角度；Rg1和Rg2分别为齿轮一、二的基圆半径；x1、y1、z1、x2、y2和z2分别为齿轮一、二的切向、径向和轴向位移；em（θg1）为静态传动误差；αt为端面分度圆压力角；αm为两个齿轮副中心连线与垂直方向的夹角；βd为分度圆螺旋角；cm为啮合阻尼；b为一半的齿侧间隙。

将啮合力分解到切向（x）、径向（y）和轴向（z）：

1.3 两级传动机构动力学模型

两级传动机构动力学模型如图2所示，ktmid、ktout、ctmid、ctout分别为传动机构中间轴和输出轴的扭转刚度和阻尼；kbi1x、cbi1x分别为输入轴轴承切向支承刚度和阻尼，其他轴命名方式类似。

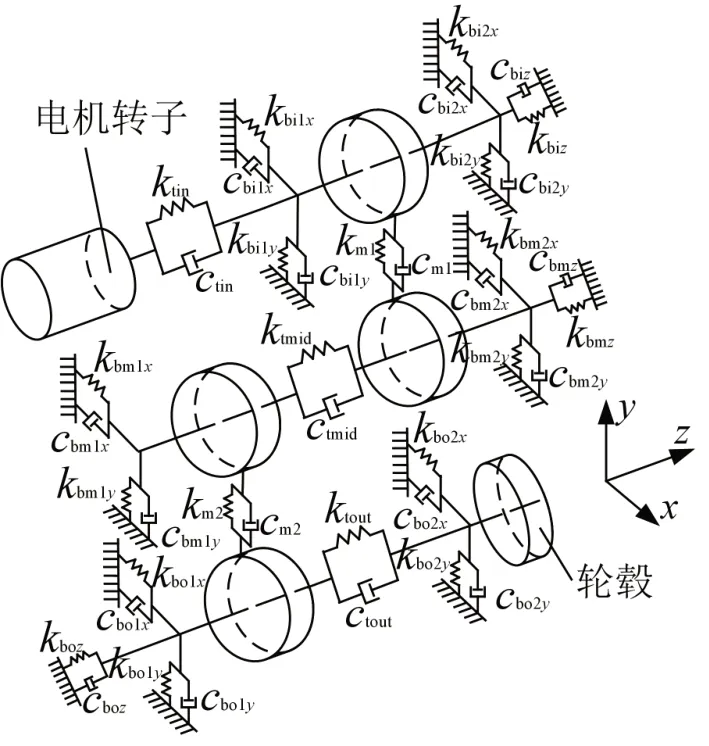
图2 传动机构动力学模型

结合前面计算的啮合力模型，由拉格朗日方程推导出系统的平移运动方程为

式中：mg1~mg4为齿轮一~四质量；kbix、kbmx和kbox分别为输入轴、中间轴和输出轴齿轮原点处切向的等效支承刚度。kbix=kbi1x+kbi2x，同理可得y、z方向和其他轴的等效支承刚度和阻尼。

驱动系统扭转运动方程为

式中：Ig1~Ig4为齿轮一~四的旋转惯量；θg3、θg4、Rg3和Rg4分别为齿轮三、四的扭转角度和基圆半径；θa为轮毂转动角度；Fm1为一级啮合力；Fm2为二级啮合力。

1.4 轮胎模型

作用在车轮上的道路阻力由滚动阻力、坡道阻力和空气阻力组成：

式中：f为滚动摩擦因数；mt为车辆总质量；g为重力加速度；α为坡度角；CD为空气阻力系数；A为汽车迎风面积；v为汽车行驶速度。

为充分考虑车辆的纵向运动，忽略轮胎的侧向和垂向运动，借鉴“刷子”模型，将轮胎模型处理为刚性的轮毂和弹性的胎体，轮胎模型如图3所示。轮胎的扭转动力学模型见式（15）。

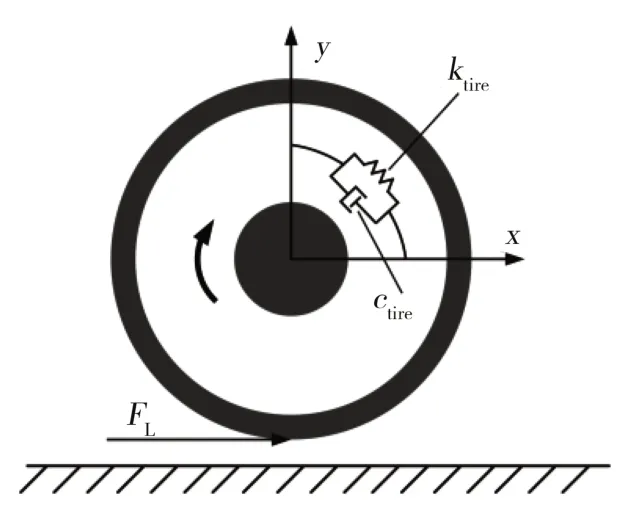
图3 轮胎动力学模型

式中：θb为胎体转动的角度；ktire为轮胎的扭转刚度；ctire为轮胎的扭转阻尼；Rt为轮胎的滚动半径；Ia为轮毂的转动惯量；λ为旋转质量换算系数。

2 模型验证

TVMS难以实际测量，因此与齿轮有限元接触模型计算结果进行了对比，结果如图4所示。解析计算结果与有限元结果吻合良好，两种方法的均值和幅值变化规律基本相同。

图4 基于不同方法的TVMS对比

建立了驱动系统模型试验台架，如图5所示。二级减速器中齿轮齿数分别为16、52、23、71。将SAEC00X5型加速度传感器放置在一级齿轮轴承处，使用PCI⁃4716采集卡及配套软件将采集得到的振动加速度导出分析。试验工况设定为输出转速230 r/min，负载转矩10 N·m。

图5 驱动系统试验台

输入轴轴承处振动加速度的计算结果与试验结果对比如图6所示，试验结果中时域信号为原始试验信号，频域信号为滤波后的结果。

图6 试验结果与计算结果对比

计算结果中主要频率成分为一级齿轮啮频fm1（fm1=615 Hz）、二级齿轮啮频fm2（fm2=272 Hz）、2fm1、3fm1和4fm1，这与试验结果基本相符。但实际运行中还可能存在齿轮偏心、轴不对中、负载波动和噪声干扰等因素，计算得到的振动加速度幅值小于实际测量得到的结果，试验结果频域中也包含一些噪声成分。一级齿轮啮频及其倍频成分占比较高，这是由于测点位置与一级齿轮距离较近，振动信号衰减较少。所建解析模型能够反映系统的动力学特性，可进一步用于电驱动系统的动力学分析。

3 结果与讨论

轮胎和车身参数见表1，驱动系统参数见表2。利用Runge⁃Kutta法对模型进行数值求解。

表1 轮胎/车身参数

表2 电驱动系统参数

3.1 轮胎扭转特性影响规律

易引起驱动系统共振的主要为前几阶固有频率，计算得到的是否考虑轮胎扭转刚度的前5阶固有频率见表3。

表3 电驱动系统固有频率

不考虑轮胎扭转特性时，驱动系统的0阶模态为刚体运动，考虑轮胎扭转特性后，受轮胎扭转刚度约束作用，系统增加了1阶新模态，且1阶固有频率也有所增加。图7为系统0阶和1阶振型图，考虑轮胎扭转特性后，0阶模态主要为扭转运动，各构件相对振幅从电机转子按高速级向低速级递减。1阶振型中，轮毂相对扭转振幅增大，各齿轮振幅不同程度减小，齿轮四减小了0.031 18，齿轮三减小了0.023 1，齿轮二减小了0.010 6，齿轮一减小了0.006 6，振幅减小程度从低速级向高速级递减，表明在1阶模态下，轮胎能够分担一部分传动机构的载荷。

图7 电驱动系统振型图

车辆初速度为80 km/h，在2 s时驱动电机输出20 N·m再生制动转矩，是否考虑轮胎扭转特性的一级齿轮载荷如图8所示。两种情况下一级齿轮载荷基本相同。动载荷呈随车速减小而逐渐减小的趋势，但在67.2、41.3、33.2、16.7和11.2 km/h处出现了数个共振区，由图8（b）可知，主要是由二级齿轮啮频fm2、fm2边频、2fm2、4fm2、6fm2激发了2阶固有频率产生。电磁转矩频率fe、一级齿轮啮频fm1和fm2的其他倍频也激发了2阶固有频率产生了幅值较小的共振区。一级齿轮中受到二级齿轮啮频影响较大，可能是由于齿轮二、三振动位移相同，而齿轮三主要受二级齿轮载荷影响。

图8 齿轮载荷对比

是否考虑轮胎扭转特性载荷不同点主要在电磁转矩反向时刻，见图8（c）。在反向时刻除受外部和内部激励影响产生的强迫振动外，传动机构载荷还受转矩突变激励产生了瞬态自由衰减振动，不考虑轮胎扭转特性时，自由振动fn1频率成分对应的幅值较大，对应1阶固有频率。考虑轮胎扭转特性后，自由振动的频率增加了fn0频率成分，对应由轮胎扭转特性产生的0阶固有频率，表明系统瞬时响应主要由轮胎产生的0阶模态和电驱动系统产生的1阶模态主导，两种固有频率产生的振动使电驱动系统动载荷瞬间增大。由轮胎扭转特性参数改变（0.5ktire~2ktire）带来的固有频率和振型改变很小，导致载荷变化也很小。

结合图7（b）可知，转矩突变后，轮毂和齿轮四反向扭振，可能在半轴上产生较大的扭转切应力，考虑轮胎扭转特性能够为准确计算半轴疲劳损伤提供帮助。

3.2 再生制动转矩影响规律

驱动电机分别输出再生制动转矩5、40、80和120 N·m，一级齿轮载荷的时域响应和频域响应如图9所示。图9（a）为载荷分布的上下包络线，图9（b）为自由振动时的频域响应。再生制动转矩为5 N·m时，传动机构持续发生齿轮双侧拍击现象，且齿背侧的拍击力大于齿面侧的拍击力，直到车速降至30 km/h后，传动机构动载荷减小，只在共振区发生拍击。

图9 不同再生制动转矩下齿轮载荷

再生制动转矩为40 N·m时，驱动电机对传动机构施加的外力增大到齿轮能够保持齿背啮合，只在共振区出现拍击现象。再生制动转矩增加至80和120 N·m时，67.2和33.2 km/h共振区的动载荷显著增大。再生制动转矩为80 N·m时，67.2 km/h处载荷幅值为5 534 N，33.2 km/h处的载荷幅值为7 393 N；再生制动转矩为120 N·m时，67.2 km/h处载荷幅值为7 722 N，33.2 km/h处的载荷幅值为6 733 N。再生制动转矩增加到一定程度后，动载荷幅值不再随转矩的增加而增加。但自由振动的持续时间和动载荷幅值随再生制动转矩的增加而持续增加。由图9（b）可知，是由于fn0和fn1对应载荷的持续时间和幅值增大。

再生制动转矩较小时，发生齿轮拍击现象，可能会产生较大噪声，而再生制动转矩较大时动载荷较大，降低了电驱动系统使用寿命。应尽量避免使用较小的再生制动转矩，在共振区通过减小再生制动转矩、增加机械制动转矩维持制动力不变的同时减小传动机构的动载荷。

4 结论

在考虑静态传动误差、齿侧间隙和时变啮合刚度等因素的基础上，建立了多自由度的永磁同步电机-斜齿轮二级传动机构-轮胎耦合动力学模型，通过试验验证了模型的准确性。研究结果表明：

（1）轮胎扭转特性使得系统刚性模态转变为扭转模态，并减小了系统1阶模态相对振幅；

（2）轮胎扭转特性影响电磁转矩反向时刻传动机构的动载荷，再生制动转矩较小时，传动机构在高速时发生长时间齿轮拍击现象；

（3）随着再生制动转矩的增加，拍击现象逐渐消失，但自由振动时的动载荷和持续时间逐渐增大。