基于改进Hough变换的指针式仪表识别方法

李 娜， 王 军,2， 董兴法*， 石绍鹏

(1. 苏州科技大学 电子信息工程学院,江苏 苏州 215009；2. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

由于指针式仪表易实现、维护成本低等特点，所以常用于电力、化工、石油等行业。变电站电力系统常处于高压危险的环境中，人工读取仪表示数具有工作量大、容易疲劳的缺点，导致识别效率低、误差大、危险系数高，因此利用机器视觉、图像处理等手段，自动检测仪表位置和读取仪表示数，提高了读取仪表示数的准确度[1-2]。目前国内仪表读数识别系统究存在识别速度慢、识别数值不精确等问题，还需进一步完善。

目前研究人员对仪表识别提出了一些研究算法。李全鹏等提出一种基于三次样条插值的指针式仪表图像分割方法，提取包含指针的圆形区域作为信息图，对信息图进行图像分割，有效解决了指针阴影问题[3]。Zheng等提出一种基于Hough变换的读数识别方法，利用Hough变换读取角度识别的原理，对仪表指针角度与刻度的线性关系进行计算示数，但该方法Hough变换计算量大、识别速度慢的缺点[4]。童伟圆等建议使用不同参数的模板来匹配指针，克服了不均匀照明、背景干扰、影响因素，但这种方法对实际应用没有优势，应用复杂，识别准确性不高[5]。钟志伟等提出了累计概率霍夫变换方法识别仪表，较好地解决了光照不均匀问题，但还存在参数难调、计算量大、识别速度慢等问题[6]。Yang提出了一种基于圆的区域累积直方图(CRH)方法来精确定位指针，对照明具有鲁棒性[7]。

本文提出一种改进的Hough变换算法提取仪表指针，采用Otsu算法自适应阈值分割仪表图像，舍弃较小像素值，反复计算分割阈值，从而获得最佳二值图像，能较好地解决不均匀光照问题，再通过改进Hough变换算法结合圆心约束检测仪表指针中心像素点。该算法对于指针式仪表检测识别具有准确性高和速度快的优点。

2 仪表图像识别算法流程

根据仪表图像特点，对采集到的图像进行预处理，排除仪表图像中其他物品干扰，增强仪表指针区域特征。使用Otsu算法分割出仅属于指针区域的像素，再使用改进的Hough检测仪表指针，然后根据角度法计算输出仪表示数。具体算法流程如图1所示。

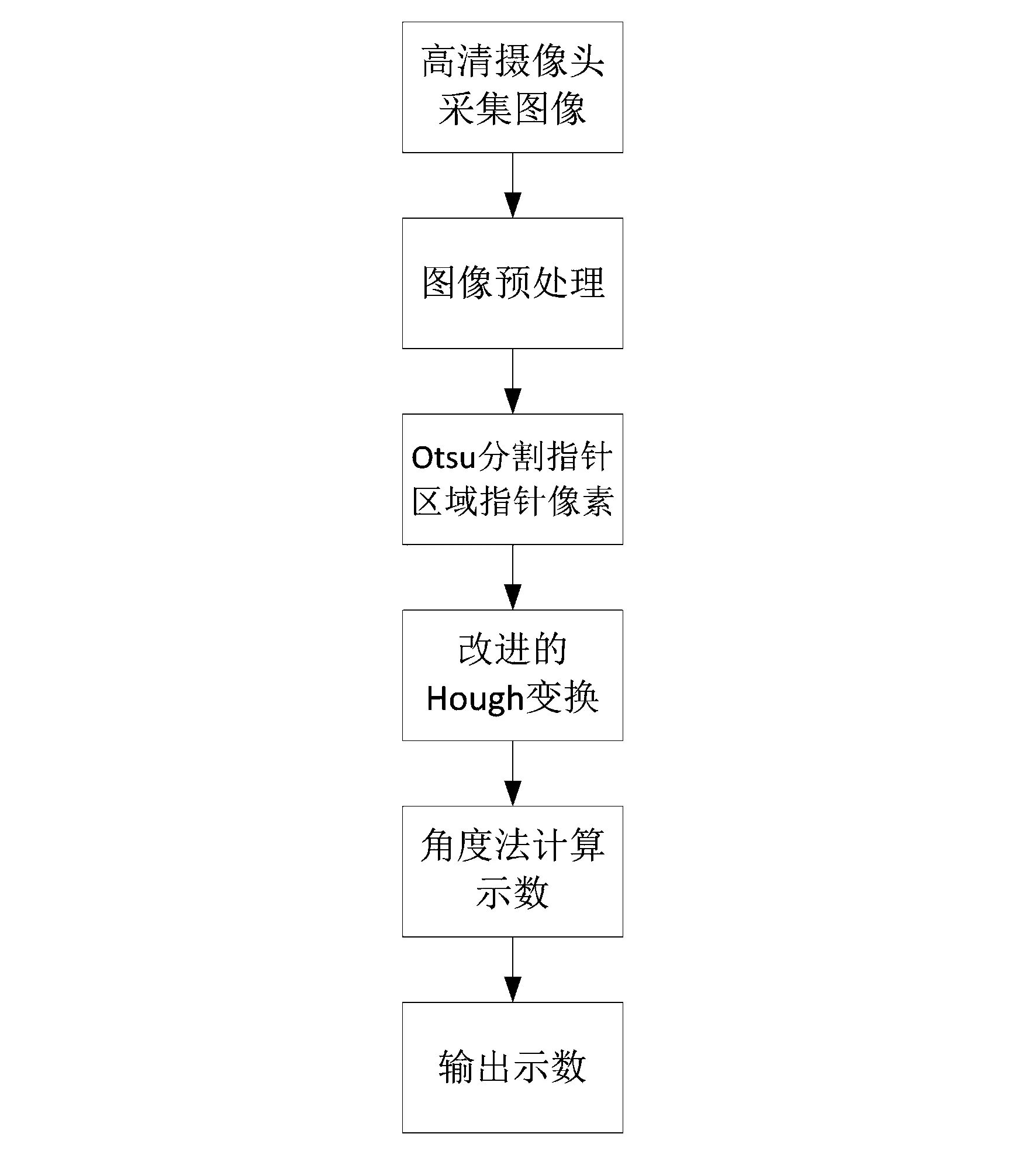
图1 算法流程图 Fig 1 Algorithm flow chart

2.1 仪表图像预处理

在变电站电力系统中，通过高清摄像头采集图像，通过无线传输将仪表图像传给电脑进行图像处理[8]，由于光照强度不同、背景干扰等外围环境的不定因素，采集到的图像中会包含大量噪声。因此对采集的图像进行预处理，通过图像灰度、滤波、增强来突出仪表指针特征[9]。图像滤波采用高斯滤波，对仪表图像有较好的滤波效果，如图2所示，采用灰度拉伸的形态学黑帽运算增强图像对比度，如图3所示。

图2 高斯滤波后的图像Fig.2 Gaussian filtered image

图3 形态学黑帽运算Fig.3 Morphology black hat operation

2.2 仪表图像二值化

由于采集到的仪表图像受光照强度的影响，图片的明暗程度不一样，因此本文采用最大类间方差(Otsu)方法[10]进行自适应二值化处理。

假设前景与后景的分割阈值为T，前景像素点数占图像像素比例为ω0，平均灰度为μ0，后景像素点数占图像像素比例为ω1，平均灰度为μ1，图像的总平均灰度为μ，前景与后景的类间方差为δ，表达式如公式(1)、(2)所示。

μ=ω0×μ0+ω1×μ1

(1)

δ=ω0×(μ-μ0)2+ω1×(μ-μ1)2

(2)

当式(2)中的δ达到最大值时，对应的T就是最佳分割阈值。

根据指针式仪表图像特点，指针区域与背景区域有明显区别，因此可以舍弃影响指针区域分割的背景区域像素值，重复使用Otsu算法，来获取最佳阈值，具体实施步骤如下：

(1)对于图像h×w，将图像的平均灰度值μ作为初始阈值T，进行图像分割。

(2)针对不同光线的图像使用Otsu分割处理，记录其最佳类间方差值，相近的类间方差计算平均值，这些平均值在一定区间内表示为d[d1,d2]，如果类间方差在d范围内，则现在二值图像是最佳二值图像，否则做第三步。

(3)使用初始阈值T进行分割后，记录此时的前景ω0和背景ω1的像素位置，舍弃ω1的像素值，将第一次分割后前景ω0的图像，再次使用Otsu得到分割阈值T。重复步骤(2)直到Otsu值在d范围内，得到最佳二值图像，如图4所示。

图4 本文Otsu算法的二值化图像Fig.4 Otsu algorithm binary image in this paper

3 基于Hough变换检测仪表指针

Hough变换直线检测计算量较大，随着像素点数的增加，计算量也呈线性增加[11]，因此减少Hough变换检测的像素点数并对真正需要检测的像素点进行精准计算，是本文重点研究内容。

仪表读数是以指针中心线对应的刻度数值为准[12]。在Hough变换直线检测中，选取指针区域的中心点，指针经过表盘圆心，这些中心点与表盘圆心有共同的偏转角度，即在极坐标中将这些中心点限定在圆点对应的曲线上。通过这些操作，可以极大地减少Hough变换计算量。

3.1 Hough变换检测原理

Hough变换直线检测的基本原理是：检测直线上一点对应极坐标的一条曲线，直线上所有点对应极坐标所有曲线都相交于一点，相交的这个点对应的直线就是要检测的直线[13],如图5所示。

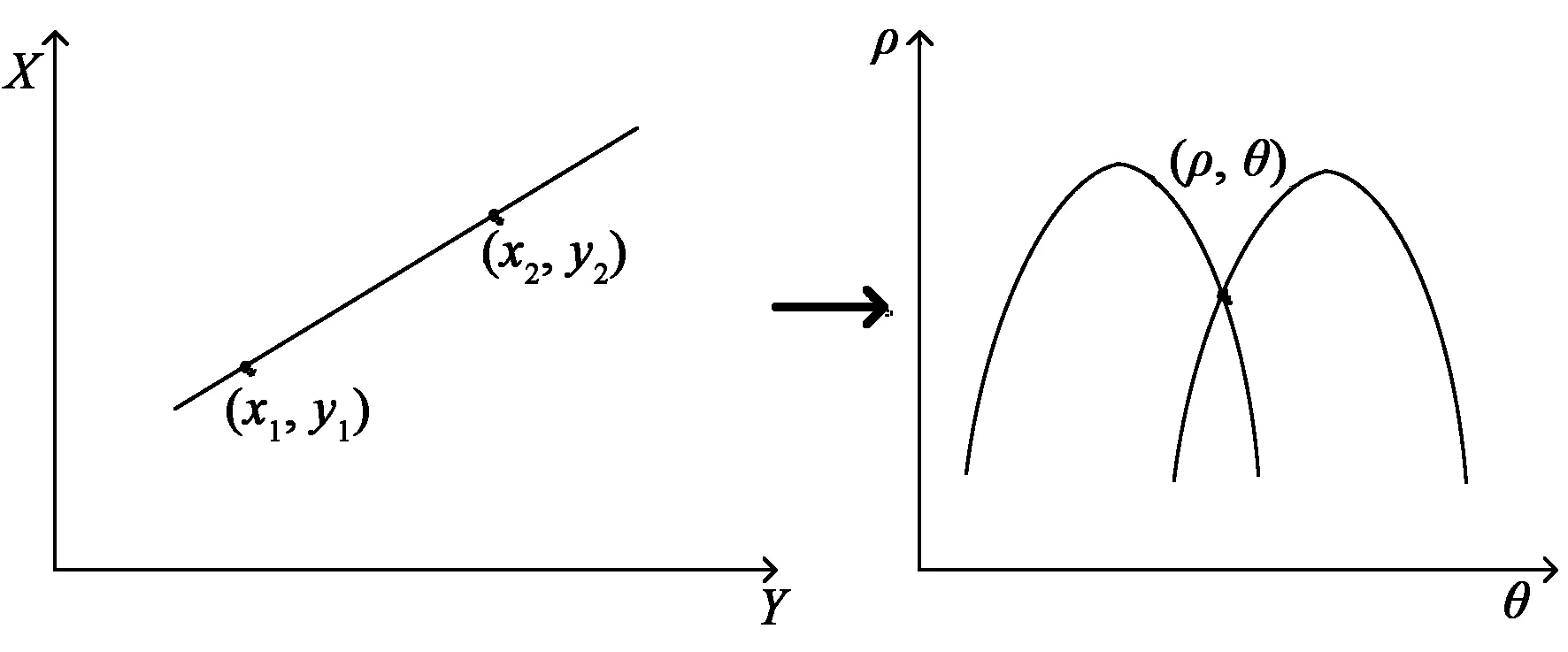
图5 直角坐标到极坐标的转换。(a)直角坐标；(b)极坐标。Fig.5 Conversion from rectangular coordinates to polar coordinates. (a)Cartesian coordinates； (b) Polar coordinates.

假设在原始图像空间(x,y)直线方程为:

y=kx+b

(3)

图像空间和参数空间之间建立对偶变换:

ρ=xcosθ+ysinθ

(4)

Hough变换直线检测转换成极坐标点的检测，只要进行点个数累加就能实现直线检测。

3.2 表盘圆心定位

对表盘圆心坐标的计算，本文提出用垂直平分线来确定表盘圆心，首先在模板图像中确定仪表盘轮廓上3点分别是A、B、C，模板图像的3个点对应实时采集图像的3点,原理如图6所示。

图6 垂直平分线确定表盘中心原理Fig.6 Principle of the vertical bisector to determine the center of the dial

连接BC和AC，找这两条线的垂直平分线。BC的垂直平分线与BC相交于点M，AC的垂直平分线与AC相交于点N,两条垂直平分线相交于一点O，这个点O就是仪表盘圆心，点M和N也是圆心分别在BC和AC线上的投影，记A、B、C坐标分别为A(AX,AY)，B(BX,BY)，C(CX,CY)。因此在参数空间中相交的这一点就是圆心(ρ0，α0),计算M和N的坐标为：

(5)

(6)

(7)

(8)

根据垂直向量相乘等于零的方法计算出圆心坐标：

(9)

.

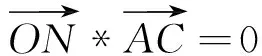
(10)

3.3 改进Hough 变换检测指针

表盘圆心定位之后，将提取的指针区域二值化图像分成若干行，对每一行像素灰度值进行检测。表盘圆心定位后，将提取的指针连通区域分成若干行，然后对每一行像素灰度值进行检测，判断是否为连通区域特征点。将每一行的特征点检测完成后，取这一行连通区域中心点，中心点选取方法如下：

如图7所示，假设有两条平行线l1、l2，选取平行线两边同一水平线两点，分别为A、B，取AB中点P，过P点做一条分别垂直于l1、l2的垂线，垂线的交点为C、D。PD=PC，P点到两条线的距离相等，因此P点就是我们要选取的中心点。

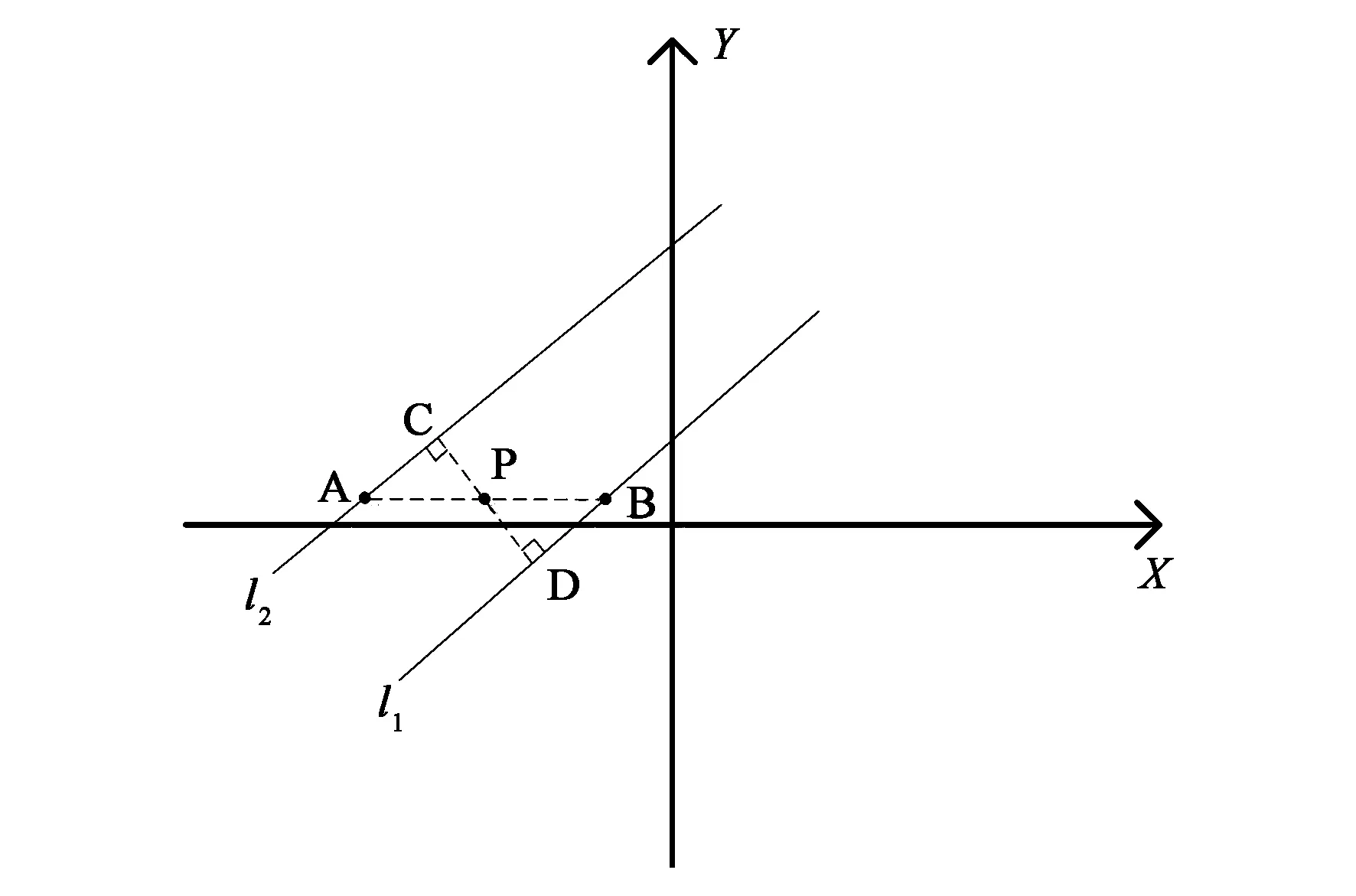
图7 目标区域中心点示意图Fig.7 Schematic diagram of the center point of the target area

指针区域中心点选取之后，结果如图8所示。

图8 中心点选取结果图Fig.8 Center point selection results

改进的Hough变换检测指针连续区域线段的中心点，结合圆心共线的方法，极大地减少了计算量，提高了检测速度。

具体步骤：

(1)假设输入图像h×w,集合W≠φ。

(2)将前期处理过的仪表图像进检测，检测到前景的这个区域有k段，每段像素设为an∈(1,2,......w)。

(3)将每段像素an与这段的指针宽度像素An比较，当an≤An时，标记第n段的像素中心点，将这些中心点记入集合W中。否则执行第二步。

(4)将W中的点限定在圆点对应的曲线上，进行Hough变换检测。

通过以上流程检测到指针后，获得指针偏转角度α，即指针与表盘零刻度的夹角。通过偏转角度与仪表示数的线性关系，计算仪表的读数。将表盘圆心设为图像直角坐标系的原点，如图9所示。

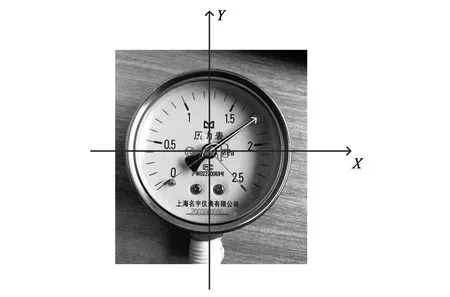
图9 图像直角坐标系Fig.9 Image rectangular coordinate system

压力表范围为0～2.5 Pa，指针与x轴之间的夹角范围为-45°≤α≤225°。假设指针读数获得的是t，得出以下线性关系：

(11)

根据线性关系求出即为指针示数t。

4 实验结果分析

本实验运行硬件环境为以运行内存8 G，CPU为AMD FX-9800P，64位win10操作系统。软件环境为Opencv计算机视觉库VS2019运行环境。

4.1 表盘圆心定位误差因素分析

对于本文提出的方法，仪表示值准确度与圆心检测准确度相关。当拍摄角度不同时，表盘形状会更偏向于椭圆，会对表盘圆心定位的准确性产生一定影响。

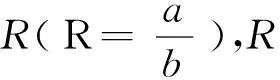
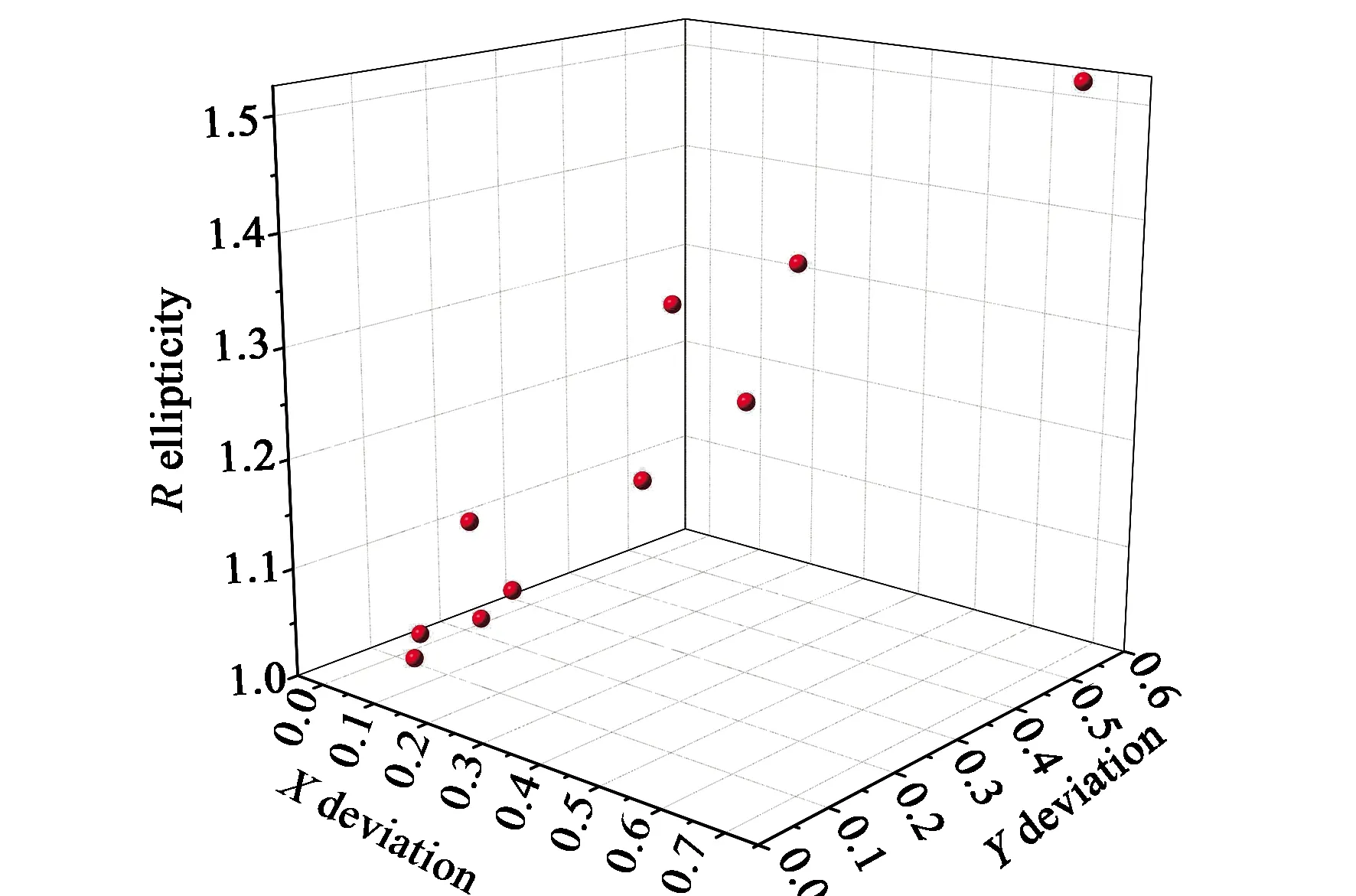
图10 椭圆率对圆心坐标偏差的影响Fig.10 Influence of ellipticity on the deviation of circle center coordinates

从图10可以看出，R越接近于1，圆心定位越准确，R越大则圆心坐标偏差波动越大。对于这一影响因素，圆心坐标定位后期将考虑选取多个点进行计算从减小误差。

4.2 仪表识别实验结果

采用本文所提出的算法，使用Otsu算法进行图像二值化。分别在正常光照条件下不同角度拍摄仪表图像，光线暗亮程度都会影响仪表图像处理。图11是在光线暗的情况下，标准Otsu算法和本文提出的Otsu算法的二值化图像比较，图12是在光线亮的情况下，标准Otsu算法和本文提出的Otsu算法的二值图像比较。

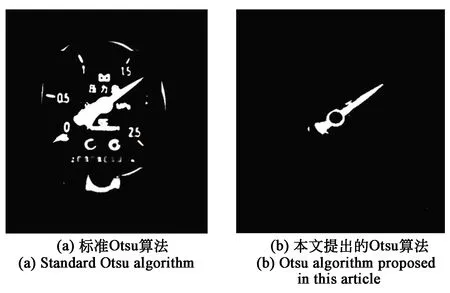
图11 光线暗条件下两种算法对比图Fig.11 Comparison of the two algorithms under dark conditions

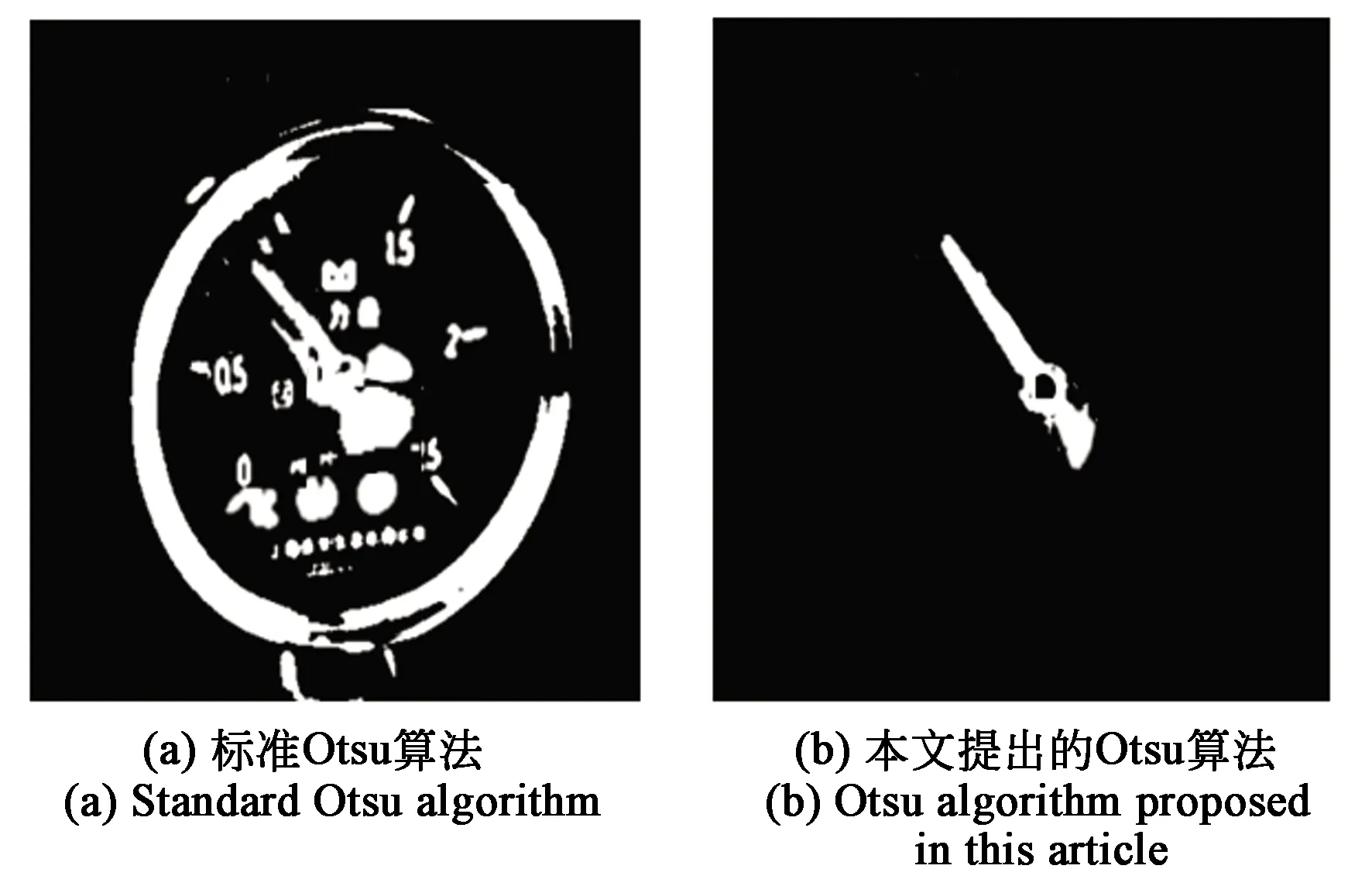
图12 光线亮条件下两种算法对比图Fig.12 Comparison of the two algorithms under bright light conditions

经过仪表图像二值化之后，利用改进Hough变换结合圆心约束检测指针，结果如图13所示。

图13 改进Hough变换检测结果图 Fig.13 Diagram of improved Hough transform detection result

仪表读数实验结果如表1所示。在系统中，对仪表角度识别误差要求在3°以内，相对于读数要求在±0.066 7 MPa以内。改进算法的绝对误差在0.02 MPa左右，满足系统要求，也满足仪表最小刻度0.1 MPa的精度。

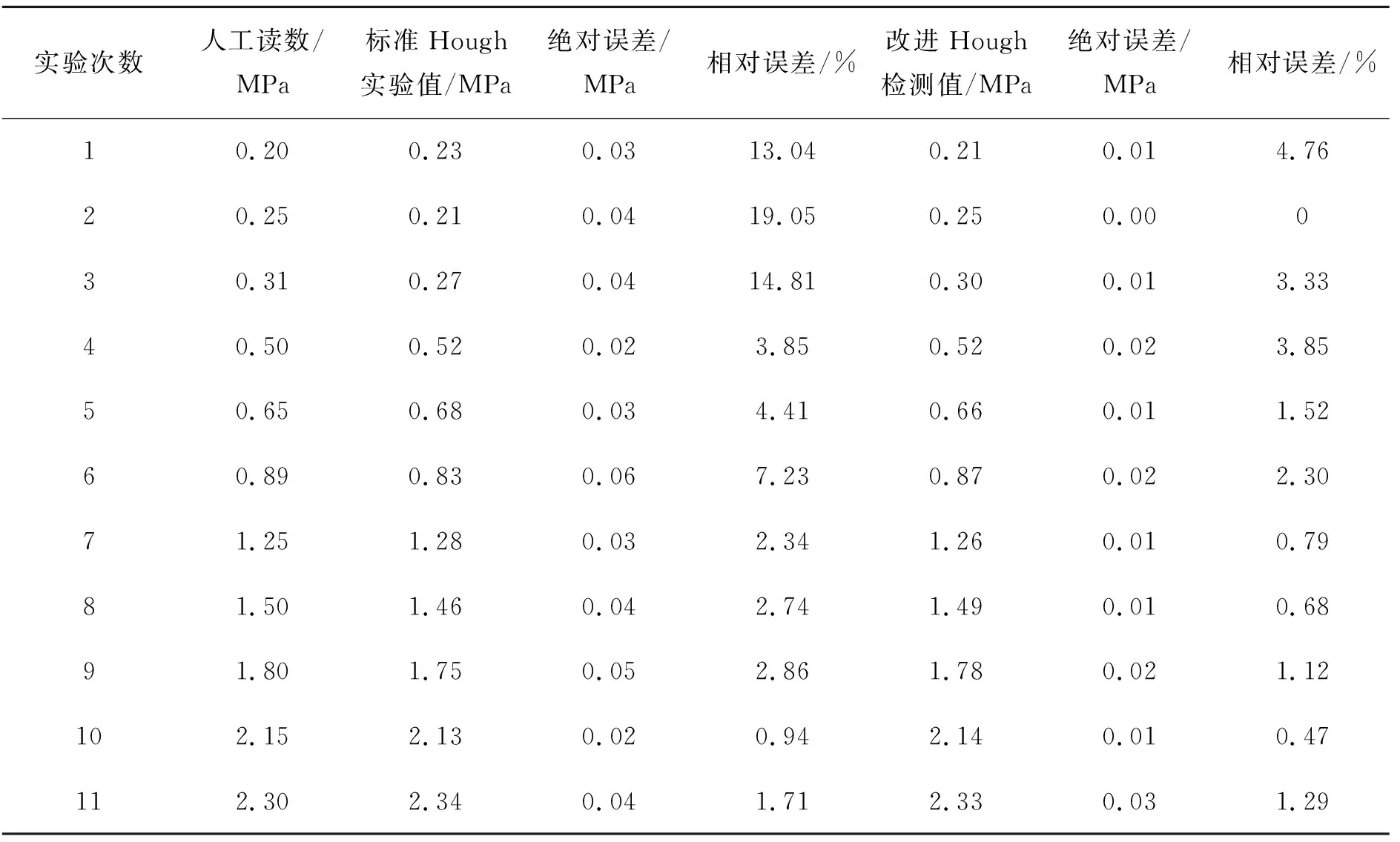
表1 仪表读数实验结果Tab.1 Meter reading experiment results

本文对于目标区域中心点的选取，结合圆心约束的Hough变换，保证了本文算法的实时性。本文算法与常用于指针式仪表识别的两种算法和文献[14]提出的算法进行了实时性比较，如表2所示。本文算法时间降低了大约29.41%，识别速度更快。

5 结 论

本文利用Otsu算法获取仪表指针二值图像和改进的Hough变换处理图像。Otsu自适应阈值分割仪表图像，放弃较小像素，通过对分割阈值的反复计算来分割出仅属于指针的像素。改进的Hough变换将分割出仅属于指针的图像分成若干行，提取每行前景区域的中心点，将中心点与表盘圆心共线进行表决统计。实验结果表明，本文算法比其他算法时间降低了大约29.41%，仪表读数误差最大为4.76%。改进算法减少了计算量，提高了检测速度，适用于在不同光照条件下对仪表进行均匀刻度识别，具有良好的实际应用前景。