基于学生化极差分布的随机森林变量选择研究

曹桃云,陈敏琼

(1.广东财经大学 统计与数学学院,广东 广州 510320;2.中山大学新华学院 经济与贸易学院,广东 广州 510520)

一、引 言

随机森林作为一种集成树算法,自Breiman于2001年提出就受到广泛研究[1]。如Zhang等人提出寻找最小随机森林,从树的预测率和树之间的相似性等,尝试在随机森林中找到最优子森林以解决black-box的问题[2]。Segal等人通过L2范数的不纯度度量,将随机森林推广至多元随机森林,使得分析数据的类型拓展到多元连续型的反馈变量[3]。Athey等人提出广义随机森林(Generalized Random Forests),通过局部估计方程给出相合估计并研究了估计的渐近正态性及建立有效的置信区间等,进一步完善了随机森林的理论基础[4]。由于随机森林的随机性:有放回的随机抽样和在选定候选分裂变量个数的条件下随机选取分裂变量,增强了集成树之间的独立性,缩小了泛化误差的上界,因此在预测能力上具有优势。如Chipman等人提出贝叶斯可加回归树,在进行药物发现实际数据的集成树算法预测能力比较中,随机森林表现最优[5]。同时随机森林算法内嵌的变量重要性度量为变量选择提供了依据,因此基于随机森林的变量选择也一直是统计机器学习研究的重要内容。如Robin等人将变量选择分为解释和预测两种目的,并提出两步算法达到不同的目的[6]。Hapfelmeier等人提出了基于置换检验的变量选择的理论框架且适用于任何的数据类型[7];Ishwaran等人提出基于分裂变量最大子树的最小深度重要性并给出了最小深度的概率分布,为变量的最小深度重要性度量奠定了理论基础[8]。目前基于随机森林进行回归问题变量选择研究中,绝大多数都是基于置换重要性度量,如冯盼峰等人提出两阶段变量选择:改进变量重要性排序,进行基于随机森林的逐步变量选择[9]。本文基于随机森林的最小深度重要性度量和置换重要性度量,提出一种变量选择新方法。通过引入学生化极差分布,在给定显著性水平下检验变量重要性得分是否具有差异性,根据检验结果将变量分组,对分组变量进行逐步回归挑选变量。运用数值模拟对新方法进行了分析验证,并在经典的波士顿房价数据上对新方法进行了实证研究。

二、学生化极差分布的随机森林变量选择

(一)学生化极差分布

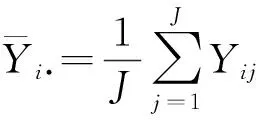
(1)

其中s是s2

(2)

的算术根,是未知参数σ2的样本估计量。

事实上,式(1)在μ1=…=μI=μ成立时,有下面的等式:

(3)

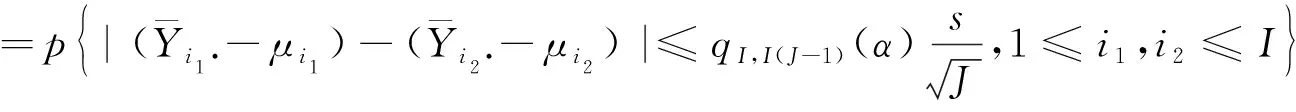
(4)

(二)基于随机森林的变量选择

给定样本S={Ym,Xm1,…,Xml},m=1,2,…,n,其中的连续型反馈变量Ym(∈R),特征变量Xv(为简洁,下文中出现的Xv均指特征变量Xv,v=1,2,…,l)。随机森林通过bootstrap方法有放回重抽样b次,b=1,2,…,B,得到独立同分布来自S的B个样本S1,…,SB。Sb(b=1,2,…,B)(为简洁,下文中出现的右下标或右上标b的取值均为b=1,2,…,B)中的样本称为袋内数据,袋内数据作为训练集递归拆分得到第b棵树Tb(为简洁,下文中出现的Tb均指第b棵树Tb),不在Sb的样本被称为袋外数据(OOB(b)),袋外数据作为测试集对Tb的预测结果进行评价。最小深度重要性和置换重要性的得分计算分别如下。

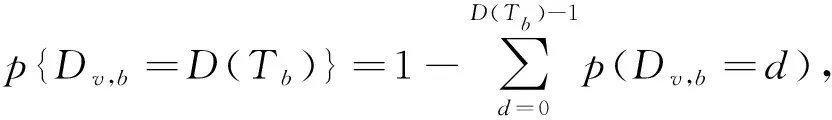
(5)

由式(5)可以看出,如果变量重要,则打乱后MSE增加,且增加的幅度越高,说明变量越重要。因此,置换重要性得分越大,变量越重要。

计算变量重要性得分后,新方法进行变量选择的具体步骤为:

①运行100次随机森林得到变量重要性得分均值,按照重要性从高到低降序排列;

②计算检验统计量SR,在给定显著性水平α下,对重要性得分进行差异性是否显著的检验;

③根据检验结果对变量进行分组,删除最后一组的变量,并比较删除前后100次随机森林的MSE,直至再删除就会增加MSE停止;

④将剩下的变量返回第①～③步,直至变量不满足删除条件停止;

⑤对现有变量返回第①步,给出重要性降序排列;

⑥对排序第一的变量做100次随机森林,计算MSE,赋值c1;

⑦接着把下一个变量加进来做100次随机森林,计算MSE,赋值c2;

⑧若c1

三、数值模拟和实证研究

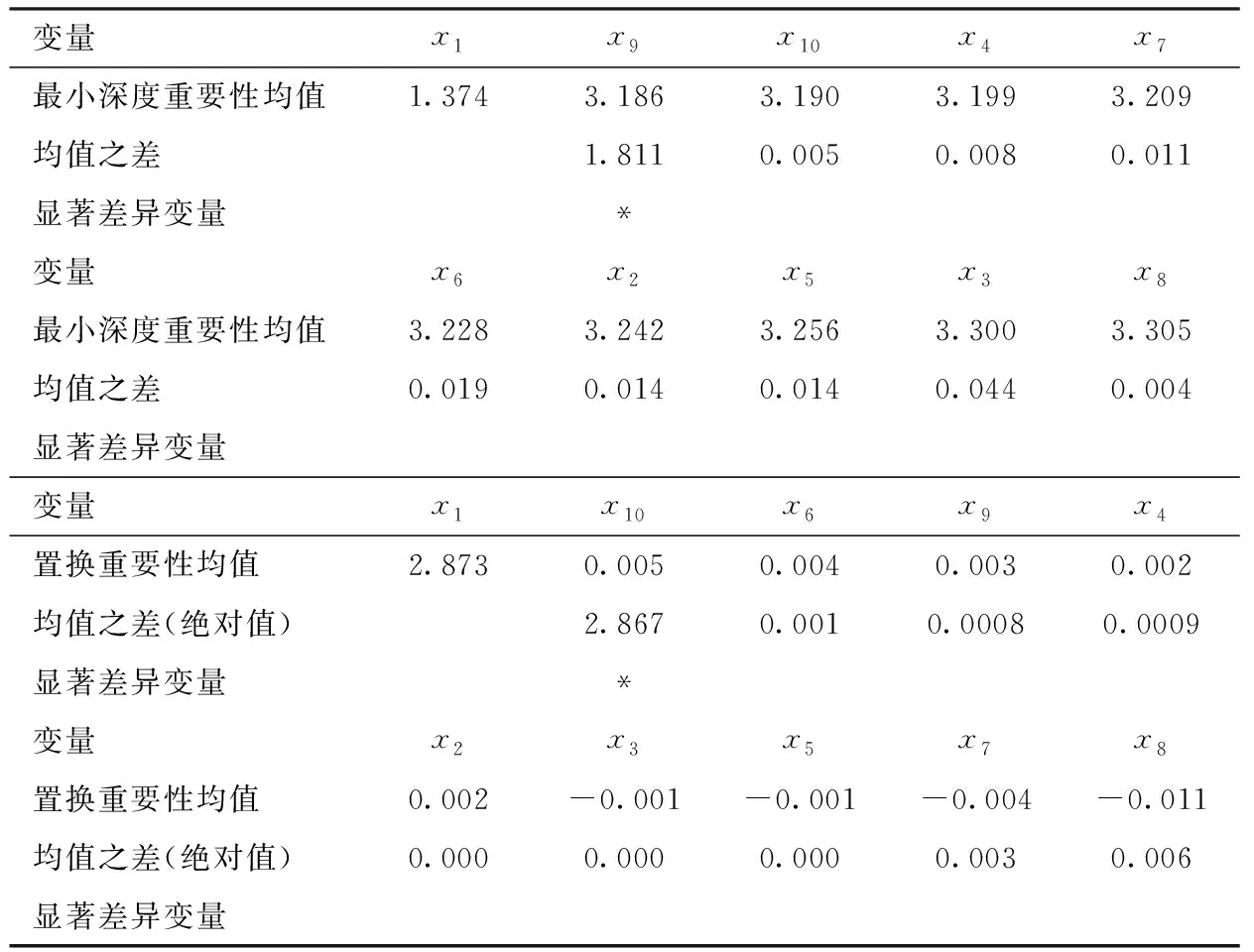
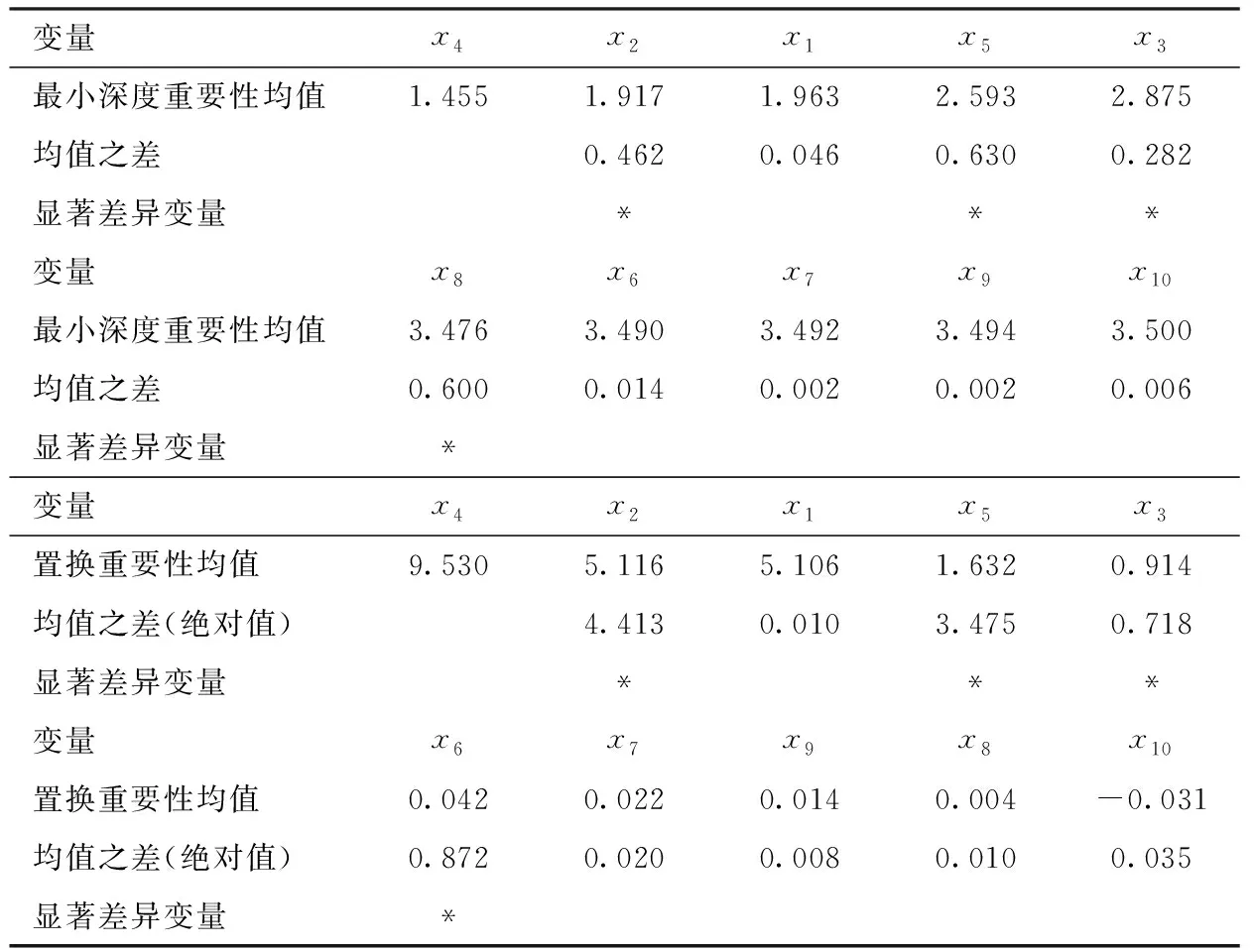
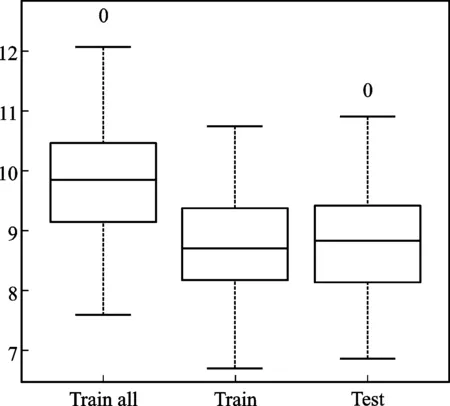
(一)数值模拟

为评估新方法的性能,设计了以下三个模型,每个模型的随机误差项ε均服从零均值且方差为σ2=1的正态分布。所有模拟均通过随机产生数据的方式进行了100次,每次模拟生成样本量n=200、特征变量个数l=10的独立均匀分布U(0,1)的数据。用其中50%的数据做训练集,剩余的50%做测试集,在训练集上生成随机森林得到特征变量的重要性得分,引入学生化极差分布进行差异性是否显著的检验,根据检验结果对变量进行分组,并按照逐步回归进行删除且比较删除前后的MSE,同时比较测试集运行100次随机森林的MSE。模拟是基于R软件包randomForest、randomForestExplainer并辅以部分编程实现,随机森林中的参数和最小深度重要性度量中的参数值均取缺省值。本文的显著性水平取α=0.05,下文出现的α和α=0.05不加以区分。模型如下所示。

模型一:y=5x1+5x2+ε,即y与x1,x2具有线性关系,x3,x4,…,x10是噪声变量;

模型二:y=5x12+ε,即y与x1具有二次函数关系,x2,x3,…,x10是噪声变量;

模型三:y=10sin(πx1x2)+20(x3-0.5)2+10x4+5x5+ε,即y与x1,x2,…,x5具有函数关系,是Friedman等提出的包含5个变量的回归函数,x6,x7,…,x10是噪声变量[11]。

值得注意的是表1、2、3、5的最小深度重要性临界值计算表达式中的s和置换重要性临界值计算表达式中的s是不同的。尽管都沿用相同的字母s,但是以不同的重要性得分:最小深度重要性得分、置换重要性得分,代入式(2)计算得到的s。为全文表达一致,符号尽可能精炼,在表1～3及表5的临界值说明中没有区分不同重要性得分的s。

从表1看出两种重要性都有唯一显著性差异的点,都出现在排名第二和第三的变量上。在最小深度重要性得分中,只有排名第二的x1和排名第三的x9的均值之差1.813大于临界值(0.114),意味着显著性水平为α时x1的重要性和x9的重要性具有显著性差异。重要性排名第一的x2和排名第二的x1的均值之差0.006小于临界值(0.114),即x1,x2的重要性差异是不显著的。排名第三的x9和后面7个变量依次均值之差小于临界值(0.114),即x9和后面7个变量的重要性差异是不显著的。于是把前两个变量x1,x2分为一组,把后面的8个变量分为一组。在置换重要性得分中,只有排名第二的x1和排名第三的x10的均值之差2.394大于临界值(0.115),意味着显著性水平为α时x1的重要性和x10的重要性具有显著性差异。重要性排名第一的x2和排名第二的x1的均值之差0.067小于临界值(0.115),即x1,x2的重要性差异是不显著的。排名第三的x10和后面7个变量依次均值之差小于临界值(0.115),即x10和后面7个变量的重要性差异是不显著的。于是把前两个变量x1,x2分为一组,把后面的8个变量分为一组。这样,两种重要性都是将10个变量分为两组,x1,x2的重要性处在第一组,x3,x4,…,x108个变量的重要性处在第二组,再对两组变量进行变量选择,如前所述步骤①～⑧,选出的变量为x1,x2。这个结果和模型一中的y与x1,x2具有线性关系,x3,x4,…,x10是噪声变量完全吻合。

表1 模型一的两种重要性均值降序列表及标出显著差异变量

图1展示了模型一数据中所有变量建模的100次随机森林的MSE(图1中最左边,用All标出)、训练集中选出前两个变量建模的100次随机森林的MSE(图1中间,用Train标出)、测试集中选出前两个变量建模的100次随机森林的MSE(图中最右边,用Test标出)的箱线图。可以看出两点,第一:训练集中选出前两个变量建模的100次随机森林的MSE较数据中所有变量建模的MSE有明显下降;第二:训练集中选出前两个变量建模的100次随机森林的MSE和在测试集中对选出的前两个变量建模的100次随机森林的MSE相差不大。由第一点反映出选择变量后模型的预测能力显著提高,由第二点反映出选择变量后随机森林模型预测能力的稳定性及随机森林中的OOB和测试集的等效性。

图1 模型一100次随机森林MSE对比箱线图

从表2可以看出两种重要性都有唯一显著性差异的点,且都出现在排名第一和第二的变量上。在最小深度重要性得分中,显著差异的点出现在排名第一的x1和第二的x9,由于排名第一的x1和第二的x9的均值之差1.811大于临界值(0.134),即在显著性水平α=0.05下x1的重要性和x9的重要性具有显著性差异。同样在置换重要性得分中,显著差异的点出现在排名第一的x1和第二的x10。两种重要性在排名第二到第十的变量重要性差异都是不显著的。因此,10个变量分为两组,x1的重要性处在第一组,而后面的x2,x3,…,x10的变量的重要性处在第二组。再对两组变量进行变量选择,如前所述步骤①～⑧,选出的变量为x1。这个结果和模型二中y只与x1具有二次函数关系,x2,x3,…,x10是噪声变量完全吻合。

表2 模型二的两种重要性均值降序列表及标出显著差异变量

图2展示了模型二数据中所有变量建模的100次随机森林的MSE(图2中最左边,用All标出)、训练集中选出第一个变量建模的100次随机森林的MSE(图2中间,用Train标出)、测试集中选出第一个变量建模的100次随机森林的MSE(图2中最右边,用Test标出)的箱线图。从图2可以看出训练集中选出第一个变量建模的100次随机森林的MSE较数据中所有变量建模的MSE略有下降,训练集中选出第一个变量建模的100次随机森林的MSE和在测试集中对选出的第一个变量建模的100次随机森林的MSE也略有区别。

图2 模型二100次随机森林MSE对比箱线图

从表3可以看出两种重要性具有显著差异的点都出现在排名第二、四、五和六的变量上,如最小深度重要性得分中,显著差异的点出现在排名第一的x4和第二的x2、排名第三的x1和第四的x5、排名第四的x5和第五的x3、排名第五的x3和第六的x8;置换重要性得分中,显著差异的点出现在排名第一的x4和第二的x2、排名第三的x1和第四的x5、排名第四的x5和第五的x3、排名第五的x3和排名第六的x6。反映了在α=0.05下,变量x4和x1,x2的重要性具有显著差异,变量x1,x2和x5的重要性具有显著差异,变量x5和x3的重要性具有显著差异,以及变量x3和x6,x7,…,x10的重要性具有显著差异。10个变量分为五组,x4的重要性处在第一组,x1,x2的重要性处在第二组,x5的重要性处在第三组,x3的重要性处在第四组,x6,x7,…,x10的重要性处在第五组,再对五组变量进行变量选择,如前所述步骤①～⑧,选出的变量为x1,x2,…,x5,这和模型三中的模型是5个变量x1,x2,…,x5的回归函数,x6,x7,…,x10是噪声变量完全吻合。注意到,在分成的五组中,最后一组的变量是噪声变量,前四组的变量都是模型中真正的变量,由于有线性函数x4和x5(系数不同)、二次函数x3、周期函数和交叉项x1,x2,使得这些变量重要性得分在学生化极差分布的检验中被区分,但x1,x2的重要性在一组,这个和模型三中x1,x2是交叉项且吻合。

表3 模型三的两种重要性均值降序列表及标出显著差异变量

图3展示了模型三数据中所有变量建模的100次随机森林的MSE(图3中最左边,用All标出)、训练集中选出前五个变量建模的100次随机森林的MSE(图3中间,用Train标出)、测试集中选出前五个变量建模的100次随机森林的MSE(图3中最右边,用Test标出)的箱线图。从图3可以看出训练集中选出前5个变量建模的100次随机森林的MSE较数据中所有变量建模的MSE有明显下降;训练集中选出前5个变量建模的100次随机森林的MSE和在测试集中对选出的前5个变量建模的100次随机森林的MSE相差不大。

图3 模型三100次随机森林MSE对比箱线图

从表1～3和图1～3可以看出,运用新方法在数值模拟三个模型中,都能够选出真正变量,如实反映模型。两阶段变量选择方法运用在三个模型中选出的变量和新方法完全一样[9]。

(二)实证研究

波士顿房价数据是回归分析中经典的数据,收集了波士顿不同城镇506个不同地区的居民住房信息,目的是探测波士顿房价及其影响因素。如Breiman等采用逐步回归选择重要变量并应用ACE(Alternating Conditional Expectation)方法确定变量的最佳变换形式,选出4个重要的特征变量[12],江勇杰增加了人均犯罪率作为环境因素进行自动选择可变系数的分位数回归等[13]。数据中住房价格中位数y和13个影响因素及变量类型范围等详见表4。

表4 波士顿房价数据中变量的详细列表

图4 Boston房价数据的两种重要性降序箱线图

表5 波士顿房价数据13个影响因素的两种变量重要性均值降序列表及标出显著差异变量

从表5可以看出运用新方法变量重要性降序分组为:x7,x11,x4,x8,x5,x9,x6-x1,x12-x2,x10,x13,x3,其中的x6-x1表示x6,x1的重要性差异不显著,从重要性角度视为一组(下文出现的符号“-”均表示此意);基于置换重要性的降序分组为:x7,x11,x8,x4,x5-x9,x6,x12-x1,x2-x10,x13-x3。按照步骤①～⑧进行变量选择,挑选出7个变量x7、x11、x4、x8、x5、x9、x12,两种重要性得分挑选出完全相同的变量。选出来的变量包含了Breiman等选出的4个特征变量x7、x11、x9、x12和江勇杰添加的x4这个特征变量[12-13]。同时注意到选出的另外2个变量x8,x5都是环境因素,如x8表示空气质量环境和x5表示交通便利环境。根据经济学原理,环境因素是影响房价的重要因素,在探测波士顿房价及其影响因素中选出来是合理的。实际上,运用冯盼峰等方法到波士顿房价数据中,选出的变量和新方法完全一致[9]。

四、结 论

本文以随机森林的最小深度重要性和置换重要性为基础,提出变量选择的新方法,通过引入学生化极差分布,在给定显著性水平下对变量重要性得分进行是否具有显著性差异的检验,根据检验结果分组,最后按照逐步回归进行选择。运用新方法在模拟设计的线性模型、二次函数模型和复杂模型上,都能够选出真正变量并在经典的波士顿房价数据中体现了实用性。

置换重要性是随机森林最常用的重要性度量,应当注意的是,最小深度重要性的度量可以得到更多详细信息,如最小深度的分布、根节点的分裂变量、分裂变量的次数、检验分裂变量是否服从二项分布的p值等,有助于更好地了解特征变量作出分析判断。实际上,两种重要性度量在非正态尤其是厚尾分布时有较大区别,最小深度重要性展现优势,已另文讨论。

两阶段变量选择方法运用在数值模拟和实际数据中,结果和新方法完全一样。两阶段变量选择方法适用于样本量小、维数高的数据,但其中变量分组如何确定并没有给出解释或标准化操作[9]。本文提出的新方法为变量分组提供了一种依据:基于最小深度重要性和置换重要性度量,引入学生化极差分布,检验变量重要性得分的差异是否显著,根据检验结果对变量进行分组。

新方法是在随机误差项服从正态分布的假设下,通过引入学生化极差分布,基于特征变量重要性得分进行显著性差异的检验。尽管有中心极限定理作保障,很多随机变量在大样本情形下都服从或近似服从正态分布,但是也有大量数据不满足正态分布,比如经济学、气象学等领域的数据。基于这种状况,是否可以考虑非参数检验以推广到更一般情形,这些也将是我们继续研究的内容。