周期分数阶傅里叶变换域多分量LFMCW 信号间的分辨研究*
张玉灵,李 坤,钱志升,朱健东
(1.郑州升达经贸管理学院,河南 郑州 451191;2.复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
0 引言
分数阶傅里叶变换(Fractional Fourier Transform,FRFT)作为傅里叶变换的一种广义形式,可以理解为线性调频(Linear Frequency Modulation,LFM)基分解,对LFM 信号具有良好的能量聚集性[1],非常适合于对其进行检测与参数估计。文献[2]基于Newton 法减少了FRFT 对LFM 信号检测和参数估计的计算量;文献[3]提出了一种基于分数阶功率谱的LFM 信号检测新因子;文献[4]对FRFT 域多分量LFM 信号的分辨问题进行了研究;文献[5]提出了一种分数阶域的交叠LFM 信号的分离方法;文献[6]讨论了分数阶域的滤波问题。FRFT 虽然对LFM 信号可以实现最佳的匹配检测,但是对针对线性调频连续波(Linear Frequency Modulated Continuous Wave,LFMCW)信号的检测却存在很多不足。在实际中接收机往往能够接收到多个周期的LFMCW 信号,但FRFT 对其处理增益仅局限在一个周期内,并且多个周期对应多个峰值也不利于信号的检测。为了解决上述问题,Geroleo 等人[7-8]在2010 年提出了周期Wigner-Hough 变换(Wigner-Hough Transform,WHT)算法,实现了WHT 对LFMCW 信号的最大似然检测,但由于是二次处理,计算复杂度高,不利于实时应用。借鉴其相关积累思想,朱健东[9]和黄宇[10]等人从FRFT 出发,于2013 年分别独立提出了周期分数阶傅里叶变换(Periodic Fractional Fourier Transform,PFRFT)的概念。该方法在保持与周期WHT 相当的检测性能的同时,利用FRFT 线性特性和快速算法大大降低了检测估计时的运算量。文献[11]进一步提出了一种基于PFRFT 的LFMCW 信号的自适应门限检测与参数估计方法。但是,针对PFRFT 域多分量LFMCW 信号的分辨和分离问题,现有文献没有开展进一步深入研究。当LFMCW 信号在PFRFT 域的尖峰相距较近无法分辨时,会导致目标信号被漏检。
本文首先从LFMCW 信号在PFRFT 域的频谱分布特征出发,对离散PFRFT 计算时单个LFMCW 信号的能量谱近似表达式进行了数学推导;其次根据多分量LFMCW 信号在离散PFRFT 域检测估计时的幅度叠加特性,研究它们在参数平面的分辨问题;最后研究了通过的量纲归一化因子的合理调整,提高在PFRFT 域分辨多分量信号的能力。
1 PFRFT 的定义
信号x(t)的PFRFT 定义式为[9]:
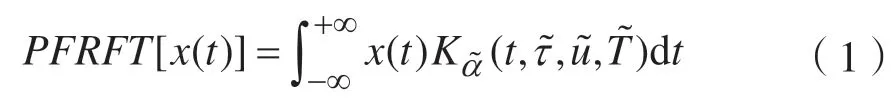
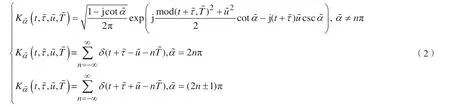
式中,mod(·)为取模算子,=pπ/2 为PFRFT 的旋转角度,p为PFRFT 的阶数,为任意实数。、分别表示时间偏移和调制周期搜索参数。PFRFT 核函数的参数集为,比传统的FRFT 参数和多了2 维和。
2 LFMCW 信号离散PFRFT 频谱
2.1 LFMCW 信号的PFRFT
单分量LFMCW 信号s(t)可表示为:
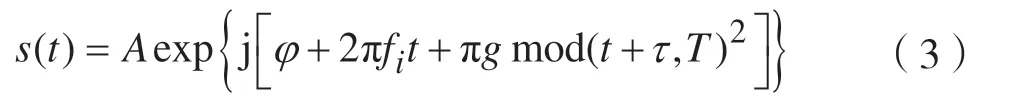
假设信号的初始频率和初始相位均为0,则信号形式如下所示:
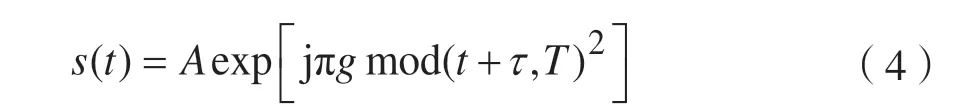
则信号的时频分布线与频率轴交于原点0。将信号表达式(1)代入PFRFT 变换表达式(4),可推导出信号的PFRFT 为:


式中:n为LFMCW 信号的周期数;T为周期。当T→+∞时,,说 明LFMCW 信号在一个周期内等效为LFM 信号,其最佳PFRFT 域的频谱服从sinc 函数分布。
2.2 LFMCW 信号周期分数阶谱的量纲归一化分析
Ozaktas 等人提出的快速离散FRFT 算法[12]精度高且计算复杂度低,因此得到广泛应用;而PFRFT 离散算法一般基于离散FRFT 算法来构造,从本质上讲,它们的量纲归一化相同。离散FRFT算法的量纲归一化基本原理如下:设s(t)在时间轴和频率轴上都是紧支撑的,时域区间和频域区间分别为[-Δt/2,Δt/2]和[-Δf/2,Δf/2],量纲归一化因子定义为s=(Δt/Δf)1/2,量纲归一化后新的坐标系为(x,v),量纲归一化后的坐标记为x=t/s,v=fs。
离散尺度化法和数据补零/截取法是两种实用化的量纲归一化方法[13]。本文采用前一种方法,过程为:令信号的时宽Δt=Td,信号的带宽Δf=fs,则s=(Td/fs)1/2。信号的时域和频域区间变为[-Δx/2,Δx/2],其中Δx=(Td fs)1/2,新的坐标系实现了量纲归一化,此时采样间隔变为1/Δx。
离散尺度化法量纲归一化会改变原有的LFMCW 信号的数字域参数值。LFMCW 信号s(t)经量纲归一化后的调频率、初始频率、最佳旋转角度和最大值的坐标分别为,则它们之间的量化关系式可以表示为:

根据文献[13],LFMCW 信号的实际参数值与归一化后的参数关系为:

联立上述两式可得峰值坐标与信号参数的关系式为:
从量纲归一化后的调频率、初始频率、最佳旋转角度和最大值坐标的关系式(7)可以看出,通过量纲归一化可以改变信号尖峰的坐标位置。归一化后,变换域中支撑区的宽度与中点坐标如下:

式中,n表示调频周期数。
2.3 信号离散PFRFT 的近似表示能量谱
对于连续信号s(t)如(4)式所示,从信号的PFRFT 推导值式(6)出发,取u~=0 时,可以得到s(t)的PFRFT 频谱最大值为:
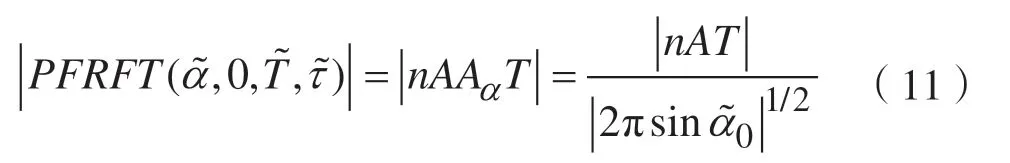
量纲归一化后,s(t)的PFRFT 频谱最大值[13]变为:

由式(12)和峰值坐标与信号参数的关系式(9)可知,量纲归一化还会改变信号频谱的最大值,其最大值为:


3 多分量LFMCW 信号的分辨能力
多分量LFMCW 信号模型为:

式中:Am为信号幅度;φm为随机初相;fm为初始频率;gm为调频率;Tm为调制周期;τm为时延;M为信号数目;Td表示观测时间。在PFRFT 域内,分辨多个能量相近、参数相近的LFMCW 信号,由于能量谱的叠加,会导致多个信号尖峰重叠无法分辨。

4 量纲归一化因子的选取
由量纲归一化后的调频率、初始频率、最佳旋转角度和最大值坐标的关系式(7)可知,在离散PFRFT 计算条件下,sr的尖峰与sl的尖峰在p轴上的距离为:
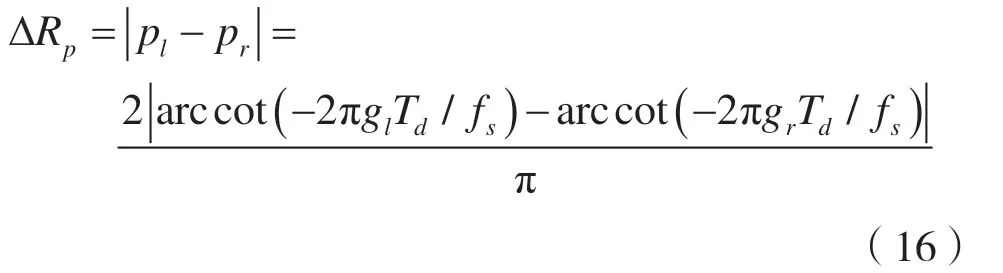
在轴上的距离为:
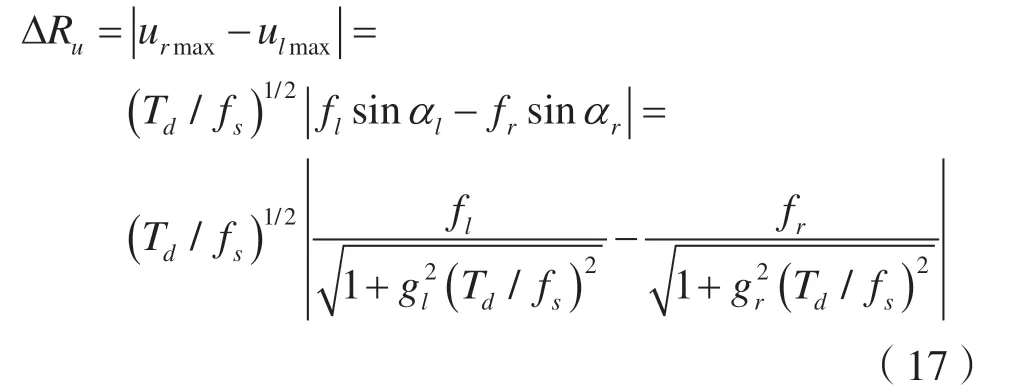
由式(16)、式(17)可知,两个尖峰的距离受归一化因子s影响。下面仿真分析两个信号尖峰之间的距离随s的变化关系。当fr=20 Hz、fl=22 Hz、gr=20 Hz/s 与gl=24 Hz/s 时,ΔRp与ΔRu随s=(Td/fs)1/2的变化曲线如图1 所示。

图1 两个信号尖峰在轴和p 轴上的距离随s 的变化
由图1 可知:
何东出的这档子事儿,让本来就心不甘情不愿去相亲的何西更有理了,他去找老爸商量,希望能找个理由把明天的相亲给推了,没想到老爸不买这帐。何西只好试着以理服爸:“爸,咱能与时俱进吗,二十一世纪都过去十年了,咱能不包办吗?”
(1)两个LFMCW 信号在轴和p轴上的尖峰距离与s取值有关,并且能在某个s处取得极大值;
(2)两个信号的尖峰在轴上的距离随s变化的动态范围比在p轴上的动态范围要大得多;
(3)两个信号尖峰在轴和p轴上的距离随着s的变化不能同时取得最大值。
在实际操作中,只要满足采样定理,就可以通过量纲归一化因子的合理选择,增大两个信号在参数(p,)平面上的距离ΔR,进而达到分辨两个信号的目的。当ΔR最大时,分辨能力达到最佳,即为:

因此当两个信号无法分辨时,可以选择一个合理的量纲归一化因子s=(Td/fs)1/2,尽可能地扩大ΔR,实现信号分辨。
仍以上述仿真数据为例,对信号幅度为的sr与sl,验证选择量纲归一化因子s=(Td/fs)1/2对信号的分辨效果。对前面的仿真数据:取Td=4 s,fs=1 000 Hz,调制周期数n=4 时,s=(Td/fs)1/2=0.063 2,两个信号在(T=1,τ=0)处的三维分布切片如图2 所示。当Td=4 s,fs=200 Hz,n=4 时,s=(Td/fs)1/2=0.141 4,两个信号在(T=1,τ=0)处的三维分布切片如图3 所示。
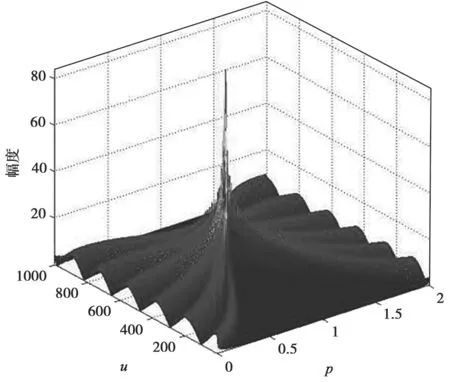
图2 s=0.063 2 时,信号的PFRFT 三维切片
比较图2 和图3 可以看出,在图2 中两个信号混杂在一起无法分辨,图3 中通过增大量纲归一化因子s使两个信号尖峰的距离增大,从而使两个信号得以分辨,也证明了图1 中距离变化曲线的合理性。由此可知,两个LFMCW 信号的临界分辨距离与信号的调频率、初始频率、观测时间、采样频率和调频周期数有关,同时受到量纲归一化因子的影响。由于接收信号的调频率、初始频率和调频周期数不受控制,而本文采取量纲归一化因子为s=(Td/fs)1/2,因此在不破坏信号采样定理的情况下,可以通过合理选择采样时间和采样频率,增大信号尖峰距离,提高PFRFT 对多个LFMCW 信号的分辨效果。

图3 s=0.141 4 信号的PFRFT 三维切片
5 结语
本文立足于LFMCW 信号在PFRFT 域的频谱分布特的分析,推导了LFMCW 信号在离散PFRFT 计算条件下的近似能量谱,研究了多分量LFMCW 信号在PFRFT 域的分辨问题。通过研究发现临界分辨距离与信号的调频率、初始频率、观测时间、采样频率和调频周期数以及量纲归一化因子有关。研究成果丰富了多分量LFMCW 检测估计分离理论。
——以匀加速直线运动公式为例

