一种基于强化Q 学习的跳频交会算法*

彭 艺，朱桢以，魏 翔，谢钊萍

（昆明理工大学，云南 昆明 650500）

0 引言

随着电磁环境的复杂化和用户数量的急剧增加，频谱资源的重要性日趋明显。大量无线频段被分配给专用设备，当专用设备不能充分利用授权频段且其他设备也没有适时接入授权频段时，往往造成频谱资源的浪费。传统跳频通信方法的效率较低，造成了大量频谱资源的浪费。针对授权的频段并没有被授权用户（Primary User，PU）充分利用的问题，文献[1]将认知无线电网络（Cognitive Radio Network，CRN）与跳频通信相结合，提出了利用未使用频谱的机会动态频谱分配（Dynamic Spectrum Access，DSA）技术，使次要用户（Secondary User，SU）以随机方式访问信道。文献[2]重点研究了共存状况下的SU 在占用相同PU 资源时的公平性问题，将SU 互相检测并建立一个公共的链路（Common Control Channel，CCC）的过程称为交会。交会是SU 间进行频谱管理、数据通信以及交换控制信息的重要操作。由于SU 间不能相互感知信息，在CRN 网络中实现交会是一个很有挑战性的难题。文献[3]提出了一种基于认知跳频网络的短交会跳频算法，经过公共控制链路实现有保证的短交会跳频算法，大大减少了交会时间。文献[4]引入了差分跳频系统，将差分跳频与拉丁方理论结合，利用拉丁方理论分配频率子集，实现了频率集的优化和动态分配，同时增强了跳频图案的随机性，增强了网络的抗干扰性能。

强化学习也称增强学习，是目前人工智能领域最热门的领域之一。2016 年，DeepMind 团队推出的AlphaGo在围棋对战中击败世界围棋冠军李世石，震惊世界。2017 年，进化后的AlphaGo 新版本，在乌镇举办的三番棋对战中3:0击败了世界第一柯洁。随后，DeepMind 团队又相继推出了AlphaGo Zero 等多个版本产品。强化学习源于对动物心理的模仿，类似于“蜜蜂辨色”和“小鸟啄食”的试错机制，经过与环境的交互，改变行为状态并映射出不同行为，从而获得最大化回报。

随着人工智能的发展，数据驱动、驱动的机器学习方法能高效解决各类问题[5]。作为机器学习领域的重要分支，强化学习能避免大量重复的计算，从样本数据中准确提取所需特征数据，在满足个性化、具体化要求的同时，节约了大量重复计算的成本。强化学习的核心思想是将学习视作马尔可夫决策（Markov Decision Process，MDP）的测试过程[6]，其智能系统由策略、回报函数、值函数3 个单元中的一个或多个组成，强化学习基本过程见图1。

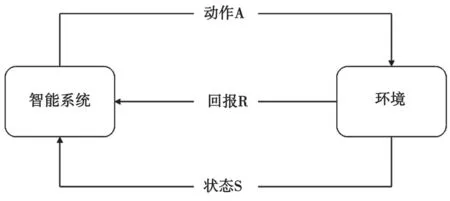
图1 强化学习基本过程

Q 学习也称为离轨策略TD 学习，是强化学习的一个重要分支，也是极具代表性的强化学习算法。作为一种无模型的强化学习方法，Q 学习不需要确知状态转移概率和即时回报，因此在进行迭代更新时，智能系统要遍历每一个状态动行为对[7]的值。

在CRN 的基础上，本文提出一种基于强化Q学习的跳频交会算法，利用强化学习的相关算法对交会过程进行预测，选择最合适的交会路径，实现有保证的快速交会，同时缩短交会时间。文中所提强化Q 学习算法具有提供有保证的交会、大幅缩短交会时间和适用于对称与非对称的模型的特点。

1 系统模型

提出一个CRN 网络场景，在一个区域内有多个PU 和N个SU 共存。为每个SU 配置一个认知无线电装置，假设每个次级用户都存在唯一的ID，且能感知到区域内其他用户的ID，同时US 用集合S={s1,s2,…,sN}表示。将某个授权频段（Licensed Spectrum）分成M个不重叠信道C={c1,c2,…,cM}。假设每个信道有唯一的索引且无线用户移动的速度缓慢，彼此之间无干扰，通过一个信道索引向量v={an}把Nc个信道分配给PU，将PU 在时刻t的信道行为状态定义为，其中表示在信道n上的传输概率。因为此时信道仅有可用和不可用两种状态，所以∈{0,1}，且n={1,…,Nc}。用ci表示第i个信道，将系统时间等分为相等的时隙t。当用户i能使用完成跳频且不干扰主要用户PU的正常通信时，称cpi为用户i的可用信道。在CRN 中，每位用户对应的可用信道集是不同的。表示第i个用户的可用信道集中有p个可用信道。例如，用sa、sb表示次级用户a和用户b，假设每个用户能够同时接入多个信道并占用它们，用户a的可用信道集为，用户b的可用信道集为，且Fa,Fb∈C。由于可用信道是动态变化的，假设无线设备发射功率恒定，信道变化缓慢，Fa与Fb通常不全相同。用G表示两个用户的共同信道，即Fa∩Fb=G。

将多个用户在同一时隙内跳频到公共信道的过程称为交会，实现交会的必要条件是Fa∩Fb≠∅，即|G|≠0。将跳频通信系统的时隙划分成长度相等的时隙，以时隙作为认知跳频的单位。假设文中的时隙差为整数。本文研究的重点是将Q 学习的过程运用到跳频算法中，为用户生成跳频序列，保证有限跳数的跳频交会，得到更短的交会时间。

系统中，假设每个时隙的传输时间T和接收时间R都相等。每个时隙中，CR 节点将从其信道列表中选择一个信道并尝试一次交会。为了提高效率，时隙必须足够发送和接收消息。当没有数据传输时，允许节点关闭收发器，同时保证网络中的时间同步。时隙模型如图2 所示。

图2 时隙模型

图3 从时间角度描述了交会过程。t=1 时，节点A 和节点B 都在信道1 上，处于彼此的通信范围内。节点A 和B 在信道1 的t=1 时刻相互通信，以保证节点的时间同步，并尝试与其他节点交会。在时间t=2 时，当节点A 尝试在信道2 上交会时，节点B 保持。同样，在时刻t=3 时，节点B 尝试在3点交会，节点A 现在保持它的尝试。节点B 和节点C 在信道4 的t=5 处交会，之后3 个节点实现交会，并遵循相同的规律与其他节点交会。

图3 交会模型

通过定义集合设计信道跳频调度：

式中：d取整数；Fa∩Fb≠∅。

在跳频通信中，假设两个用户分别为发送端和接收端，且只考虑可用信道生成的跳频序列，包含所有可用信道的集合C={c1,c2,…,cM}。

1.1 发送端序列

假设发送端用户a包含可用信道集Fa=C={c1,c2,…,cM}，构造发送端序列sa={c1,c2,…,cM,cM,cM-1,…,c2,c1,c1,c2,…}。由于发送端序列由c1重复到cM，推导出序列的周期T=2M-1，其中M为信道总数。

用t表示时隙，发送端序列可表示为：

式中，k为整数。

1.2 接收端序列

假设接收端用户b包含全体可用信道，则Fb=C={c1,c2,…,cM}，构造接收端序列sb={c1,c1,…,c1,c2,c2,…,c2,cM,cM,…cM,c1,c1,…}。为了说明信道交会的过程，以信道集合C={1,2,3}为例，信道数M=3，跳频周期T=5，用户a在t=0 时隙开始跳频，用户b在t=1 时隙跳频，且用户b每隔T=5 完成一次跳频，如图4 所示。

图4 周期序列交会过程

由于各个用户开始跳频的时间通常不同，因此将用户a和用户b对应的sa序列和sb序列表示为Sa(t+d)和Sb(t)，即用户b开始跳频的时间滞后于用户a开始跳频时间的d个时隙，由此能够表达出最大交会时间MTTR：

期望交会时间ETTR为：

一般地，如果序列满足周期T，那么序列总会在T个时隙后重复相同的值，因此一定满足S(t)=S(t+kT)，其中k取整数。对于本文序列，当信道对于用户都可用时，序列的周期为M(2M-1)。

2 Q 学习

2.1 Q 学习相关理论

将Q 学习与认知跳频相结合，能提高系统的智能化和高效化。Q 学习是一种无模型强化学习，通过与环境的交互来学习最优策略。Q 学习中的主要元素通过四元组表示。其中：S为环境状态的有限集合；a为Agent 动作的有限集合；P:S×A×S→[0,1]为状态转移概率函数，P:S×A×S→R为反映学习目标的回报函数。

假设CRN 中的每个SU 都能独自做出信道跳频的决策，通过将SU 的Q 学习模型转化为根据历史状态和当前动作的联合效用，以决定跳频信道选择的方式。根据Q 学习算法，结合认知跳频的具体场景，定义其中的状态、动作、回报和SU 的学习策略。

（1）状态（State）：在仅有1 个主要用户和2 个次要用户的场景中，定义SU 当前所在信道的状态=∈S，这里的S={sk}表示有限状态空间sk={0,1}。在信道跳频的状态中，仅有跳频或者等待两个随机事件，当其中之一发生时，状态自转移至下一状态。

（4）策略（Policy）：在强化Q 学习中，所谓学习，就是通过学习先前状态中的动作及收益，映射并迭代出当前的动作选择，其中从状态到行为的映射被称为策略，用π表示。

2.2 QLCH 算法

根据相关理论，提出了一种Q-学习跳频算法（Q-Learning Channel-Hopping，QLCH）。在一个认知跳频场景中，PU 对于授权频段有最高的占用优先级，SU 通过感知频谱空洞机会性地接入授权频段，以提高频谱利用率。QLCH 算法将SU 的跳频序列分成两类，一类是发送端跳频序列，另一类是接收端跳频序列。正常情况下，SU 都以接收端序列周期跳频。当SU 有信息需要发送时，转为发送端序列跳频，通过与接收端序列的交会，实现SU 之间的数据通信和信息交换。交会完成后，转为以接收端序列跳频。

两类序列的生成步骤如下。

当SU 不进行交会时，以接收端序列周期跳频。通过感知环境中的可用信道，生成长度为的接收端序列，将序列按递增的自然数排列为={1,2,3,…,p}，SU 按照p为周期进行接收端跳频。

当SU 发送信息时，采用发送端序列跳频。发送端序列没有固定的模式，根据QLCH 算法训练生成。

定义策略π:S→A。在Agenti与环境交互时，Agenti感知当前状态∈S，并根据策略π选择动作∈A，最终使环境转换到新的状态∈S并向Agenti反馈回报。将此过程不断重复，直至获得最优策略π的过程即学习的过程。

策略π下的状态值为：

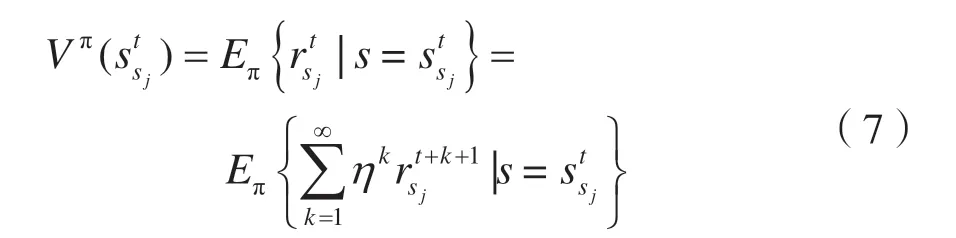
式中：Vπ(s)表示预期的贴现奖励；η∈(0,1)表示折扣因子。经过重复学习，从一段时间内的最大化累积回报值中获得最优动作∈A。

根据贝尔曼最优化准则，一个独立设置的环境中至少有一个最优策略，表示为：

Q值是策略π在状态下采取行动的期望回报，表示为：

重复此过程，根据Robbins-Monro 理论，Q值在最优策略下收敛到最优，表示为：

重复迭代式（5），实现状态动作值函数的优化，可以得出：

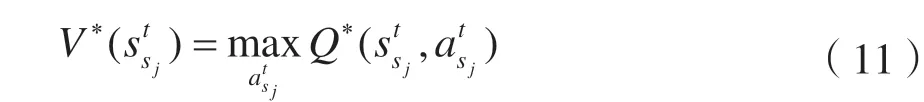
根据相关理论，定义Q函数为：

式中：φsj表示sj下的折扣因子，表示未来收益在当下的值，φsj∈[0,1]，φsj越接近1 时，表示未来的动作在总的行为动作值中占据越多的主导值，反之，则表示未来的动作对当下的影响很小；Φsj表示学习速率，是一个恒定的步长参数，取值范围Φsj∈(0,1)，Φsj取值越接近1，表示学习速率越快，收益会立即作出响应。

在最优策略下，Q 学习算法进行迭代更新，将更新的数值保存为一个Q值表。经过多次重复迭代后，它逐渐逼近拥有最大期望收益的动作值：

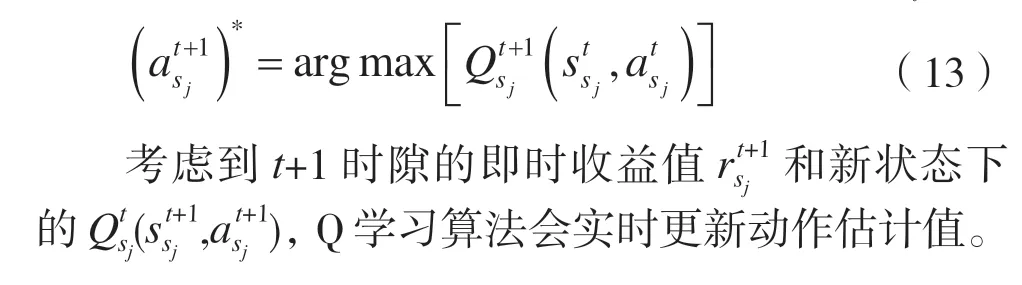
2.3 Q 算法收敛性证明

因为Q 算法是一个随机过程，可通过随机逼近技术近似。假设提出的Q 算法具有时变学习速率Φsj，根据Robbins-Monro[8]理论得出以下定理。

定理 满足以下4 个条件：

（4）若折扣因子φsj=1，所有策略以概率1 趋向于自由状态。

证明：

考虑一个多元收益模型，回报值组成有限元素数量的集合，取{-5,5}。不难看出，集合元素的方差是有限的，符合条件（2）。

在任意时隙t下，假设Φsj=Φ<1，任取一个较小的Φ值，假设选取0.01，必然满足两个条件。

当φsj=1 时，在增益最大化策略指导下的无限水平模型趋向于实现长期平均收益最大化的目标，此时所有策略都被引向概率为1 的自由状态，满足条件（4）。

定理得证。

3 实验仿真

为验证算法性能，将对称和非对称情形进行对比。选择EJS[9]、AHW[10]和FRCH[11]这3 种具有代表性的算法与QLCH 算法进行仿真。假设认知网络中的信道总数M为40，SU 能检测其中的20 个。

在非对称情形中，用户a的可用信道集，用户b的可用信道集，p和q分别为用户a和用户b的可用信道数。根据理论推导，非对称情形下跳频序列的最大交会时间为q(2M-1)。当所有信道对用户a可用且只有一个信道对用户b可用时，最大交会时间取最大值M(2M-1)。随着可用公共信道的增加，当时，满足对称模型的情形。保证SU 的跳频开始时间随机，以2 为单位增加SU 之间的共同信道数G，取100 次随机运行的平均值作为平均交会时间。

如图5 所示，在非对称情形时，伴随着共同信道的增加，所有算法的平均交会时间都呈现下降趋势。开始时，AHW 和EJS 算法的平均交会时间较高，最终下降到150～200 ms；FRCH 以及QLCH 算法随着共同信道数G的增加保持在较低水平；公共信道数G较少时，QLCH 算法平均交会时间略低；随着G的增加，两种算法的性能相近，但是FRCH 算法不能实现有保证的交会，QLCH 算法在非对称情形能够保证最长为M(2M-1)个时隙的交会。在对称情形下，FRCH 和QLCH 算法的平均交会时间都很低，但QLCH 能保证2M-1 个时隙的交会，且随着训练的增加，交会时隙逐渐缩短。

图5 算法的平均交会时间

为了进一步研究对称情形下的算法性能，图6和图7 将4 种算法的期望交会时间和平均交会时间进行对比，同时比较理论结果与仿真结果。QLCH算法在对称情形下的期望交会时间和最大交会时间都较低，且仿真结果和理论计算结果非常接近，说明算法具有较强的稳定性。

图6 不同算法的期望交会时间

图7 不同算法的最大交会时间

4 结语

本文研究了基于强化Q 学习的认知无线网络的跳频交会问题，针对两个SU 对算法进行了评估。提出的QLCH 算法在对称和非对称模型下，分别保证了周期为2M-1 和M(2M-1)的交会。仿真结果显示，QLCH 算法在对称模型下性能与FRCH 算法相近，且能实现周期为2M-1 有保证的交会，在非对称模型下的性能显著优于传统算法。综上，QLCH算法不仅实现了有保证的跳频交会，而且比现有方法具有更小的交会时间。