机载雷达天线伺服控制扰动观测器建模仿真

赵熹，李启蒙

（1.陕西国防工业职业技术学院 智能制造学院，西安710300）

（2.陕西国防工业职业技术学院 电子信息学院，西安710300）

0 引 言

雷达系统对目标的搜索、识别和探测，在目标精确定位、精确制导攻击、光电体系对抗等应用场景中起到重要的作用。它为信息的获取与态势感知、进行指挥决策提供依据，其总体技术指标与收发光学子系统、信号处理子系统、伺服控制系统密切相关。雷达天线伺服控制是实现雷达天线快速响应、大范围扫描和空间精确定位定向的控制系统，是雷达系统进行精确跟踪和定位的前提，已被广泛应用于陆海空不同领域的平台中。随着伺服控制技术、电机及驱动技术、传感器技术、精密传动技术和振噪控制技术的发展，雷达天线伺服控制的性能也在提升。

雷达天线伺服控制（ARASC）能够实现雷达天线按照设定的速度、范围、扫描算法对一定空域进行周期性的扫描、探测，以感知外部态势和获取目标信息。甄洪涛等、徐鑫、王福增等、周立新等和凡国龙等分别通过模糊自适应控制器、自适应控制、运动控制补偿算法、仰角抖动控制和自抗扰控制技术等控制方法对雷达天线伺服控制系统进行了建模仿真等研究；吕向阳、范大伟等和夏鑫等分别对雷达天线电子稳定方程应用、定位精度诊断和车载平台自动调平控制进行了研究；冯良祥等、朱浩等和王育东等分别对雷达天线座齿轮传动间隙对伺服控制的稳定性、转速的影响，负载转矩及惯量匹配、载体姿态变化对雷达天线波束指向精度的影响等进行了建模仿真；Ji Haiyu等通过神经滑模变结构控制克服舰载摆动对雷达伺服系统的影响，仿真试验证明其能够更好地用于雷达伺服系统对机动目标的稳定跟踪；Zuo Zhiqiang等运用自抗扰控制估计和补偿天线伺服系统模型不确定和有限实时干扰，通过仿真与试验证明自抗扰控制对天线伺服系统的有效性；余驰针对载体姿态变化对机载光电转塔系统视轴引起的不稳定，通过陀螺稳定、方位和俯仰两自由度联合建模仿真，运用经典三闭环PID控制对不同模拟姿态扰动进行仿真分析。上述文献从不同角度对雷达天线伺服控制精度、稳定性、动力学特性和陀螺稳定控制等方面进行了研究，而对于环境影响下的雷达天线伺服控制的研究鲜少涉及。实际应用中，由于雷达天线结构尺寸较大，连续360°扫描运动和载体快速的机动，雷达天线受到迎风阻力和载体运动相对气流作用力，会对其产生周期性的空气阻力扰动，等效转换则会给方位扫描运动带来扰动力矩，给雷达天线扫描空域目标和搜索探测带来负面影响。

本文以雷达天线伺服控制扫描运动过程为研究对象，建立机载雷达天线伺服控制的动力学模型、伺服控制模型，并对扰动观测器进行建模和设计，通过扰动观测器将附加扰动引入到被控对象的控制输入端进行补偿；对不同风速下雷达天线伺服控制进行建模仿真和试验分析，以期为机载雷达天线伺服控制稳定扫描、精度提高和工程应用提供技术支持。

1 雷达天线伺服控制系统的动力学模型

雷达天线伺服控制系统的动力学模型如图1所示。

图1 机载雷达天线伺服控制系统的动力学分析Fig.1 Dynamic analysis of ARASC system

雷达天线固定于俯仰框（即P框），俯仰电机接受控制器的指令，通过俯仰电机驱动直线作动器，使俯仰框可绕

y

轴旋转运动，在0°或90°两者之间切换，实现收起和放下。雷达天线放下后，方位框（即Y框）及连接于其上的俯仰框和俯仰框上的雷达天线，通过方位电机驱动减速器，使方位框可绕

z

轴360°旋转运动，实现对一定空域的搜索警戒。假设雷达天线在放下状态受到的空气阻力为

F

，则有：

式中：

C

为空气阻力系数；

ρ

为当地空气的密度；

S

为雷达天线迎风面积；

v

为雷达天线与空气气流的相对运动速度。为了简化研究，假设雷达天线承载平台的运动速度为

v

且载体航姿保持稳定不变，雷达天线放下后的初始运动零位与航向垂直，某时刻雷达天线伺服运动的角度为

θ

，风速为

v

，风向为航向负向，且风速在短时间内在某一区域稳定不变。当

t

时刻雷达天线方位伺服运行到与航向夹角为

θ

时，

ω

为雷达天线方位伺服运动的角速度，则：

设雷达天线方位运动的回转半径为

r

，方位输出端回转的摩擦系数为

u

，则雷达天线方位伺服运动扫描时，空气阻力产生的附加扰动转矩

T

为

以某型机载雷达天线为例，设飞机飞行速度为216 km/h，风速分别为10和20 m/s，雷达天线方位伺服运动速度为30（°）/s，可得雷达天线受到的空气阻力及产生的附加扰动转矩如图2~图3所示。

图2 空气阻力曲线Fig.2 Curve of air resistance

图3 空气阻力产生的附加转矩曲线Fig.3 Additive torque curve by air resistance

2 雷达天线伺服控制模型

机载雷达天线伺服控制系统能够通过俯仰运动实现雷达天线的收起和放下运动。放下时通过方位自由度360°扫描运动，对一定空域目标进行搜索、识别和探测，从而进行侦查、警戒和态势感知，为指挥控制和决策提供支持。俯仰和方位的伺服运动控制多采用直流永磁无刷电机通过减速传动环节来实现收放功能和方位360°扫描运动。直流永磁无刷电机在同等条件约束下具有转速高、矩频特性随转速变化波动小、运行平稳、寿命高、温度变化影响小、功率密度高和伺服性能好的优点，已经广泛应用在雷达天线伺服控制。对于直流永磁无刷电机，其电压平衡方程、电磁转矩方程和反电动势方程可表示为

式中：

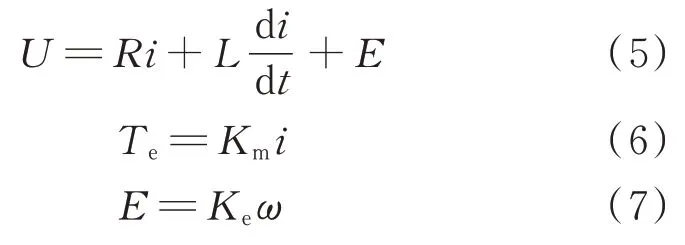
U，i，R，L，E

分别为直流永磁无刷电机电枢两端的电压，电枢绕组的电流，电枢绕组电阻，电枢电感和电枢反电动势；

T

为电机电磁转矩；

K

为转矩系数；

K

为反电动势系数；

ω

为电机转子的角速度。

直流永磁无刷电机主要参数：额定电压28 V，额定转速4 200 r/min，额定转矩3.4 N·m，额定功率1.5 kW，绕组电阻0.147Ω，绕组电感0.21 mH，转 动 惯 量0.86×10kg⋅m²，转 矩 系 数0.063 N·m/A，反电动势系数0.105 V·s/rad。

雷达天线方位伺服运动平衡方程为

式中：

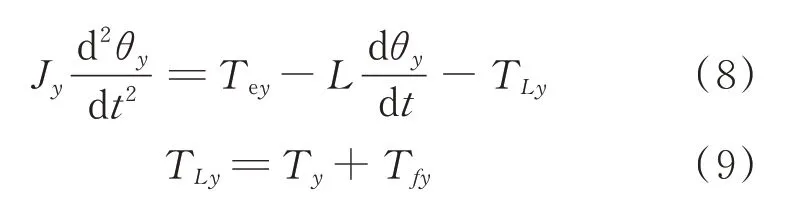
J

为折合到方位电机轴的转动惯量；

θ

为方位电机轴的转动角度；

T

为方位电机电磁转矩；

T

为方位负载转矩；

T

为摩擦转矩。对式（5）~式（9）进行拉氏变换，整理可得方位电机电枢电压和电机输出角速度之间的传递函数

G

（

s

），即：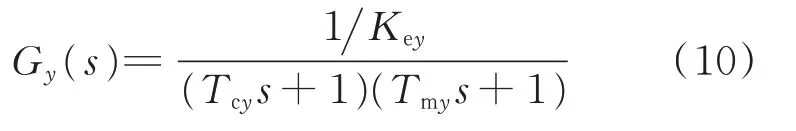

式中：

T

=

L

/

R

，为电磁时间常数；

T

=

JR

/

K

K

，为机电时间常数。

3 扰动观测器的设计

雷达天线结构尺寸较大，在载体运动、风速、风向和雷达天线伺服运动扫描角度变化的作用下，会承受周期性的扰动干扰，对雷达天线伺服运动扫描的稳定性和精度产生不利影响。因此，本文在雷达天线伺服运动控制系统中提出基于扰动观测器（DOB）补偿扰动的控制架构。扰动观测器的补偿思路是把被控系统的输出与参考模型输出的差异作为一个等效的干扰，通过扰动观测器估计该等效干扰，将其作为一个补偿信号送至被控对象的输入端，以消除实际扰动对被控系统性能的影响。扰动观测器的补偿扰动框图如图4所示，

D

（

s

）为实际被控对象模型，

D

（

s

）为被控对象模型的逆，

u

和

y

分别为输入和输出，

d

为受到的扰动，

W

（

s

）为设计控制器的传递函数，

d

为扰动

d

的估计值，将其送至前向通道即可抵消实际的扰动。

图4 扰动观测器的补偿框图Fig.4 Compensation block diagram of DOB

实际系统应用时，由于被控对象

D

（

s

）的参数是变化的，在控制器中只能采用其标称模型

D

（

s

）。又因

D

（

s

）是严格的真有理分式，

D

（

s

）在实际中难于实现，故通过被控对象标称模型的逆

D

（

s

）取代实际 被 控对象模型 的 逆

D

（

s

）。同时增加一个低通滤波器，保证

Q

（

s

）

D

（

s

）扰动观测器的物理实现性，改进的扰动观测器一般性结构框图如图5所示。

图5 扰动观测器的一般性结构框图Fig.5 General structure diagram of DOB

扰动观测器设计的核心是低通滤波器

Q

（

s

）的设计，以满足

Q

（

s

）

D

（

s

）为有理分式。

Q

（

s

）的带宽大于系统带宽可使得系统稳定性得到保证，

Q

（

s

）的带宽小于噪声带宽能够避免对噪声的放大，因此

Q

（

s

）的带宽需要综合考虑稳定性和噪声抑制能力。

N

阶

Q

（

s

）可设计为

式中：

N

为

Q

（

s

）的阶数；

M

为

Q

（

s

）与

D

（

s

）的相对阶数；

τ

为

Q

（

s

）的截止频率。

τ

大则带宽小，噪声抑制能力强；反之，

τ

小则带宽大，抗干扰能力强，噪声抑制能力弱。

Q

（

s

）阶次选择越高，噪声抑制效果越好，但同时也会使得扰动观测器的实现变得更加复杂。机载雷达天线伺服控制需要稳定扫描且具有良好的抗噪声能力，因此

Q

（

s

）设计为

4 仿真与分析

4.1 系统仿真

基于扰动观测器的机载雷达天线伺服控制的原理图如图6所示，

W

（

s

）、

W

（

s

）、

W

（

s

）分别为位置调节器、速度调节器和电流调节器；Dy‐namic model是按照雷达天线伺服控制系统的式（1）~式（4）建立的动力学模型；

θ

为位置信号输入。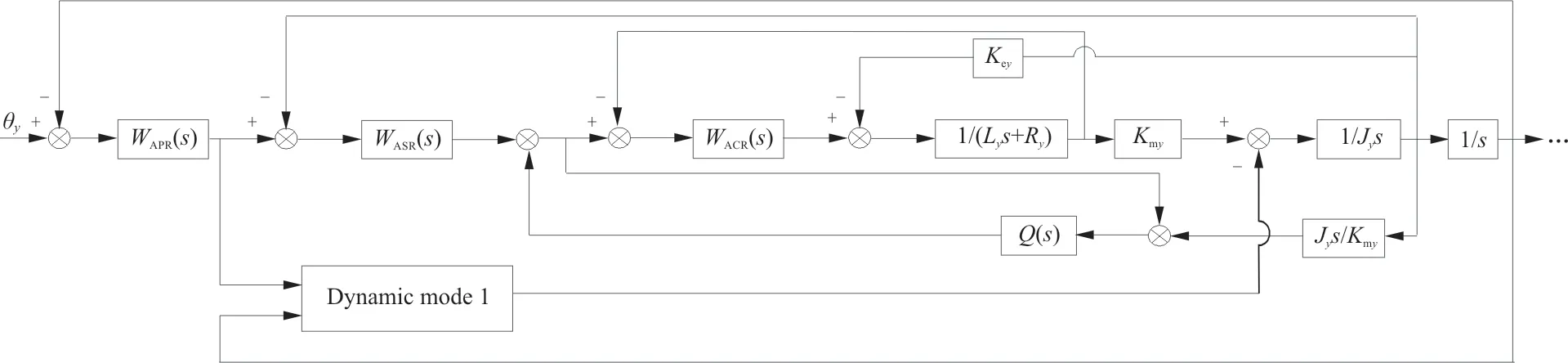

图6 机载雷达天线伺服控制扰动观测器框图Fig.6 ARASC diagram with disturbance observer

在MATLAB/SIMULINK仿真环境下，通过已经建立的雷达天线的动力学模型、雷达天线伺服控制模型和扰动观测器模型，配置位置环参数

K

=150、

K

=4 800；速度环参数

K

=12、

K

=0.5；电 流 环 参 数

K

=400、

K

=0.6、

K

=3。DOB中

τ

=0.002 5，设定仿真参数，采用变步长四阶龙格库塔法。在不同扰动条件下，雷达天线伺服控制在经典三闭环控制和基于扰动观测器的控制下的仿真特性如下：

（1）在雷达天线按照设定的30（°）/s扫描指令输入下，载机以60 m/s飞行，受到的风速为10 m/s。经典三闭环控制和基于扰动观测器的雷达天线伺服控制的误差和速度仿真试验特性如图7~图8所示。

图7 误差仿真曲线Ⅰ（V w=10 m/s）Fig.7 CurveⅠof error simulation（V w=10 m/s）

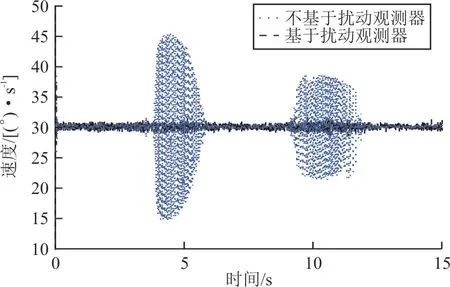
图8 速度仿真曲线Ⅰ（V w=10 m/s）Fig.8 CurveⅠof speed simulation（V w=10 m/s）

（2）在雷达天线按照设定的30（°）/s扫描指令输入下，载机以60 m/s飞行，受到的风速为20 m/s。经典三闭环控制和基于扰动观测器的雷达天线伺服控制的误差和速度仿真试验特性如图9~图10所示。

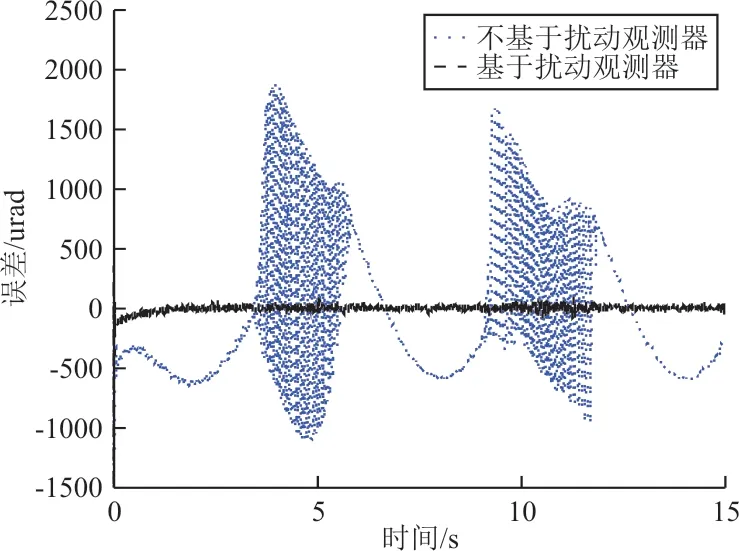
图9 误差仿真曲线Ⅱ（V w=20 m/s）Fig.9 CurveⅡof error simulation（V w=20 m/s）

图10 速度仿真曲线Ⅱ（V w=20 m/s）Fig.10 CurveⅡof speed simulation（V w=20 m/s）

4.2 仿真结果分析

从图7~图8可以看出：当风速为10 m/s时，雷达天线同时受到载机运动相对气流和迎风阻力的作用，在雷达天线上产生附加扰动转矩，转矩的大小随着方位扫描周期性变化，在经典三闭环控制下，雷达天线伺服控制精度在-900~1 600 urad之间周期性波动；基于扰动观测器的雷达天线伺服控制将扰动引入到输入端进行补偿，雷达天线伺服控制精度在-80~80 urad之间周期性波动。基于扰动观测器的雷达天线伺服控制精度明显优于经典闭环控制。当给定的扫描速度指令为30（°）/s时，经典三闭环控制扫描速度在15~45（°）/s之间变化；而基于扰动观测器的雷达天线伺服控制扫描速度在28~31.6（°）/s之间变化。表明基于扰动观测器的雷达天线伺服控制速度波动小，运行更平稳。

从图9~图10可以看出：当风速为20 m/s时，经典三闭环控制与基于扰动观测器的雷达天线伺服控制速度和位置精度的特性总体趋势与风速为10 m/s时的基本相同，只是量值增大。其中经典三闭环控制伺服精度在-1 100~1 850 urad之间周期性波动，扫描速度在13~47（°）/s之间变化；基于扰动观测器的雷达天线伺服控制精度在-92~100 urad之间周期性波动，扫描速度在27.6~32（°）/s之间变化。

在实际的使用环境下，基于扰动观测器的雷达天线伺服控制在不同的风速环境下速度的波动范围和位置精度与经典三闭环伺服控制相比均性能更优、环境适应性更强，可以使雷达系统在不同的实际应用环境中性能更优地进行稳定搜索、目标识别和跟踪定位，为态势感知和指挥决策提供判断依据。

5 结 论

（1）机载雷达天线结构尺寸大，伺服运动控制在实际典型应用场景下易受到空气阻力影响，本文建立了其伺服运动的动力学模型、伺服控制模型和扰动观测器模型，可用于扰动影响下的雷达天线伺服控制分析研究。

（2）对经典三闭环和基于扰动观测器雷达天线伺服控制进行了仿真和对比分析，仿真试验特性表明，机载雷达天线伺服控制扰动观测器控制性能更优。可为雷达天线伺服控制的应用提供参考，具有工程应用价值。