多物理效应的钙钛矿太阳能电池模型研究

张 骁,孙久勋,陈鹏斌,樊安琪

(电子科技大学 物理学院,四川 成都 611731)

太阳能电池是一种重要的可再生能源,进一步降低电池的成本并提高效率将使其应用更为广泛。近年来,有机-无机混合钙钛矿材料,例如CH3NH3PbX3,因其成本低廉、光的吸收系数高,有希望成为新一代低成本高效率太阳能电池的吸收材料[1-3]。

钙钛矿作为一种人工合成材料,在2009 年首次被尝试应用于光伏发电领域后,因性能优异、成本低廉、商业价值巨大,从此大放异彩。近年来,全球顶尖科研机构和大型跨国公司,如牛津大学、瑞士洛桑联邦理工学院、日本松下、夏普、东芝等都投入了大量人力物力,力争早日实现量产。

目前,已发表文献中关于钙钛矿太阳电池理论模型表述还不完善,或者只是从简单的能带模型出发来解释一些现象。因此很多理论科研工作者主要致力于两个大的方向对钙钛矿太阳能电池进行研究:内部参数和外部特性。内部参数包括载流子分布与传输、迁移率、电场分布等,外部特性包括伏安特性、光照影响、温度影响等。

然而,现有解释载流子运输的模型,许多都由于某些局限性而忽略了一些因素[4-5]。

例如式(1)是从Tress 等[6]、Sun 等[7]和Garcia-Belmonte[8]的研究中推导并用玻尔兹曼分布和高斯态密度修正得到的。

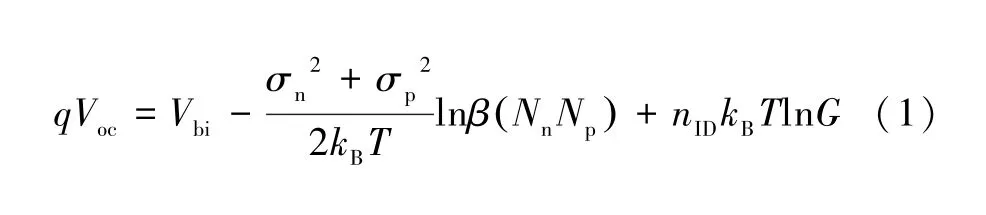
式中:Vbi是内建电压;σn(p)是电子(空穴)的态密度;kB是玻尔兹曼常数;T是温度;q是电子电荷;β是复合常数;Nn(p)是总的态密度;nID是理想因子;G是光生载流子的总数,与入射光功率(Pin)成正比。式(1)解释了Voc降低的原因(参考Garcia-Belmonte 和Bisquert 的研究[9])。

上述等式把载流子迁移率取成常数,载流子浓度用非简并玻尔兹曼统计研究,并且忽略了阳极和阴极势垒Wan、Wcat的影响。同时,大部分模型中的光生载流子并非一个关于坐标的函数而是取常值,也没有考虑到波长分布对入射光的影响。此外,至今为止大部分的理论工作都是数值模拟的。详细的数值模型提供了对电池基本性能瓶颈的深刻见解,但通常不适合快速表征、筛选和预测面板性能。

此前已有许多关于有机太阳能电池内部载流子输运原理的研究,特别是温度、复合、载流子生成、迁移率、约束条件等。钙钛矿太阳能电池的物理模型与有机太阳能电池有诸多相似之处,借鉴这些研究去创建一种更高效的钙钛矿太阳能电池模型值得尝试。由于内部参数很难直接测量得到,所以必须通过计算机模拟结合其对外部特性的影响来研究钙钛矿太阳电池的工作机理。

本文提出了一种考虑多种物理效应的钙钛矿太阳能电池的半解析模型,该模型使用费米-狄拉克分布研究载流子浓度,采用Pasveer 等[10]的迁移率模型μ(T,p,F),并建立了一个统一的电场强度函数;使用黑体辐射吸收公式代替太阳光谱进行计算,同时考虑了波长分布对入射光的影响,将光生载流子表示成关于坐标的函数。

该模型针对文献中报道的4 类钙钛矿太阳能电池进行了系统验证,实验数据与模型拟合较好;此外还找到了限制电池性能的可能原因。这对于准确和复杂的大规模网络仿真至关重要,更有助于提高钙钛矿太阳能电池性能的研究。

1 半解析模型

典型的钙钛矿太阳能电池由钙钛矿吸收层(300～500 nm)、空穴传输层(p 型)、电子传输层(n 型)和前后触点以各种结构排列。图1(a,b)中的传统结构分别以PEDOT ∶PSS 和PCBM 作为前空穴传输层和后电子传输层。然而,在倒置结构中,如图1(c,d)所示,TiO2是前电子传输层,而Spiro-OMeTAD 是后空穴传输层。此外,对于传统结构和倒置结构,都认为高效电池中的吸收层是本征的[11],见图1(a,c)。对于具有明显的p 型自掺杂的电池,工作模式会改变,效率会降低[12],见图1(b,d)。

因此,钙钛矿太阳能电池可分为(1 类)p-i-n[13]、(2 类)p-p-n[14]、(3 类)n-i-p[15]和(4 类)n-p-p[16]电池,相应的能带图如图1 所示[4]。

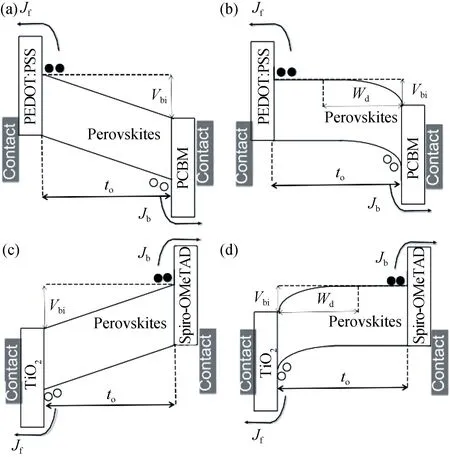
图1 传统结构(PE-DOT ∶PSS/Perovskite/PCBM)。(a) 1 类(p-i-n);(b) 2 类(p-p-n)和倒置结构(TiO2/Perovskite/Spiro-OMeTAD);(c) 3 类(n-i-p);(d) 4 类(n-p-p)钙钛矿太阳能电池的能带图[4]Fig.1 Energy diagram of perovskite solar cells in traditional structure(PE-DOT ∶PSS/Perovskite/PCBM).(a) Type-1 (p-i-n);(b) Type-2 (p-p-n) and titania-based inverted cells(TiO2/Perovskite/Spiro-OMeTAD);(c) Type-3 (n-i-p);(d) Type-4 (n-p-p)[4]

Xiong 等[17]于2019 年建立了一个有机太阳能电池的物理模型,在此模型基础上本文进行了改进并用于研究钙钛矿太阳能电池,最后对模型的合理性进行分析。此模型基于电流连续性方程(式(2))和修正后的漂移-扩散方程(式(10))。

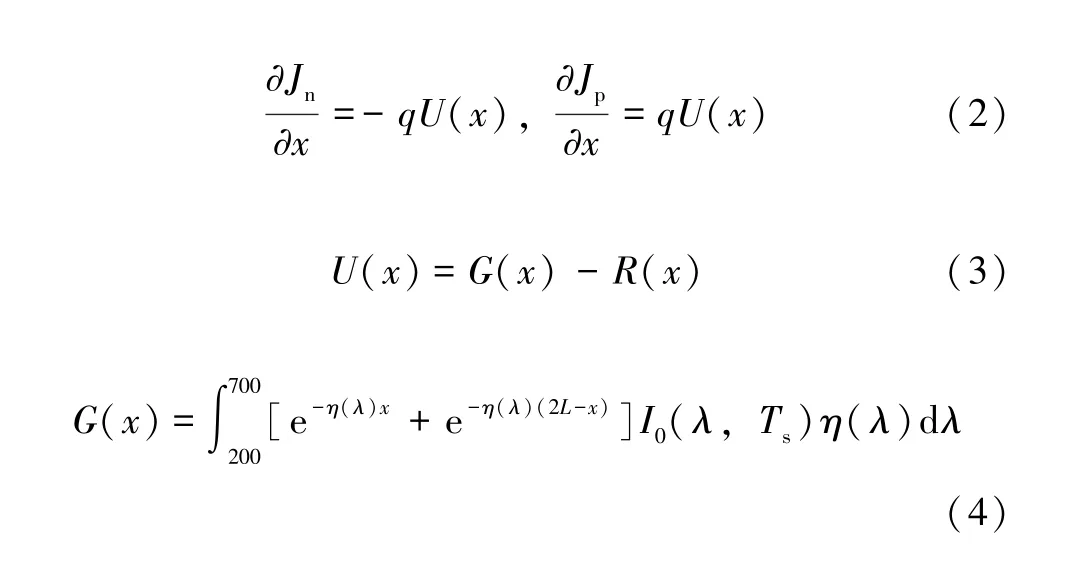
式中:Jn(p)是电子(空穴)的电流密度;U(x)是不同位置的净生成率;G(x)是光生载流子速率;R(x)是复合速率;η(λ)是与波长有关的吸收系数[18];I0(λ,Ts)是光源色温为Ts,波长为λ的入射光子通量,I0(λ,Ts)可以在使用一个修正因子kin的情况下通过普朗克黑体辐射公式模拟。

式中:υ是光的频率;v1,v2分别是波长为700 nm 和200 nm 光的频率;c是真空中的光速;h是普朗克常数;Pblk是黑体在温度Ts下的光功率。

在复合方程式(9)和漂移扩散方程式(11)中引入了平均浓度:

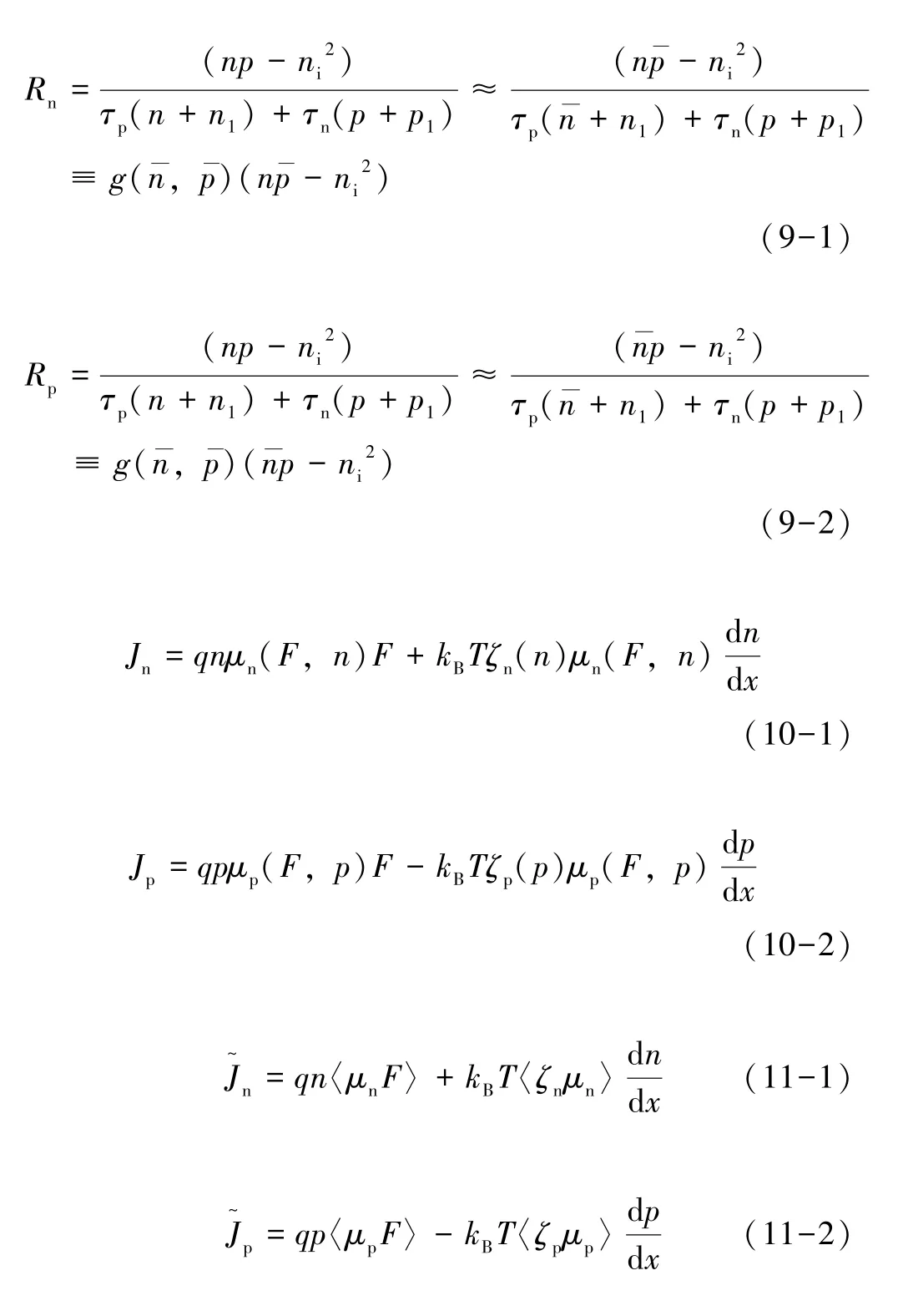
式中:n是电子浓度;p是空穴浓度;ni是本征载流子浓度;τn(p)是电子(空穴)的有效寿命,将其视为常数[19],并且它对Voc的影响特别小;n1和p1是非本征载流子浓度;是平均电子浓度;是平均空穴浓度;μn(p)是电子(空穴)迁移率。使用Pasveer 等的迁移率模型:

式中,μ(T,p) 是温度和载流子密度的函数。

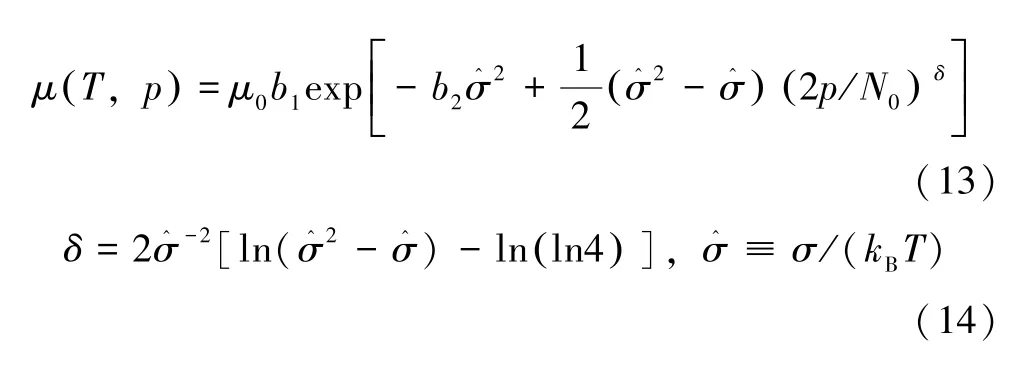
因为文献[20]指出Pasveer 等的式(13)中(pa3)不符合普遍化的标度性质,所以根据文献[20],把其中的(pa3)替换为(p/N0)。b1=1.8×10-9,b2=0.42。

f(T,F) 是温度和电场的函数:

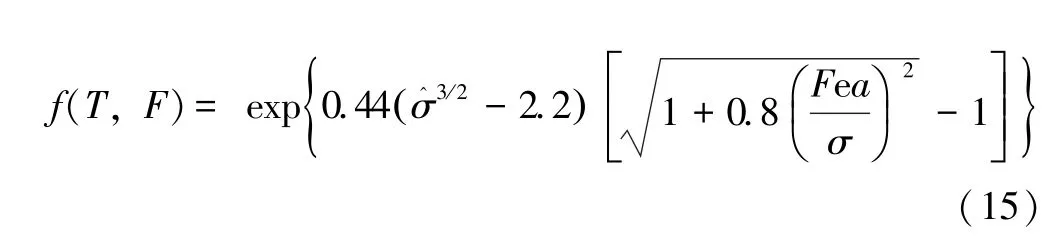
方程(11)中的平均量用下面的方程计算:

式中:a是晶格常数;ζn(p)是爱因斯坦系数,表征了简并度。可以通过费米-狄拉克分布得到初始载流子浓度和爱因斯坦系数。

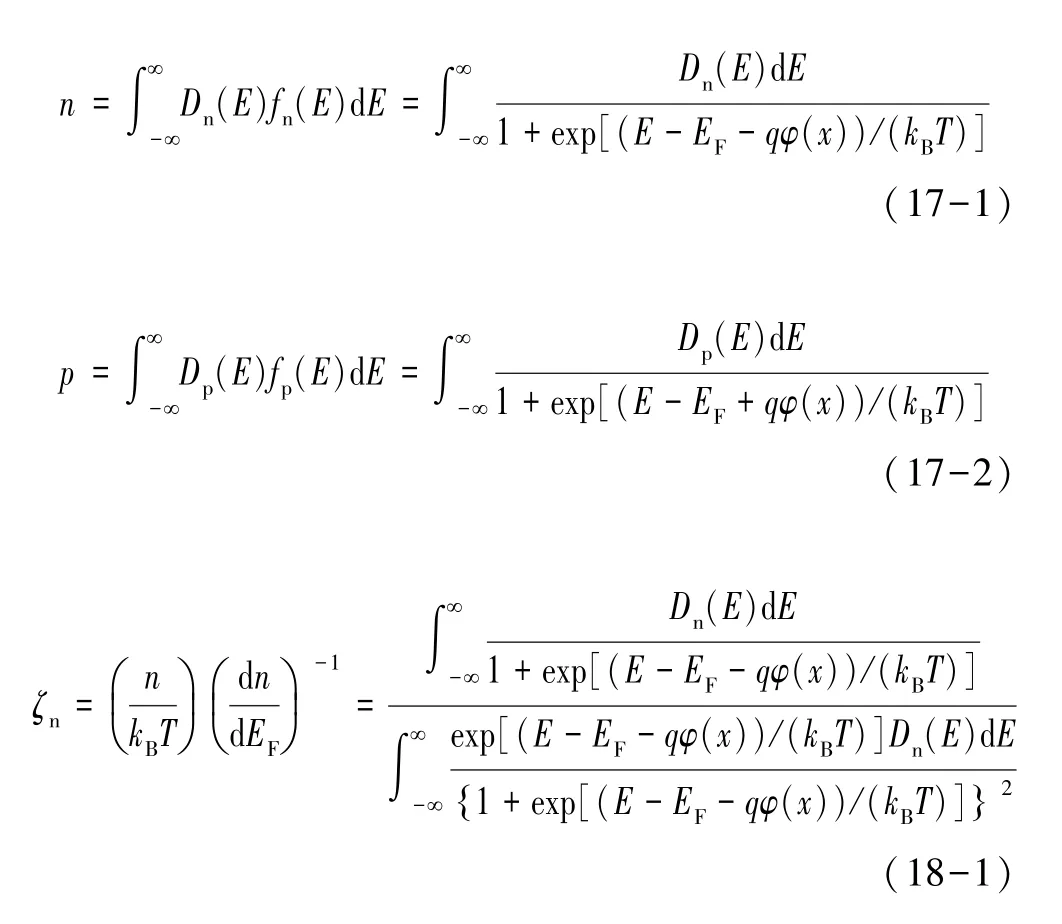
式中:φ(x) 是不同位置的电势;D(E)是态密度,为简单起见,在后面的计算中,把电子和空穴的态密度取相同的高斯态密度:

式中,σ是态密度宽度,代表了能量无序度。接下来,引入如下边界条件[5]:

式中:Eg是LUMO 和HOMO 间的禁带宽度;V是外加电压。

对于4 类不同的钙钛矿太阳能电池,提出如下的统一电场强度函数模型:

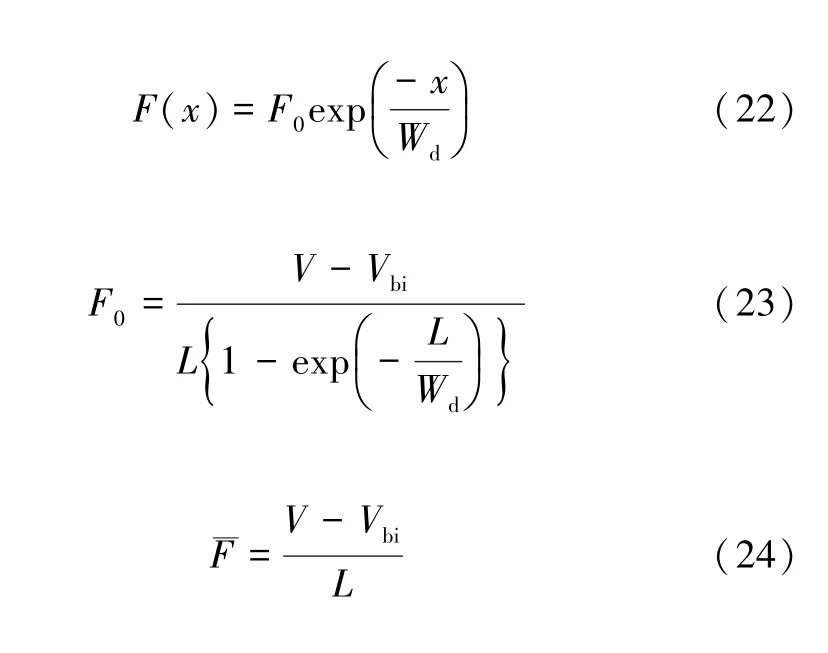
式中:L是本征层厚度;Wd是耗尽区宽度;是平均电场强度。对于1 类(n-i-p)和3 类(p-i-n)电池,其电场强度为常数,取Wd=∞。对于2 类(p-p-n)和4类(n-p-p)电池,Wd取值为小于L的常值。

联立式(2),(3),(9),(11),(22),(23),得到两个二阶微分方程:

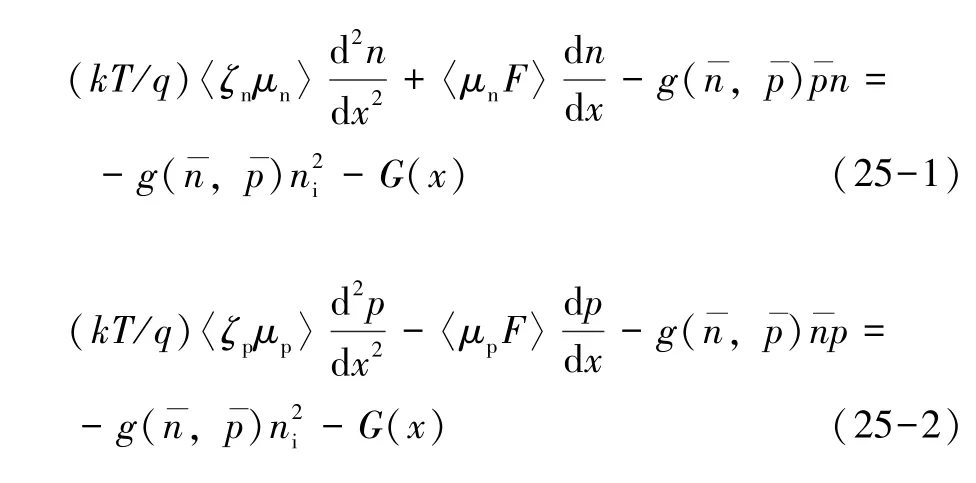
解这两个二阶微分方程,得到新的载流子浓度表达式:

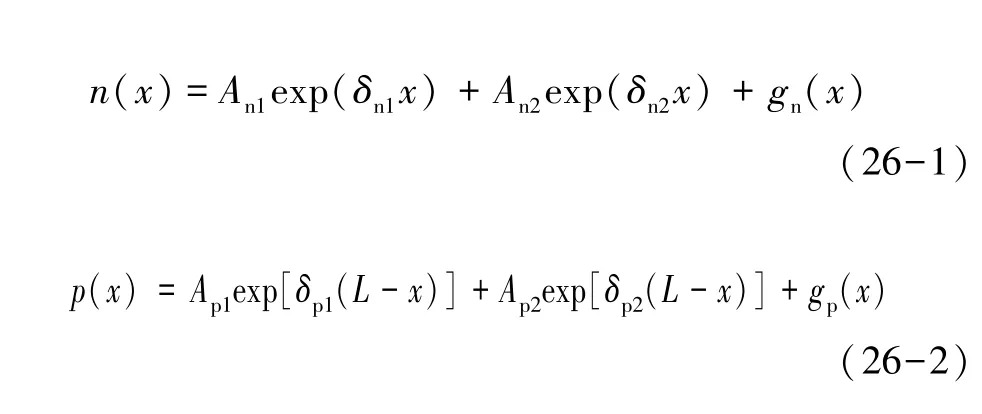
式中:An1,An2,Ap1,Ap2,δn1,δn2,δp1,δp2为中间变量;gn和gp是式(25)的特解,上述变量定义为:

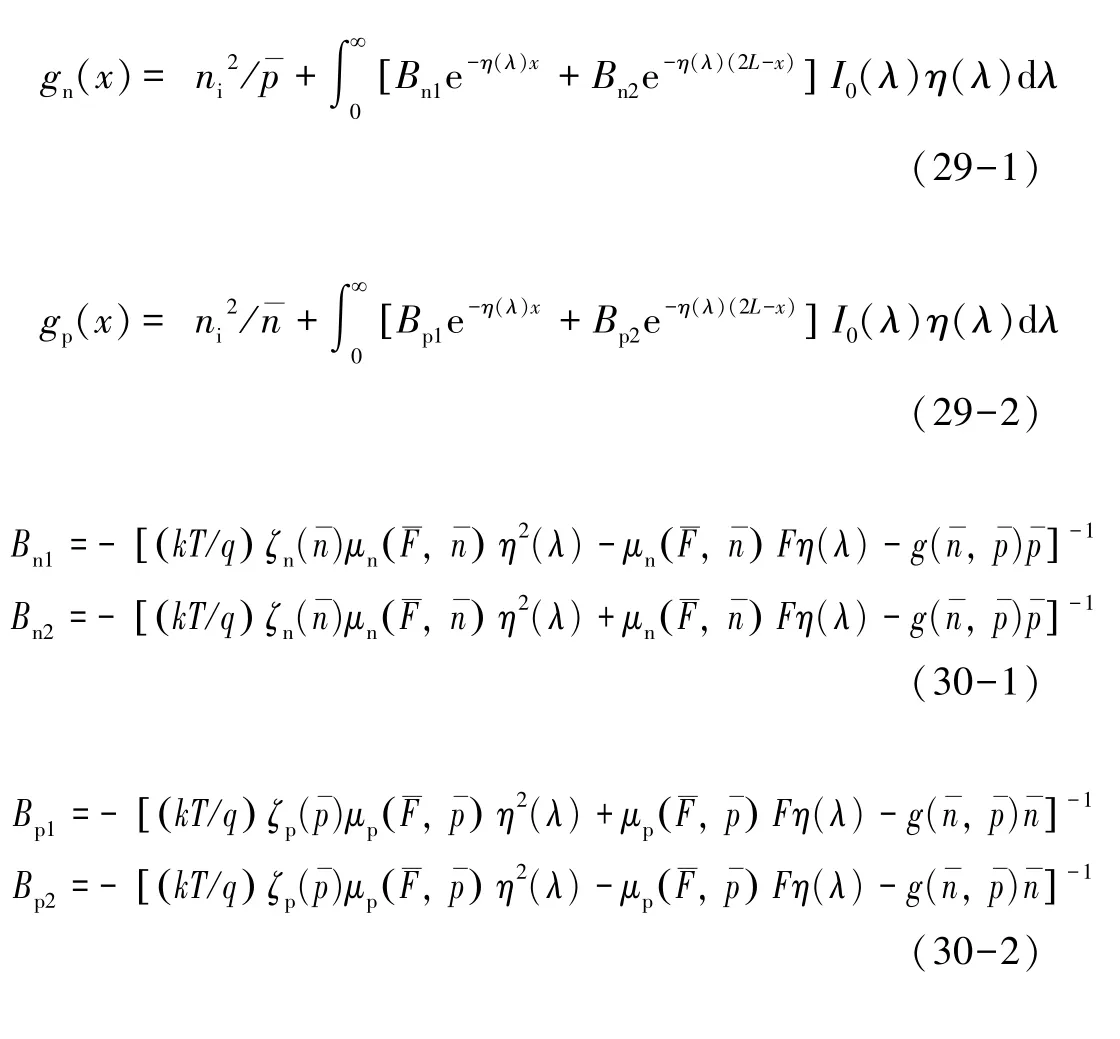
式中,n(0),n(L),p(0)和p(L)均是边界浓度,可通过式(17),(19),(20)得到。接下来,引入两个中间变量(式(31)),并依据式(17),(18),将他们转换成式(32)的形式,循环直至收敛。用最后的ζn(p)代表简并度,用最后的n和p来绘制J-V曲线。

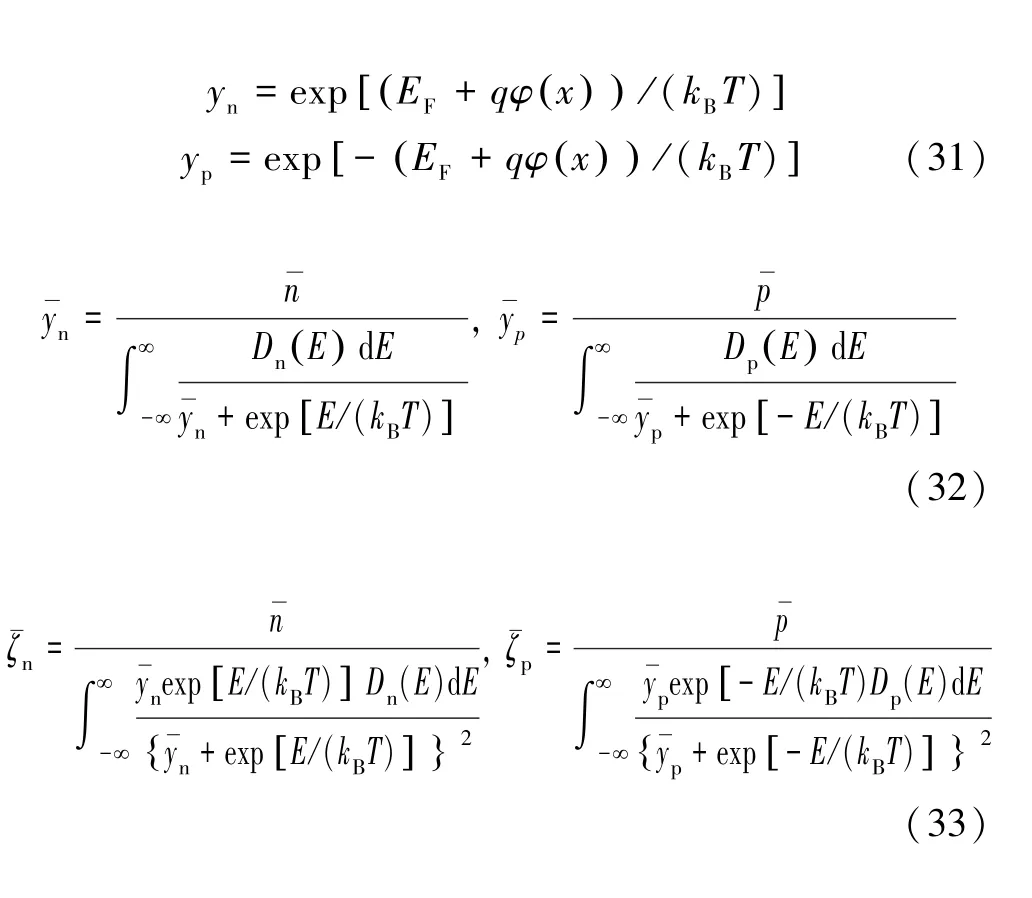
2 结果与讨论

为了验证模型的准确性,拟合了4 种不同类型的钙钛矿电池的光电流J-V曲线(图2～5)。样品#1 和#2是固溶处理的PCBM 基结构的电池[11](1 类和2 类),样品#3 和#4 分别是通过气相沉积和固溶处理制造的TiO2基倒置结构电池[21](3 类和4 类)。表1 汇总了这4 种样品的拟合参数取值。

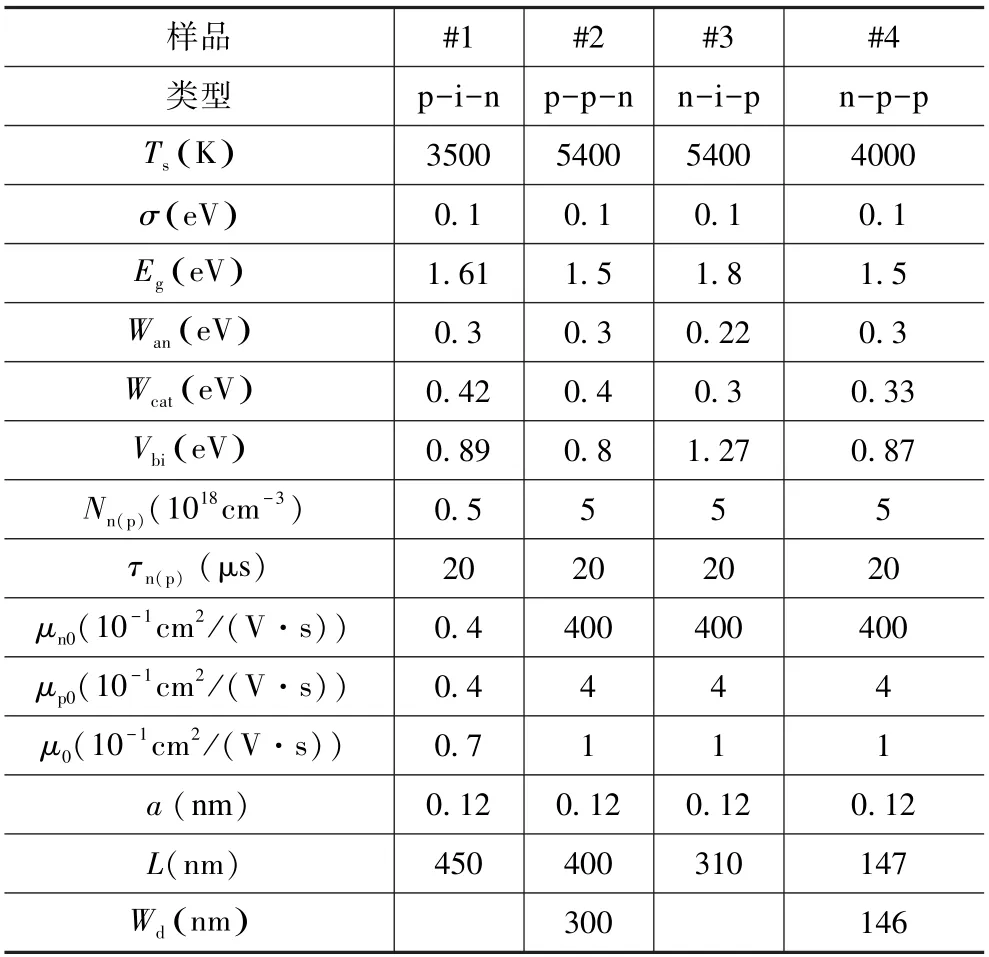
表1 4 种不同类型钙钛矿太阳能电池样品材料的参数取值Tab.1 Parameter of 4 different types of perovskite solar cell

在拟合数据之前,必须先知道太阳能电池的结构(例如是PEDOT ∶PSS/钙钛矿/ PCBM 结构还是TiO2/钙钛矿/ Spiro-OMeTAD 结构)以及吸收层是否为自掺杂的,以便将该电池与4 类钙钛矿电池相对应。

理想情况下,测量电池的电容-电压曲线可以得到掺杂的数据,但是从实验文献中得不到该信息。作为替代,发现低电压下的J-V曲线的斜率(dJ/dV)也可以区分自掺杂和本征电池。

具体来说,自掺杂器件的光电流在达到MPP(Maximum Power Point,最大功率点)之前大大降低(0～0.5 V),而本征器件的光电流在达到MPP 之前较为水平。通过上述方法便能为实验数据选择匹配的钙钛矿太阳能电池类型。

图2 和图3 的实验数据来自于Nie 等的研究,图4和图5 的实验数据来自于Liu 等的研究。综合图2～5可以发现4 种电池的实验数据与模型拟合都较好。

图2 样品#1(1 类(p-i-n))的实验数据和J-V 特性曲线Fig.2 Sample #1's (Type-1(p-i-n)) experiment data and J-V characteristic

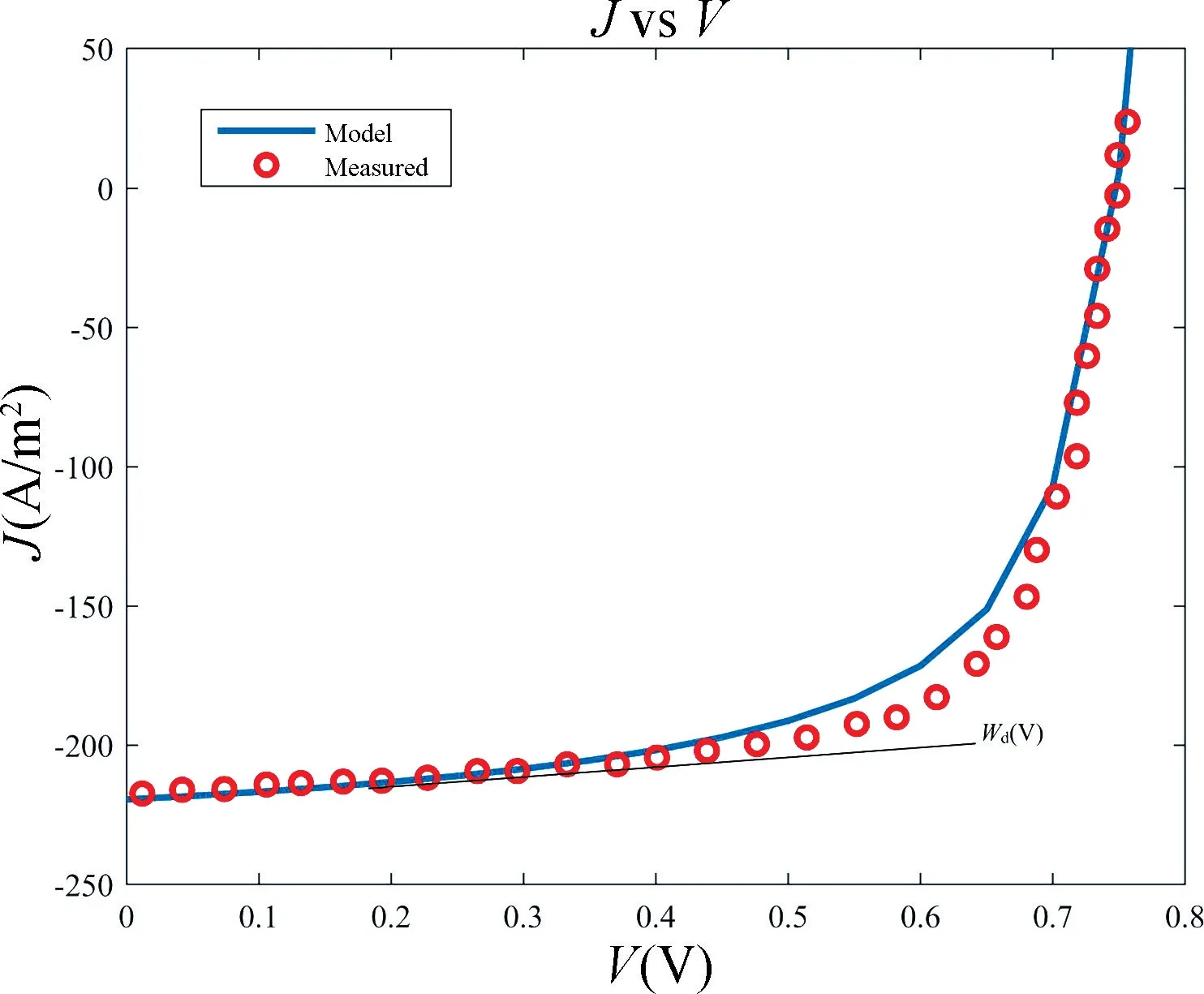
图3 样品#2(2 类(p-p-n))的实验数据和J-V 特性曲线Fig.3 Sample #2's (Type-2(p-p-n)) experiment data and J-V characteristic

图4 样品#3(3 类(n-i-p))的实验数据和J-V 特性曲线Fig.4 Sample #3's (Type-3(n-i-p)) experiment data and J-V characteristic

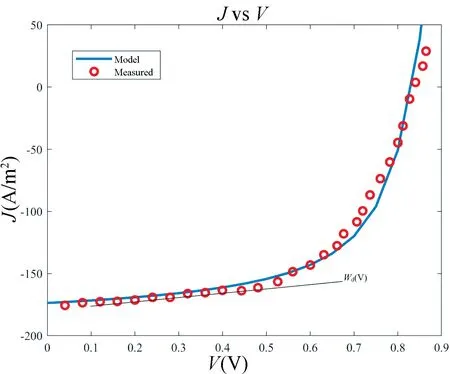
图5 样品#4(4 类(n-p-p))的实验数据和J-V 特性曲线Fig.5 Sample#4's (Type-4(n-p-p)) experiment data and J-V characteristic

图3 和图5 表明,自掺杂器件的光电流J-V曲线在达到最大功率点之前有一个急剧下降(0～0.5 V)。事实上,该特征可能与在电池制造期间引入的缺陷或杂质引起的自掺杂效应相关。本研究的模型将这种2型和4 型电池光电流的线性下降解释为p-n 结耗尽区Wd(V)(或者说空间电荷区)的电压下降。如果没有基于物理的模型,这一特性很容易被误认为是寄生电阻。

与具有相同结构的本征电池相比,自掺杂器件还具有较低的Vbi,从而导致较低的Voc(参见表1 和表2)。因此,限制样品#2 和#4 性能的主要因素是由于自掺杂效应导致的电荷收集效率的降低。

表2 4 种钙钛矿太阳能电池的性能参数Tab.2 Performance parameters of 4 types of perovskite solar cells

在研究本征器件#1 和#3 时,注意到#1 具有最高的填充因子(FF),但是其Voc比#3 小0.22 V(见表2)。Voc的降低可以用较低的Vbi来解释,这是由具有传统结构的钙钛矿电池传输层中的能带失配和较低的掺杂浓度共同导致的,上述因素是#1 的主要性能限制。另一方面,#3 的FF 较低,这是由于两个接触面的复合速率较高,表明无法充分阻止电荷流失。

即使#1 和#3 具有相近的能量转化效率,本文模型也证明了其基本性能限制的因素是不同的。

3 结论

本研究建立了一个半解析模型来描述4 种不同类型[p-i-n/p-p-n 和n-i-p/n-p-p] 的钙钛矿太阳能电池的光电流的伏安特性。该模型使用费米-狄拉克分布研究载流子浓度,采用Pasveer 等的迁移率模型μ(T,p,F),并建立了一个统一的电场强度函数F(x);使用黑体辐射吸收公式代替太阳光谱进行计算,同时考虑了波长分布对入射光的影响,将光生载流子表示成关于坐标的函数。

低电压下的J-V曲线的斜率(dJ/dV)也可以区分自掺杂和本征电池。自掺杂器件的光电流在达到,最大功率点之前大大降低(0～0.5 V),而本征器件的光电流在达到最大功率点之前较为水平。通过上述方法便能为实验数据选择匹配的钙钛矿太阳能电池类型。该模型针对文献中报道的4 类钙钛矿太阳能电池进行了系统验证,实验数据与模型拟合较好,证明了该模型的准确性。

此外,该模型找到了限制4 类钙钛矿太阳能电池基本性能的不同因素。限制样品#2 和#4 性能的主要因素是由于自掺杂效应导致的电荷收集效率的降低。具有传统结构的钙钛矿电池传输层中的能带失配和较低的掺杂浓度是样品#1 的主要性能限制。两个接触面的复合速率较高,表明无法充分阻止电荷流失是样品#3的主要性能限制。

通过该模型的验证,结合其他测量技术,为表征、优化和筛选钙钛矿太阳能电池提供了一种简单且互补的方法。