协作式巡航控制下混合车队队列稳定性

李淑庆，李啟丰，王昊，秦严严

(1.重庆交通大学，交通运输学院，重庆400074；2.昆明市规划设计研究院，昆明650041；3.东南大学，交通学院，南京210096)

0 引言

针对协作式巡航控制(Cooperative Adaptive Cruise Control，CACC)交通流稳定性的研究，国外研究开展较早，研究成果大致可以分为3 类。第1类研究以交通流仿真为技术手段，分析某种情形下CACC 的混入是否可有效提升传统车流的不稳定性[1]；随后，Talebpour等[2]应用李雅普诺夫理论对混入不同比例CACC 车辆的混合交通流稳定性进行理论分析，该研究成果已成为目前主流研究方法；第3类研究主要以控制论为方法论，对由CACC车辆和人工驾驶车辆构成的混合车队队列稳定性进行分析与计算，以此进行CACC跟驰控制的相关参数设计与策略优化[3]。

国内学者王昊等[4]从理论层面分析了当自适应巡航控制(Adaptive Cruise Control,ACC)车辆不稳定时，CACC车辆应如何提升混合交通流稳定性的问题，研究结果可为CACC控制器的顶层设计提供参考。华雪东等[5]从提高交通流稳定性层面，对CACC控制系统进行了改进设计，并通过数值仿真实验论证了设计方法有利于提升混合交通流稳定性。秦严严等[6]从CACC 混合交通流稳定性的角度，理论计算了CACC车头时距与稳定性的解析关系，提出了一种随CACC比例而动态变化的CACC车头时距设计策略。

由此可见，现有研究成果集中在：CACC 比例对混合交通流稳定性的影响，且已得到CACC比例增加有利于提升混合交通流稳定性的结论；以混合车队稳定性为优化目标的CACC 跟驰参数控制策略，并在CACC车头时距以及反馈增益等方面形成较成熟的结论。但是，鲜有研究成果探讨连续多辆人工驾驶车辆的上游需要跟随至少几辆CACC 车辆的问题，而该问题的探讨能够为大规模CACC实地测试的实施提供前瞻性评估分析。鉴于此，本文对此开展研究，旨在为未来大规模混合车队实地测试的实施提供理论依据。

1 问题描述与建模

1.1 CACC混合车队

在由CACC 车辆和人工驾驶车辆构成的随机混合车流中，可抽象出如图1所示的混合车队。在图1 中，混合车队的前面有n辆人工驾驶车辆，随后为m辆的CACC/ACC 车辆，且在m辆CACC/ACC车辆中，鉴于人工驾驶车辆无车车通讯功能，紧跟其后的为ACC 车辆，ACC 车辆依托车载检测设备实现自主式自动驾驶，随后的m-1 辆为CACC 车辆，可与前车进行车车通讯，实现网联式自动驾驶。因此，混合车队中m和n的取值可体现CACC混合车队的规模。

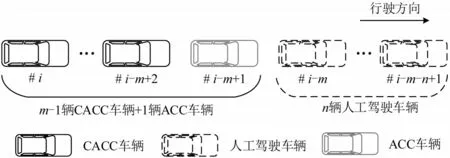
图1 CACC混合车队Fig.1 Platoon mixed with CACC vehicles

1.2 车辆跟驰模型

针对人工驾驶车辆而言，学者们研究了诸多跟驰模型，模型之间各有优劣，本文选择应用较广的优化速度模型(Optimal Velocity Model,OVM)作为人工驾驶车辆跟驰模型[7]，模型公式为

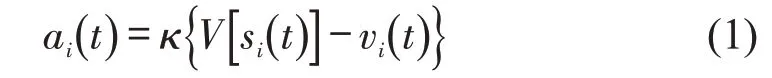
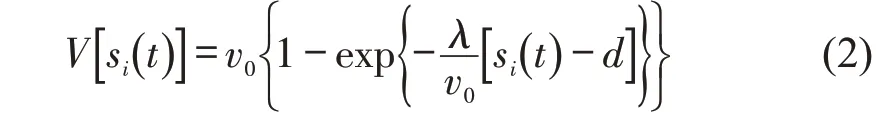
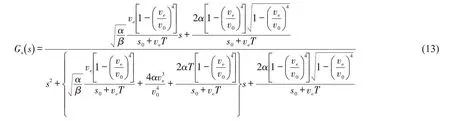
式中：v0为自由流速度；λ为敏感系数；d为安全间距。通过实测数据标定的模型参数值分别为[7]：v0=33.3 m·s-1，κ=0.70 s-1，λ=0.99 s-1，d=1.62 m。

针对CACC 车辆而言，根据文献[8]的研究成果，选择CACC车辆跟驰模型为

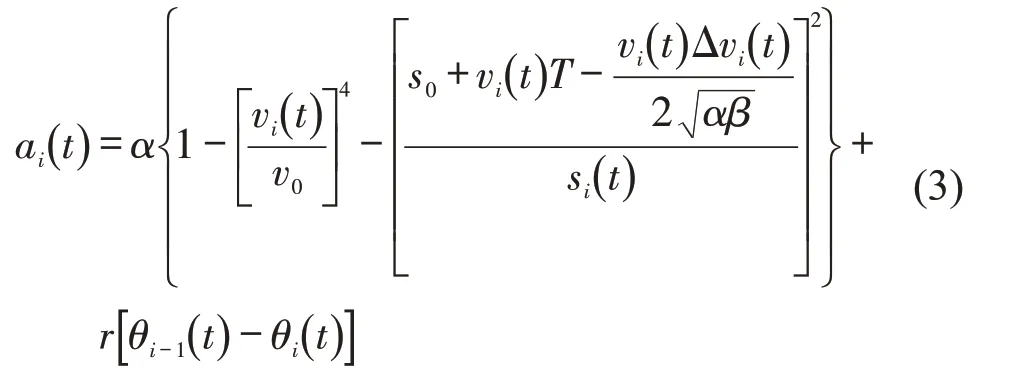
式中：α为最大加速度；β为舒适减速度；s0为最小间距；T为安全车头时距；为为车辆i与前车i-1 在时间t时的速度差；r为敏感系数；、分别为CACC车辆i、i-1 在时间t时的电子节气门角度。

式(3)中CACC 车辆跟驰模型考虑了前后相邻车辆的自动控制系统中的电子节气门角度，根据文献[8-10]，电子节气门角度控制可与CACC 车辆的运行速度及加速度建立数学模型为

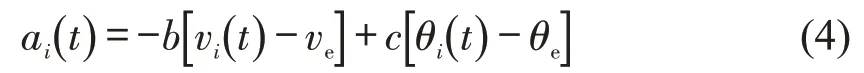
式中：b与c为系数；ve为平衡态速度；θe为CACC车辆保持平衡态速度时的电子节气门角度。参数取值为[8-10]：r=0.5，b=0.8，c=0.27。

针对ACC车辆而言，在无前车通讯的条件下，式(3)中的CACC车辆跟驰模型退化为ACC车辆跟驰模型，模型结构为

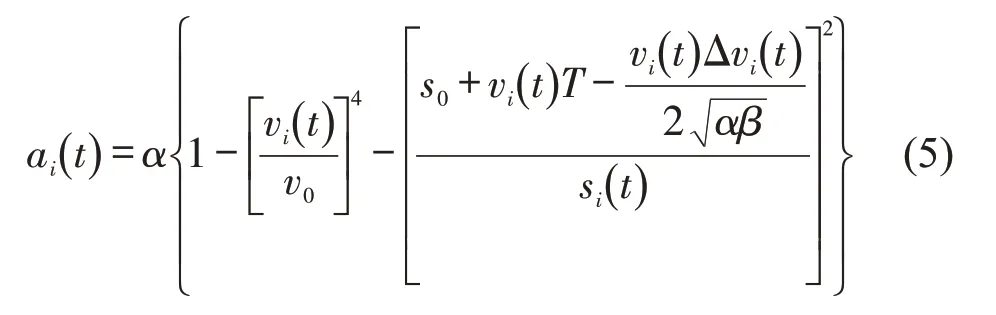
根据文献[2]，模型参数取值为：v0=33.3 m·s-1，α=4.0 m·s-2，s0=2 m，T=2.0 s，β=2.0 m·s-2。

2 队列稳定性分析

理论推导混合车队的队列稳定性判别条件，并针对m和n取不同值时的混合车队情形，计算出对应的稳定性分析结果。

2.1 理论推导

针对人工驾驶车辆而言，采用泰勒公式对式(1)在平衡态展开，得到

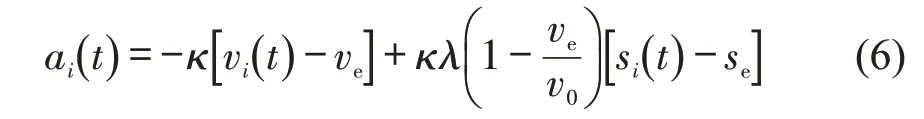
式中：se为平衡态车间距。

定义车流扰动为

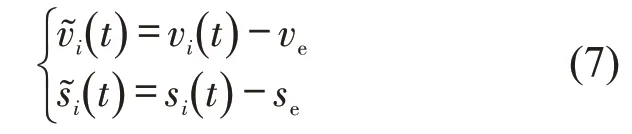
将式(7)带入式(6)计算得到

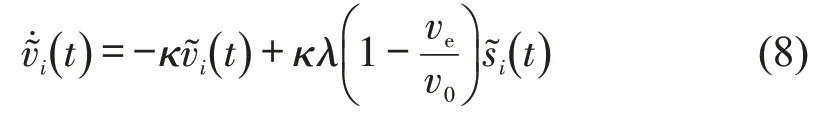
将式(8)进行拉普拉斯变换，计算得到人工驾驶车辆应对扰动时的传递函数为

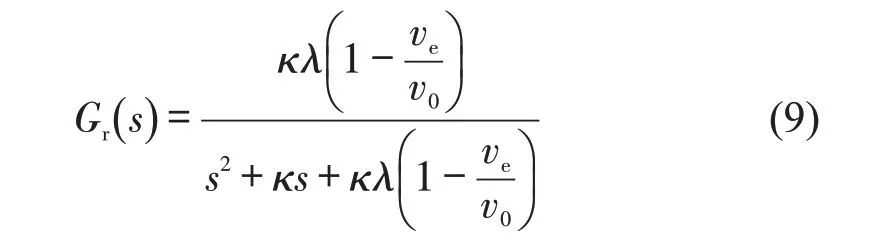
式中：s为拉普拉斯算子。

令s=jw，将由拉普拉斯域转变至频率域，即

式中：w为角频率。

同理，针对CACC 车辆而言，将其模型公式在平衡态进行泰勒展开，并将式(7)中定义的扰动带入，最终计算得到

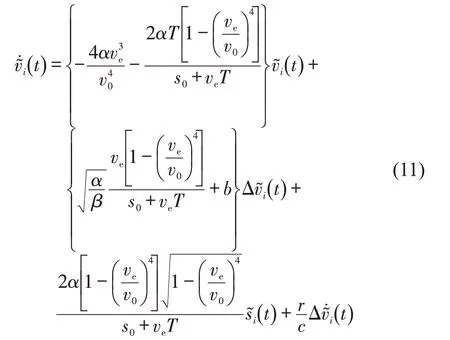
将式(11)进行拉普拉斯变换，计算CACC 车辆对应的传递函数为

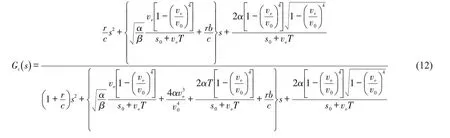
基于CACC 车辆与ACC 车辆的跟驰模型结构，当r=0 时，可通过式(12)获取ACC 车辆对应的传递函数为

令s=jw，可分别将与由拉普拉斯域转变为频率域，即

根据图1所示的CACC 混合车队，将车队头车的行驶状态作为扰动输入，考察尾车CACC车辆对扰动的抑制能力，计算混合车队的队列稳定性判别条件为

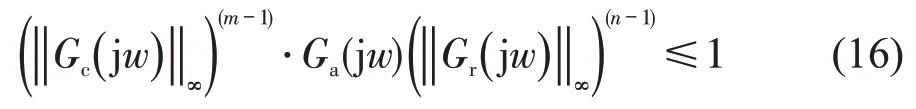
2.2 结果分析

应用2.1 节推导得到的稳定性判别准则，计算不同m和n取值情形下混合车队的队列稳定性结果，如图2所示。在图2中，计算了m取不同值时，混合车队关于车流速度与混合车队中人工驾驶车辆数n的稳定域情况，其中，白色区域表示不稳定区域，黑色区域表示稳定区域，由此可以看出，随着m的增加，混合车队的稳定域在全速度范围内呈现出增加的趋势。具体而言，以m=4 的情形为例进行说明，即混合车队中存在1 辆ACC 车辆和3 辆CACC 尾车，此时混合车队稳定性计算结果如图2(d)所示，可以看出，对于任意的车流速度而言，若要使得混合车队在全速度范围内均能够保持稳定状态，则混合车队中连续人工驾驶车辆数n不能超过5辆。

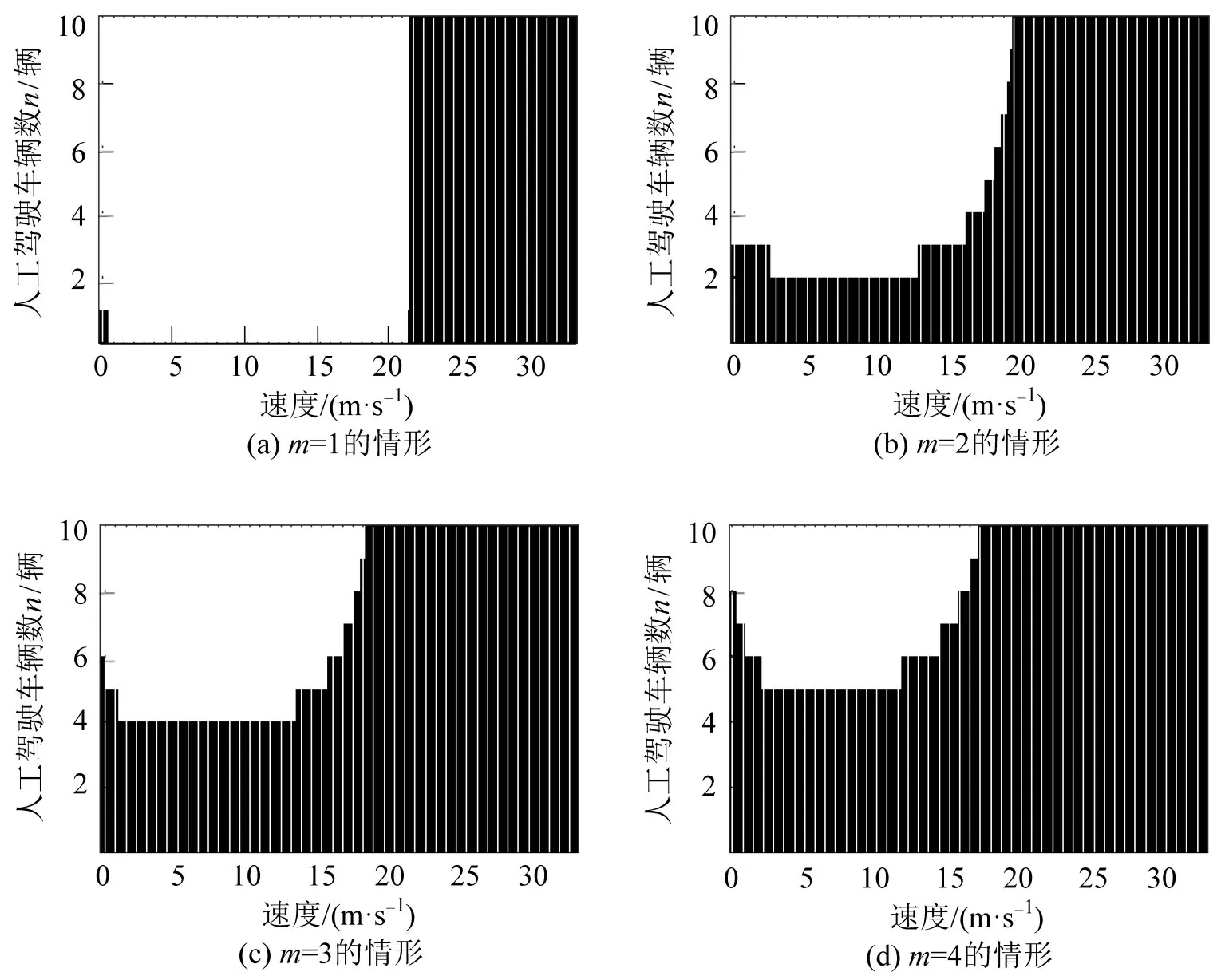
图2 混合车队队列稳定性结果Fig.2 Results of string stability of mixed platoon

以混合车队在全速度范围内均稳定为条件，计算m取不同值时，n能够达到的最大值情况，以此分析在全速度范围内稳定的混合车队中，CACC车辆应当占有的比例，计算结果如表1所示。表1中，当m=1，即车队中仅有1 辆ACC 车辆，且无CACC车辆，使得混合车队中亦无人工驾驶车辆，此时不构成混合车队，故该特殊情况不予考虑。m取值从2增至10的过程中，若要混合车队在全速度范围内稳定，则n可取的最大值依次为2、4、5、6、7、8、9、11 与12，即在混合车队中，要求CACC 比例应当不低于25.00%～41.17%。

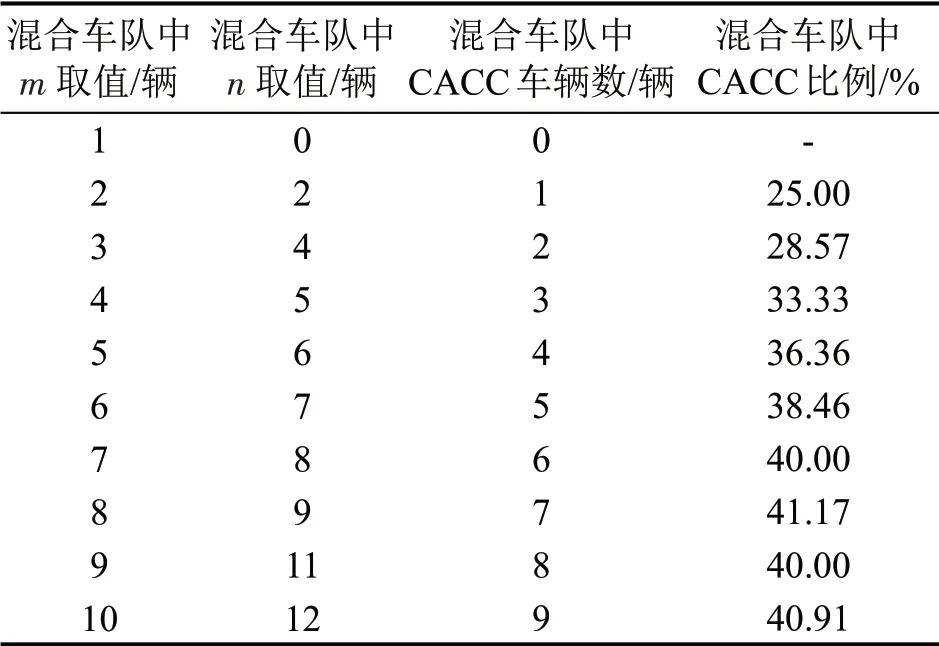
表1 混合车队全速度范围稳定时m 与n 的比例关系Table 1 Propotional relationship of m and n when mixed platoon is stable for all speeds

2.3 通用性证明

对于人工驾驶车辆及CACC车辆而言，现有跟驰模型并不局限于本文1.2 节所用模型，为了论证2.1 节理论推导的通用性与普适性，需验证上述理论推导过程同样适用于其他类型跟驰模型。

纵观现有人工驾驶车辆跟驰模型，无论跟驰模型结构如何，均可用一般性函数式表达，即

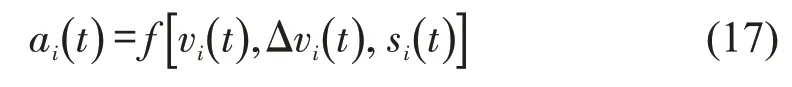
式中：f为人工驾驶车辆跟驰模型的函数式。

同理，参照现有相关研究成果[8-10]，将CACC 跟驰模型表达为通用性模型结构，即

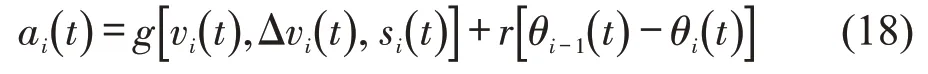
式中：g为CACC车辆跟驰模型的函数式。

当不存在V2V 通讯环境时，式(18)中r=0，则CACC 车辆通用性模型结构退化为ACC 车辆的通用性跟驰模型结构，即

针对人工驾驶车辆通用性跟驰模型结构而言，对式(17)进行泰勒公式展开，得到

式中：fv、fΔv和fs分别为人工驾驶车辆通用性跟驰模型函数式f在平衡态对速度、速度差和车间距的偏微分，计算公式为

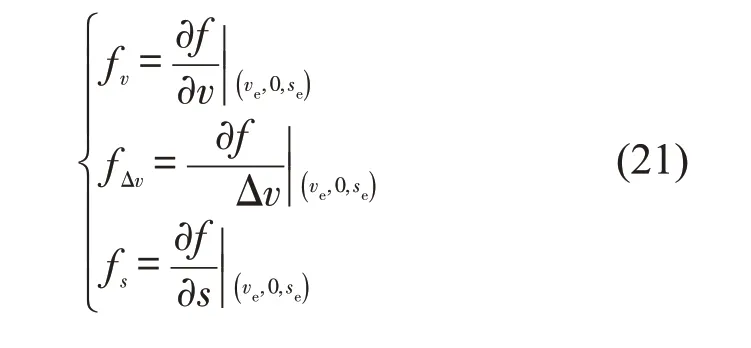
将式(7)中定义的交通流扰动代入式(20)中，计算得到

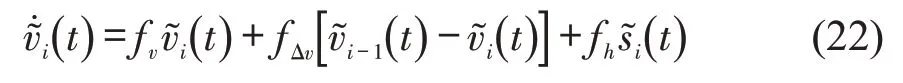
应用控制理论对式(22)两边进行拉普拉斯变换，计算关于人工驾驶车辆通用性跟驰模型函数式的传递函数为

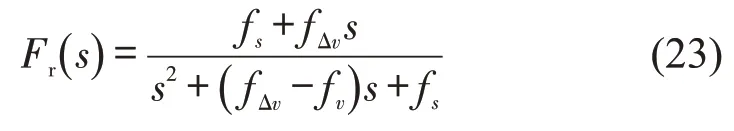
同理，对于CACC 车辆的通用性跟驰模型而言，对式(18)进行泰勒公式展开，并将式(7)中定义的交通流扰动代入，计算得到

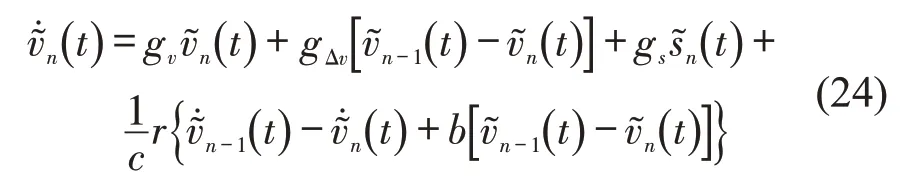
式中：gv、gΔv和gs分别为CACC 模型函数式g在平衡态对速度、速度差和车间距的偏微分，即

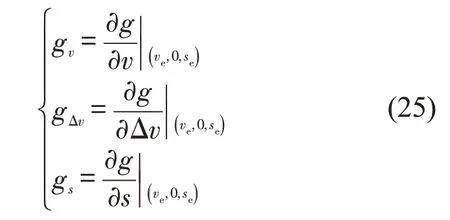
针对式(24)，进行拉普拉斯变换，计算关于CACC 车辆通用性跟驰模型函数式的传递函数为

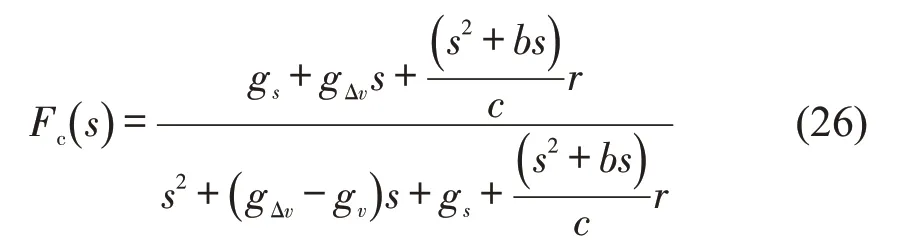
式(26)中，当r=0 时，退化为ACC车辆通用性跟驰模型的函数式的传递函数，即

令s=jw，将传递函数和由拉普拉斯域转变至频率域，分别得到

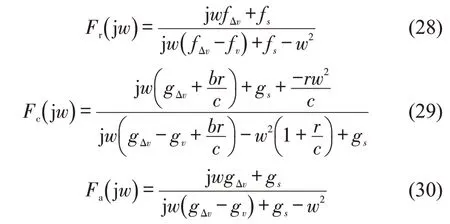
根据1.1 节定义的CACC 混合车队，得到混合车队队列稳定时应满足的判别准则为

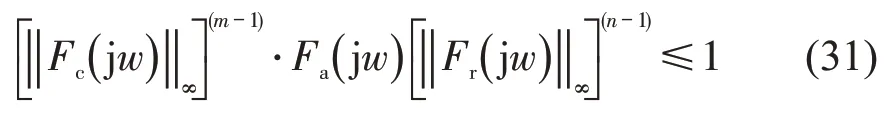
通过以上推导，即可得到通用性的混合车队队列稳定性判别准则。可以发现，当按照1.2 节选择的跟驰模型时，人工驾驶车辆和CACC车辆通用性跟驰模型函数式的偏微分项分别为

综上所述，本文针对混合车队队列稳定性判别准则的推导不受人工驾驶车辆以及CACC 车辆跟驰模型选取的限制，具备通用性和普适性。此外，本文选用的人工驾驶车辆跟驰模型得到实测数据的标定和验证[7]，而目前用于CACC 跟驰模型标定的实测数据尚难以获取，国际上普遍采用已有研究成果中公认的模型作为CACC 车辆跟驰模型。当使用不同的CACC跟驰模型时，鉴于CACC同质车流稳定性优于人工驾驶车流稳定性，本文上述理论计算结果的定性化结论不受影响。而定量化的结果会随着CACC跟驰模型的不同而发生改变，其原因在于，每种定量化结果本质上揭示了各CACC模型所描述的CACC跟驰控制策略的稳定性特征，因此，本文上述理论推导可在CACC大规模实车测试前，为相关CACC跟驰控制策略进行前瞻性评估。

3 数值仿真

以上述混合车队的队列稳定性为仿真对象，设计数值仿真实验，在给定平衡态速度下，仿真分析混合车队在m和n固定取值时的稳定性，以验证理论分析结果。

仿真实验中，混合车队按照图1 进行设定，在仿真初始时刻，混合车队以平衡态速度15 m·s-1行驶，假设车队前方有一虚拟扰动车，该扰动车初始时刻也以15 m·s-1的平衡态速度行驶，此时整个混合车队处于平衡态。在某一时刻，扰动车以1 m·s-2的恒定减速度减速至13 m·s-1，并以13 m·s-1的速度行驶至仿真结束，在这一过程中，混合车队头车(即人工驾驶车辆)将会受到扰动的影响，从而将该扰动传递至车队上游各车辆。因此，在仿真实验中，考察混合车队尾车(即CACC车辆)对头车(即人工驾驶车辆)的抑制效果，若尾车CACC 能够有效抑制头车在扰动下的速度波动，则从数值仿真的角度看，混合车队处于稳定状态；否则，不稳定。数值仿真实验在Matlab 软件中进行，仿真步长设置为0.1 s，仿真结果如图3所示。

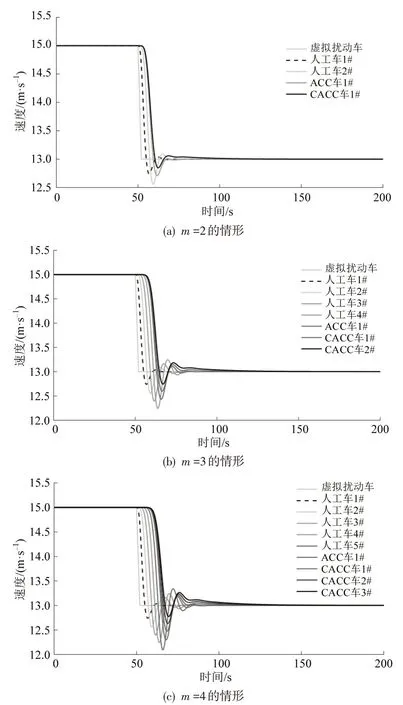
图3 混合车队稳定性数值仿真结果Fig.3 Stability results of numerical simulations of mixed platoon

由图3可以看出，人工驾驶车辆会将扰动逐步放大，当扰动传递至CACC 车辆时，CACC 车辆可有效逐步抑制扰动的放大，促进混合车队的稳定性。为了定量化分析尾车CACC 对头车人工驾驶车辆的扰动抑制作用，以速度的最大波动幅度为考察对象，计算图3 中3 种情形下的速度最大波动幅度，速度最大波动幅度定义为车辆速度与平衡态速度13 m·s-1之间的最大差值，计算结果如表2 所示。由表2 可知，3 种情形下车队尾车的速度最大波动幅度均小于车队头车的速度波动最大幅度，表明车队处于稳定状态，与理论分析结果一致。

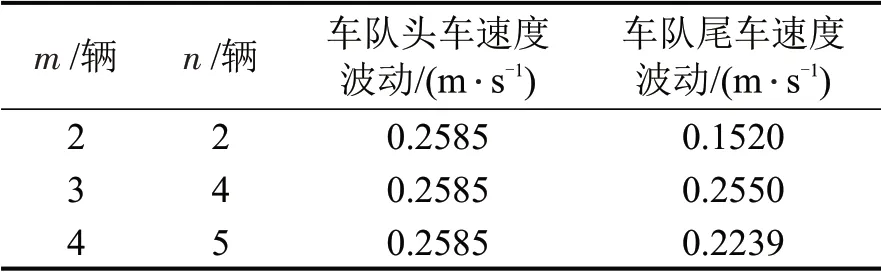
表2 速度最大波动幅度对比Table 2 Comparison of maximum fluctuation amplitude of speeds

4 结论

(1)基于人工驾驶车辆和CACC 车辆跟驰模型，理论推导混合车队队列稳定性判别准则，并论证了稳定性判别准则的理论推导具备通用性和普适性特点，能够适用于不同跟驰模型的选择。

(2)基于所推导的混合车队队列稳定性判别准则，混合车队队列稳定性由混合车队中CACC车辆数量、人工驾驶车辆数量以及车流速度共同决定，CACC车辆有利于提升混合车队稳定性，可有效抑制人工驾驶车辆的不稳定性。从定性化角度看，以混合车队在全速度范围内稳定为目标，随着混合车队中CACC车辆数量的增加，混合车队中可允许的人工驾驶车辆数量的上限值亦随之增加。从定量化角度看，若要满足混合车队全速度范围内稳定的要求，混合车队中CACC 车辆比例至少应达到25.00%～41.17%。

(3)若未来基于新的CACC控制策略而提出新的CACC跟驰模型，则本文所得定量化结论将发生变化，但是，鉴于CACC 车流稳定性优于人工驾驶车流稳定性的特点，本文所得定性化结论不受影响。同时，届时仍可依据本文所推导的通用性混合车队稳定性准则，评估相关CACC跟驰策略在混合车队稳定性方面的性能，为CACC大规模实地测试的实施提供科学依据。