基于螺旋理论的可变刚度机械臂关节研究

陈龙凯，张帆，蒋家鹏，于潇潇，吴凯宇

（1.201620 上海市 上海工程技术大学 机械与汽车工程学院；2.201620 上海市 上海工程技术大学 机器人智能控制实验室）

0 引言

手术机器人在手术过程中，末端手术器械要进入病人体内，所以，要防止手术器械对病人身体进行额外的破坏[1]，希望手术器械在到达指定位姿后，前端的机械臂关节能够进行有效的锁紧，以保证末端手术器械的稳定。因此，对机械臂关节进行研究很有意义。

目前，手术机器人关节常用的锁紧方式有液压锁紧、偏心锁紧和电磁锁紧。北航机器人研究所在对手术机器人的研究中采用了3 种锁紧机构：一种是电磁离合器锁紧机构。通过离合器的开合实现关节的松弛与锁紧[2-4]，但是由于电磁离合器的体积大，不适于手术机器人机械臂上使用；另一种则是弹簧锁紧机构。这种装置利用弹簧拉紧外圈，通过外圈与摩擦片抱死的方式实现锁紧，但弹簧长久使用，摩擦力不能保证恒定；第3 种通过液压锁紧装置来实现关节的锁紧。液压装置一般用于机床、大型起重设备，而且对于手术环境不能够保证。针对上述问题，本文提出了一种可实现锁紧的机械臂关节，通过ADAMS仿真验证和3D 打印件进行分析验证，最终确定该关节的可行性。

1 关节机构描述

1.1 设计原则

机构约束螺旋系。关节具有一个转动自由度，通过机构的运动螺旋系，求解反螺旋得到关节机构的约束螺旋系为5 系。

（2）分支约束螺旋系。由机构的约束螺旋系可计算分支的约束螺旋系，机构的约束螺旋系由2 条并行支链提供，机构约束力为各支链的末端约束力的并集。右侧支链具有5 个约束力，左侧分支的约束力不能超出该范围[5]。

1.2 关节构型介绍

所提出的关节模型如图1 所示，由上平台、下平台和2 条分支链所组成。其中，左侧支链由依次连接的6 个转动副和连接各转动副之间的连杆组成，两端的连杆与上下平台固连；右侧支链由一个转动副和连杆组成。两端的连杆同样与上下平台固连，其中，左右两侧支链均有一个主动运动副，其余均为被动副。

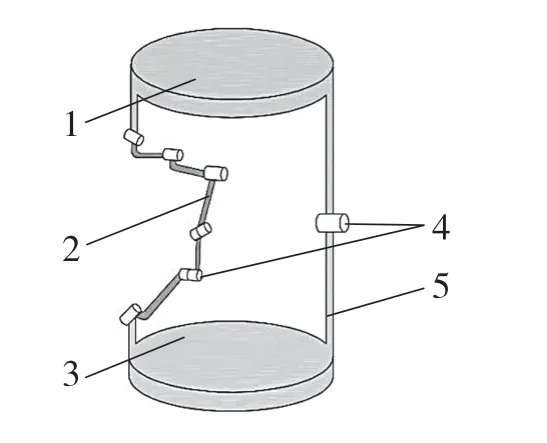
图1 关节三维模型Fig.1 Three-dimensional model of joints

1.3 锁紧条件

具体实现方式如图2 所示。首先假设Ri表示第i 个转动副，在初始位姿时，R1，R3，R6三个转动副的轴线空间汇交于一点，且于R7的轴线的延长线上，左右两条支链相当于同轴转动，此时，关节可以转动。当主动转动副R2驱动时，改变转动副R3的轴线，此时的R1，R3，R6三个转动副的轴线不再汇交，即左右两条支链不再同轴，由于约束力的变化，主动力做功的改变，导致关节处于锁紧状态。

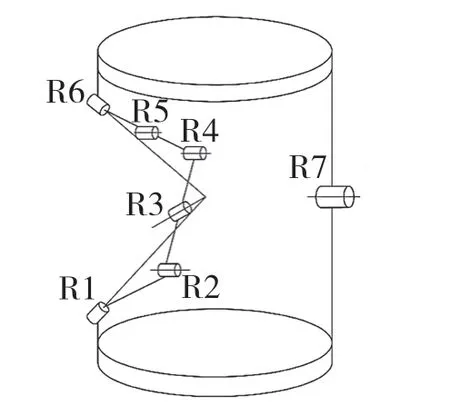
图2 关节结构CAD 简图Fig.2 CAD sketch of joint structure

2 机构的可动性研究

为了便于问题分析，建立坐标系 如图3所示。其中，坐标原点o 为R1和R6轴线的交点，x 轴沿着R3轴线的方向，y 轴沿着R7轴线方向，z 轴遵循右手定则。

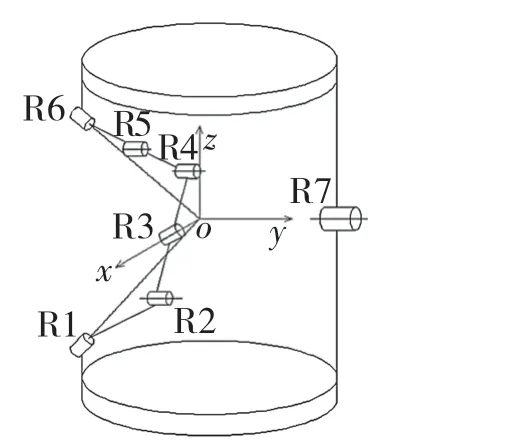
图3 机构坐标示意图Fig.3 Schematic diagram of mechanism coordinates

在此设R1，R3，R6三个转动副的轴线空间汇交于一点时为姿态1，当R1，R3，R6三个转动副的轴线空间不再汇交于一点时，为姿态2。在姿态1 时，关节左侧支链的运动螺旋系可表示为

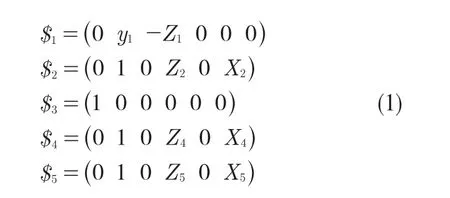
动平台的速度可表示为

同时可以看到，上述6个旋量的Plücker坐标，第5 列元素均为0，该旋量集的秩为5。左侧支链存在的6 个旋量线性相关[6]，必有一组非全为0 的使得动平台的速度有如下关系：

机构可动的充要条件是其支链上的所有旋量线性相关[7]，其中R2可由R1，R3，R4，R5，R6线性表示。左侧支链的运动不会引起动平台的运动。

由式（1）可知，左侧分支的运动螺旋系为5 系，该分支对动平台的运动提供一个约束螺旋为

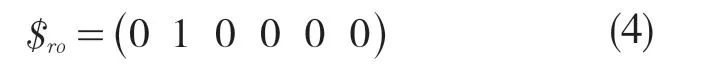
式（4）表明，左侧支链的约束螺旋系仅包含沿y 轴方向的约束力，即该分支限制了动平台沿y 轴移动的自由度。

右侧分支提供固定约束，运动螺旋系可表示为

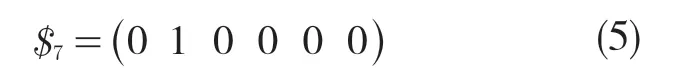
该分支的运动螺旋系为1 系，那么约束螺旋系为5 系。由互易积理论有

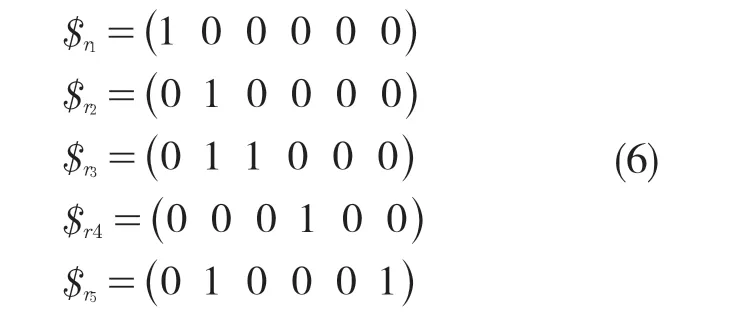
式（6）表明，右侧支链的约束螺旋系包含3 个轴线互相垂直的约束力和两个分别垂直于xoy 面和yoz 面的约束力偶，即该分支约束了动平台空间内的3 个移动自由度和两个垂直于xoy面和yoz 面的转动自由度。并联机构的自由度可利用修正Grubler-Kutzbach 公式进行计算[8]，即

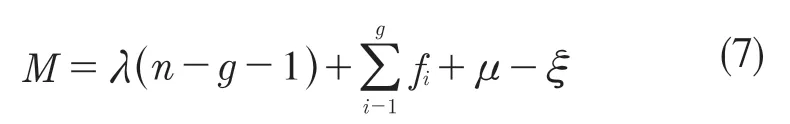
式中：M——机构的自由度数；λ——机构的阶数；n——机构的构件总数；g——机构运动副总数；fi——第i 个运动副的自由度数；μ——冗余约束数；ξ——局部自由度数。

对于图3 所示机构，姿态1 时：λ=6，n=7，g=7，，μ=0，ξ=0，代入式（7）得该机构自由度M=1。

动平台的约束为两条支链的交集，在姿态1时，机构的动平台仅含有一个沿y 轴转动的自由度；姿态2 时，即在R2的驱动后，R3的轴线发生变化，此时，R1的轴线、R3的轴线和R6的轴线不再汇交。R3对应的运动螺旋可表示为

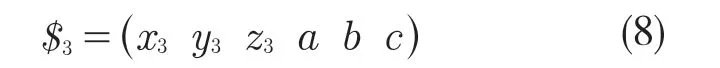
此时，提供固定约束的R7与R1，R3，R4，R5，R6线性无关，左侧支链不参与运动，故当R2和R7同时驱动时，即R3转动副的轴线发生改变时，关节不满足转动要求，可达到有效锁紧能力。

3 ADAMS 仿真

在ADAMS 中建立模型，上下关节均采用相同圆柱体简化，其中下关节用固定副固定在大地上，各连杆之间通过转动副连接，各连杆之间的几何位置关系跟上文表述一致。其中，模型中的细圆杆为各转动副的轴线方向，设置仿真时间为3 s；R2主动副对应的驱动函数：STEP（time，0，0d，2，0d）-STEP（time，2，0d，3，30d）；R7主动副对应的驱动函数为：30.0d×time。具体参数见表1。

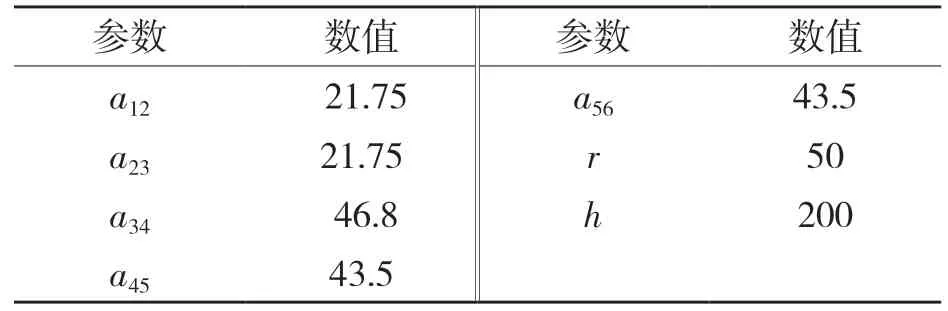
表1 机构的结构参数Tab.1 Structural parameters of mechanism

表1 中：aij——第i 个转动副与第j 个转动副之间连杆的长度；r——上、下关节的半径；h——上、下关节之间的高度。

在位姿1，即R1，R3，R6的转动副轴线汇交于一点时，仅有R7主动副驱动时，关节只含有一个绕y 轴的转动自由度，此处只考虑上关节在x 轴方向的运动，分别测量了质心点在x 轴方向的运动情况，如图4、图5 所示。

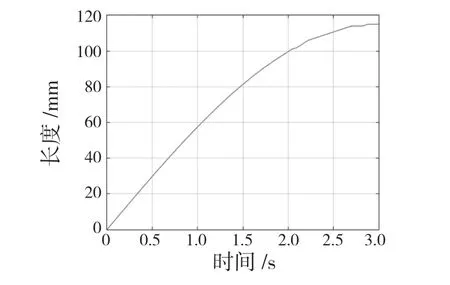
图4 质心点在x 轴方向的位移曲线Fig.4 Displacement curve of centroid point in x-axis direction

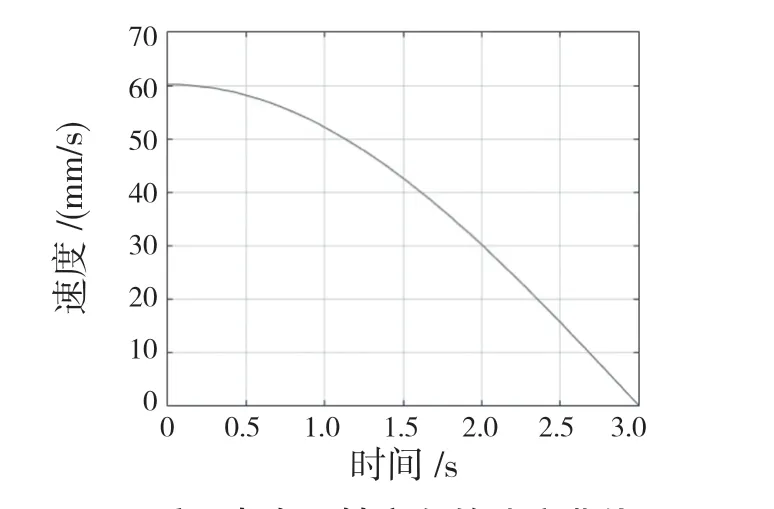
图5 质心点在x 轴方向的速度曲线Fig.5 Velocity curve of centroid point in x-axis direction

当R2和R7主动副共同驱动时，即0～2 s 时间内，第3 转动副的轴线未改变，2 s 后，第3转动副的轴线开始发生变化。上关节质心点在0～3 s 内的运动情况如图6、图7 所示

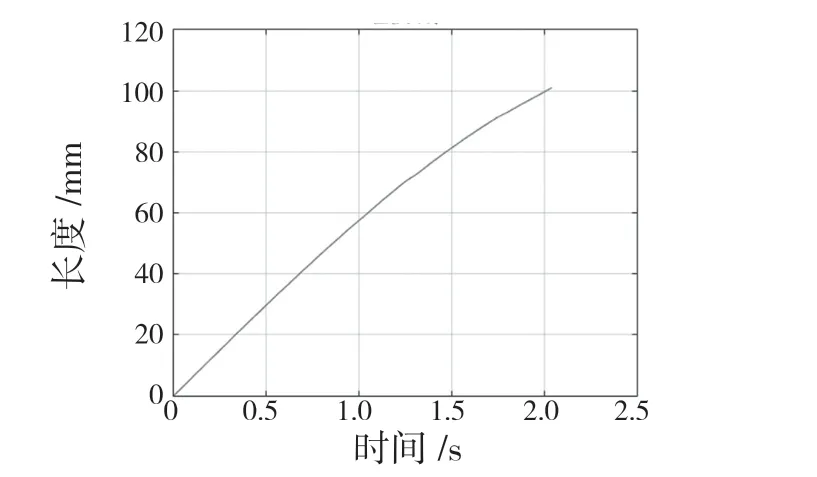
图6 质心点在x 轴方向的位移曲线Fig.6 Displacement curve of centroid point in x-axis direction

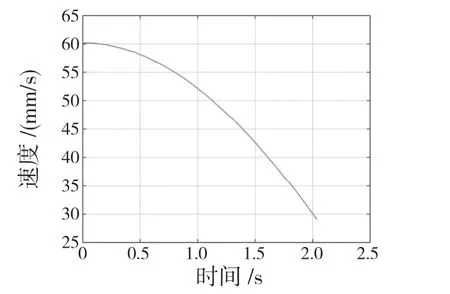
图7 质心点在x 轴方向的速度曲线Fig.7 Velocity curve of centroid point in x-axis direction

从上述的测量曲线可以发现，在只有R7驱动时，整个关节可以转动到仿真结束，但是在R2和R7共同驱动时，在2 s 后仿真便结束。实质上在0～2 s 时，主动副R2在0～2 s 不起作用，等价于R7主动副单独驱动；在2～3 s 时，属于R2和R7共同驱动。R2主动副一旦驱动，R3的轴线将发生变化，此时关节的位姿从姿态1 转变到位姿2，所以此时机构不可动，仿真结束。ADAMS 运动学仿真与上文中的理论分析完全吻合，该关节可以实现相邻关节之间的有效锁紧。

4 实验验证

建立三维模型如图1 所示，并打印分析。如图8 所示，下关节固定在实验平台上，在模型的右支链与上关节连接处系细绳，通过绳子系住不同质量的砝码（分别为30，40，50 g）。

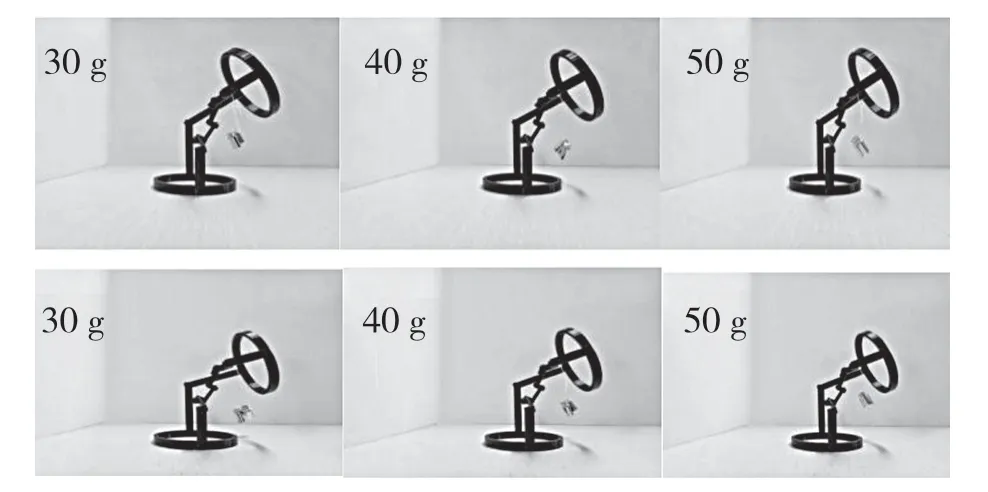
图8 姿态2 不同转角下关节的负载实验Fig.8 Joint load experiment at different rotation angles in posture 2

让砝码在重力作用下自然下垂，进行负重实验，在两处不同的锁紧状态下（135°和120°）均可承受一定的载荷，可以证明关节能够实现不同转角下的有效锁紧。

5 结论

本文中提出了一种可进行有效锁紧的机械臂关节。通过螺旋理论对关节的两种姿态进行分析，线性相关性分析关节的可动性，确定关节的转动与锁死两种状态，建立ADAMS 模型进行运动学仿真。最终对3D 打印件在锁死状态下进行负重实验，可以进行少重量的负重，证明该关节机构可以实现关节的有效锁紧。