基于相依结构的保险公司动态财务分析

张崇林，吕 端

（1.中国人民保险集团股份有限公司，北京100031；2.中国财政科学研究院，北京100142）

一、引言

当前，中国的保险业正处于快速发展的阶段。为了建立一套既与国际接轨又与我国保险发展相适应的偿付能力体系，原中国保险监督委员会于2013年5月初颁布了《中国第二代偿付能力监管制度体系整体框架》，框架明确了保险监管的原则与方向，对保险公司的稳健性经营提出了更高的要求。报告显示，当前保险业偿付能力评估方法已由以定性分析为主转向以定性和定量分析相结合。为了适应保险公司量化分析不同风险之间的关系以实现经营的稳定性和满足偿付能力的要求，由美国财险精算师协会所倡导的动态财务分析（Dynamic Financial Analysis，DFA）方法被国际上的保险机构广泛采用。DFA 是一种金融建模方法，其基本原理是在不同情景下，通过对内部及外部变量的设定来分析和预测保险公司的财务状况和偿付能力，为管理者提供科学的决策依据［1］。DFA方法的基本步骤包括：构建经济情景模型，确定模型参数和输出并分析模型结果。在构建经济情景模型阶段主要通过对保险公司所面临的现实经营环境，特别是对宏观经济与金融市场的特征进行合理的情景模拟以反映公司的潜在风险；随后需要确定经济情景模型中的参数，根据保险公司实际经营情况及经济运行环境，主要对模型中诸如理赔和投资收益等随机因素进行设定；最后，通过DFA模型可以输出关于保险公司财务状况的各种相关信息，进而对公司的业务经营状况和运行风险进行分析和预测［2］［3］。

目前，DFA方法已经成为保险业，特别是财产保险公司实施全面风险管理的有效工具。学者们在研究DFA 模型时，通常会对保险公司可能面临的风险因素进行模拟，主要包括市场风险、经营风险、资产风险和负债风险，以便对公司现在的财务状况有所掌握并对未来的财务状况做出相应的预测。在DFA 模型框架下，Blum 等［4］主要研究了汇率波动对保险公司再保险决策的影响。D'Arcy 和Gorvett［5］利用DFA模型确定对财险公司最优的业务增长比率并且考虑利率风险对承保收益和投资收益的影响。Eling 和Toplek［6］通过DFA 模型分析再保险业务以及风险之间的非线性关系对保险公司偿付能力的影响。

本文运用Copula 来描述这种相关性。自Embrechts等［7］将Copula引入量化风险管理领域以来，Copula 理论已经成为研究金融市场资产风险和负债风险相依关系的有效工具。例如：陈珏宇等［8］运用时变的Copula-GARCH 模型对中美股票市场动态相关性进行实证检验。为准确地度量包含有多项金融资产组合的风险，范国斌等［9］提出使用正则藤Copula对多项资产之间的非线性相依结构进行建模。张连增和胡祥［10］比较了在相关性分析中用参数方法和半参数方法估计Copula函数的有效性。

本文研究的创新之处在于：首先，在DFA模型架构下，通过使用不同的Copula 函数来描述资产风险之间以及负债风险之间的全面相依关系并研究相依系数的变化对保险公司财务状况的影响。通过分析，提出相应的措施来消除这些影响以提高保险公司的偿付能力。其次，鉴于国内关于DFA的研究大多基于定性分析的层面［2］［3］［11］，本文结合国内外关于DFA模型研究的现状，通过建立模型、设置参数和运用随机模拟的方法，从定量分析的角度，探讨DFA在保险公司风险管理上的应用。

文章的结构安排如下：第二节主要建立DFA模型，介绍几类Copula 函数及其性质并提出几类常见的风险函数作为度量保险公司风险和收益的指标。第三节对DFA模型中参数进行设定并通过随机模型得出相应的数据以分析保险公司的财务状况。第四节为结论与展望。

二、模型建立

（一）DFA模型

首先给出DFA模型的基本框架。考虑保险公司在T时期内的财务状况，当t∈{1,...T}时，设ECt为保险公司在第t时期末的权益资本。不同时期之间的权益资本满足如下的关系：

其中，Et表示在第t时期内保险公司的收益。设保险公司的当期收益由投资收益It和承保收益Ut两部分组成。记税率为tr，那么：

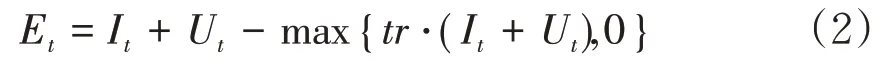
假定保险公司在进行投资决策时，将资金投向两种风险收益不同的市场。在期末，风险较高市场的收益率为r1t，投资的权重为αt-1；风险较低市场的收益率为r2t，权重为1-αt-1。特别地，假定r1t和r2t都服从正态分布。因此，保险公司在第t期末的投资收益率为：

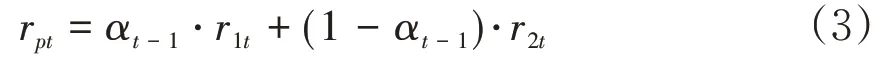
从而投资收益为：

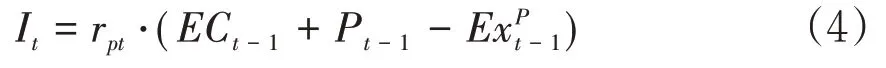
其中，Pt-1为上一期的保费收入，为上一期的预付成本。

显然，保险公司承保相关业务之后会产生理赔并产生理赔费用，不妨将其分别记为Ct和ExCt。如果理赔和理赔费用都在期末支付而预付成本在期初支付，则承保收益可以表示为：

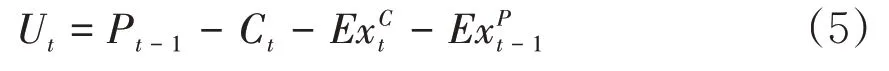
下面对式（5）右边的各个变量进行进一步说明。设t时期的保费由初始保费和承保周期决定。本文借鉴胡三明和吴洪［12］的结论，即认为承保利润率服从二阶自回归过程（εt为随机干扰项）。那么t时期的承保利润指标满足如下的关系：

设初始保费为P0，假设当期的保费由初始保费和当期承保利润率所决定，即：

其中，P0为初始保费，βt为t时期公司保费收入在整个市场所占的份额。设保险公司的理赔总额由巨灾损失（catastrophic loss）和非巨灾损失（non-catastrophic loss）组成，即在时刻t，有：

其中巨灾损失理赔总额由两种业务组成，每种业务都通过复合泊松过程来刻画，且索赔次数服从泊松分布而索赔额服从帕累托分布；非巨灾损失理赔总额则由对数正态分布来刻画①。

假设预付成本由公司业务在整个市场所占份额的线性比例部分和市场份额变动的非线性比例部分所构成，即：

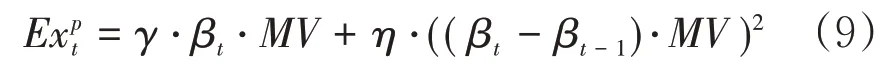
其中，γ和η分别为线性比例和非线性比例，MV为整个市场容量（market volume）。对于理赔费用，假定其占理赔的比重为δ，即=δCt。在下一节的随机模拟与分析中，我们需要对DFA 模型中的各个参数进行赋值。

（二）Copula函数

上文已通过正态分布和帕累托分布分别对保险公司的投资收益率和巨灾损失索赔额进行了建模。为了进一步分析，通过Copula 函数描述变量之间的相关性。

对于随机变量X1和X2，假设它们的联合分布函数为F，则对任意的x1＞0，x2＞0，Copula 函数C满足：

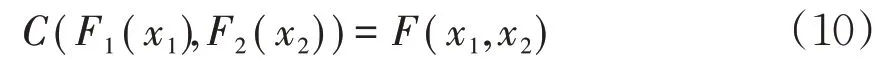
其中F1和F2分别为X1和X2的分布函数。由式（10）可知，随机变量的联合分布函数都由边际分布函数和Copula函数所确定。

Copula 函数类有很多，不同形式的Copula 函数由于刻画的相依关系不同会导致不同的分析结果［13］1-47。传统的线性相关系数只能描述变量之间的线性相关性，由Copula 函数可以定义更多能够描述非线性关系的相关性系数，如Kendall 秩相关系数τ和Spearman 相关系数ρ［14］157-225。本文主要使用Kendall秩相关系数τ描述非线性相关性。

（三）风险与收益度量指标

基于以上的建模，我们的目的是通过DFA 模型来分析保险公司的财务风险，特别是在公司的承保业务和投资收益存在相依关系风险时。本节提出几类常见的风险函数作为度量保险公司风险和收益的指标。

记期望净收益为：

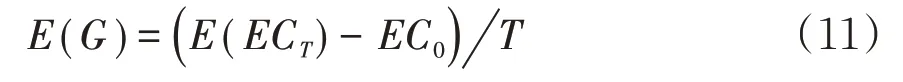
其中E(ECT)表示在T时期的期望权益资本。E(G)可以衡量保险公司收益水平。由于DFA 方法的基础是随机模拟，为了度量由随机效应导致的波动风险，选用净收益的标准差，记为σ(G)，则：

其中σ(ECT)为T时期的权益资本的标准差。为了从概率的角度反映保险公司的偿付能力水平，使用破产概率这一指标。破产概率（Ruin Probability，RP）表示公司盈余水平首次达到零点以下的概率，其定义：

其中τ=inf{t＞0,t=1,2,...,T:ECt＜0}为保险公司的破产时刻。保险公司“破产”，破产概率无法给出在破产时刻公司的赤字水平。因此，本文还使用保单预期赤字（Expected Policyholder Deficit，EPD）作为进一步衡量保险公司财务状况及偿付能力的指标，其定义为：

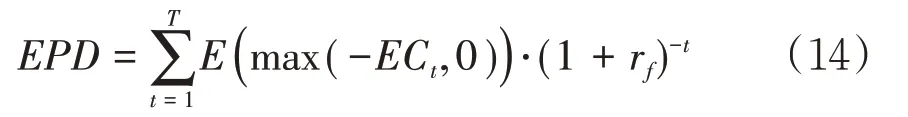
其中rf为无风险收益率。

为了评价保险公司的投资绩效，使用夏普指数（Sharp Ratio）作为标准化指标。夏普指数反映了净收益的期望和波动率之间的关系，不妨将其记为SRσ，则：

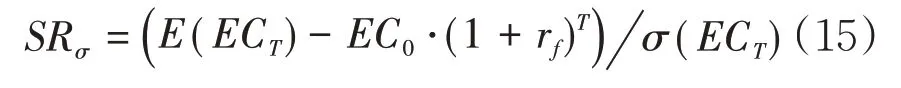
结合式（13）和式（14），本文选择基于破产概率和保单预期赤字的夏普指数作为保险公司绩效评价的指标，分别记其为SRRP和SREPD，则：

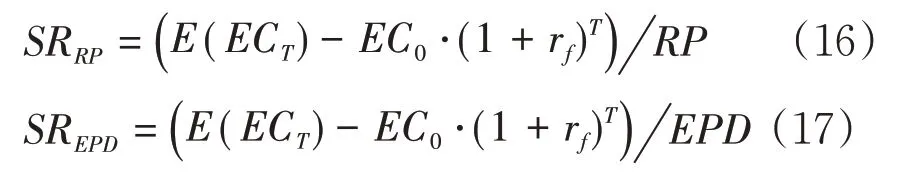
当对DFA 模型中的参数进行赋值后，通过随机模拟，可以计算得出由式（11）-（17）所确定的度量指标的具体数值。

三、随机模拟与分析

（一）参数设定

本节主要通过随机模拟对某财产保险公司财务风险进行动态分析。在随机模拟之前需要对DFA模型的基本参数进行设定。由于无法特定选取某个具体的保险公司的经营数据，所以只能粗略地进行仿真。但是在参数设定时仍然尽可能使其接近实际情况。

相比于传统的人寿保险，财产保险的经营周期相对较短。令周期为5年，即T=5。设整个市场容量为MV=1000万，该保险公司在初始时刻t=0时所占的比重为β0=0.2，随后几个时期呈现一定的变化：即β1=0.205，β2=0.21，β3=0.215，β4=0.21。承保利润率服从二阶自回归过程且参数分别为α0=0.638，α1=0.817，α2=-0.304。对于预付成本，参见式（9），令γ=0.05，η=0.001，同时令税率tr=0.25。

前文已假定投资收益率r1t和r2t都服从正态分布。进一步，设高风险收益率r1t的期望为10%，标准差为20%；低风险收益率r2t的期望和标准差都为5%。假定保险公司资金投向高风险市场的比重为α0=0.4。最后，令无风险收益率为rf=3%。

对于保险公司的承保业务，设非巨灾风险服从对数正态分布，其中期望损失为149 万，标准差为7.43 万；设巨灾风险包含两种业务，皆由复合泊松过程来刻画。其中索赔次数都服从参数为λ=1.2的泊松分布，即两种业务在每一个时期内平均都发生1.2 次。每种业务的索赔额都服从帕累托分布，其中业务一的均值和标准差分别为10 万和11.18万；业务二的均值和标准差分别为7.14 万和7.67万。最后，假定理赔费用占理赔的比重为δ=0.05。

（二）随机模拟

通过R软件，进行重复50000次的Monte Carlo随机模拟实验。

假定高风险与低风险投资收益率之间的Kendall 秩相关系数和两种巨灾风险的索赔额之间的Kendall 秩相关系数相同，且分别取值为0，0.25 和0.75。首先，分析由Kendall 秩相关系数τ(θ)的变化对保险公司的财务状况的影响。当τ(θ)=0时，公司的期望净收益最大，净收益的标准差最小并且破产概率最小；随着正相关性的增强，即当τ(θ)=0.25 或τ(θ)=0.75 时，无论在何种Copula 条件下，公司的期望净收益都在变小，而净收益的标准差和破产概率都在变大。在相同Copula 函数下比较，作为反映保险公司财务状况及偿付能力的指标保单预期赤字也随着相依关系的增强而增加。

在相同的Kendall 秩相关系数条件下，当τ(θ)由0.25 变为0.75，即从弱正相关到强正相关时，基于不同的Copula函数所得出的风险和收益指标大体趋同。然而，随着正相关性的增强，相比于期望净收益和净收益的标准差，破产概率和保单预期赤字变化更显著。

以上的分析表明，与相互独立相比，当投资收益率以及索赔额之间存在正相关性时，保险公司的预期收益会减小，而经营的风险会增加，并且这些正相关性既会增大保险公司破产的风险又会降低公司的偿付能力。当投资收益率以及索赔额之间的正相关性增强时，通过不同的Copula 函数都表明，公司的期望净收益减小，而净收益的标准差、破产概率和保单预期赤字增大，并且破产概率和保单预期赤字变化的幅度更大。

进一步假定投资收益率以及索赔额之间存在负相关性并分析其对保险公司财务状况的影响。首先，无论是在何种Copula函数下，当高风险与低风险投资收益率之间的Kendall秩相关系数由0.25变为-0.25 或者两种巨灾风险的索赔额之间的Kendall 秩相关系数由0.75 变为-0.75 时，保险公司的期望净收益在增大，而净收益的标准差则在减小。同时，随着相依关系由正变负，破产概率和保单预期赤字减小幅度显著。

分析表明，与正相关性相比，无论是在投资收益率之间还是在索赔额之间引入负相依关系，保险公司的预期收益都在增大而经营的风险在减小，并且会导致保险公司破产风险减小，从而提高公司的偿付能力。

为了进一步证实该结论，在Gaussian Copula和Frank Copula 条件下，类似地，如果投资收益率以及索赔额之间的Kendall 秩相关系数由正变负，保险公司的预期收益增大，预期收益的波动、破产概率和保单预期赤字都在减小。

如果高风险与低风险投资收益率之间存在正相关性，表明收益率同增或同减，即两者变化趋势相同。显然这有悖于投资组合理论中的分散投资的策略。面对投资收益和风险的不确定性，选择存在负相关性的投资组合有助于提高保险公司的财务状况和偿付能力。

对于巨灾风险索赔额之间的相关性，随机模拟的结论表明：降低索赔额之间的相依关系会改善保险公司的收益和风险水平。在很多情况下，风险之间会存在某种相关性。例如在年金产品中，保单组合中被保险人的剩余寿命是相关的。保险公司在承保业务时，需要注意到承保风险之间的正相关性通常会增加公司的财务风险，降低偿付能力。虽然在实际经营中公司无法拒绝承保此类风险，但是适当地增加此类业务的保费和提高责任准备金水平都是有效的风险防范措施。

四、结论与展望

本文主要在DFA 模型框架下，研究分析投资收益率以及索赔额之间的相依关系对保险公司财务状况的影响。通过随机模拟的方法，基于常见的风险与收益度量指标，得出如下的结论：首先，随着投资收益率之间相依关系的增强，保险公司的预期收益在增大而经营风险在减小，并且导致保险公司破产风险减小，从而提高公司的偿付能力。保险公司在进行投资决策时，应充分采用风险分散的策略，即选择收益率之间存在负相关性的投资组合以消除收益率“趋同”对保险公司的财务状况和偿付能力的影响。其次，索赔额之间的正相依关系也会对保险公司带来负面影响。越来越多的经验表明，传统的保险精算方法中的独立性假设不再成立，不同业务的索赔额之间通常存在相关性。为了防范此类风险对保险公司财务及偿付能力的影响，有必要提高相应的保费和准备金水平。