基于图论的矩阵模型在管网水力计算的应用

吕思凯 李根

（1 南京科远智慧科技集团股份有限公司 江苏南京 211102 2 江苏省热工过程智能控制重点实验室 江苏南京 211102）

1 供热管网水力计算的重要性

管网是输送物料的主要设施，是工业领域物料流通的“血管”。其中热水供热管网尤其具有代表性，它连接着热源与众多用户，需要将热能有效、合理地输送与分配。供热管网具有延伸距离长、覆盖范围广、分支结构复杂等特点。

流体在供热管网中流动时，由于原有热用户的使用负荷不断变动、新增热用户数量不断增加，使某些管段的流量分配值无法很好地匹配设计要求，严重影响热网的可用性与经济性，同时也给热源的正常生产运行产生不良的影响。为了使供热管网更好地适应不同的相关因素的变化，始终保持良好的输送质量，就需要对供热管网进行水力工况分析，以判断整个管网的可靠性与安全性。

由于供热管网繁杂的结构特征，只依靠手工计算已经难以达到模拟计算的要求。随着计算机技术及管网计算理论的快速发展，运用计算机进行供热管网的水力计算模拟成为可能。以计算机为硬件基础，以可靠的计算理论为指导思想，对大型供热管网进行方案优化、可靠性推断、经济性分析对于国民经济的可持续性发展、实现节能环保的目标具有十分重要的意义。

2 图论在管网系统中的应用

图论是数学的1 个分支，它以图为研究对象。图论中的图是由多个确定的点及连接两点的线所组成的结构，这种图形通常用来表达某些对象之间某种确定的关联，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系［1］。

20 世纪70 年代，图论研究随着计算机技术的迭代更新，在各种领域的运用都得到了迅速的发展。将供热管网抽象成各节点和管段的集合，利用图论和矩阵方程将管网的结构关系数字化，是目前管网流体分析不可或缺的手段。在图论中运用基尔霍夫定律研究流体管网就是1 个非常典型的应用。

在图论中，管网的结构可以简化成点与线所组成的线图，某管网的模型如图1 所示。

图1 某管网模型

图论的基本概念如下。

（1）节点：在流体网络中，节点即管段的交点。有些节点只有介质流入或流出，称之为边界点。有些节点既有介质流入、也有介质流出，称之为中间点。所有节点所组成的集合称为V，图1 中的V={v1，v2，v3，v4，v5，v6}，一般用N 表示节点数量。

（2）支路：各个节点之间的管段称为分支，所有分支所组成的集合称为E，图1 中的E={e1，e2，e3，e4，e5，e6，e7}，一般用M 表示支路数量。

（3）关联矩阵：表示管网中各个节点流向与各支路拓扑关系，用N×M 阶矩阵A=aij表示，其中i=1，2，…N，j=1，2…M［2］。

由图1 可得到矩阵A。由于矩阵A 的秩是5，矩阵A 所对应的方程组中有1 个方程是多余的，因此，在进行运算时，需要去掉1 个行向量，得到满秩矩阵，称之为降阶关联矩阵Alow。

3 模型计算的相关定理

3.1 基尔霍夫电流定律

基尔霍夫电流定律表明：所有流入某节点的电流之和与所有流出这个节点的电流之和相等。或者，若流入某节点的电流为正值，流出这节点的电流为负值，则所有关联这节点的电流的代数和为0［3］。

基尔霍夫电流定律同样适用于管网流量的计算，以列向量q 表示各管段流量，以列向量Qlow表示各节点的净流出量，用降阶关联矩阵Alow左乘流量向量q 可得到节点流量Qlow，此方程称为节点流量方程，如式（1）～（3）。

3.2 基尔霍夫电压定律

基尔霍夫电压定律表明：在任何一个闭合的回路中，各部件上的电压降低值的代数和与电动势的代数和相等，即从某点开始围绕回路1 圈后回到该点，各段电压的代数和恒等于0，即∑U=0［3］。

与基尔霍夫电流定律相对应的是，基尔霍夫电压定律同样适用于管网压力降的计算，以列向量Hlow表示各节点压力，以列向量ΔH 表示各管段的压降，用降阶关联矩的转置矩阵AlowT左乘流量向量Hlow可得到节点流量ΔH，此方程称为管段能量方程，如式（4）～（6）。

3.3 管段压降方程

管段中流体的阻力即单位质量的流体的机械能的损失，产生机械能损失的原因是流体内部的黏性耗散。流体在直管段中的流动因摩擦和流出生成的涡流导致的机械能损失称为直管阻力；流体通过各种管道附件因流通截面积变化、流动方向变化形成的大量旋涡而导致的机械能损失称为局部阻力；因此，管道中流体的压降等于直段的阻力与局部阻力的总和［4］，如式（7）～（9）。

式中：hf1为直管阻力；λ 为摩擦因子；L 为管段长度；D 为管道内径；u 为流体平均流速；hf2为局部阻力；∑Ki为所有管件的管道阻力系数，与管件的结构特性有关。

将hf1、hf2相加后整理可得ΔH=S｜q｜q，其中ρ 为流体密度，在管网中实际水流方向与管段的取向不一致时，流量q 取绝对值可以算出压力降为负，保证运算的一致性，如式（10）。

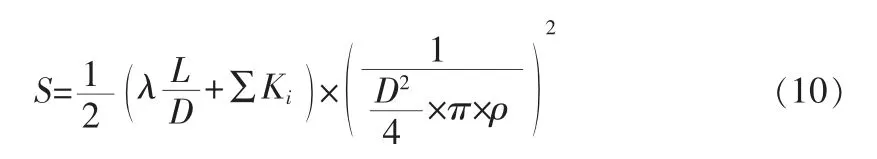
4 供热管网水力计算模型的建立

将上述3 个方程联立，采用节点方程法求解。对于已知的N 个节点，M 条管段的管网，结合霍尔基夫定律及供热管网水力计算的基本理论，可得到如下通用的供热管网数学模型，如式（11）。

式中：Alow为（N-1）×M 的降阶关联矩阵；AlowT为降阶关联矩阵的转置矩阵；Qlow为节点流量列向量，Qlow=（Q1，Q2，Q3，…QN-1）T；q为管段流量列向量，q=（q1，q2，q3，…qM）T；ΔH 为管段压降向量，ΔH=（ΔH1，ΔH2，ΔH3，…ΔHM）T；Hlow为节点压力列向 量，Hlow=（H1，H2，H3，…HN-1）T，Hi为各节点相对于参考节点的压力，Pa；S 为M×M 阶阻力系数对角矩阵，S=diag（S1，S2，S3，…SM）；｜q｜为M×M 阶管道流量绝对值对角矩阵，｜q｜=diag（｜q｜1，｜q｜2，｜q｜3，…｜q｜M）；Z为管段分支中两节点的势能差向量，Z=（Z1，Z2，H3，…HM）T；HP为管段中水泵的扬程向量，HP=（HP1，HP2，HP3，…HPM）T。

解节点方程时，节点流量连续性方程是以管道中的流量值为自变量，需要将其转化成线性表达式，并且以节点压力为自变量［5］。而在求解过程中，初始的节点压力假设值肯定能满足能量方程，但由此计算得出的管道流量通常不能满足节点的流量方程。因此，在计算过程中，需要不断迭代，修改节点压力的数值，直至管道的流量可以达到设定的允许误差范围之内，认为满足节点流量连续性方程。

5 结语

本文将图论及电工学中的基尔霍夫定律运用到供热管网的流体模拟计算中，建立了供热管网水力计算的通用计算模型。在求解过程中，介质密度、动力粘度、普朗特数都会随着管线的阻力变化，需要通过计算结果反过来修正计算输入值，使输入值与计算结果的误差降到设定值，模型所联立的方程组利用计算机编程来实现迭代求解。