飞机整体结构件的“加工变形-疲劳寿命”多目标结构优化方法

秦国华，郭翊翔，王华敏，侯源君，娄维达

(南昌航空大学航空制造工程学院，南昌330063)

现代飞机飞行性能的不断改善对零件的轻量化、长寿命等指标提出了越来越高的要求，因此，在现代飞机的结构设计中大量采用了整体结构。整体结构件与传统的结构件相比具有很多优点，例如重量轻、可靠性高、装配效率高等[1]。但是，整体结构件精度要求高、结构复杂、壁薄等特点，对现代加工技术提出了更为严格的要求。尤其是铝合金航空整体结构件一般由铝合金厚板去除90%～95%的材料而获得[2]，因此在加工要求很高的航空结构件的制造过程中，加工变形是其面临的一个重要难题[3]。

在零件的数控加工过程中，随着加工的进行，材料不断被去除，毛坯内部的初始残余应力不断被释放，破坏了毛坯内残余应力的平衡，最终导致零件的变形，因此研究如何通过毛坯内部的初始残余应力求得零件的加工变形是很有必要的。Cerutti等[4]以层剥法测量得到毛坯中的初始残余应力，通过在Forge 有限元软件中加入布朗运算，实现了加工变形的分析与预测。Fu 等[5]提出了两种更准确的计算初始残余应力的分段计算方法，并通过有限元仿真和加工实验验证了其有效性，并指出只考虑初始残余应力能够获得较高的加工变形预测精度。Gao等[6]提出了一种薄壁件加工变形的半解析预测模型，并在此基础上研究了初始残余应力对加工变形的影响，发现减小毛坯顶部和长度方向上的应力更有利于减小变形，而且当残余应力在厚度方向沿中平面对称分布时，最终加工变形基本上由毛坯表面下一定厚度内的残余应力决定。Ye等[7]探究了加工位置对工件变形的影响，并提出了变形最小的优化模型和相应的步长递减算法，该方法得到的最优加工位置可使加工变形减少99%左右。

在航空器的服役过程中，由于发动机开车、机动飞行、大气紊流、抖振等[8]因素，航空器内部的整体结构件也承受着大量的循环载荷。在外部循环载荷的作用下，零件内部的缺陷或裂纹可能进一步扩展甚至引起结构的失效。因此，设计零件时，对其进行疲劳分析以保证结构件的疲劳寿命是必要的。Chen 等[9]研究了一种基于DSM参数的不同疲劳载荷下的累积损伤方法，与包括Miner 方法在内的其他模型相比，其预测的疲劳寿命更为准确。Miikka 等[10]提出了一种基于层次贝叶斯的疲劳试验数据分析方法，该模型预测的疲劳寿命与实测数据吻合得较好。李钰等[11]通过对飞机失效零部件的分析，拓展了估算复杂连接件的疲劳寿命与裂纹扩展寿命的逐次累计求和算法，该文的寿命估算结果与端口判读结果吻合良好。乔扬等[12]提出了一种基于统计能量理论的结构高频随机振动疲劳寿命计算方法，该方法计算精度高，是高速飞行器强度设计的一种可靠方法。

设计部门依据疲劳寿命等需求设计整体结构件的整体结构形状，而数控加工部门则关心整体结构件的加工变形。在整体结构件的高速铣削过程中，毛坯初始残余应力造成的加工变形，不仅取决于结构件在材料去除后所受到的应力，而且也取决于结构件的结构。为此，针对由7075-T7451铝合金毛坯加工而成的三框梁零件，本文通过对毛坯初始残余应力的等效转换，利用材料力学的弯曲变形公式，建立了残余应力释放导致的加工变形模型。还通过结构件最小疲劳寿命与最大疲劳应力的等效，利用神经网络拟合得到结构件腹板位置与最大疲劳应力(即最小疲劳寿命)之间的方程。最终使用多目标遗传算法，求解得最优的位置，使得加工变形和最大应力最小化。

1 加工变形分析

使用高速切削加工时，毛坯的初始残余应力是影响加工变形的重要因素[13−14]。为了计算梁类整体结构件的加工变形，需要进行残余应力的等效。

1.1 残余应力释放

在图1所示的铝合金预拉伸厚板(即毛坯)内，轧制方向记为X方向，横向方向记为Y方向，厚度方向记为Z方向。由于铝合金厚板沿厚度方向的残余应力值非常小，完全可以忽略不计[15]，也就是说，在同一厚度的平面内，残余应力值相等。因此在自然状态下，铝合金厚板内部的初始残余应力处于自平衡状态，即内部的力和力矩处于自平衡。因此有：

图1 毛坯与零件示意图Fig.1 Diagram of the blank and the workpiece

在加工的过程中，材料不断被去除，毛坯内的残余应力不断被释放。由于残余应力远小于材料的屈服极限，因此可以把毛坯初始残余应力的释放过程视为毛坯的弹性变形过程。

另一方面，由于粗加工阶段毛坯的刚性依然较大，而初始残余应力较小，此时的变形几乎很小。精加工阶段去除材料后，拆卸装夹后产生了加工变形。由此可见，整个加工过程产生的变形可以看作是由于材料在一次性完全去除过程中残余应力释放导致的，而不必考虑具体的加工过程。

如图1所示，将毛坯Ω加工得到的零件记为W，加工时去除的材料记为M。这样，可将M、W分离看待，M从毛坯中去除后，M内部的残余应力也随之消除。因此加工得到的零件的变形可以认为是在自身的残余应力作用下，由于残余应力产生的力和力矩不平衡形成的。零件W在X方向(轧制方向)和Y方向(横向方向)上的载荷分量分别为：

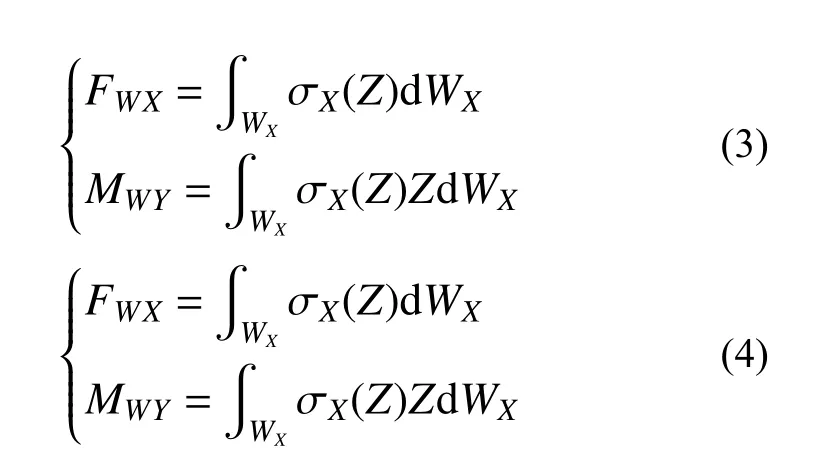
式中：WX、WY分别为零件垂直于X轴、Y轴的截面；FWX、FWY和MWX、MWY别为零件在X方向和Y方向受到的力与力矩。

1.2 变形模型

由式(3)与式(4)可知，施加于零件上的载荷由σX(Z)和σY(Z)同时作用产生，为了便于分析零件的变形，根据广义胡克定律，定义轧制方向上的等效应力σ(Z)如下：

式中，v为零件材料的泊松比。

显然，零件必然因σ(Z)产生的弯矩不平衡而发生变形。按照图1与图2所示建立的坐标系xyz，并记零件在任意位置x处截面Wx的中性层高度为H(x)，则该截面上的弯矩为：

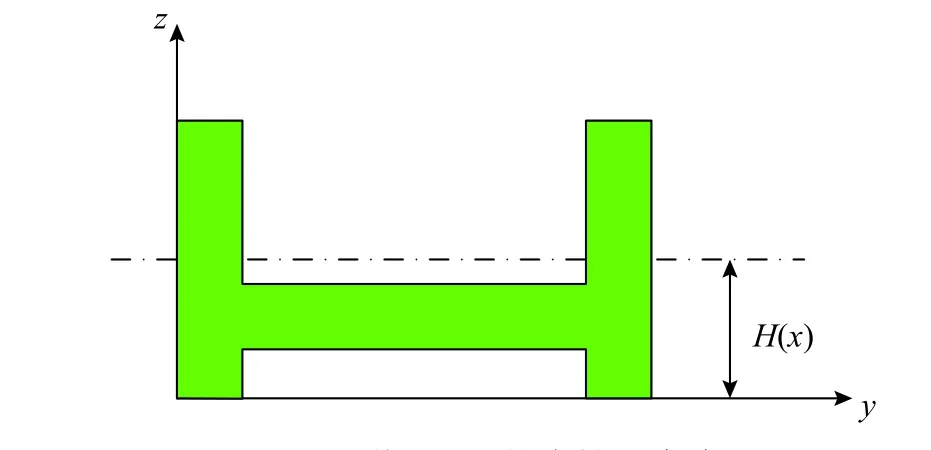
图2 截面Wx 的中性层高度Fig.2 Neutral axis height of the workpiece cross section Wx

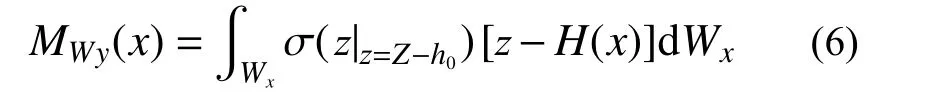
由材料力学可知，任意位置x处由弯矩MWx(x)产生的厚度方向的挠度wz(x)可以表示为：

式中：E为材料的弹性模量；IWy(x)为截面Wx的截面惯性矩。

对式(7)进行两次积分，即可得到任意x处的挠度为：

式中，B、C为待定系数，可由边界条件得出。

图3为某航空三框整体结构件示意图，尺寸为1100 mm×80 mm×30 mm，缘条壁厚均为1.5 mm，腹板厚度为2 mm。选择的毛坯尺寸为1200 mm×120 mm×60 mm，零件底部距离毛坯底部16.5 mm。

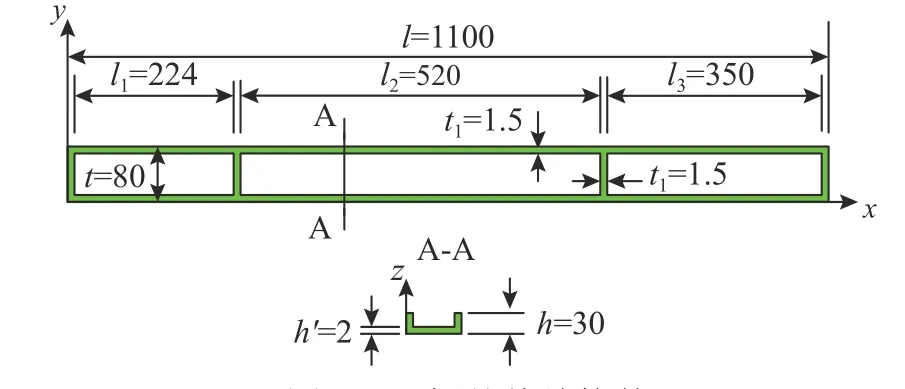
图3 三框整体结构件/mm Fig.3 Three frame monolithic component

材料为航空铝合金7075-T7451，弹性模量为E=71.7 GPa，泊松比为ν=0.33。通过裂纹柔度法得到的毛坯初始残余应力分布曲线如图4所示。

图4 初始残余应力Fig.4 Distribution of initial residual stresses

沿着厚度方向对毛坯进行均匀分层，每层厚度为1.5 mm，共40 层。这样，每层的应力值如表1所示。

表1 每层残余应力值Table 1 Residual stress in each layer

为便于计算，对毛坯内的等效应力进行拟合：

将式(12)代入式(8)，结合梁的挠度和转角的连续性条件(见图5)，可确定梁的变形曲线为：

图5 约束条件Fig.5 Constraint conditions

根据式(13)，可求出最大变形出现在x=549.8 mm处，其值为0.543 mm。

使用有限元方法计算梁的弯曲变形时，有限元模型如图6(a)所示。在ABAQUS中沿厚度方向z对结构件毛坯进行分层，每层厚度为1.5 mm，共分40层。以预定义场的形式分层施加残余应力，即表1中的第12层～第31层，单元类型为C3D20R，计算后的变形云图如图6(b)所示。最大变形出现在x=550 mm 处，其值为0.542 mm。

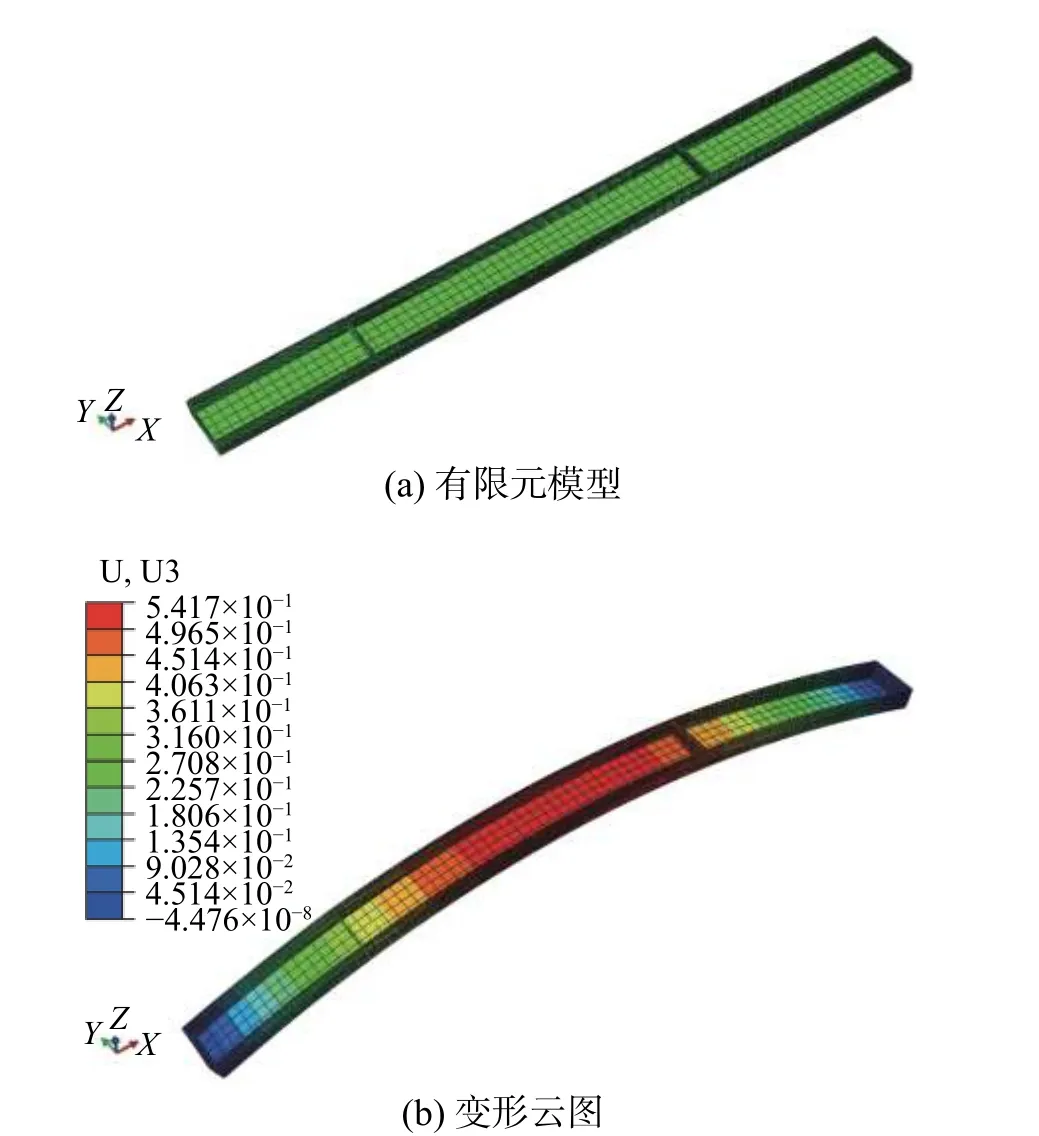
图6 加工变形的有限元分析Fig.6 Finite element analysisof machining deformation

1.3 模型验证

三框整体结构件的实际加工过程中，先采用无应力装夹方式，即用压板顶住毛坯侧面，对毛坯上、下表面进行粗加工至零件的加工位置16.5 mm，如图7所示。

图7 粗加工Fig.7 Rough machining

然后在铣床K211A 3500×1500上，采用应力装夹方式进行装夹。主轴转速为15 000 r/min，铣削外侧缘条时轴向进给仅为0.5 mm，这些参数使得加工过程引入的应力很小，成形后的零件如图8所示。

图8 零件成型Fig.8 Machined workpiece

该零件加工变形的测量在桥式三坐标测量机ADVANTAGE 15.30.10上进行，如图9 所示。主要测量零件腹板中线的变形数据，每隔5 mm 测量一次数据。

图9 测量变形Fig.9 Deformation measurement

图10显示了该零件的加工变形的解析值、仿真值和实验值的比较。解析值得到的最大变形值为0.543 mm，出现在梁的中间位置；仿真值最大值为0.542 mm，同样出现在中间位置；实验值最大值为0.585 mm，出现在中间偏两边约50 mm处。可知，解析值、仿真值结果高度一致，与实验值的差值在合理范围之内。

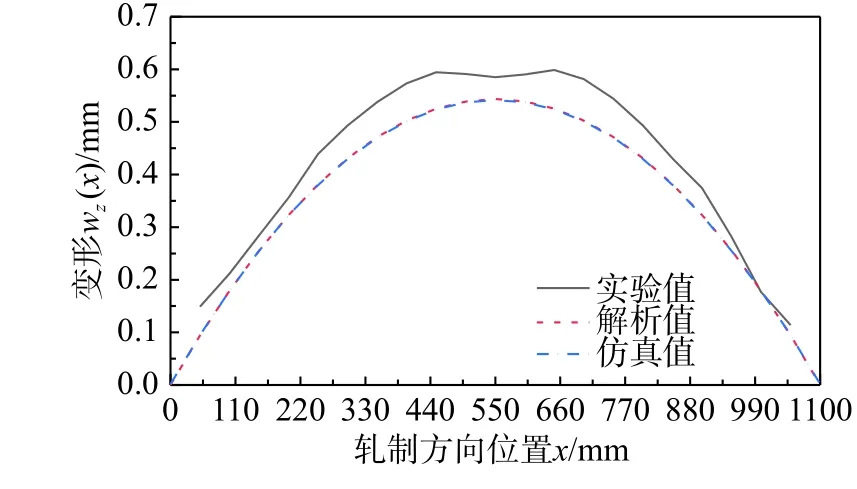
图10 解析值、仿真值和实验值的比较Fig.10 Comparison among the analytical-,simulated-and experimental value

综上所述，要分析零件由于残余应力释放产生的加工变形，可以将毛坯的初始残余应力作为外载荷施加于零件上，通过梁零件的挠曲线方程求解出零件的加工变形。

2 疲劳寿命分析

本文使用名义应力法对三框结构件进行疲劳分析。

2.1 材料的S-N 曲线

名义应力法通过S-N曲线定义对称循环应力的应力范围与循环次数(即疲劳寿命)之间的关系，如图11所示。

为了便于分析，应力范围S与循环次数Nf之间的关系可在双对数坐标系中用直线段描述，如图11所示。因此，S-N曲线可表达为lgS=lgS1+b1lgNf，即：

图11 S-N 曲线Fig.11 S-N curve

式中：S为名义应力范围；Nf为疲劳失效时的寿命；b1为常数(即斜率)；S1为疲劳强度系数。

通常，S-N曲线由试验获得，本文通过式(15)与式(16)的经验公式[16]，利用材料的抗拉极限近似得到：

本文使用的材料为7075-T7451，其抗拉极限为UTS=468.844 MPa。将其代入式(15)与式(16)可得S1=1560.489 MPa，b1=−0.088。

2.2 非对称循环载荷的转化

使用S-N曲线可以计算恒定幅值循环载荷下零件的疲劳寿命，但在实际情况中疲劳载荷非常复杂，难以直接通过S-N曲线预估疲劳寿命。此时，可利用雨流计数法将应力幅值变化的载荷谱分解为若干组简单的恒定幅值循环载荷，每组载荷具有不同的恒定应力幅值、平均应力和循环次数，如图12所示。

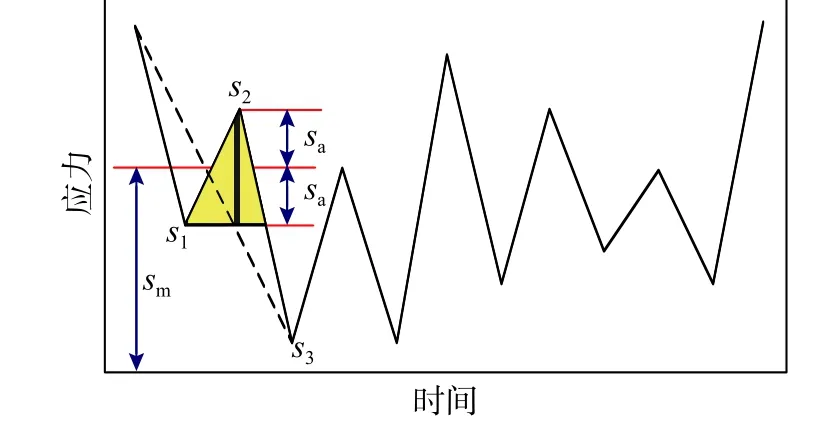
图12 载荷谱的分解Fig.12 Decomposition of load spectrum

S-N曲线通常是由加载对称循环载荷的标准实验得到，而雨流计数法分解得到的载荷不完全是对称循环载荷，并且法向平均应力对零件的疲劳性能有显著影响。就疲劳强度而言，拉伸法向平均应力是有害的，应当考虑非零平均应力的影响。故本文采用Goodman 公式校正平均应力，即：

式中：Sa为应力幅值；Sm为平均应力；Se为等效的对称循环应力幅值。

2.3 Miner 线性损伤累积

载荷谱经过雨流计数及平均应力校正后，被分解成若干组幅值不同的对称循环载荷，代入到材料的S-N曲线中后，可得到每个载荷组对应的疲劳寿命，再通过Miner 线性损伤累积理论就可得到零件在整个载荷谱下的疲劳寿命。

Miner 线性损伤累积理论认为，当式(18)满足时，零件发生疲劳失效。

式中：Nif为材料在第i组疲劳载荷下的疲劳寿命；ni为第i组疲劳载荷的循环次数。

式(18)左边部分的倒数即为零件在载荷谱下的疲劳寿命，即零件可以承受该载荷谱的最大次数。

虽然Miner 线性损伤累积理论没有考虑载荷顺序对损伤累积的影响，但工程上的应用证明它是有效的。

2.4 三框结构件的疲劳寿命分析

三框整体结构件为机翼翼梁的简化结构，其装配关系如图13所示，在空中受载状态类似悬臂梁。

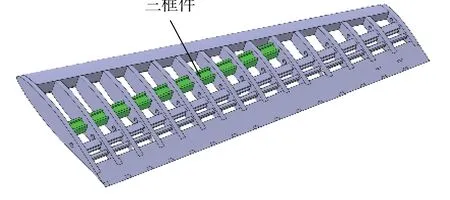
图13 三框整体结构件的装配关系示意图Fig.13 Assembly diagram of three frame monolithic component

这样，在HyperWorks 中对三框整体结构件(见图3)进行疲劳分析时，边界条件应设置为端面约束，疲劳载荷假定为集中力F=100 N，载荷谱为图14 所示的随机循环载荷。

图14 随机载荷谱Fig.14 Random load spectrum

首先对其进行静力分析。采用类型CTETRA、单元密度为2 mm 的单元对三框件进行网格划分，得到283 377个单元和93 344个节点，如图15(a)所示。施加位移约束和力约束后进行计算，结果如图15(b)所示，最大疲劳应力为199.2 MPa，出现在被约束端面。根据图15所示的静力结果，利用名义应力法进行疲劳分析，结果如图16 所示。

图15 静力分析结果Fig.15 Static analysis results

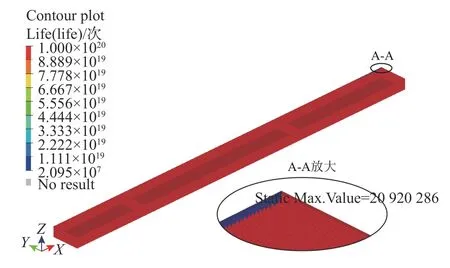
图16 疲劳分析结果Fig.16 Fatigueanalysisresults

由于被约束端面附近应力较大，所以疲劳危险位置出现在该位置。施加随机循环载荷谱时，零件的最小疲劳寿命为2.092×107次。

3 “加工变形-疲劳寿命”的耦合预测模型

三框整体结构件的加工变形，主要由两个方

面的因素决定：一是所受到的残余应力，另一则是零件的结构尺寸。由于腹板不属于装配表面，可以对其位置进行重新设计，进而可以从结构设计上实现加工变形的控制。而且结构的改变也对零件的疲劳寿命产生影响。

三框整体结构件的3个腹板位置分别记为h1、h2、h3，如图17所示。在对变腹板三框梁零件进行疲劳分析时，对于腹板处于任意位置的结构，零件受到的疲劳载荷都是相同的。由名义应力法可知，零件疲劳寿命与应力范围成对数关系。因此，要确定零件的最小疲劳寿命，可先确定零件的最大疲劳应力值。

图17 变腹板三框梁零件/mmFig.17 Threeframe workpiecewith variablewebs

因此，可利用BP神经网络来实现变腹板三框整体结构件最大变形和最大应力的耦合预测。万能近似定理(Universal approximation theorem)表明：一个前馈神经网络，如果具备线性输出层和至少一层具有任何一种“挤压”性质的激活函数的隐藏层，就能以任意精度拟合任意复杂度的函数[17]。故选用的BP神经网络如图18所示，网络结构为3-7-5-2。输入层神经元为3个腹板位置h1、h2、h3。输出层神经元为最大变形y1及最大应力y2。设置2层隐藏层，其神经元数目可按下列经验公式[18]确定，即：

图18 BP 神经网络net 的结构图Fig.18 Structurediagram of BPneural network net

式中：a为输入层神经元个数；d为输出层神经元个数；n0为[1, 10]之间的常数。

由于输入层神经元个数为a=3，输出层神经元个数为d=2，故根据式(19)确定隐藏层的神经元个数分别为b=7和c=5。

确定神经网络样本时，每个腹板位置的采样间隔2 mm，从0 mm 依次取值至28 mm。为减少样本个数，通过正交表选取具有代表性的236组腹板位置进行分析，求得各自的最大加工变形值及最大疲劳应力值，将其作为神经网络的训练集，见附表A。同理，每隔4 mm，从1 mm 依次取值至25 mm，通过正交表另外再选取49组数据，求得各自的最大加工变形值及最大疲劳应力值，将其作为神经网络的测试集，见附表B。

归一化输入样本后，选择具有很快收敛速度的LM算法进行网络训练。训练得到的神经网络，其预测结果如图19所示。其中，y1的训练集均方误差为0.0590，测试集均方误差为0.0492，误差为16.61%；y2的训练集均方误差为15.2520，测试集均方误差为16.9854，误差为11.37%。由于变形值相对较小，故相对应力来说误差较大。但总体上，训练集与测试集均方误差相差较小，可认为网络具有较好的预测能力。

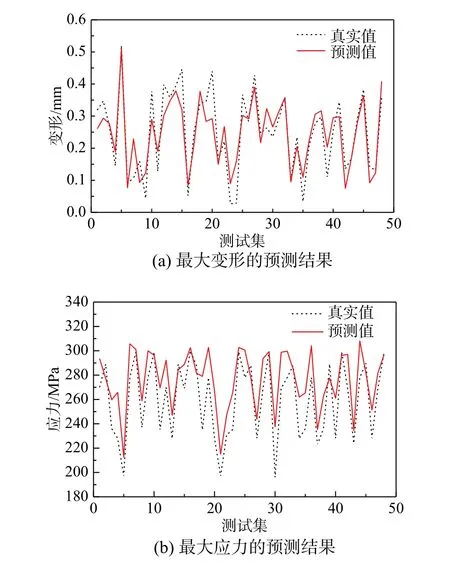
图19 神经网络预测结果Fig.19 Neural network prediction results

最后，利用MATLAB函数sim 进一步对上述网络进行仿真与计算，即：

4 遗传算法多目标优化

综上可知，通过改变零件结构，可以实现零件加工变形的控制，但也会影响零件的疲劳寿命。要使得结构件安全性能尽可能提高，应让最大变形和最大疲劳应力尽量小。因此，腹板位置的多目标优化问题可定义为：

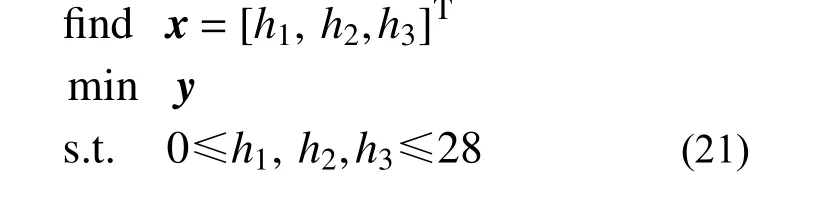
式中，h1、h2、h3为腹板底面距零件底面的距离。

在单目标优化时通常只有一个最优解，但在多目标优化时，各个目标之间通常会相互制约，可能使得一个目标性能的改善会损失其他目标的性能，不存在一个使所有目标性能都达到最优的解，所以对于多目标优化问题，其解通常是一个非劣解的集合−Pareto解集。

多目标遗传算法是用来分析和解决多目标优化问题的一种进化算法，在众多多目标优化的遗传算法中，NSGA-II算法(Elitist Non-Dominated Sorting Genetic Algorithm，带精英策略的非支配排序遗传算法)是影响最大和应用范围最广的一种多目标遗传算法[19]。

MATLAB提供gamultiobj函数来使用改进的NSGA-II算法进行多目标优化，求解式(21)中的腹板位置h1、h2、h3。

设置种群数量为200、迭代次数为200、交叉概率为0.8、变异概率为0.2，函数执行结果如表2及图20所示。

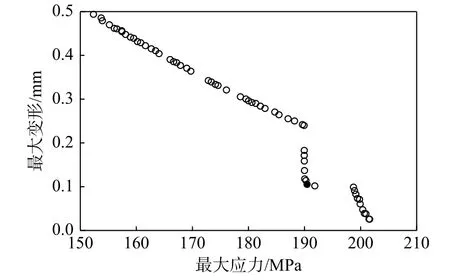
图20 Pareto前沿图Fig.20 Pareto frontier

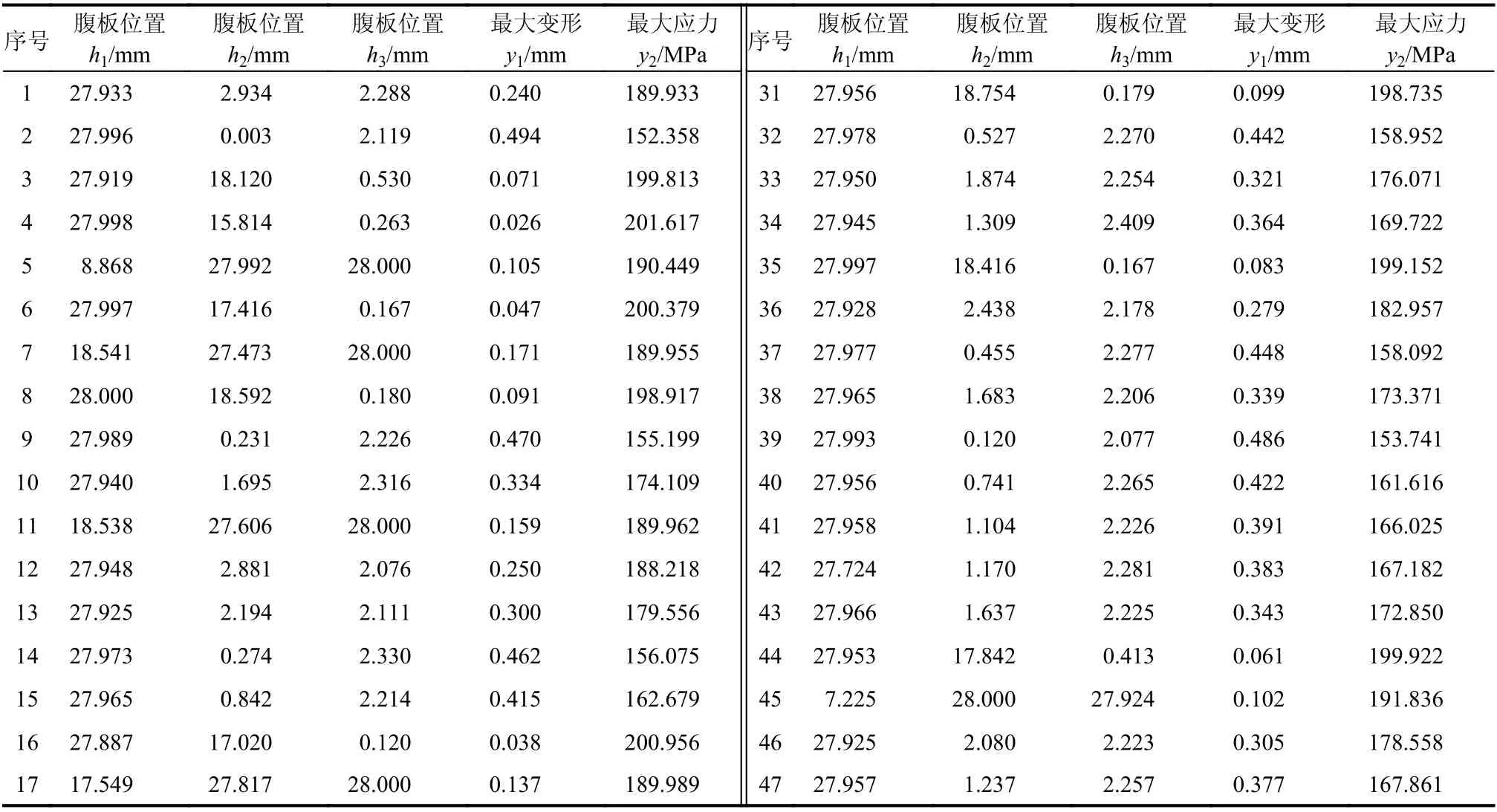
表2 Pareto最优解Table2 Pareto optimal solution

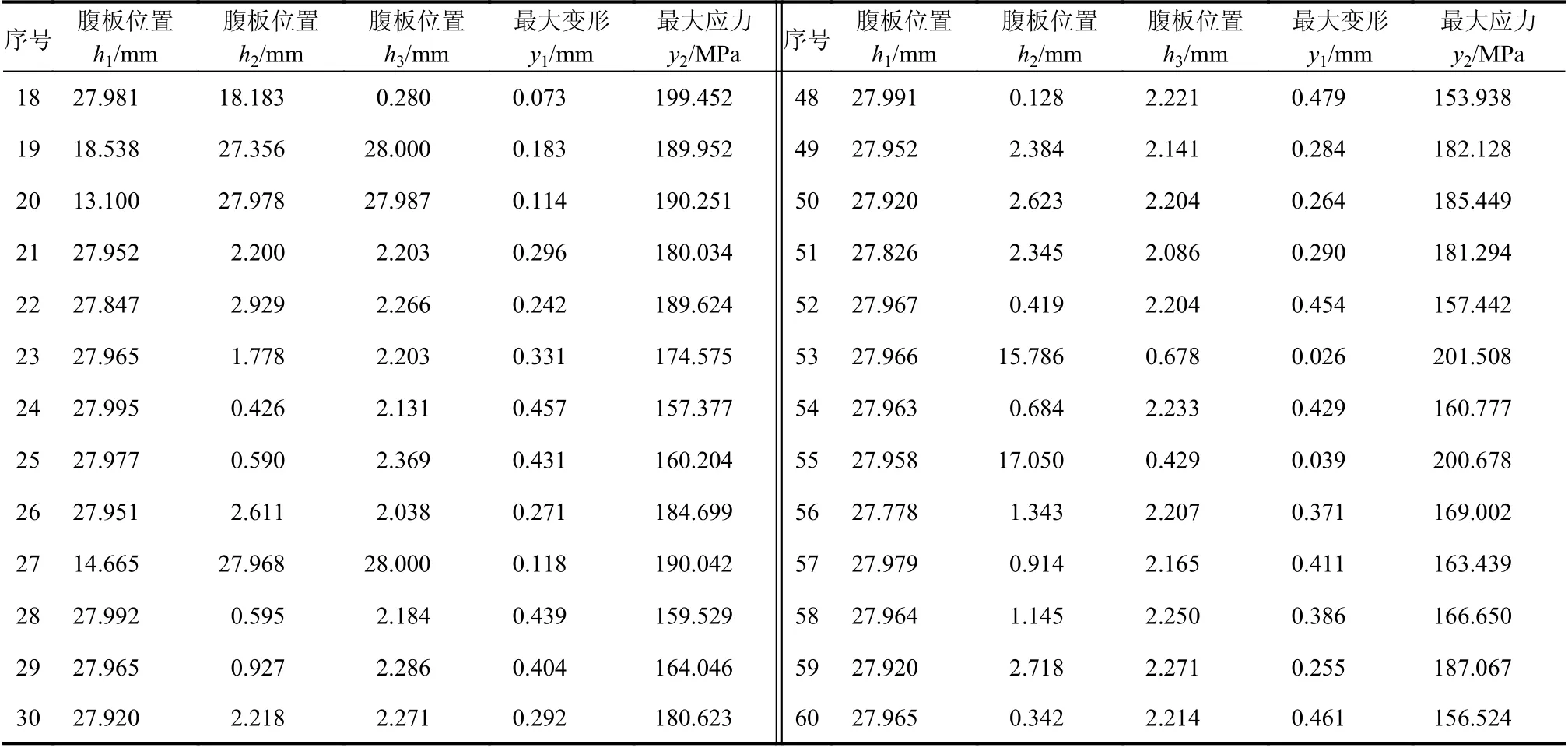
续表2

表2中的解均为最优解，为确定具体的零件结构，通过熵值法挑选序号为5的解，在图20中以黑色实心圆点表示，即h1=8.868 mm、h2=27.992 mm、h3=28.000 mm，对应的最大变形预测值为0.105 mm，最大应力预测值为190.449 MPa。而有限元方法计算得到的最大变形值为0.088 mm，最大应力值为187.7 MPa。

对最优解的结构进行静力分析时，同样采用类型为CTETRA、密度为2 mm 的单元划分网格，得到277 805个单元和92 265个节点，计算结果如图21所示。根据名义应力法，在HyperWorks软件中对优化结构进行疲劳分析，施加图14所示的随机循环载荷，疲劳分析结果如图22所示。

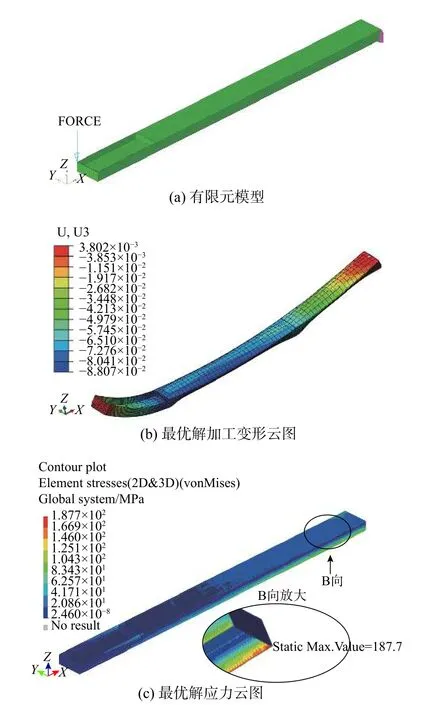
图21 最优解静力分析Fig.21 Static analysis of optimal solution

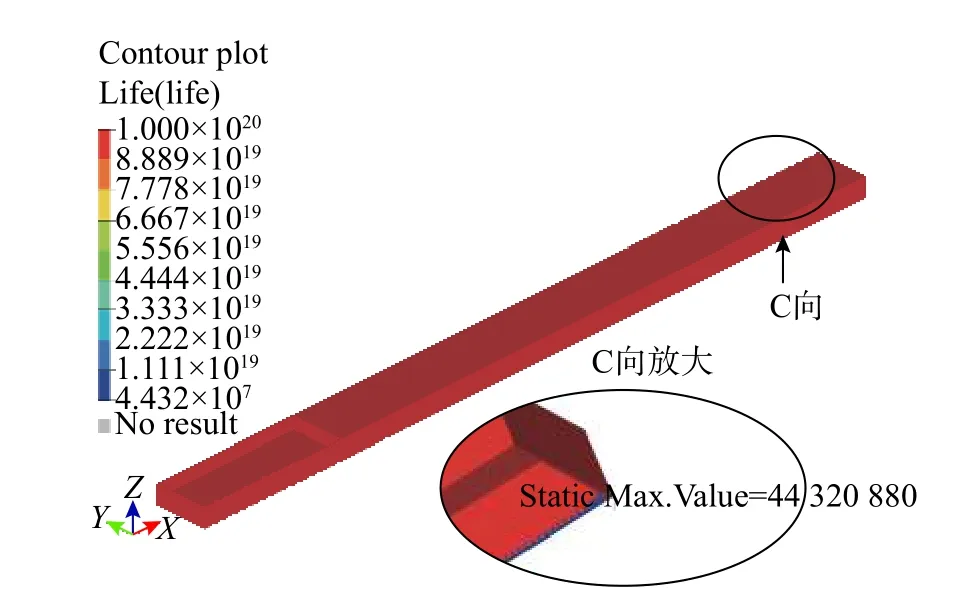
图22 最优解结构疲劳分析结果Fig.22 Structural fatigue analysis results of optimal solution

最优结构件最少能够承受图14所示的随机循环载荷共4.432×107次，危险部位出现在被约束端面附近、远离腹板的位置。与优化前的原始结构相比，加工变形减小了83.73%，疲劳寿命在随机循环载荷下提高了118.54%，如表3所示。

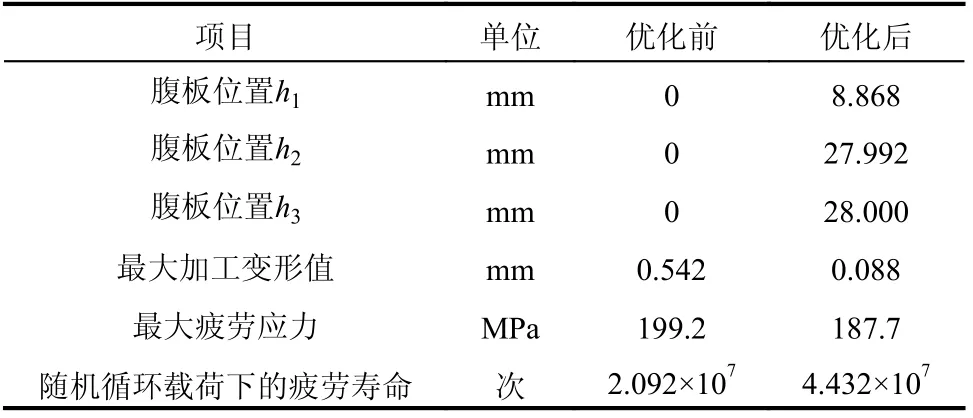
表3 结构优化前后的数据对比Table 3 Comparison before and after structural optimization

5 结论

对本文的主要研究内容可总结如下：

(1)分析残余应力释放导致的加工变形时，通过将毛坯内部的残余应力合理地等效为外载荷，计算出对应的等效力矩，利用材料力学的挠曲线方程，推导出了梁类航空整体结构件腹板位置与残余应力引起的加工变形之间的解析关系。试验结果表明，方程解析值、有限元仿真值与实验测量值在最大变形值与变形曲线上都吻合得较好。

(2)通过对名义应力法的分析，将零件最小疲劳寿命的求解简化为了对疲劳载荷下零件最大应力的求解。再利用正交表选取了236组具有代表性的样本，对其进行有限元分析求解出最大疲劳应力值及最大加工变形值。通过这236组数据，训练出了一个3-7-5-2结构的神经网络，该网络以3个腹板位置为输入、零件最大加工变形及最大疲劳应力为输出。

(3)依据腹板位置对最大加工变形和最大应力(最小疲劳寿命)的对应关系，建立了使最大加工变形与最大疲劳应力最小的多目标问题，通过NSGA-II算法解出了相应的Pareto解集和Pareto前沿。并挑选出了最合适的解，即3个腹板与零件底部的距离分别为h1=8.868 mm、h2=27.992 mm、h3=28.000 mm，此时零件的最大加工变形为wmax=0.088 mm，最小的随机疲劳载荷寿命为4.432×107次。

附表A：训练集

附表A 神经网络训练集Attached table A Training set of neural network

续表A

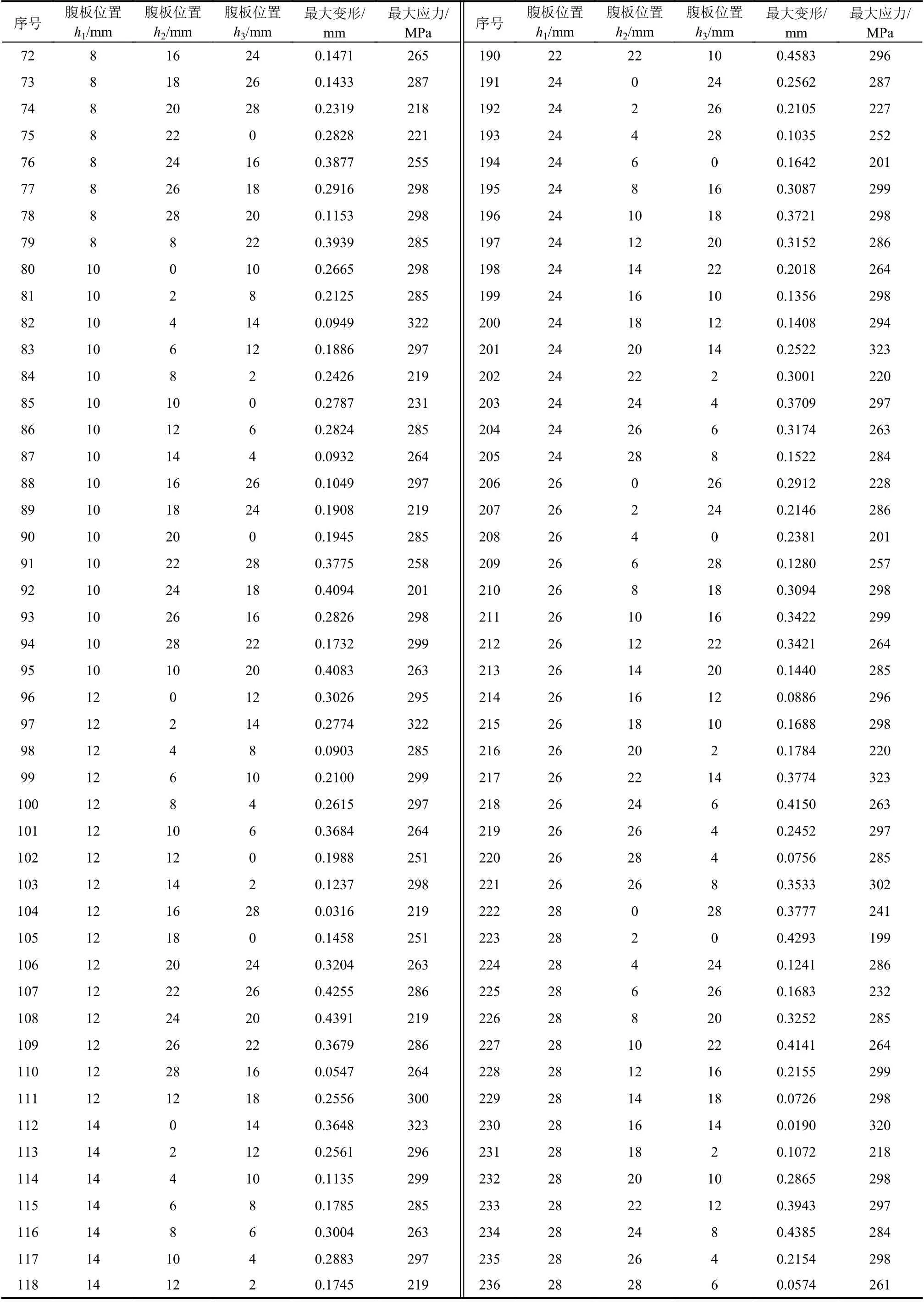
续表A

附表B：测试集

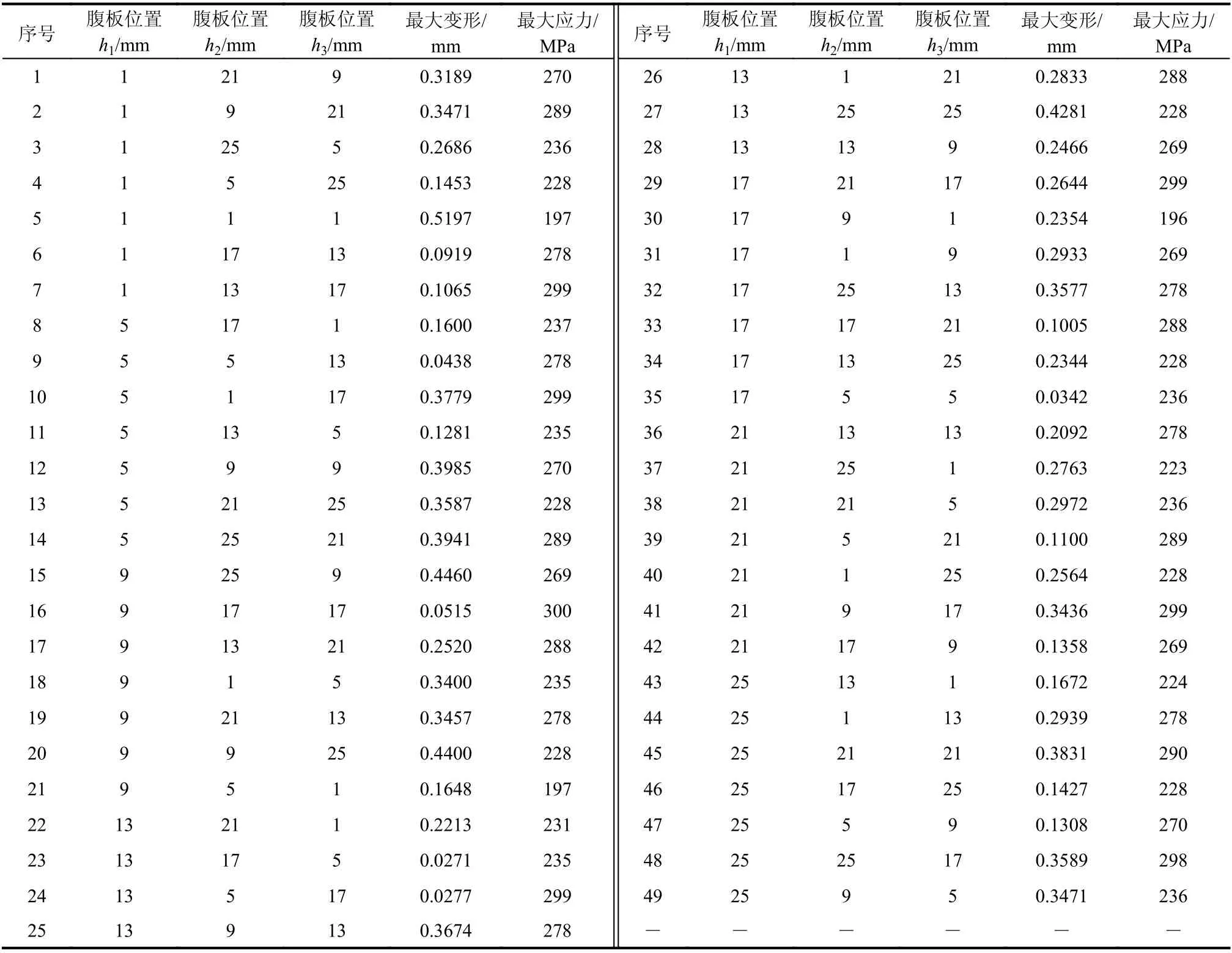
附表B 神经网络测试集Attached table B Test set of neural network