近断层地震动脉冲特性研究综述

陈笑宇，王东升，付建宇，国 巍

(1. 大连海事大学道路与桥梁工程研究所，大连 116026；2. 河北工业大学土木与交通学院，天津 300401；3. 中南大学土木工程学院，长沙 410083)

多次地震后灾害调查表明，近断层地震动对临近断层的结构物具有显著破坏性。1957 年美国Port Hueneme 发生矩震级4.7 级地震，虽然震级较小，但其造成的灾害是同等震级地震中前所未有。后续研究发现，此次地震事件中第一次记录到含有速度脉冲的地震动是造成大量结构破坏的重要原因[1]。分别发生于1966 年和1971 年的Parkfield地震和San Fernando 地震再次证实了近断层脉冲型地震动的危害[2−4]。工程师们广泛认识到地震动中的脉冲对长周期结构的破坏性并在设计中考虑其影响却始于1994 年Northridge 地震和1995 年的Kobe 地震[5]。这两次地震均发生在人口密集的城市区域，结构较普遍采用了现代抗震措施，但面对脉冲型地震动作用较多建筑仍未能经受住考验。这是由于近断层地震动携带的速度脉冲可以使结构产生较大的位移反应，使得临近断层的结构在其作用下有更高的强度和延性需求[5−11]。

对于近断层地震动脉冲特性深入研究有利于加深对临近断层结构反应的认识，从而为临近断层结构抗震设计提供理论依据，也助益于加深理解震源破裂过程。但在研究早期，受强震仪水平限制，得到的近断层脉冲型记录十分有限，难以宏观获取其统计特性。1999 年土耳其Kocaeli 地震、Duzce 地震和中国台湾集集地震中获得了大量近断层脉冲型强震记录，为近断层地震动的深入研究提供了基础数据资料。随后，2008 年汶川地震、2013 年芦山地震和2014 年鲁甸地震，我国大陆也获得了近断层强震记录。本文从强震记录处理、脉冲识别和建立地震参数统计关系等方面，对近断层地震动脉冲特性相关科研工作做简要回顾。

1 近断层地震动脉冲成因

近断层地震动在诸多因素作用下主要呈现出上盘效应、方向性效应和滑冲效应。上盘效应是地震动在上盘场地比其在距离发震断层地表迹线相同的下盘场地拥有更为剧烈的短周期振动、强震分布区域更大并且衰减更缓[12−15]。上盘效应在逆冲断层上表现尤为显著。但是低频速度脉冲主要是由方向性效应和滑冲效应引起。

方向性效应是指断层破裂朝向观测点，并以接近岩层剪切波速的速度传播，地震动能量在短时间内同时到达观测点并积累释放，在地震动记录的初始阶段形成大峰值、短持时的低频速度脉冲；而在破裂后方，地震动低频成分被削弱，能量持时长、峰值小[14,16 −17]。方向性效应从物理层面可以理解为断层破裂传播的多普勒效应，它与震源破裂机制、断层破裂方向和速度、断层面的错动方向以及破裂方向与观测点的夹角等因素相关。由方向性效应引起的速度脉冲在断层倾角较小时常出现在观测点与断层面相垂直的方向上，在断层倾角较大时，常出现在与断层走向相垂直的方向。

方向性效应的另外一层含义是在地震动空间分布上，地震动的频谱特性、持时和峰值等参数随方位角发生变化。研究发现，近断层速度脉冲在空间上可以发生在不只一个方向，并且根据观测方向不同表现出明显强度差异[18−24]。

滑冲效应与地震过程中两盘发生相对滑移或错动而产生的地面永久静位移相关，可以用弹性位错理论进行解释。在强震记录中则呈现为近似阶跃函数形式的永久位移时程。滑冲效应引起的速度脉冲常呈现为单侧脉冲，出现在平行于断层滑动的方向上。

对于走向滑移断层，在特定观测点，向前方向性引起的脉冲主要出现在垂直于断层走向的方向，滑冲效应引起的脉冲则出现在平行于断层走向的方向；而对于倾向滑移断层，向前方向性效应和滑冲效应引发的速度脉冲均大概率出现在垂直于断层面的方向，这两种效应引发的脉冲可发生耦合。

2 近断层强震记录处理

对于近断层脉冲型地震动的深入研究依赖于强震记录的准确获得。由于背景噪声、仪器噪声、地面倾斜(仪器倾斜)等因素影响，原始地震动加速度记录不可避免的存在基线偏移等问题[25−28]。这种偏移对于加速度记录影响较小，当积分为速度、位移时程时，误差却被急剧放大，对近断层地震动低频速度脉冲特性的研究造成困难。

在地震动中的低频成分获得充分关注前，高通滤波是最为广泛的强震记录处理手段[29]，美国地调局(USGS)即采用此方法开发了通用基线校正程序BAP(Basic acceleration processing)。高通滤波会滤除包含永久位移信息的低频信号，因此不适用于近断层强震记录的处理。目前，各国学者提出的适用于近断层强震记录处理的方法可总体分为两类：传统分段校正法与基于时频分析的校正方法。

2.1 传统分段校正法

Graizer 等[30]于1979 年提出强震记录中的基线偏移可以由多项式进行拟合。Iwan 等[31]于1985 年采用此方式尝试将原始强震记录分为三段进行拟合处理。该方法针对特定仪器的磁滞效应引起的基线偏移，将加速度大于50 cm/s2作为固定限值，当加速度首次大于此限值的时刻记为t1，末次大于此限值时刻记为t2，根据t1和t2将原始速度时程划分为三段，对其尾段(t2时刻到记录末端)进行线性拟合，所得斜率af即为加速度时程尾段基线偏移值，即：

式中：vc(t)为t2到记录末端的线性拟合；af为斜率；v0为截距。

中间段(t1到t2之间)加速度时程基线偏移平均值由式(2)获得：

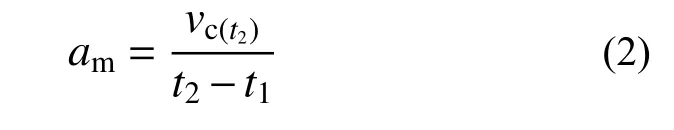
式中，vc(t2)为t2时刻线性拟合值。

尾段和中间段分别减去相应的偏移值即为校正后的加速度时程。

这个方法可以保留强震记录中的永久位移信息，但是t1和t2的选择是基于特定仪器的特定效应。基线偏移的原因多样，固定限值的选取过于主观，不适用于其它情况。

Boore[25]于2001 年对Iwan 等[31]的三段校正法进行改进。他在对集集地震记录研究时发现，此次地震中的仪器并未发现明显磁滞效应，因此在基线校正过程中放弃了将50 cm/s2作为固定限值，重新定义了t1和t2的选择标准。Boore[25]的方法中，t1和t2均被设定为可变参数，t2定义为原始速度时程tf1到tf2段拟合直线与零轴交点时刻，(tf1为强震刚刚消退时刻，tf2通常选取记录结束时刻)。t1是一个自由变化的参数，不再以某一固定限值选取，但其选取规则不唯一，这对获得稳定的强震记录的峰值位移(PGD)影响较大。

Wu 等[32]在基线校正过程中将位移时程引入，再次对关键时刻的选择标准进行优化。在他们的方法中t1的选取被明确为原始位移时程开始非零的时刻；增加参数t3(位移时程达到永久位移水平的时刻)，而后引入平坦度指标f对t2进行选择：

式中：f为平坦度指标；r为线性相关系数；b为校正后的位移时程；t3时刻到记录尾部的最小二乘回归斜率； σ为t3到记录尾部位移时程的方差。

t2可为t3到记录结束时刻之间的任意时刻，根据不同t2备选时刻对原始记录进行反复校正并计算相应f值，取f值最大的时刻为最终t2的取值。Wang 等[33]结合Boore[25]和Wu[32]的工作，引入更细致的参数确定t1和t2的选择范围，采用穷尽算法对位移时程进行非线性拟合从而获得波形上最合理的t1和t2。至此，强震记录基线分段校正实现软件自动化，降低了人为主观性，也应看到，对于关键时刻t1和t2初步范围的确定仍是基于部分物理条件设定。

国内也有学者基于Boore[25]工作做了诸多改进和在强震记录处理上的应用。王国权等[27]基于集集地震动数据对分段校正方法进行优化，于海英等[34]针对长持时的汶川地震动记录提出多段校正方法，谢俊举等[35]也在汶川地震原始记录的处理中应用分段校正法。陈勇等[36]基于最佳时段拟合思想引入均方差来确定尾段最为平稳的位移时程从而获得合适的t2；荣棉水等[37]基于陈勇等[36]的工作再次引入时移斜率比、拟合段标准差和位移时程尾段均方差三个参数对关键时刻的选择工作进行优化；张斌等[38]引入均方根偏差对关键时刻的选取进行优化。

国内外这些工作将传统分段校正方法中关键时刻的选取进行了充分优化，并应用于实践。台湾地震工程研究中心即采用传统分段校正法处理原始强震记录，建立了近断层脉冲型地震动数据库[39]。结果证明，传统分段校正法可以保留永久位移信息，处理近断层地震动原始记录是有效的，但是无法解决此类方法存在的本质问题。

分段校正法对于强震记录的处理结果高度依赖于关键时刻t1和t2的选择，时刻选点不同导致最终获得的PGD 和永久位移差异性很大；更多关注于速度、位移波形的调整，本质上去除了何种频率成分未知[26]。

在传统分段校正法中，基线偏移被简化为加速度时程上的两阶段阶跃函数，这种假设与基线偏移成因的研究结果略有矛盾。如前所述，导致基线偏移的因素复杂，对应频率成份变化多样，这种偏移应该是一个复杂的频率变化过程，而阶跃函数频率变化过于单一。随着大型、高柔结构建造越来越多，抗震分析对强震记录中更真实的频率成分(低频)还原提出了更高的要求。

2.2 基于信号时频分析的校正方法

随着信号时频分析技术的发展，诸多学者尝试通过强震记录的频域分解、去噪解决基线偏移问题。

Chen 和Loh[40]基于离散小波变换提出三相位校正方法。首先将原始加速度记录添零扩充以解决小波分解边界效应问题，而后对扩充后的数据以Meyer 小波为母波进行离散小波变换，连续分解16 层后将各层分解得到的高频项叠加重构，将重构信号积分为位移，根据三个标准确定第一相位处理后的最佳近似信号。第一相位的处理中满足了位移波形起始零值的限制并获得了稳定的PGD，但是位移时程尾部变形说明仍有低频噪声存在。将第一相位中扩充后的原始加速度信号直接积分为速度时程，对速度时程进行小波变换，同样16 层分解后将高频项逐层叠加，再将各层重构的速度时程积分为位移时程，选择一个尾部波形最平稳的信号作为最佳近似。第二相位的处理能够捕捉到位移时程平稳的尾部波形。而后在第三相位处理中，将第一、第二相位结果结合，从而获得最终校正后的记录。此方法被应用于集集地震动原始记录的处理，表现良好，但是物理基础较为薄弱。

Ansari 等[41− 42]根据小波去噪理论提出强震记录两阶段去噪方法。首先，对原始加速度记录进行N 层次小波分解，针对每一层的细节(高频)项进行降噪处理，将去噪后的所有细节项和最后一层近似(低频)项重构为新的加速度信号；而后将重构信号积分为速度时程，进行二次降噪处理，以SureShrink 程序确定去噪限，再将去噪后的细节项重构，获得降噪后的记录。该方法针对有永久位移的近断层地震动记录仍需要进一步的基线校正处理。Chanerley 等[43]也使用小波变换将原始记录分解为高频子信号和低频子信号，对高频子信号去噪，使用低频子信号估计永久位移和仪器倾斜。这些基于小波变换的强震记录处理方法与一般滤波方法假定噪声存在于某一固定频域内不同，是对全频域进行分解去噪，但是分解层数是人为主观确定的，着重于对信号进行处理，物理基础较为薄弱。

Huang 等[44]提出一种基于经验模态分解(EMD)的基线校正方法。该方法首先将原始记录低通滤波从而降低后续分解得到的本征模态分量(IMF)的阶数，而后将滤波后的信号进行EMD 分解，筛选其中几项IMF 叠加，构建基线偏移模型。这个方法虽然引入了新的信号处理技术，但是本质依旧是将原始加速度时程基线偏移假定为阶跃函数形式，并且处理结果非常依赖低通滤波限的选取，并未发挥EMD 分解的优势。笔者根据希尔伯特-黄能量密度谱分析提出了一种新的近断层强震记录基线校正方法。该方法通过对每一阶本征模态进行希尔伯特能量密度谱分析将原始信号区分为未被污染频率成份和被污染的频率成份，保留未被污染成份，针对被污染的频率成份进行处理，从而实现对于原始记录的类似“靶向治疗”的降噪处理。图1 给出了通过此方法与传统分段校正方法提取出的基线偏移的波形对比：通过新方法提取出的基线偏移包含复杂的频率变化，与传统方法相比更加符合基线偏移的物理过程。

图1 希尔伯特-黄能量密度谱方法提取出的基线偏移与传统方法提取结果的比较Fig. 1 Acceleration time history of baseline offset extracted by HSA method and that removed by traditional baseline adjustment method

综上所述，现有的近断层强震记录处理方法中，传统分段校正方法经过多年发展已被充分优化并实践应用，但是此类方法是基于加速度时程基线偏移为阶跃函数形式的假设，这与基线偏移的物理原因略有矛盾，难以在频域尽可能最大真实地还原地震动信息(尤其低频)，对于关键时刻的优化选取并不能解决此问题。基于时频分析的校正方法可以在频域内将原始地震动信号做“解剖”并还原到时域。小波变换和希尔伯特黄变换等时频分析手段都可达到此目的，但是此类方法在强震记录里中的应用和发展略显缓慢，各个方法均未被充分研究。

3 脉冲识别与参数获取

基于基线校正后的近断层强震记录，各国学者对脉冲的识别和脉冲参数的获取开展了广泛研究。从结构抗震角度，高效的识别和提取出脉冲波形，有利于“精准”描述脉冲型地震动作用下结构响应和破坏机理。在2007 年Baker[20]提出通过小波变换定量、自动化提取脉冲之前，近断层地震动的相关研究主要是通过构建各种数学模型来表征地脉冲特性。在Baker[20]小波方法提出后，又有一些采用信号处理手段的脉冲研究方法面世。

3.1 数学模型表征脉冲

Alavi 和Krawinkler[45− 46]界定了单侧、双侧和多脉冲三种脉冲形式，采用方形波表征脉冲加速度时程。Makris 和Black[8,47− 48]同样针对这三种脉冲形式以简谐波构建脉冲模型。Menun 和Fu[49−50]尝试采用较为复杂的复合函数表征速度脉冲，并于2004 年根据Haskell 震源模型对近断层脉冲的数学模型进行改进。李新乐和朱晞[51]在Menun 和Fu[49− 50]的工作基础上提出改进的等效速度脉冲模型，并讨论了脉冲模型参数的确定方式；田玉基等[52]采用连续函数建立等效速度脉冲模型。

在众多脉冲表述的数学模型中，Mavroeidis和Papageorgiou[53]于2003 年构建的模型应用最广。该模型对Gabor 小波进行修改提出了M&P 小波：

式中：t0为包络曲线峰值时刻；其余参数同上。脉冲周期取为中心频率fp的倒数。

此模型可以模拟脉冲的速度、加速度、位移时程和相应反应谱，与其它数学模型相比变化灵活，更接近于实际脉冲波形，并且在将其作为输入研究单自由度体系地震反应时能够获得封闭解。李帅等[54]采用Butterworth 滤波器将实测近断层强震记录分解为高频无脉冲速度时程和低频脉冲速度时程，而后以M&P 速度脉冲模型对低频速度时程进行拟合。Dickinson 和Gavin[55]基于Gabor小波也建立了速度脉冲模型。这些数学模型统一存在的问题是脉冲周期、幅值、位置、相位等重要参数需要提前获取，而对于多脉冲情况，脉冲个数更需要人为确定。针对M&P 模型，Mimoglou等[56]优化了各参数自动化确定过程，他们建立了Sv×Sd谱，由此卷积谱峰值对应的周期作为脉冲周期，再通过建构小波的累积绝对位移(CAD)与反应谱峰值的关系获得其它参数，此优化程序后续应用较少，原因尚不清楚。

另外，数学模型表述只是对于近断层地震动中脉冲波形的拟合重现，无法对一条强震记录是否为近断层脉冲型进行判别。有学者基于这些数学模型针对脉冲型记录的判别开展了部分工作。Vassiliki 等[57]采用M&P 小波作为母波，将M&P小波与强震记录的互相关系数作为脉冲判定指数，当此系数大于0.65 时地震动记录可被判定为脉冲型，当系数小于0.55 时即为非脉冲型记录。翟长海等[58]采用Dickinson 和Gavin[55]提出的脉冲模型构造速度脉冲，而后由其是否占总能量30%来对脉冲型地震动进行判定，其中脉冲周期采用峰点法确定。常志旺等[58− 59]在2016 年对此方法进一步修正。这些方法虽然能够粗略实现脉冲型地震动的判定，但是脉冲参数需要人为确定的困难仍无法解决。

3.2 基于信号处理的脉冲识别方法

随着信号处理工具的发展，对于脉冲型地震动定量的自动化判别成为可能。Baker[20]基于小波变换提出脉冲型地震动定量判定方法。该方法以Db 小波为母波，对地震动记录速度时程进行连续小波变换，提取出系数值最大的小波，而后通过三个标准判定提取出的信号是否为早到脉冲——即向前方向性效应引起的脉冲，需同时满足的三个判定标准为：

1)以幅值比和能量比为参数通过回归分析获得脉冲指数(PI)，当PI>0.85 时，提取信号即可被判定为脉冲，当PI<0.15 时即为非脉冲；

2)脉冲能量积累达到10%的时刻早于原始地震动总能量累积达到20%时刻；

3)原始地震动速度峰值大于30 cm/s。

判定为近断层脉冲型地震动后，提取出的携带最大小波系数的小波即为地震动中的等效速度脉冲波形，脉冲周期定义为提取出的小波最大傅里叶幅值对应的周期。这是目前近断层脉冲型地震动研究工作采用最多的方法。该方法中，母波的选取虽然对脉冲型地震动判定影响较小，对脉冲周期求解影响却十分显著[60−61]。小波系数表征的是相关小波的能量，提取最大系数的小波本质即为找到能量最大的小波。因此，对于多脉冲情况，此方法只能提取出一个能量最大的脉冲。

Lu 和Panagioto[62]根据Baker[20]的小波方法，以M&P 小波为母波，针对多脉冲记录提出了迭代提取的方法。这个方法中，脉冲个数与提取次数并不完全相关，且每次提取出的脉冲在时域上相重叠，无法将各个脉冲发生时刻准确定位，如图2所示。

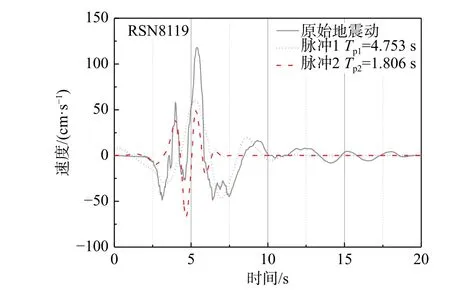
图2 迭代提取方法两次提取获得的速度脉冲(2010 年新西兰，Christchurch 地震，PRPC 台站)Fig. 2 Pulses extracted by iterative procedure for velocity time history recorded in Christchurch earthquake at PRPC station

针对向前方向性脉冲，Xu 等[63]提出了多尺度分析法，仍可以理解为小波变换的扩展。Chang等[64− 65]在近期研究工作中发现，对于向前方向性效应引起的脉冲，波形相似的速度脉冲有可能是由完全不同的频率成分构成(既可以由加速度脉冲积分而成，也可由加速度时程单侧高频振荡积分而成)，同时携带加速度脉冲和速度脉冲的地震动对短、中周期(1.5 s～2.5 s)结构有显著影响，而非加速度脉冲型速度脉冲记录对长周期(大于4 s)结构影响显著。因此他们通过小波包变换提取出速度脉冲，而后根据能量占比将速度脉冲型地震动继续深入判定，划分为加速度脉冲型和非加速度脉冲型。这是近断层地震动中加速度脉冲首次受到特别关注，为近断层地震动脉冲特性的研究提供了新的视角。

翟长海等[66]提出了脉冲型地震动的能量判定方法。该方法可以对所有携带速度脉冲的地震动记录进行判定，并未明确针对的是何种效应引起的速度脉冲，应该注意盆地效应、软土场地及液化等也会产生速度脉冲。他们将速度时程离散为多个半圈(half-cycles)，根据重要半圈能量占地震动总能量的比值，划分为五种情况对脉冲型地震动进行判定，但无法同时获取如脉冲周期等重要的参数，并且脉冲个数要人为确定。Zhao 等[67]也提出了一个基于三角函数和速度穿零点判定脉冲型地震动的方法(ZVPM 方法)，也无法获得等效脉冲。

笔者以希尔伯特-黄变换(HHT)为基础，提出了近断层地震动速度脉冲判定、波形提取和重要参数确定的自动化方法[68−69]。该方法将频率与能量相结合，认为速度脉冲是由记录中能量贡献较大的低频成份组成。这个方法与前述方法关注于地震动整体波形不同，而是着重把握脉冲的低频特性。因此通过HHT 方法提取的脉冲幅值不完全等同于原始记录的峰值。首先，将记录的速度时程通过聚合经验模态分解(EEMD)为表征不同频率成分的IMF，以PGV/PGA 比值作为频率判定标准(PGV/PGA 大于0.12 即为低频)、以能量贡献率(ΔEc(n))表征各IMF 分量对原始地震动总能量的贡献，如果存在某一阶IMF 能量贡献大于0.32，且其PGV/PGA 比值大于0.12，该记录即可被判定为脉冲型地震动；所有能量贡献率大于0.1 的低频分量叠加即为提取出的粗糙速度脉冲信号；而后通过雨流计数法去除时域内“脉冲不相关”信息，最终将单个或多个脉冲准确定位在时域上，它们可以不连续。该方法通过一次提取即可获得脉冲个数、脉冲周期和脉冲幅值。目前，主要应用于处理向前方向性效应引起的脉冲型地震动。若对近断层速度脉冲成因感兴趣，可结合震源信息对提取后的脉冲进行后续研究。

近二十年来，针对近断层地震动脉冲识别与提取学者们提出了诸多方法，使近断层脉冲型地震动的批量获取以及后续的深入研究成为可能。目前，绝大多数方法的开发都是基于向前方向性效应引起的速度脉冲，相比之下，针对滑冲效应引起的脉冲研究较为不足。一些方法可以对脉冲型地震动进行判定和提取，但是无法对不同效应引起的脉冲进行深入识别。应该指出，不同的脉冲成因导致不同的脉冲特性，如有学者指出，与向前方向性相比，滑冲效应引发的脉冲潜在破坏作用更大[70]。在后续研究中，除向前方向性效应引起的脉冲外，滑冲效应引发的脉冲特性值得同等关注，也包括二者的耦合出现。

另外，若干学者在研究中发现，除水平方向外，近断层地震动竖向分量中也会存在显著速度脉冲，且其影响不可忽视[71−75]，其在近断层速度脉冲提取工作中仍缺乏独立、系统的讨论。

4 脉冲参数统计特性

通过前述方法提取出近断层地震动脉冲波形后，各脉冲参数与地震参数的统计关系可以获得。

4.1 脉冲个数与地震参数关系

Somerville 等[16]早在1997 年即提出近断层地震动中速度脉冲个数与一个断层内的破裂面相关；Bray 和Rodriguez-Marek[76]也曾指出一条地震动记录中速度脉冲数与断层滑移分布相关。这充分说明近断层地震动速度脉冲与断层及破裂过程关系密切，可作为地震震源反演的信息使用，而不仅仅是出于结构抗震研究需求[77−79]。

目前对速度脉冲个数确定的研究工作尚不充分。Bray 和Rodriguez-Marek[76]通过将脉冲幅值折减50%作为独立的脉冲个数，他们自己也承认这很主观。翟长海等[66]提出的脉冲型地震动的能量判定方法给出了多脉冲的判别，而细节性信息不足。最近笔者基于前述HHT 方法对86 条近断层强震记录中的脉冲个数进行统计分析，认为速度脉冲个数与断层类型、断层距、场地条件相关[69]。与走滑断层相比，多脉冲更易发生在逆断层和逆斜断层(reverse-oblique fault)；针对场地条件，脉冲个数随着场地条件Vs30(地下30 m 平均剪切波速)的增加而减小。综合考虑断层距与场地条件，多脉冲地震动更易发生在相对集中的区域(图3)。土层对于地震动中长周期成份有放大作用，这使得在较软场地可以识别到更多的脉冲。

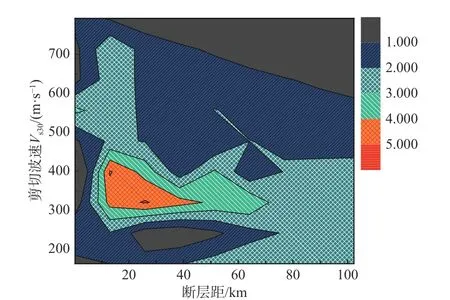
图3 速度脉冲个数与断层距、30 cm剪切波速(Vs30)关系Fig. 3 Contour map of rupture distances, shear wave velocity and number of inherent pulses

4.2 脉冲周期与地震参数关系

在众多研究中比较统一的认识是，速度脉冲周期与矩震级相关，也受场地条件影响。

近断层地震动速度脉冲周期与矩震级的关系已在众多研究工作中得到证实，各个统计回归公式列于表1，示于图4。从总体趋势来看，脉冲周期随震级的增加而增加，各个统计关系式间的差异来源于脉冲周期的定义和采用数据构成不同。在众统计模型中，Mavroeidis 和Papageorgiou 采用42 条记录，而笔者工作基于PEER 数据库中86 条近断层脉冲型记录，注意到笔者提出的统计模型和谢俊举等[80]考虑汶川强震记录后提出的模型最为相近。通过的统计分析发现脉冲周期也与断层类型有关，这在以往研究中未曾揭示[69]。Mavroeidis 和Papageogiou 的模型在小震级时吻合走滑断层统计规律，而在大震级时倾向于逆斜断层(reverse-oblique fault)。谢俊举等[80]提出的模型由于考虑了以逆冲断层为主要构造形式的汶川地震，统计分析结果则更为靠近逆斜断层的统计公式。三者之间认识是一致的。

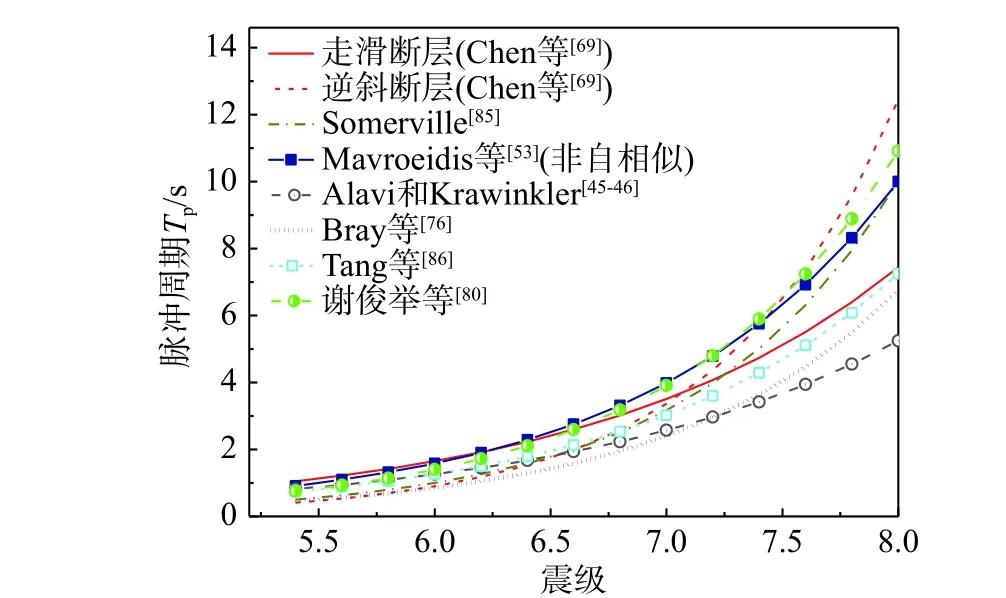
图4 速度脉冲周期与震级关系统计回归Fig. 4 Relationship between pulse period and moment magnitude

表1 速度脉冲周期与震级关系Table 1 Regression analysis of relationship of pulse periods and moment magnitudes

一些学者认为近断层地震动脉冲周期与板内地震和板间地震也具有很强相关性[81−83]。Cork 等[81]根据板内地震、板间地震将地震动记录分类进行回归统计发现：在同等震级下，板间地震记录的脉冲周期远大于板内地震记录的脉冲周期，这是由于板间地震的应力降一般来讲要低于板内地震。笔者也提出，近断层地震动脉冲周期与震级的关系与断层类型相关：对于走滑断层，脉冲周期随震级增长较缓，而对于逆斜断层，脉冲周期随震级增长较为快速。针对多脉冲情况，在同一条近断层地震记录中，所有速度脉冲的周期处于相近水平，可以由能量最大的脉冲(主脉冲)周期线性表达[69]。台湾学者仅以台湾近断层强震记录回归了脉冲周期与矩震级的关系，认为还是存在地区差异的[39]。

Rodriguez-Marek 和Bray[84]于2006 年针对场地反应对近断层地震动方向性效应脉冲参数的影响进行了较为全面的分析。土层场地的脉冲周期要普遍大于岩石场地记录到的脉冲周期，并且随着输入地震动脉冲周期的增加，土层场地与岩石场地记录到的脉冲周期的比值趋向一致。很多学者根据可以获得的数据资料对不同场地记录到的脉冲周期进行统计回归，结果如图5 所示。矩震级小于7.2 时，土层场地记录到的脉冲周期明显大于岩石场地的脉冲周期，随着震级的继续增加，两类场地的脉冲周期趋向于同一水平。由于脉冲周期的定义不同、采用的数据量不同，各个回归模型有些许差异，但是统计回归的总体趋势是相近的，能够和理论认知相互佐证。

图5 速度脉冲周期与场地条件关系统计回归Fig. 5 Relationship between pulse periods and site conditions

4.3 脉冲幅值与地震参数关系

与近断层地震动速度脉冲周期相比，脉冲幅值的影响因素较多，其与断层距和场地条件均相关，但是脉冲幅值与震级的关系目前在研究中并未达成共识。

在同等断层距下，土层场地记录到的速度脉冲幅值要大于岩石场地。这是由于近断层地震动作用下，土体反应对长周期信号有放大作用。无论何种场地条件，记录到的脉冲幅值随断层距的增加均有明显衰减。关于近断层地震动脉冲幅值的各个统计回归公式列于表2。多数学者在对脉冲幅值进行统计回归分析时将震级作为影响因素纳入回归公式。部分学者认为脉冲幅值与震级并不具有明显相关性，因此在统计分析中只考虑断层距影响[81,83]。笔者研究发现，震级对脉冲幅值的影响根据断层类型的不同有所差异。对于逆斜断层，震级项系数仅为0.08，对脉冲幅值影响较小；对于走滑断层，震级项系数达到0.2，对速度脉冲幅值影响较为明显。

表2 速度脉冲幅值统计回归关系式Table 2 Regression analysis of relationship of pulse PGV and earthquake parameters

针对多脉冲情况，在研究工作中界定了能量主脉冲，发现主能量脉冲多数为发生在时域的第一个脉冲，在一条近断层强震记录中，随着脉冲个数的增加，脉冲幅值呈现线性衰减，每一个脉冲的幅值均可以用主能量脉冲幅值以线性函数表征。

获取准确的脉冲参数统计关系有利于近断层区域的地震危险性分析及特定场地下的结构抗震设计等工作开展。目前来看，统计关系仍依赖于数据样本的选取和处理，因此，不同学者的分析结果会存在些许差异。另外，统计工作结果的阐释仍需深入的理论分析佐证，这依赖于地震工程和地震学界对相关问题的深入讨论和研究。目前针对断层类型与脉冲参数关系的讨论依然较少，这二者是近断层脉冲特性不可忽视的影响因素，很值得更多关注。此外，统计分析工作目前主要关注于水平向地震动中的脉冲，对于近断层竖向地震动中的脉冲特性研究尚未见到。

5 脉冲特性对结构反应的影响

近断层地震动会很大程度增加临近断层结构的强度和延性需求，造成较大的地震破坏[87−89]。脉冲周期、幅值以及脉冲个数等参数对结构反应的影响较为显著[54,90 −91]。速度脉冲对结构反应的放大作用体现在反应谱上，为以脉冲周期(Tp)为中心的单峰曲线，且在0.9Tp处放大效应最强，具有显著影响的周期范围为0.5Tp～2Tp[22]。同时，较大的PGV/PGA 值使得加速度反应谱具有较宽的加速度敏感段，这增加了结构基底剪力、层间变形和延性需求[87]。对于隔震结构，脉冲特性与其动力响应的相关程度尤为密切[92−98]。长周期、大幅值速度脉冲使隔震支座位移显著增加，造成耗能构件的破坏[92−95,97]，对于高阻尼橡胶支座还要考虑其速度相关性在脉冲作用下的表现[98]。有研究表明，基础隔震体系动力响应的最大值与脉冲周期、PGV/PGA 正相关，其减震率与此二参数负相关，脉冲幅值对基础隔震体系的减震效果影响则相对集中，可作为隔震体系的重要评价指标[96]。

近年兴起的自复位结构，因其兼具高耗能、小残余位移的特性而获得大家广泛关注[99−105]。在近断层脉冲型地震动作用下，自复位结构表现为泛旗帜型滞回模型，其弹塑性位移谱随T/Tp值增大呈现出先增大后减小的趋势，谱峰值对应T/Tp值为1[101,105]。脉冲特性对楼层反应谱也同样具有放大效应[106−107]。当结构周期与脉冲周期相近时，楼层位移反应谱值和加速度反应谱值均明显增大。

针对脉冲个数对结构反应的影响，有研究指出，当脉冲个数为奇数时脉冲对结构反应的影响更为显著[54]。受限于实际地震动中的多脉冲及其相关参数研究的局限，脉冲个数对结构动力响应的影响仍有待深入研究。

6 结论

随着人类社会的发展，工程建设已无法完全避开临近断层区域。从20世纪至今发生的多次大地震表明近断层脉冲型地震动对结构有显著破坏作用，与震源过程也密切相关。深入研究近断层地震动脉冲特性对结构抗震设计、地震危险性分析和震源破裂过程联合反演等相关研究具有重要意义。本文对近断层原始强震记录处理、脉冲识别和提取以及脉冲参数的统计分析等研究工作进行了简要评述。

(1)对于近断层原始强震记录处理，传统分段基线校正法的阶跃函数形式假设过于简单，基于时频分析的校正方法在此方面逐步表现出优势，宜被充分重视。

(2)近断层地震动脉冲识别与参数获取大多基于向前方向性效应，针对滑冲效应及二者耦合引起的脉冲研究不足。近断层竖向地震动中脉冲的形成机理也需独立研究。

(3)脉冲参数与地震参数关系仍需要地震学等相关理论支持及实证分析，如断层类型等因素对脉冲参数影响，也包括震源破裂过程与脉冲特性参数的关系等。

(4)真实脉冲参数的准确获得有利于加深对临近断层各类结构动力响应的理解，从而对其施行更加高效的抗震或减震设计。