基于六旋翼无人机搭载风速仪的边界层风剖面实测研究
李正农,冯 豪,蒲 鸥,沈义俊
(1.湖南大学建筑安全与节能教育部重点实验室,湖南,长沙410082;2.海南大学土木建筑工程学院,海南,海口570228)
大气边界层是大气层靠近地面约1 km~2 km的薄层,在该区域气流受地面粗糙度的影响严重[1]。目前,在边界层海拔100 m 以下的低空区域,通常使用测风塔进行定点的风速风向测量[2−3]。测风塔可以提供长时间的稳定测量,但其安装难度大、成本高,且设塔位置受限,对于多位置测量(如建筑物周围和风力发电机现场)有一定难度[4]。另外,在边界层海拔1 km~2 km 的高度内可以利用风廓线雷达进行远程风测量[5],但其价格昂贵,且空间分辨率有限[6]。
随着无人机技术的发展,由于无人机所具备的空间灵活度高、操作简单、成本低等关键优势已经越来越明显,研究者们逐渐将无人机投入到测风研究中,或能替代测风塔及风廓线雷达等方式成为新的精确广泛的测风方法。在1992年,澳大利亚气象局的Holland 等[7]首次提出了利用搭载皮托管及相关仪器的小型无人机测量风场的方法;2008年,Reuder 等[8]利用小型固定翼无人气象观测站(SUMO)对边界层气象要素及风速风向进行了实测,然而,使用固定翼无人机进行风场测量时无人机处于水平飞行状况,无法测量某一地点的垂直风剖面[9]。相较之下,多旋翼无人机凭借可垂直起降和定点悬停的优势,成为更理想的测量垂直风剖面与获取固定位置风场参数的平台。2015年,Marino等[10]提出了一种新的传感方法,可以确定迎风面的流速大小和方向;2017年,Palomaki 等[11]使用四旋翼无人机的姿态数据间接估算了10 m 高度处的风速和风向并与固定测风塔进行对比,测量误差分别为风速误差小于0.5 m/s,风向误差小于30°;2018年,Prudden 等[12]在四旋翼无人机上的多个方向安装了多孔压力探针(MHPP),通过在一定高度范围内的实测证实其风速测量的可行性,但是其探测范围仅局限于90°的迎风面锥形区。
应用六旋翼无人机搭载风速仪进行边界层风场的风剖面及脉动风特性的测量与研究开展较少,本文利用搭载风速仪的六旋翼无人机进行测量,并以北京延庆某测风塔为参考,通过对比无人机测量结果与测风塔测量结果,来探究无人机测量风场的可行性;通过对数据的分析及拟合,实现无人机对风剖面及脉动风特性的拟合测算;并将实测及分析结果与各国规范[13−17]进行对比,其结论可为无人机测量风场的研究提供参考。
1 试验概况
1.1 实测场地概况
本试验在北京市延庆区中科院电工所进行,如图1所示(实测场地为星标标记处),实测场地西北侧与东南侧为高山,西南侧较为开阔。图2给出了实测场地周围的地貌,可见西面远处低矮建筑较多,而场地周围近处基本为空旷农田,按照《建筑结构荷载规范》(GB 50009−2012)[13]有关地面粗糙度的分类标准,该场地为典型的B类场地(地面粗糙度值为0.15)。另外,该实测场地在冬季盛行西风及西北风,风场较稳定,4级、5级风较为常见,试验条件比较理想。

图1 北京延庆实测地点地形地貌图Fig.1 Topographic map of Yanqing sitein Beijing

图2 北京延庆实测地点卫星图Fig.2 Satellite map of Yanqing site in Beijing
在图2中的实测场地星标标记处架立了一个如图3所示的40 m 高的测风塔,分别在10 m、20 m、30 m、40 m 高度处各安装有一个风速仪。风速仪正北向安装,此时风向角定义为0°,正东向来风风向角为90°,按顺时针方向依此类推。测风塔的实测结果可以校准与优化无人机所测的风速风向值,以提高实验结果的精确性。

图3 北京延庆实测测风塔Fig.3 Wind tower in Yanqing,Beijing
1.2 试验装置
测风塔上安装的风速仪为GILL 三维超声风速仪,采样频率为1 Hz,并在风洞中进行了标定,误差小于±0.5%。如图4(a)所示,无人机型号为大疆M600PRO,具有稳定性强、悬停精度高的特点,其飞行垂直误差±0.5 m,水平误差±0.5 m,单次航行约30 min。无人机上搭载的风速仪为赛能超声风速仪,通过改装可以由无人机直接供电。该风速仪的采样频率为1 Hz,与测风塔风速仪相同,并且与气象部门所使用风速仪的采样频率一致。将小型电台与风速仪连接,实现无线远程实时传输(见图4(b))。

图4 实测所用系统Fig.4 System used in the measurement
由于旋翼转动引起的扰流会对安置在中央架的风速仪测风的准确性产生影响,需要对风速仪的安装高度进行探究,经过李正农等[18]的研究,将风速仪安装在机身中央架上方0.53倍旋翼直径高度处,可以减小桨叶转动产生的气流对风速仪测量数据的影响。另外,以上六旋翼的型号与参数选择及风速仪安装的具体参数皆只适用此实验,其普适性暂未深入探究。
2 风特性参数分析方法
2.1 平均风速和风向角
风速风向时程由风速仪直接测得,对风速时程按式(1)分解,得到x、y方向的分量ux(t)、uy(t)(如图5所示):

图5 风速、风向示意图Fig.5 Schematic diagram of wind speed and direction

式中:ux(t)为N方向分解风速时程;uy(t)为E方向分解风速时程;u(t)为风速时程;θ (t)为风向角时程。
则在测量时距内平均风速U与平均风向角φ可根据式(2)~式(5)计算:


2.2 平均风剖面
在大气边界层中,风速随高度发生变化,该规律可形成平均风速剖面。目前多使用指数率与对数率模型[19−20]来拟合风剖面,本文将采用中国规范使用的指数率模型式(7)对风剖面进行拟合:

式中:z为离地高度;Uz为z高度处的风速;α 为地面粗糙度的参数。
2.3 湍流度
湍流度是对气流速度脉动程度的一种度量指标,定义为平均时距内脉动风速均方根与平均风速的比值,即:

式中:i指代顺风向u及横风向v;Ii为i风向湍流度;σi为i风向脉动风速均方根;U为平均时距内的平均风速。
2.4 阵风因子
阵风因子是考虑到瞬时风较平均风大而乘的系数,一般定义为阵风持续时间内平均风速的最大值与平均时距内的平均风速的比值,如式(9)所示:

式中:Gu为顺风向阵风因子;Gv为横风向阵风因子;tg为阵风持续时间,本文取tg=3 s;u(tg)为tg内的顺风向平均风速;v(tg)为tg内的横风向平均风速。
2.5 湍流积分尺度
湍流积分尺度是对脉动风旋涡尺寸的度量,反映了湍流空间中两点脉动风速的相关性。本文根据Taylor 假设自相关函数积分法来计算,即:
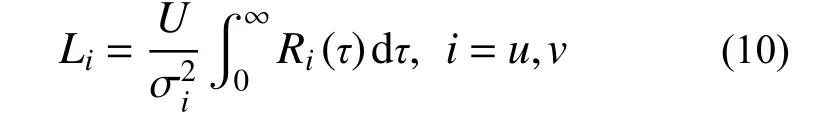
式中:Li为i风向湍流积分尺度;Ri(τ)为i风向脉动风速自相关函数。
2.6 脉动风速功率谱密度函数
脉动风速功率谱描述了脉动风速能量随频率变化的分布情况,反映了脉动风中不同频率成分对湍流脉动总动能的贡献。基于Kolmogorov 理论的统一表达式为:

目前的研究中常使用的顺风向脉动风速功率谱经验谱有Davenport 谱、Kaimal 谱和Karman 谱等[21]。本文也将以这些模型作为标准进行对比,并根据拟合结果给出了Karman 谱表达式:

3 实测结果分析
3.1 平均风特性
3.1.1平均风速和风向角
在实测中,由于无人机的自身抖动、倾角等机身姿态的影响,其搭载风速仪所测数据与测风塔风速仪所测数据存在一定误差。因此,将无人机定位在测风塔正南方向水平距离5 m 的定点处,在该定点竖向的4个垂直高度(10 m、20 m、30 m、40 m)上进行了风场测量,每次测量时长为10 min,并进行多次实测与对比分析。并结合相关论文的研究,李正农等[18]通过推算倾角进行了风洞试验,试验表明无人机所测风速随机身的倾斜角度增大而增大,且当控制风速为8 m/s时,无人机测得风速相比水平时测得风速增大约3%;当控制风速为10 m/s时,无人机测得风速相比水平时测得风速增大约6%。根据该结论,由于实测中风速不恒定,风场状态与风洞中有区别,且无人机处于悬停状态,机身抖动同样会造成一定影响,因此结合李正农等的研究与实测对比分析对无人机搭载风速仪所测量得到的风速时程进行了如式(13)的修正,同时具体修正系数λ,见表1。

表1 无人机机身修正系数表Table 1 MUA fuselage correction coefficient

式中:u(t)为机身姿态修正后的风速时程;uw(t)为无人机实测风速时程。
表2给出了一组40 m 高度处的风速数据,记录了无人机机身姿态修正前后的相关风速数据与测风塔数据的对比。与测风塔原始数据进行对比可以发现,无人机机身姿态修正后,平均风速误差由原始数据误差的3.04%减小到0.76%,平均风速得到了较好的修正。另外,对比x、y方向的分解风速,所得结果误差也有所减小,并控制在3%以内;两者风向角基本吻合,误差较小。
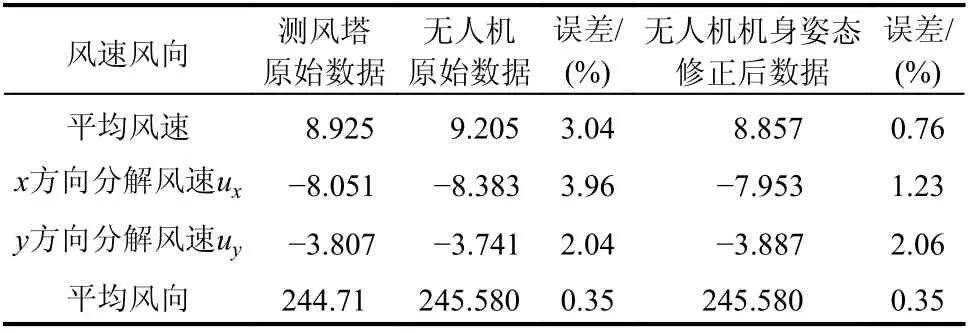
表2 机身姿态修正后无人机与测风塔风速风向对比Table 2 Comparison of wind speed and direction of drone and wind tower after airframe attitude correction
表3中记录了10 m~40 m 各高度处经过机身姿态修正后的无人机所测的风速及风向角均值以及测风塔所测的对应值。由表3可见,经过修正后,基于无人机所测的风速与测风塔对应值的误差均控制在±3%以内,风向角两者误差在±0.5%内。由此认为,机身姿态修正能对基于无人机所测的风速起到较好的校准作用,使无人机的测量值更加精确,贴近测风塔值。
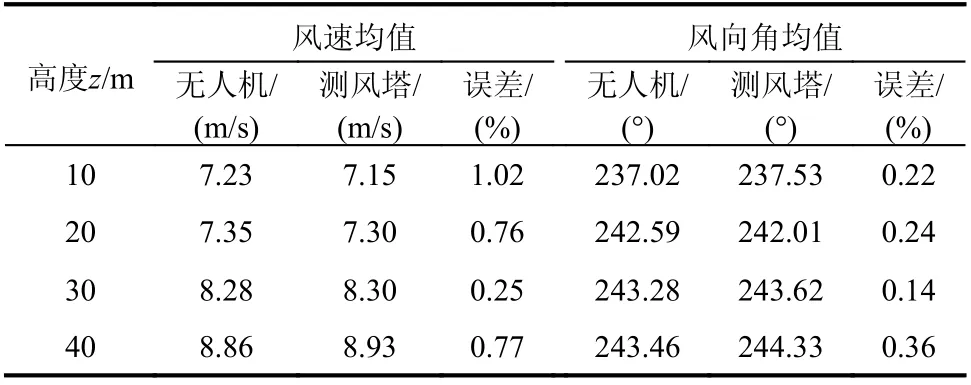
表3 不同高度处无人机与测风塔风速风向对比Table 3 Comparison of wind speed and direction between UAV and wind tower at different heights
3.1.2平均风剖面及粗糙度
在实测中由于仅有一台无人机,单台无人机无法同时在用一时距内完成10 m~100 m 各个高度风速的测量,而在不同时刻由于风速及湍流度的不同,某一固定高度的风速风向会有所区别,如果利用不同时刻无人机所测得的风速来拟合风剖面将会产生较大误差,因此需将所有高度处的风速归一化。每次测量为10 m~100 m 中的10个高度(以10 m 为增量),这里将每次在10 m 高度测量的时刻称为t1时刻,并将其余高度及时刻的风速统一以t1时刻为基准进行归一化处理,从而近似得到在t1时刻10 m~100 m 各个高度处的风速。风速归一化需要将测风塔40 m 高度作为参考点(40 m 高度的风速风向相对稳定准确),则在t1时刻,测风塔40 m 高度处参考点风速Uc,40−1即为参考归一化风速,将此后任意高度测量点的测量时刻称为t2时刻,则t2时刻z高度处基于无人机所测的风速表示为Uw,z−2,t2时刻测风塔40 m 高度处参考点的风速表示为Uc,40−2,由此,无人机在z高度处相对t1时刻的归一化风速Uw,z为:

利用归一化后的10 m~100 m 风速来进行风剖面拟合(如图6所示为其中一组的拟合结果),由图6可见实测值的拟合较好,且其拟合表达式在图中给出,粗糙度α 为0.147。同时表4中记录了不同时间各组实测值的拟合相关系数R2值,亦可见各组的拟合精度较高,并且随着风速的增大,R2值增大,说明风速越大,各高度所测的风速越稳定准确。将实测拟合曲线与中国规范B类地貌,美国规范C类地貌,欧洲规范Ⅱ类地貌及澳大利亚规范B类地貌[13−16]的风剖面曲线进行对比,其中中国规范与美国规范采用指数率模型,欧洲规范及澳大利亚规范采用对数率模型,由图6可知实测拟合曲线与中国规范B类地貌风剖面最为接近。

图6 风剖面拟合(B类地貌)Fig.6 Wind profile fitting (Type B geomorphology)
利用指数率模型拟合计算地面粗糙度 α,表4记录了在不同时间、不同平均风速下拟合得到的地面粗糙度及置信区间,分析所测数据,数据基本稳定在0.137~0.156,范围为0.019,均值为0.148。从地貌来看,西南西北方向虽然有低矮房屋但是大部分不超过9 m,因此值约为0.15,由此判断该地貌为B类地貌是合适的。图7则给出了粗糙度与风速的关系,由图中趋势可知,随着风速的增大,所拟合的地面粗糙度的离散性有所减小,产生的原因是随着风速的增大,各高度所测的风速更稳定且准确,则计算得到的地面粗糙度结果偏差更小,离散性减小。
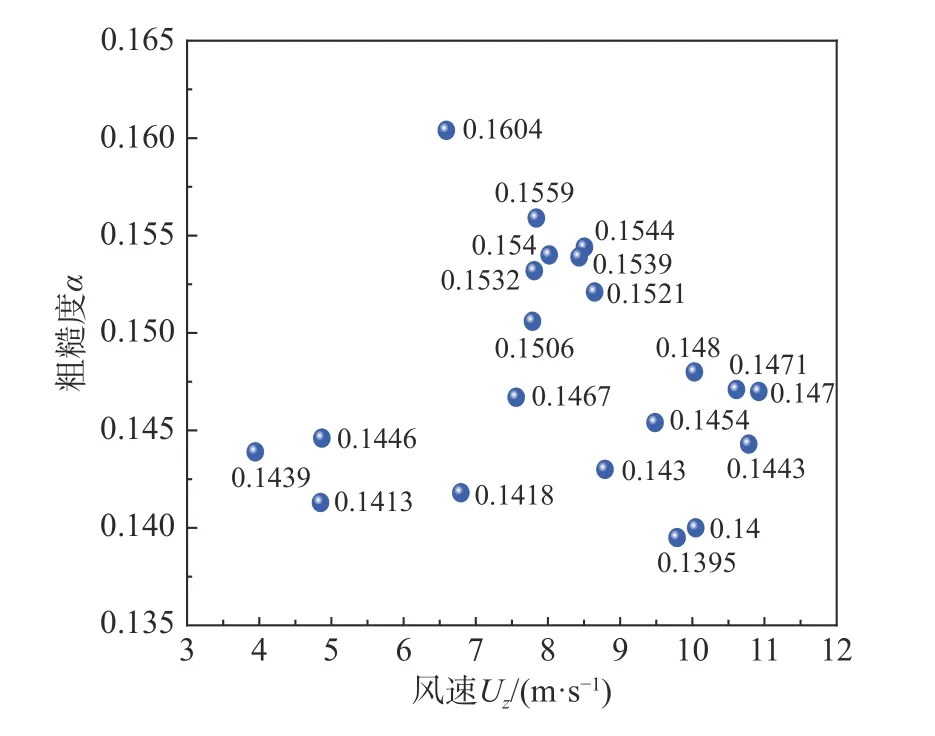
图7 地面粗糙度αFig.7 Ground roughnessα

表4 地面粗糙度拟合Table 4 Ground roughness fitting
3.2 脉动风特性
脉动风特性参数包括湍流度、阵风因子、湍流积分尺度及脉动风速功率谱等,其中基于无人机与测风塔所测的湍流度均由式(8)计算得出,两者阵风因子根据式(9)计算得到,湍流积分尺度则根据式(10)得出。
表5记录了10 m~40 m 的4个高度处基于无人机与测风塔所测顺风向湍流度均值、顺风向阵风因子均值和顺风向湍流积分尺度均值的统计结果及两者对比结果。可知,10 m~40 m 各高度处基于无人机所测的顺风向湍流度平均值表现出与测风塔的对应数值近似一致的特性,由表5中测量组中的最大误差组可以发现各高度上两者最大误差控制在±5%以内,由此可见,基于无人机所测的湍流度能够较为准确真实地反映测风塔所测湍流度。同样,基于无人机所测顺风向阵风因子均值与测风塔所测值也较为接近,且变异系数较小(均小于0.1),数据较为稳定;基于无人机所测顺风向湍流积分尺度均值与测风塔所测均值对比误差控制在±4%内,最大误差值在±5%以内。可见无人机能够较为真实准确地反映测风塔的实测结果,证实了其测量脉动风特性的可行性。

表5 无人机与测风塔风场参数对比Table 5 Comparison of UAV and wind tower wind field parameters
表6给出了无人机在10 m~100 m 范围内的10个高度处所测得的顺风向和横风向各项湍流参数的均值,同时给出测风塔在10 m~40 m 范围内4个高度处所测得的对应数据的均值进行比较。由表6可知,随着高度的增加,无人机所测顺风向湍流度Iw,u及横风向湍流度Iw,v均表现为减小趋势,另外Iw,u/Iw,v在1∶0.82~1∶0.88,与我国桥梁抗风设计指南规定的1∶0.88 接近,较为准确地反映了良态风的湍流特性。同样,顺风向阵风因子Gw,u及横风向阵风因子Gw,v也随着高度的增大而减小;而顺风向与横风向湍流积分尺度则是随高度增加而增大,且10 m~100 m 范围内Lw,u/Lw,v在1∶0.68~1∶0.75,这与文献[22]的比值接近,说明该测点处10 m 范围内与10 m~100 m 范围内的湍流积分尺度的比值差异不大。

表6 不同高度脉动风特性参数Table 6 Pulsating wind characteristic parametersat different heights
图8(a)给出了基于无人机所测顺风向湍流度与风速的变化关系(由于篇幅原因只给出顺风向参数,横风向的结论与顺风向相同),可知各高度处顺风向湍流度随着风速的增大呈减小的趋势,这是由于大气稳定性随风速增大而增加,从而减小了湍流度[23];图8(b)给出基于无人机所测顺风向阵风因子与风速的变化关系,可以看到各高度的阵风因子均随着风速的增大而减小;图8(c)则给出了基于无人机所测顺风向湍流积分尺度与风速的变化关系,可见随着风速的增大,各高度的湍流积分尺度都呈现增长趋势。

图8 顺风向各项湍流参数随风速的变化Fig.8 Changesof turbulence parameterswith wind speed
3.2.1湍流度与阵风因子
湍流度与阵风因子之间存在一定相关性,一般认为湍流度越大,阵风因子也越大。多年来,人们对湍流强度与阵风因子的关系进行了研究,Ishizaki[24]和Choi[25]分别提出的公式可以组合成一个方程式(15)来表示湍流强度和阵风因子之间的关系:
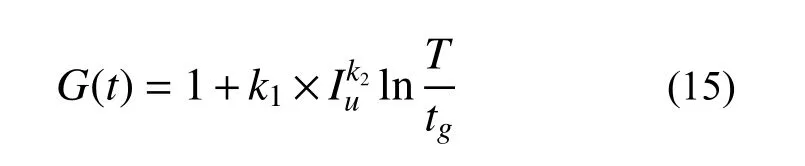
式中:T为平均时距;tg为阵风持续时间;k1、k2为无量纲参数,其中Ishizaki[24]建议k1=0.5,k2=1.0,Choi[25]建议k1=0.62,k2=1.27。图9给出了40 m高度处湍流度与阵风因子的相关性,利用式(15)对基于无人机所测的各高度处的数据进行拟合,拟合结果与Ishizaki和Choi的经验表达式一起给出,所得k1=0.49,k2=0.98,并且在其他高度上,10 m 高度处k1=0.51,k2=0.99;20 m 高度处k1=0.53,k2=1.00;30 m 高度处k1=0.49,k2=0.95,这与Ishizak 拟合的曲线非常接近,说明阵风因子随湍流强度呈近似线性增长的趋势。
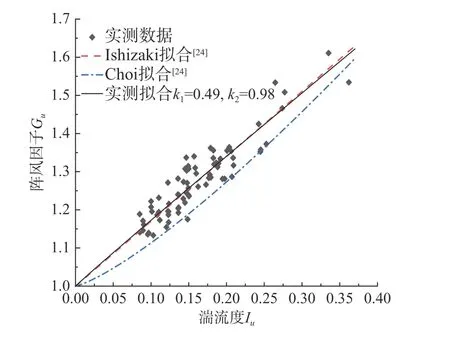
图9 湍流度与阵风因子相关曲线Fig.9 Turbulence and gust factor correlation curve
3.2.2湍流度剖面及湍流积分尺度剖面
由于无法在同一时间测得各个高度的湍流度及湍流积分尺度,因此湍流度剖面及湍流积分尺度剖面的各高度均值与平均风速剖面中的计算相似,为了反映同一时间各高度处的湍流度及湍流积分尺度情况,利用式(16)和式(17)将所得值进行转换:
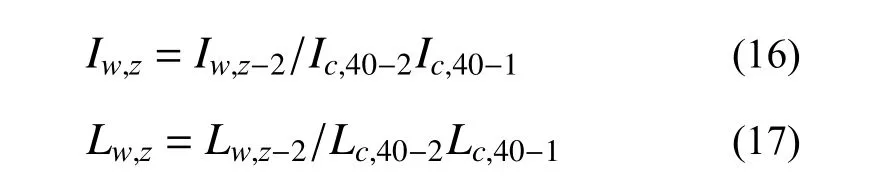
式中:Iw,z为最终所得同一时间下各高度处无人机所测湍流度;Ic, 40−1为t1时刻测风塔40 m参考点湍流度;Iw,z−2为t2时刻z高度处无人机测得的湍流度;Ic,40−2为t2时刻参考点的湍流度。同理,式中Lw,z为最终归一化的湍流积分尺度,Lc, 40−1为t1时刻测风塔参考点湍流积分尺度,Lw,z−2为t2时刻z高度处无人机测得的湍流积分尺度,Lc,40−2为t2时刻参考点的湍流积分尺度。
图10给出了基于无人机所测的顺风向湍流度均值随高度的变化关系及湍流度剖面的拟合。由图8可知湍流度与风速相关,随着风速增大湍流度呈减小趋势,因此根据图8的分布将风速分成3个风速段来进行湍流度剖面的拟合,分别是4 m/s~6 m/s风速段、6 m/s~8 m/s风速段、8 m/s~10 m/s风速段,结果在图10中呈现。图10中还给出了同地貌条件(B类地貌)及高度下的中国、美国、日本及欧洲规范中的湍流度剖面,由图可知各风速段顺风向湍流度均值的拟合较好,而拟合曲线与各国规范都有差异,较中国规范偏大,而相对于美国、日本及欧洲规范数值偏小。通过式(16)换算后的湍流度变异系数较大,经分析,由于不同高度的脉动风特性较平均风特性的差异性更大,即t2时刻Iw,z-2与Ic,40-2相关性较低,因此在利用式(16)时Iw,z-2/Ic,40-2比值关系将产生一定误差,导致得到的归一化湍流度也会产生误差。

图10 顺风向湍流度随高度变化Fig.10 Downwind turbulence variation with altitude
图11(a)给出了基于无人机所测的顺风向湍流积分尺度均值与高度的变化关系。同样将风速分成3段进行拟合,并与同地貌条件下(B类地貌)各国规范进行对比。由图可知湍流积分尺度的数值大小相比于各国规范都要小,初步分析可能原因是测量时距较短,而根据Yu 等[26]的研究,随着实测时距的减小,湍流积分尺度会减小,并存在如式(18)的关系:

式中:T表示测量时距。将实测数据按式(18)转换为10 min 时距相对值,得到图11(b)中的修正后的湍流积分尺度剖面,发现在修正后不同风速段的湍流积分尺度有一定差异,总体均值可以认为与日本规范较为接近。误差的产生可能是由于时距对湍流积分尺度的影响仍然存在,且式(17)存在与式(16)相似的计算误差,另外场地与风场的不同对湍流积分尺度的修正也有较大影响。

图11 顺风向湍流积分尺度随高度变化Fig.11 Turbulence integral scale variation with height
3.2.3脉动风速功率谱密度函数
脉动风速功率谱密度函数根据式(11)计算,其中Davenport 谱不随高度变化,而Kaimal谱和Karman 谱与高度相关。本文选取了多组10 m~40 m 无人机与测风塔在时距为10 min 下测量得到的强风时程样本进行脉动风速功率谱的拟合,得到了4个高度处顺风向脉动风速的归一化功率谱。由于Kaimal 谱和Karman 谱与高度相关,因此将测风塔10 m~40 m 各高度实测值的顺风向脉动风速功率谱依次单独绘出并与经验谱进行比较如图12(a)~图12(d)所示,由图可见,10 m 高度处实测值的顺风向脉动风速功率谱由于湍流较大,与各经验谱的拟合都相对较差;而20 m~40 m 各高度实测值的顺风向脉动风速功率谱与Karman 谱的拟合较好。
图13则给出了在30 m 及40 m 高度处由无人机与测风塔实测值拟合的顺风向脉动风速功率谱密度函数,由图可知,无人机所拟合的结果与同高度及时距下的测风塔的拟合结果总体上较为吻合,在部分频率段下稍有差异,高频段无人机拟合的功率谱密度函数波动稍大但仍与测风塔拟合的函数有一致的趋势,再将无人机与测风塔所拟合的脉动风速功率谱与经验谱进行对比,同样发现实测值拟合的顺风向脉动风速功率谱与Karman谱有较高的一致性。图14则给出了40 m 以上的4个高度上基于无人机所测得的顺风向脉动风速功率谱密度函数,由图可知各高度处实测值拟合的顺风向脉动风速功率谱均与Karman 谱的一致性最高,这也说明基于无人机实测所拟合的各高度处的脉动风速功率谱密度函数有较高的真实性与准确性,但是无人机仍无法像测风塔在图12(a)中一样,在同一时间反映不同高度处的结果。

图12 10 m~40 m 测风塔顺风向脉动风速功率谱Fig.12 Measured power spectra of fluctuating wind speed along wind direction of 10 m~40 m wind tower

图13 无人机及测风塔顺风向脉动风速功率谱Fig.13 Measured power spectra of fluctuating wind speed along wind direction of UAV and wind tower


图14 50 m~100 m 无人机顺风向脉动风速功率谱Fig.14 Measured power spectra of fluctuating wind speed along wind direction of 50 m~100 m wind tower
4 结论
本文对比了北京延庆实验基地的测风塔风速仪实测数据及六旋翼无人机搭载风速仪的实测数据,对多旋翼无人机的边界层风场实测的可行性进行了研究,经分析得到以下结论:
(1)无人机实测平均风速与测风塔的实测平均风速存在一定差异,但通过对无人机所测风速时程进行修正,可得到与测风塔所测结果相近的数据,且两者误差较小(±3%以内)。
(2)利用无人机所测各高度处归一化后的平均风速拟合的风剖面拟合精度较高,数据离散小(R2>0.87),且与我国规范B类地貌的风剖面接近;拟合得到的地面粗糙度均值为0.148,接近规范标准值0.15,并判断该地为B类地貌。
(3)由无人机风场实测数据计算所得的湍流度及阵风因子与由测风塔实测数据计算所得结果接近,误差均在±5%以内,且随着高度或风速的增大,湍流度及阵风因子均逐渐减小;基于无人机所测得的湍流度剖面受时距及换算误差的影响与各国规范均有差异,较中国规范偏大,而相对于美国、日本及欧洲规范数值偏小;湍流度和阵风因子之间存在指数关系,阵风因子随湍流度的增大而增大,拟合结果与Ishizak 拟合曲线接近。
(4)由无人机风场实测数据计算所得的湍流积分尺度与由测风塔实测数据计算所得结果接近,并与风速、高度均呈正相关。各风速段的湍流积分尺度随高度的变化关系有一定差异,总体与日本规范较为接近。
(5)由无人机风场实测数据拟合的脉动风速功率谱与同高度及时距下测风塔实测数据拟合的脉动风速功率谱基本一致,在高频部分稍有差异,且10 m~100 m 各高度所测脉动风速功率谱与经验谱Karman 谱均较吻合。

