高强钢管高强混凝土徐变特性试验研究

黄永辉，刘爱荣，傅继阳，朱书汉，饶 瑞

(广州大学风工程与工程振动研究中心，广东，广州510006)

钢管混凝土(CFST)是一种极具潜力的组合结构形式，其充分结合了钢材和混凝土的优点。目前，随着工艺进步和各种硅灰、添加剂的使用，强度大于100 MPa 的高强混凝土的制备越发容易，然而高强混凝土由于脆性大，不能直接应用于建筑与桥梁结构[1−2]，为了增加其延性，可将高强混凝土与高强钢管进行组合，形成高强钢管高强混凝土(HS-CFST)，充分利用高强钢管的约束作用，使核心混凝土具有一定的延性，从而满足结构使用性能的要求[3]。徐变是混凝土的重要特性，将导致混凝土结构的长期变形，并会对钢管混凝土结构产生重大的应力重分布影响[4−6]。目前，国内外很多学者对钢管普通混凝土的收缩和徐变特性进行了大量的试验研究。其中，Terrey等[7]、Uy[8]和Kwon 等[9]进行了钢管混凝土试件的收缩和徐变试验，并采用ACI209徐变预测模型与试验结果进行了对比分析。Vandewalle[10]进行了变温变湿环境的混凝土收缩和徐变特性试验研究，重点研究了温湿度变化对徐变的影响。Yang等[11]进行了9个钢管普通混凝土和3个素混凝土试件分别在3种不同应力水平下的收缩和徐变试验，实测了1710 d 的实测数据，并在试验结果的基础上对ACI209徐变模型进行了修正。Wang等[12]依托北盘江大桥工程，实测了该大桥所用钢管混凝土的收缩和徐变特性，并基于试验结果，对MC2010徐变模型进行了修正。还有部分学者对钢管再生骨料混凝土[13]、钢管膨胀混凝土[14]、钢管粉煤灰混凝土等[15]的收缩和徐变特性进行了试验研究。彭建新等[16]推导了钢管混凝土拱肋应力重分布计算公式，王玉银等[17]对5种常用的钢管混凝土收缩和徐变模型及3种常用的计算方法进行了对比分析，丁敏等[18]提出了适用于钢管混凝土轴心受压构件的徐变预测模型-Huo模型。曹万林等[19]对11个配筋再生混凝土棱柱体试件进行了长期轴压荷载下的徐变试验，研究了再生骨料取代率配筋对混凝土徐变特性的影响。

针对高强钢管高强混凝土的收缩和徐变特性，Ma 和Wang[20]进行了8个高强钢管混凝土试件的徐变试验，实测了380 d 的徐变数据，基于B3模型提出了高强钢管混凝土的徐变预测模型。Farhad[21]基于徐变试验数据库的结果，对比分析了普通和高强自密实混凝土的徐变特性，并提出了徐变预测模型。Pan 等[22]评估了几种常用徐变模型如ACI 209-92[23]、JTG D62−2004[24]、B3[25]和GL 2000[26]的适用性，并在JTG D62−2004[24]徐变模型的基础上提出了一种修正模型。

综上，国内外关于高强钢管高强混凝土收缩和徐变特性的研究并不多见，由于高强混凝土的配合比与普通混凝土存在较大差异，既有的钢管普通混凝土的收缩和徐变试验结果和徐变模式能否推广应用于高强钢管高强混凝土还存在不确定性。为此，本文将进行高强钢管高强混凝土轴压短柱试件的收缩和徐变试验，实测其徐变变化规律，通过将现有的徐变预测模型的理论计算结果与试验结果进行对比，比选出适用于高强钢管高强混凝土最优的徐变预测模型，从而为研究高强钢管高强混凝土拱桥的时变力学行为提供依据。

1 混凝土收缩和徐变模型

1.1 素混凝土的收缩和徐变预测模型

国内外现有常用的素混凝土徐变预测模型主要包括如下几种：MC90模型[27]、ACI209模型[23]、B3模型[25]、GL2000模型[26]、MC2010等[28]。其中MC90模型[27]和ACI209模型[23]应用最为广泛，而MC2010模型[28]将徐变分为基本徐变和干燥徐变，特别适用于钢管核心混凝土。因此本文主要采用MC90模型[27]、ACI209模型[23]和MC2010模型[28]与试验结果进行对比分析。

1.2 钢管混凝土的收缩和徐变预测模型

对于钢管约束的核心混凝土，其工作环境与素混凝土主要存在以下2点不同：一是核心混凝土被钢管所密封，其无法与外部进行湿度的交换，也就不存在干燥收缩与干燥徐变；二是核心混凝土被钢管所约束而无法自由的变形，这也将导致混凝土和钢管的内力重分布，即钢管的应力变大，混凝土的应力变小，从而导致核心混凝土的徐变变小。因此，上述素混凝土的收缩和徐变预测模型无法直接用来预测钢管混凝土的收缩和徐变。

为了考虑钢管混凝土的密封性，通常的做法是在徐变模型计算时将相对湿度取一个大值，根据文献[29]的试验研究结果，一般取值为RH>95%。另外，如果徐变模式将徐变分为基本徐变和干燥徐变，则可以直接将干燥徐变取为0，从而只考虑基本徐变的影响。为了考虑钢管的约束作用，可以通过内力平衡条件，建立钢管和混凝土的变形协调方程来考虑其内力重分布的影响[30]。其中最常用的方法有2种[31]：一是按龄期调整的有效模量法(AAEM)；二是逐步积分法(Step-by-Step)。这两种方法各有优缺点，AAEM 是一种代数的方法[32]，其可以理论推导徐变变形的解析表达式，便于工程设计。而逐步积分法精度更高，但需要编程实现，不利于设计和规范采用。为此，本文采用AAEM 计算钢管混凝土的收缩和徐变系数表达式。文献[33]的研究结果表明，AAEM的计算精度与逐步积分法误差并不大。

当采用AAEM 法进行钢管混凝土的收缩和徐变计算时，其徐变系数表达式如下[32]：

2 收缩和徐变试验

2.1 模型设计

本次试验一共设计了4组共15 个模型，其中A0 组为素混凝土模型，包括2个高强素混凝土徐变模型和1个收缩模型；A1～A3组分别为含钢率8%、10%、12%的高强钢高强混凝土模型，分别包括3个高强钢高强混凝土徐变模型和1个收缩模型。钢管的外径为140 mm，钢管壁厚分别为2.5 mm、3.2 mm 和4 mm，试件高度为320 mm。加载试件的核心混凝土应力水平即施加的长期荷载与极限荷载的比值为0.30，试件的极限荷载通过轴压短柱的承载力试验得到。试验模型参数见表1。

表1 收缩和徐变试验模型参数表Table 1 Details of creep and shrinkage experiment specimens

2.2 材料参数

高强钢材采用Q560钢材，通过材性试验实测得到的钢材屈服强度为560 MPa，极限强度为688 MPa，弹性模量为220 GPa，泊松比为0.292，延伸率为29.0%。

核心混凝土28 d 立方体强度为106.3 MPa，配合比如表2所示，实测得到的混凝土力学特性如表3所示。

表2 试验混凝土配合比/(kg/m3)Table2 Concretemixing proportion for testing

表3 混凝土力学性能实测值Table 3 Tested mechanical propertiesof concrete

2.3 收缩和徐变测试装置

试验加载设备采用北京仪创YC-XB100S型混凝土徐变仪，如图1所示。加载装置由3根大直径螺杆，上、中、下3块加载钢板，压力传感器和底部弹簧组成。该装置最大加载能力为1000 kN，通过电动千斤顶施加荷载，所施加的荷载由压力传感器通过读数仪实时显示。底部弹簧的恢复力可以有效消除由于徐变变形导致的力的卸载。

图1 混凝土徐变试件和加载装置Fig.1 Specimensand testing instrumentations

在钢管表面前、后、左、右4个方向对称布置振弦传感器和应变片采集钢管应变，在核心混凝土的中央预先埋入振弦传感器用于测试混凝土应变。应变测点布置示意图如图2所示。表面式振弦传感器采用北京基康的BGK-4000x 传感器，埋入式振弦传感器采用北京基康的BGK-4200x 传感器，应变花采用日本TML 公司生产的型号为FCA-3-11-3LJBT双轴应变花。

图2 应变测点布置图 /mmFig.2 Arrangement of strain measuring points

试验中电阻应变片采用扬州晶明JM3813静态应变采集仪进行数据采集，每台应变采集仪60个通道。振弦传感器采用扬州晶明JM3818A 频率采集仪进行。JM3813与JM3818A 均自带有蓄电池和存储卡，可以在断电情况下连续工作48 h，保证了测试的连续性。试验在恒温的实验室进行，通过空调将温度控制在20℃ ± 2℃以内，湿度控制在50%～70%，尽量消除温湿度的影响。

3 试验结果和分析

3.1 收缩应变

图3(a)为4个收缩试件的收缩应变随时间的变化曲线，由图可知，素混凝土的收缩应变远大于钢管混凝土的收缩应变，当加载365 d 后，素混凝土的收缩应变约为钢管混凝土的3倍。无论是素混凝土还是钢管混凝土，收缩应变只是在早期增加的非常迅速，而随着时间增加，增速越来越慢，加载200 d 后，钢管混凝土的收缩已基本稳定，但是素混凝土的收缩还在持续增加。图3(b)为3个不同含钢率钢管混凝土试件的收缩应变随时间的变化曲线，由图可知，含钢率对钢管混凝土的收缩基本无影响，当加载365 d 后，含钢率分别为8%、10%、12%的试件的收缩应变分别为21µε、20µε 和19µε，几乎相等。这主要是因为：1)由于钢管的密封作用，核心混凝土与外部环境没有水分的交换，其收缩值非常小，导致其差距不明显；2)三个试件的含钢率差异不大，难以对钢管混凝土的收缩产生明显影响。

图3 实测收缩应变-时间曲线Fig.3 Experimental shrinkagestrain vs.time

3.2 徐变应变和徐变系数

素混凝土和钢管混凝土的徐变应变随时间的变化曲线如图4所示，在这些曲线中均减去了相应的收缩应变。由图可知：1)钢管混凝土和素混凝土的徐变具有相同的趋势，徐变应变均随着时间的增加而增加，且早期增加速度较快；2)钢管混凝土的徐变应变远小于素混凝土，当加载365 d后，A0组(素混凝土)、A1、A2和A3(钢管混凝土)组的平均徐变应变分别为464µε、214µε、221µε 和194µε，钢管混凝土的徐变应变小于素混凝土的1/2；3) A2组3个试件徐变应变的离散性较大，这主要是因为加载偏心导致。同一组中3个试件为层叠放置，加载时偏心难以避免，若偏心较大则实测应变的离散性也较大。综合三组试件结果可知，A2组的偏心更为严重，但通过对3个试件取平均值，可有效消除偏心的影响。

图4 实测徐变应变-时间曲线Fig.4 Experimental Creep Strain vs.Time

将徐变应变除以试件加载时刻的初始弹性应变即可得到试件的徐变系数，如图5所示。由图可知，徐变系数曲线的变化规律与徐变应变一致，在加载早期徐变系数快速增加，而后期增长缓慢。

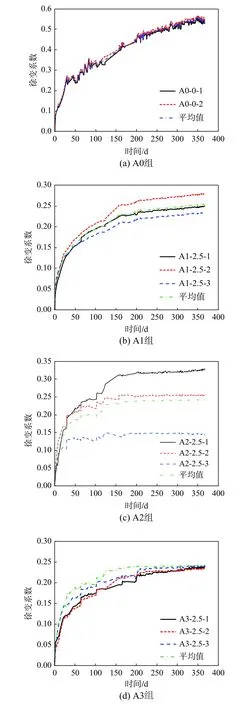
图5 实测徐变系数-时间曲线Fig.5 Experimental creep coefficient vs.time

钢管混凝土与素混凝土的徐变系数对比如图6(a)所示，由图可知，钢管混凝土的徐变系数远小于素混凝土，当加载365 d 后，A0、A1、A2和A3组的平均徐变系数分别为0.554、0.256、0.243和0.239，钢管混凝土的徐变系数小于素混凝土的1/2。

不同含钢率钢管混凝土试件的徐变系数对比如图6(b)所示，由图可知，徐变系数随着含钢率的增加而减小，这与理论公式是一致的，可由式(1)直观看出。但由于本次试验模型的含钢率差异不大，导致各曲线的差异不明显。

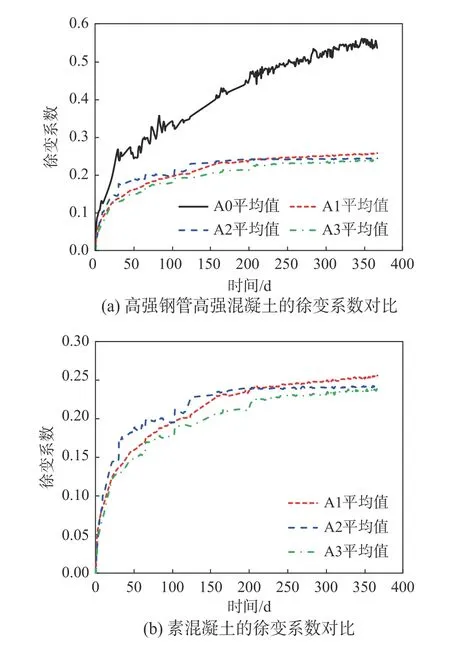
图6 高强钢管高强混凝土与素混凝土徐变系数对比Fig.6 Comparison of the creep coefficient between HS-CFST and plain concrete

3.3 试验结果和规范模型的对比

本文将试验结果与MC90模型[27]、ACI209模型[23]和MC2010模型[28]的预测结果进行对比。在这3种徐变模型中，需要用到的设计参数如表4所示。由于钢管的密闭作用，相对湿度RH取为99%，fcm为混凝土平均抗压强度。模型预测结果为按式(1)修正后的结果。

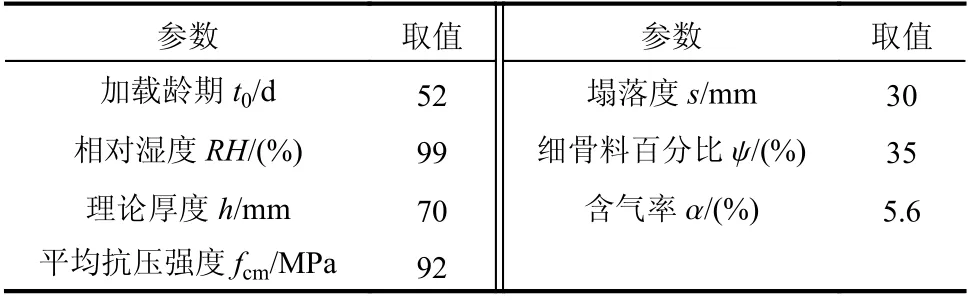
表4 徐变模型计算参数Table 4 The parametersfor thecreep models

图7为试验结果与3种徐变预测模型计算结果的对比。由图可知：1)无论是试验结果还是预测结果均表现出同样的规律，即徐变在开始加载阶段增长较快，随着时间的增加而变得平缓；2)无论是素混凝土还是钢管混凝土，在这3种徐变预测模型中，MC2010模型[28]与实测结果吻合最好，其次为MC90模型[27]，ACI209模型[23]的预测结果误差最大。MC90模型[27]和ACI209模型[23]均高估了素混凝土和钢管混凝土的徐变，因此在工程设计中推荐采用MC2010模型[28]来预测素高强混凝土及高强钢管高强混凝土的收缩和徐变。

图7 试验结果与模型预测结果对比图Fig.7 Comparison between experimental resultsand predicted onesfrom existing models

4 徐变特性对比研究

为了对比高强钢管高强混凝土与普通钢管混凝土收缩和徐变特性的不同，同时还进行了C30钢管混凝土和C50钢管混凝土短柱的徐变试验，实测了365 d 的收缩和徐变值。普通钢管混凝土徐变试件的参数如表5所示，其中钢管采用的是Q235普通钢材，钢管厚度分别为5 mm、6 mm 和7 mm这3种，其他尺寸参数与高强钢管高强混凝土试件相同。

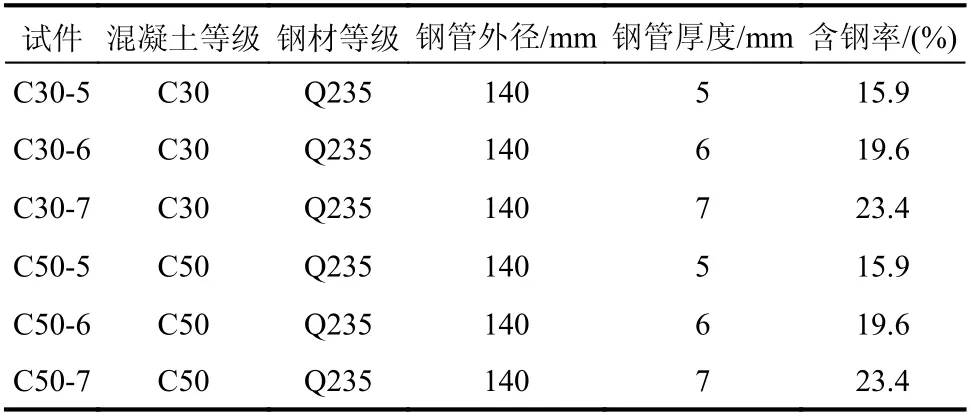
表5 普通钢管混凝土收缩和徐变试验参数Table5 Parametersof creep and shrinkage experiments of N-CFST specimens

图8为C30钢管混凝土和C50钢管混凝土的实测徐变系数随时间的变化曲线。由图8可知：1)普通钢管混凝土与高强钢管高强混凝土的徐变系数呈现相同的规律，即徐变在加载初期增长较快，后期变得平缓，加载200 d 后，混凝土的徐变开始稳定，前60 d 的徐变值达到了365 d 徐变值的70%；2)钢管混凝土的徐变随着含钢率的增加而减小，3种不同含钢率试件的徐变系数曲线之间差别非常明显；3)徐变系数随着混凝土强度的增加而减小，相同设计参数下，C50钢管混凝土的徐变系数比C30钢管混凝土的徐变系数小约10%。

图8 普通钢管混凝土实测徐变系数曲线Fig.8 Experimental creep coefficient vs.time of normal CFST

为对比普通钢管混凝土与高强钢管高强混凝土收缩和徐变的异同，选用普通钢管混凝土的C30-5和C50-5试件与高强混凝土的A3(C105-4)试件进行对比分析。这3组试件的含钢率基本一致，其中C30-5和C50-5的含钢率为15.9%，C105-4的含钢率为12%。徐变系数的对比曲线如图9所示，试验参数如表6所示。由图9可知：3组试件的徐变系数曲线存在明显的区别，混凝土的徐变随着强度的提高而减小。加载365 d 后，C30-5、C50-5、A3(C105-4)的徐变系数分别为0.271、0.254和0.239。需要说明的是，C30-5、C50-5和A3(C105-4)的加载龄期和含钢率并不完全一致。如果C105-4试件的加载龄期由52 d 改为75 d，则其徐变将随着加载龄期的增大而减小；如果C105-4试件的含钢率由12.0%改为15.9%，则其徐变将随着含钢率的增大而进一步减小。因此如果所有参数都一致，C105钢管混凝土的徐变系数曲线与C30-5、C50-5的区别将会更加明显。这主要是因为高强混凝土的配合比和普通混凝土相比存在明显差异，高强混凝土的水灰比远小于普通混凝土，导致其徐变偏小。

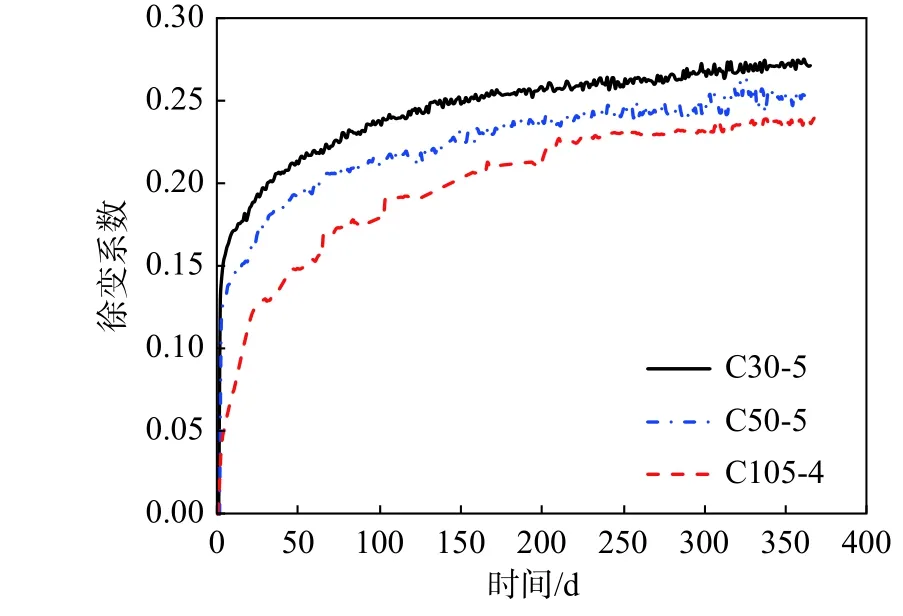
图9 HS-CFST和N-CFST的徐变系数曲线对比Fig.9 Creep coefficient comparison of HS-CFST and N-CFST

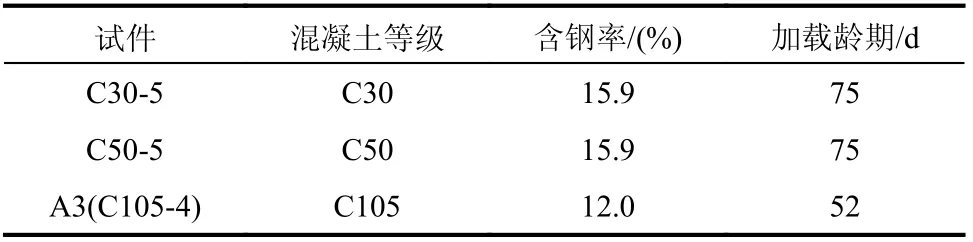
表6 高强钢管高强混凝土和普通钢管混凝土试件设计参数Table 6 Parametersof HS-CFST and N-CFST specimens

5 结论

本文对高强钢管高强混凝土的收缩和徐变展开了试验研究，将试验结果与现有的常用徐变预测模型MC90模型[27]，ACI209模型[23]和MC2010模型[28]的预测结果进行了对比，同时对比分析了高强钢管高强混凝土和普通钢管混凝土徐变系数的差异，研究结果表明：

(1)钢管混凝土试件的收缩特性和素混凝土试件有明显不同。素混凝土试件的收缩应变远大于钢管混凝土试件的收缩应变，在加载365 d 后，素混凝土的收缩约为钢管混凝土的3倍。

(2)钢管混凝土试件的徐变特性与普通混凝土试件有明显不同。由于钢管的密封和约束作用，钢管混凝土的徐变远远小于普通混凝土试件的徐变，在加载365 d 后，普通混凝土的徐变系数是钢管混凝土徐变系数的2倍以上。含钢率对钢管混凝土试件的徐变有一定的影响，徐变系数随着含钢率的增加而减小。

(3)将试验结果与现有的常用徐变预测模型MC90模型，ACI209模型和MC2010模型的预测结果进行对比分析，结果表明无论是钢管混凝土试件还是素混凝土试件，采用MC2010模型预测的徐变曲线与实测结果吻合最好，其次为MC90模型，ACI209模型的预测结果误差最大。因此在工程设计中建议采用MC2010模型来预测素高强混凝土以及高强钢管高强混凝土的收缩和徐变。

(4)进行了C30和C50普通钢管混凝土试件的徐变试验，并将其与C105高强钢管混凝土试件的徐变结果进行了对比。结果表明，钢管混凝土的徐变与混凝土的强度负相关，钢管混凝土的徐变随着混凝土强度的增加而减小，不同混凝土强度试件的实测徐变曲线存在明显区别。这主要是因为，高强混凝土的配合比和普通混凝土相比存在明显差异，高强混凝土的水灰比远小于普通混凝土，导致其徐变偏小。