基于计算机视觉人行桥挠度影响线非接触式识别

朱前坤，陈建邦，张 琼，杜永峰

(兰州理工大学防震减灾研究所，兰州730050)

人行桥因其轻质高强及视觉效果优美等特点，常被建造于城市交通网络和各大景区，保持人行桥的安全运行对避免人、车流相交冲突和维持正常交通具有重要意义。在日常使用和其他外部因素的影响下，桥梁结构不断发生变化、退化和损伤，损伤识别是结构健康监测的重要组成部分[1−2]及核心技术。

为了全面、充分地评价结构性能，估计结构损伤状态、结构安全性和预测结构剩余使用寿命，需要对结构的荷载输入和响应输出进行监测。基于影响线的损伤检测方法一经发明便迅速发展[3−6]。周建庭等[7]采用递推迭代法实测桥梁影响线，通过多工况的静载试验，达到实际荷载检测桥梁的目的。静载试验需要长时间中断交通，测试成本高，且获取的数据量有限，在实际应用中具有局限性。徐文涛等[8]通过虚拟激励法计算桥梁在行驶车辆和桥面不平度共同作用下的随机响应，获得了桥梁跨中挠度的动态影响线值。通过结构输入输出反算得到的影响线实质上是单位荷载下的动力响应，未充分体现影响线准静态特性，故需对计算影响线进行处理[9]。Ieng[10]提出了影响线识别的最大似然估计方法。Sun 等[11]采用有限元模型修正实测桥梁影响线。Wang 等[12]采用分段多项式拟合实测桥梁影响线进而得到具有准静态特性的影响线。上述研究使用传统传感器进行结构输入输出监测，使用传统传感器的缺点是封闭交通、安装时间长和布线工作需要大量劳动力。

集成多学科的优势，国内外学者研究了各种先进的传感技术，如用于动态监测的无线传感器[13]和基于视觉识别技术的全桥梁监测[14]等已被应用于当前的研究和实践中。在这些技术中，基于视觉的方法越来越受到结构健康监测领域的关注。Tian 等[15]在实验室对简支梁进行冲击试验，使用相机捕捉人体输入得到人致冲击力，使用加速度传感器收集响应输出，以此识别桥梁更多模态参数，并对人行天桥进行了冲击试验验证，提取了频率、振型和比例因子等模态参数。随后Tian 等[16]通过移动单个相机测量结构的多点位移直接获得大型结构的结构属性，提高桥梁结构的测试效率，并从移动冲击测试数据中识别出更多的结构特性。上述文献将研究重心集中在结构输入输出数据和结构动力特性上，通过相机和传统传感器相结合进行。Zaurin 和Catbas[17―18]将视觉识别技术和传统传感器(如应变计)结合起来，通过确定的额定荷载提取应变单位影响线，并统计数据异常值检测识别损伤。Khuc和Catbas[19]集成了计算机视觉和位移传感器，以获得位移单元影响面，并提出了一种检测桥梁损伤的统计方法。上述研究提取了静态结构特性作为损伤特征，并使用视觉识别技术进行结构输入估计，使用传统传感器进行结构输出监测，未能克服传统传感器的不足。

本文将便携式相机与无线传感器相结合，开发了一种完全非接触式影响线识别系统，克服了使用传统传感器的不足。将便携式相机获得行人位置信息与无线传感器测得的行人竖向加速度相结合作为结构输入。将便携式相机与视觉识别技术得到的结构位移响应作为结构输出。根据结构输入输出数据反算人行荷载作用下桥梁挠度影响线。然后利用多项式分段拟合初始实测人行桥挠度影响线，进而得到具有准静态特性的挠度影响线，可为结构工程师准确高效地提供桥梁损伤检测依据。

1 挠度影响线数学模型

桥梁在正常使用过程中受温度、湿度及风荷载等可变荷载引起的响应不会发生突变，因此相较于人群荷载，可以忽略短时间内温度、湿度及风速等变化对人行桥变形的影响。为了计算方便，将桥上人群荷载简化为对应人体质心处的竖向力，则桥梁受人行荷载引起的位移响应可视为一个竖向力引起的响应。单个行人随顺桥向位置变化所引起测量位置的位移响应可表示为[17]：

式中：d为包含由行人荷载在选定位置引起的响应向量；w为包含与行人移动位移相关的荷载矩阵；u为挠度影响线向量。式(1)可以改写为：

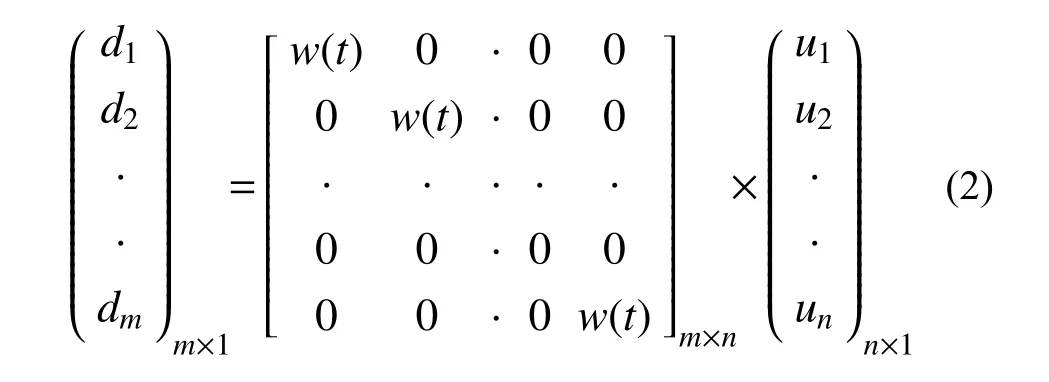
式中：n为行人沿桥移动步骤的离散系数数量；m为位移响应的测量样本数量；w(t)为不同时刻单个行人的竖向人行荷载，可用式(3)计算[20−22]：

即可通过已知的荷载输入和响应输出求解影响线。从试验出发，基于行人荷载位置和人行荷载数据结合结构位移响应数据进行影响线识别。

2 挠度影响线视觉提取方法

本文通过对便携式相机获取的图像进行行人检测跟踪，并估计出行人的位置，结合无线传感器确定人行荷载组成结构输入数据。将视觉测量的桥梁位移响应视为结构输出数据，利用结构输入输出数据反算挠度影响线，流程图如图1所示。下面分别介绍了基于视觉的行人位置估计方法和基于视觉的结构位移测量方法。

图1 计算挠度影响线流程图Fig.1 Flow chart for calculating deflection influence line

2.1 基于计算机视觉的行人位置估计

2.1.1一般步骤

采用视觉方法估计行人位置可分为4个步骤，如图2所示。首先，对相机进行标定，校正由鱼眼镜头引起的径向畸变。然后利用添加遮挡模型改进的YOLOv3算法[24]检测行人并确定行人数目，给出被检测行人的识别结果，并将其作为跟踪目标。随后通过视觉跟踪算法来跟踪检测到的行人，将行人检测框中心点视为行人位置，并估计视频每一帧中的行人位置。最后，将图像坐标系中的行人位置转换到真实坐标系，实现对桥上行人位置的估计。

图2 行人位置估计一般步骤Fig.2 General steps of pedestrian position estimation

2.1.2相机标定

一个点从世界坐标系转换到像素坐标系的过程可以用式(5)表示[25]：

2.1.3行人检测

YOLOv3采用特征融合以及多尺度检测的方法，使得目标的检测精度和速度得到有效提升[24]，其可分为4个步骤。首先通过训练好的模型将图像划分为若干个单元格，预测候选框及其相对位置、置信度以及所属类别的后验概率P。然后映射变换预测的相对位置以及置信度，得到检测框。随后通过设定阈值T，如果检测框的置信度大于阈值T，则保留该检测框。最后对每个类别分别进行非极大值抑制处理，去除冗余窗口，输出留下的检测框的类别、位置、置信度。

在行人检测中，行人与结构、行人之间很容易出现遮挡情况，从而影响了行人检测系统的精度。行人周边相互遮挡的目标会影响预测框的位置，从而导致最终的预测框偏离真实目标，被环境部分遮挡的行人也很容易造成漏检情况的发生，最终导致行人检测系统性能的下降。为了能够准确预测在遮挡情况发生时预测框的位置，使用CityPersons训练集[27]中包含行人遮挡相互及被环境遮挡的2975张图片作为整个试验的训练集，按照7∶3的比例，使用自建的1275张图片作为整个试验的测试集。加入遮挡行人的数据集可以有效地提升存在遮挡情况的行人检测能力。图3为改进的YOLO算法在复杂环境下的行人检测结果。由图3可知经过改进的模型能够更容易检测出相互遮挡和被环境遮挡的行人。

图3 行人检测结果Fig.3 Pedestrian detection results

2.1.4 视觉跟踪

一旦在视频或图像序列的第一帧中检测到或选择了行人，就需要视觉跟踪来跟踪行人在连续图像中的位置。由于相机角度，即使相机静止，行人视图比例从开始到结束一直在变化。此外，由于行人之间以及行人与环境之间存在遮挡。所以视觉跟踪算法必须满足尺度不变性和视图鲁棒性的要求，并能在遮挡发生时预测目标位置。

本文使用卡尔曼滤波算法[28]实现行人目标跟踪，可以分为6个步骤，首先在YOLOv3检测到行人目标后，检查第一帧，获取矩形框的中心位置等信息。然后定义状态向量，根据前一帧的目标跟踪结果，利用卡尔曼滤波算法预测目标在当前帧的位置，将检测结果与预测结果进行最优相似度匹配。对于匹配成功的检测目标，用当前帧的预测及检测结果得到目标位置的最优估计值。最后显示跟踪结果并进行下一帧的预测。

2.1.5坐标变换

对图像中的行人位置(像素坐标)进行估计后，需要将其转换为真实世界坐标。在本研究中，假设桥面是一个平面，因此问题是将行人从图像平面转换为桥面平面。如图4所示，桥侧相机图像用于投影行人纵桥向位置，桥端相机图像用于投影行人横桥向位置。结合两台相机投影结果，真实世界对象(桥梁和行人)被投影到图像平面。最后，将行人的位置从图像坐标转换为现实世界的坐标，即桥面位置。在本文中，由于规定试验者以直线通过桥梁，则不需考虑横桥向位移，仅需一台相机即可确定人行所在桥面位置。

2.2 基于计算机视觉的结构位移测量

2.2.1一般步骤

基于视觉的方法从结构振动视频中测量位移一般分为4个步骤，如图5所示。首先对相机进行标定，计算出图像坐标系与真实坐标系间的几何转换关系。其次，从图像中选取测量目标作为图像子区域，提取子区域特征。第三，采用视觉跟踪算法结合选定的图像特征进行目标跟踪，并在视频每帧图像中更新目标区域的位置。最后，通过比较每帧图像中测量目标的位置变化，计算出图像坐标系中的位移，并结合相机标定结果和图像坐标系中的位移，得到实际坐标系中的最终位移。

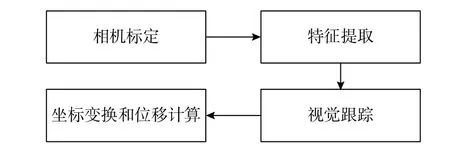
图5 视觉测量一般步骤Fig.5 General steps of visual measurement

2.2.2 视觉测量的相机标定实用方法

对于基于视觉的位移测量，相机标定与第2.1.2节中介绍的标定方法相同。但如果测量对象是无平面内运动或平面内运动可忽略的结构，即主要位移方向是为竖向，且使用的镜头是无畸变镜头时，可以采用一种更实用和简化的标度比法。当光轴垂直于位移方向时，比例因子s表示为式(7)[29]：

式中：D为选定对象的实际物理尺寸，单位为mm；d为该对象在图像中的像素尺寸，单位为像素。当目标运动平面与光轴之间存在角度时，比例因子必须通过以下来修正：

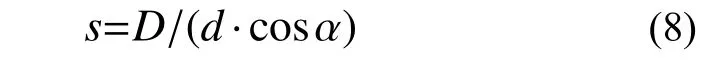
利用尺度比，可以很容易地将像素位移转换为真实位移。

2.2.3 LK 光流法目标跟踪

与行人跟踪不同，基于视觉的位移测量的跟踪目标更为简单，且视图比例变化不大。虽然位移测量目标的跟踪比行人跟踪要容易得多，但它需要更高的精度。一般来说，跟踪结果应该是亚像素级的。LK 光流法[30]运动目标跟踪的步骤为：首先在图像序列中利用Shi-Tomasi角点算法来检测当前帧的所有角点，然后利用这些角点作为特征点，计算当前帧的光流。通过对前一步骤算出的光流矢量进行阈值化处理，选择合理的阈值，除去超过阈值范围的所有光流矢量。最后生成各角点运动轨迹，并记录相应的位置坐标。图6为LK 光流法目标跟踪结果，圆点为检测到的角点位置，线条描述角点运动轨迹。

图6 LK 光流法目标跟踪结果Fig.6 Target tracking results of LK optical flow method

2.2.4位移计算与转换

检测当前帧中的特征点，将目标特征点作为跟踪点，其在图像中的像素坐标为(x1,y1)。通过灰度对比当前帧和下一帧，估计目标特征点在下一帧中的位置(x2,y2)，比例因子为s，则所选目标在竖直方向上的位移为s·(y2−y1)。

3 基于多项式分段拟合实测挠度影响线

影响线是结构在不同位置处受静态荷载作用引起的响应。然而在实际工程中，结构健康监测系统采集到的影响线是由桥上移动荷载引起的结构响应，不能忽略桥梁振动信息及其受行人动载效应的影响。且与静态荷载不同的是，行人本身是一个具有自适应能力的动力系统，结构发生振动或遇到障碍物时，行人会根据结构振动幅度大小以及障碍物形状及位置调节自身的步频、步长等来保持身体平衡，行人的本能调节过程会影响人行荷载的大小，进而影响结构响应。因此结合结构动力响应和行人参数的反演计算初始挠度影响线，对初始结果进行了多项式分段拟合，提取了具有准静态特性的桥梁位移变影响线，消除了桥梁振动干扰，提高影响线测试精度。从数值分析和现场试验的角度，验证了本文多项式分段拟合方法的准确度。对于简支梁，无损伤状态下桥梁跨中截面测点挠度影响线表达式为[31]：

式中：EI为桥梁抗弯刚度；Fp为单位荷载；x为荷载作用位置；L为桥梁计算跨度。可以看出，对于理想简支梁，挠度影响线由三次曲线分段函数表示。据此对实测试挠度影响线采用三次多项式进行拟合可得到更加准确的准静态影响线。

4 试验验证

4.1 试验步骤

试验在单跨简支人行桥模型上得到了验证。该桥是中型实际结构的缩小模型，桥面总质量1580 kg，桥面长10 m、宽1.6 m，计算跨度为9.8 m。

为避免测试者因不规范行走姿势造成的不可靠数据，本试验将两个维特智能BWT61CL 无线传感器分别固定在每个测试者质心位置前后，取两无线传感器获得的连续荷载时程平均值作为一次试验数据。每位测试者被要求穿着硬质鞋底的运动鞋，在人行桥上以慢速1.05 Hz、中速1.6 Hz、快速2.1 Hz 的固定步频行走完成3次步行试验。

为了跟踪行人通过桥面的整个过程，在距桥跨中4 m 处的三脚架上安装了一台带有鱼眼广角镜头的大疆灵眸Action 运动相机。相机可与智能手机连接，进行远程非接触控制，避免了由于接触操控使得相机抖动而造成的误差。设置视频分辨率为4K(3840像素×2160像素)，帧数为50 fps。使用鱼眼广角镜头可为相机提供了一个大角度，以确保整个桥梁在相机拍摄视野中。如图7所示，鱼眼镜头拍摄的图像存在严重的径向畸变，且图像中的直线桥变为曲线桥，故必须对相机进行校正。校正后图像如图8所示。

图7 带畸变图像Fig.7 Image with distortion

图8 畸变校准后图像Fig.8 Distortion correction image

将一台佳能5D4相机安装在桥梁跨中1.5 m 处的三脚架上，用于测量桥梁位移。选用加装24 mm～105 mm 变焦镜头的佳能相机，相机可通过佳能官方应用程序与智能手机连接，设置视频分辨率为1080P(1920像素×1080像素)，帧数为50 fps。同时在桥下安装一个激光位移计，以验证视觉测量的准确性，激光位移计型号为Banner 250U，采样频率为200 Hz。试验过程中，行人从桥的一侧移动到另一侧，相机和激光位移计同步记录桥梁跨中位移。

现场试验情况如图9所示。在试验开始时测试者发出“开始”的指令随即开始行走并通过桥梁，在结束时发出“停止”指令随即停止行走。在此过程中，两台相机在分别从始至终记录行人、结构行为的同时记录外界音频信号。通过对比两台相机记录的音频信号中起止指令所在时刻截取视频片断并同步相机。

图9 现场试验情况Fig.9 Test scenario

4.2 视觉测量精度检验

图10为行人步频为2.15 Hz 时桥梁跨中处位移对比，其中实线、虚线分别为视觉测量法与激光位移计测得的桥梁跨中处位移。图10表明两种方法获得的位移结果非常一致。其归一化互相关(NCC)为99.95%。图11为行人步频为2.15 Hz 时桥梁跨中处位移傅里叶幅值对比，其中视觉测量法前两阶DLF相较于激光位移计的误差分别为3.2%、3.3%。结合图10和图11可知，本文使用的视觉测量方法可准确测量桥梁位移。

图10 步频2.15 Hz 时的位移对比Fig.10 Displacement comparison of 2.15 Hz step frequency

图11 步频2.15 Hz 时的傅里叶幅值对比Fig.11 Fourier amplitudecomparison of 2.15 Hz step frequency

4.3 试验分析与结果

由于篇幅限制，取体重为636 N的测试者以1.6 Hz 步频通过人行桥的工况分析，通过无线传感器测得行人竖向加速度时程，经傅里叶变换后通过式(3)计算人行荷载(取前4阶DLF及相位角)。图12为重量为636 N 的测试者在步频为1.6 Hz时的竖向加速度时程曲线(消除重力加速度g)。图13为对应的人行荷载时程曲线。图14为通过目标跟踪估计得到的行人位置信息，其中实线为初始行人位置，虚线为拟合后的行人位置。由图14可知，初始行人位置存在明显的倒退行走，显然这与实际情况不符，行人是匀速通过桥梁的，故需对初始行人位置进行线性拟合，a表示时间，b表示行人位置。通过视觉测量得到的结构位移响应，如图15所示。

图12 步频1.6 Hz 时的竖向加速度时程Fig.12 Vertical acceleration timehistory of 1.6 Hz step frequency

图13 步频1.6 Hz 时的人行荷载时程Fig.13 Pedestrian load time history of 1.6 Hz step frequency

图14 步频1.6 Hz 时的行人位置Fig.14 Pedestrian position of 1.6 Hz step frequency

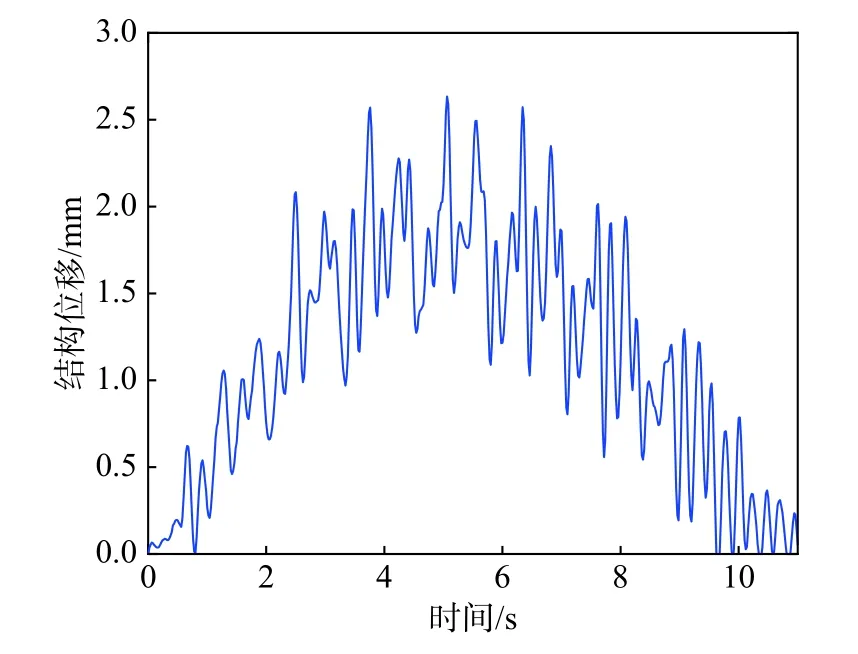
图15 步频1.6 Hz 时的结构位移Fig.15 Structural displacement of 1.6 Hz step frequency

通过无线传感器得到的人行荷载时程，结合视觉测量方法得到的位移响应和跟踪估计的行人位置信息，建立了实测挠度影响线，如图16所示，实线表示实测挠度影响线，划线表示采用多项式分段拟合得到的挠度影响线。由图16可知，反算得到的实测挠度影响线包含桥梁振动信息，且随着行人步频变快越显著；对实测影响线进行分段拟合后，拟合值与理论值接近，能较好地消除桥梁振动以及人行动载效应的影响，适用于行人步频快、桥面平顺性差的工况。图17为桥梁挠度影响线拟合值与理论值对比。由图17可知，两影响线基本吻合，峰值位置存在误差，这是由于计算人行荷载时假定步行过程是周期性的，而实际行人的步行过程接近于一个窄带的随机过程[32]，很难保证完美的周期性。并且计算挠度影响线理论值时假定桥梁两端是简支的，而实际桥梁并不完全简支。挠度影响线理论值的峰值出现在桥梁计算跨度跨中4.9 m 位置处，峰值为4.137。挠度影响线拟合值的峰值出现在4.48 m 位置处，较理论值误差为8.57%，峰值为4.131，较理论值误差为0.15%。

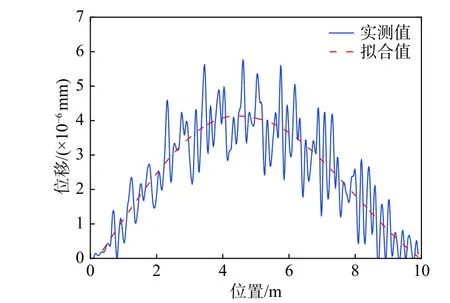
图16 挠度影响线拟合Fig.16 Fitting of deflection influence lines

图17 挠度影响线对比Fig.17 Comparison of deflection influence lines

5 结论

为了克服传统的结构健康监测方法成本高、安装时间过长、需要大量劳动力从事电缆布线工作等不便和缺点，建立了一个完全非接触式影响线识别系统中。桥梁挠度影响线通过便携式相机、计算机视觉和无线传感器识别。通过一系列室内试验对比研究，验证了该方法的可行性。主要的研究方法、发现和结论如下：

(1)提出了一种基于视觉的结构输入(行人位置)估计方法。通过添加遮挡模型改进YOLOv3算法，在行人检测过程中，即使在发生遮挡的情况下，也能成功地检测跟踪到行人。

(2)为了扩大摄像机的视野，并在整个过程中跟踪行人，采用广角鱼眼相机，对相机标定，校准径向畸变，实现精确的行人位置估计。

(3)利用LK 光流法进行目标跟踪测量位移测量，得到的位移响应与激光位移计的结果具有很高的一致性，NCC 系数为99.95%。

(4)将视觉跟踪估计行人位置、视觉测量得到的位移响应相结合与无线传感器得到的行人加速度时程相结合，成功地识别出了实测挠度影响线，并通过多项式分段拟合得到与理论值接近的拟合挠度影响线，影响线峰值误差为0.15%，峰值位置误差为8.57%。