软土地区交通荷载下几种长期沉降模型的分析比较

赵 宏 王 菊 杨富莲

（皖西学院建筑与土木工程学院，安徽六安 237012）

现有的铁路路基长期沉降规律计算模型主要有两类。基于复杂的动力本构模型如边界面模型和多屈服面模型，这类模型需要经过循环荷载的往返重复计算，计算量较大。经验参数的拟合模型，经验模型由于计算量较小，参数获得较容易，经验参数应用广泛。

常用的有以Monismith等[1-2]为代表的指数模型，以王元战[3]为代表的双曲线模型，以Parr[4]、庄海洋[5]、Sakai[6]为代表的对数模型。土体在交通荷载作用下长期沉降模型除与土体的动偏应力、静偏应力、循环荷载等影响因素外，还与土体的固结状态（超固结土的固结比）以及结构性土有关。刘新峰[7]研究不同OCR（超固结比）状态下的土体的累积塑性变形随循环变化的规律，将此规律应用于飞机跑道下土体的累积沉降，预测温州机场的长期沉降。杨洋[8]利用空心圆柱实验研究OCR对累积应变、孔压的规律的研究，提出预测相应的累积应变方程。

臧濛[9]采用特殊的取土器用动三轴试验获得结构性土体的力学参数，研究土体在动荷载下的累积变形，发现土体在循环高动偏应力比的情况下会出现破坏型的累积塑性变形，在低动偏应力比的情况下出现稳定型累积变形。刘维正[10]、瞿帅[11]采用人工措施模拟颗粒间的胶结，研究循环荷载下塑性累积变形随荷载次数的关系，提出三种塑性累积变形预测模型。

1 计算模型

1.1 指数模型的选取

本文采用的指数模型是用途较广的是以Monismith为代表的指数模型，本文采用较有代表性的LI模型[2]：

式中：εp——残余变形；qd——动偏应力；qf——静强度；N——荷载作用次数；a，m，b——参数。

1.2 对数模型的选取

Behzad[12]给出残余变形与循环荷载间是对数函数关系：

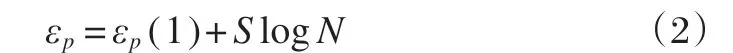
可以简化为：

1.3 双曲线函数模型

2 选取计算土体模型

2.1 普通软黏土模型（天津软土）

本文选择刘维正[10]模型中的数据，土体沉降模型的土体取自天津软土的动三轴试验的试验数据。

指数预测模型的精度较高，在循环应力比较大的时候，精度较小，采缺点是当循环次数趋于无穷大时，累积变形趋于无穷，合理性较差。

指数、对数、双曲线模型如图1～图3所示。

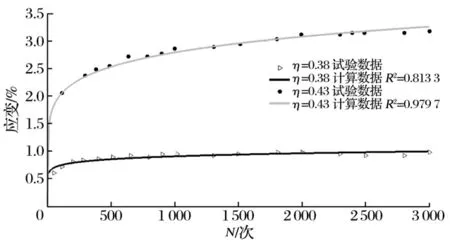
图1 软土累积应变（指数模型）

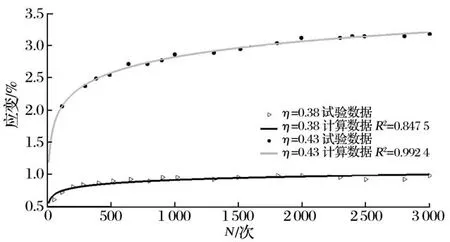
图2 软土累积应变（对数模型）

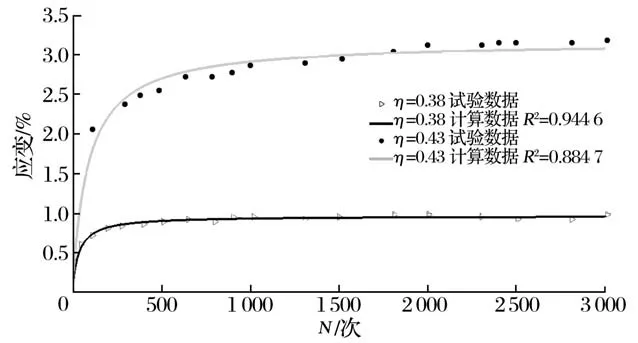
图3 软土累积应变（双曲线模型）

2.2 超固结软土模型

土是漫长的地质年代形成的产物，岩石与大气、水等环境相互作用，使原本地表的土体被剥蚀，下层的土体形成超固结状态。超固结土的土体应力状态处于超固结状态。即超固结比OCR>1，从受力的角度分析，有利于地基的变形控制，承载力提高，超固结土循环应力的路径不同，使长期沉降变形的规律更复杂。本文选取刘新峰[7]的试验数据进行研究。

指数、对数、双曲线模型计算数据如图4～图5所示。

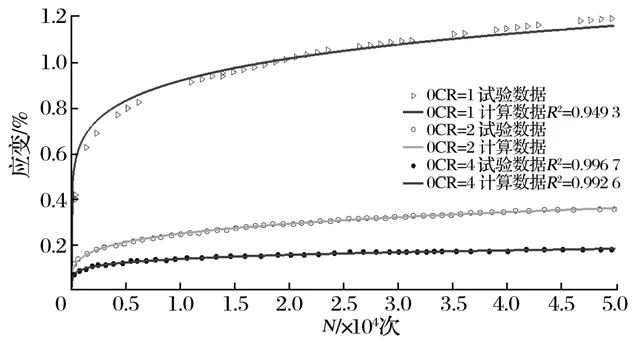
图4 采用指数函数模型计算的数据

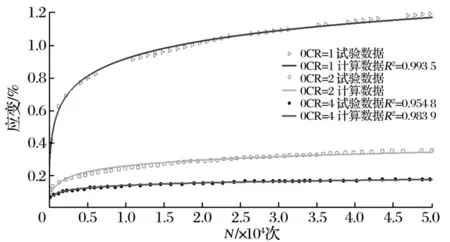
图5 采用对数函数模型计算的数据

图6 采用双曲线模型计算的数据

采用指数模型和对数模型可以获得较好的计算结果，拟合精度较高，正常固结土采用对数模型比指数模型可以获得更好的计算结果。对于超固结土，土体的再压缩指数小于土体的压缩指数，土体的累积循环应变很快就进入稳定期，对于超固结土的循环荷载作用下土体的累积应变采用对数模型、指数模型、双曲线模型都可以获得较好的效果，采用双曲线模型时候，固结比越大，计算结果越精确。整体而言，对数模型优于指数模型，优于双曲线模型。

2.3 结构软土模型

对于实际的土体在原位状态下承受荷载，我国广大南方地区铁路路基都分布在软土地基上，软土结构的破坏模型分为破坏型、稳定型。稳定型累积曲线模型适用普通的软土，较多土体长期沉降集中呈现增长型破坏类型。本文的计算数据采用的是瞿帅[11]的模型数据。

三种模型计算数据如图7～图9所示。

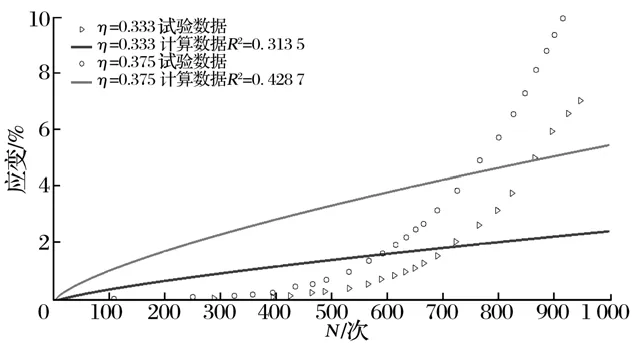
图7 采用指数函数模型计算的数据

图8 采用对数函数模型计算的数据

图9 采用双曲线模型计算的数据

指数模型反映的是累计塑性应变随循环荷载次数的增加越来越平缓，累积的塑性应变越来越小，指数模型描述这类土体时误差较大。对数模型在描述破坏型模式土体的累积塑性应变时误差较大，但比指数函数误差小。双曲线模型反映破坏型模式土体的累积塑性应变时误差较小，双曲线模型优于对数和指数模型。

3 结语

三种模型在普通软黏土即累积塑性变形随荷载作用次数趋于稳定情况下，可预测长期沉降，长期沉降模型效果预测较好。超固结土在超固结比小的情况下，指数模型和对数模型优于双曲线模型，较大的情况下三种模型都可以获得较好的计算结果，精度较高结构性软土。在高动应力比的情况下出现破坏式累积塑性变形，双曲线模型计算精度优于指数函数模型和对数模型。