一种高增益升压Cuk变换器及其改进模糊控制
林维明,曾涛,陈红星
(福州大学 福建省新能源发电与电能变换重点实验室,福州 350108)
0 引 言
随着环境污染问题日益严重,太阳能,风能等新能源的开发及利用受到极大的关注。通常太阳能电池输出电压较低(20~50 V),需采用具有高增益特性的DC-DC变换器升压[1-3]。此外在许多工业应用场合中,如航空电源、电动汽车能源系统、不间断电源(uninterruptible power supply,UPS)等应用中,高增益DC-DC变换器也起着重要作用[4-5]。
文献[6]将倍压整流电路引入反激电路,在开关管导通关断期间均有能量传至副边,提高了变压器的利用率,并通过增加变压器副边倍压单元以减小匝比并实现高压输出。然而其只适用于小功率场合。文献[7]将二极管电容单元引入传统二次型Boost变换器[8],解决了二次型Boost电路器件电压应力高的问题,然而二极管电容的引入使得电路器件进一步增多。文献[9]将开关器件与电感组成的升压单元,即开关电感单元,与二极管电容单元引入Cuk电路以提高电路增益,然而开关电感的引入使电路磁性器件较多而不利于减小电路体积,且开关为有源开关,加大了控制难度。文献[10]在耦合电感型Boost电路中引入LCD无损吸收电路,解决了漏感引起的电压尖峰问题。然而在开关管开通时,该吸收电路的谐振使开关管电流存在较大振荡,这将加重电路产生的电磁干扰(electromagnetic interference,EMI)。另外,在中大功率应用场合,低压侧半导体器件电流应力往往较大,文献[11-12]采用交错并联的方式以减小器件的电流应力并减小了输入侧电流纹波,然而均存在器件数目多,效率偏低的问题。
由于高增益应用场合变换器输入往往是波动较大的低压直流电,且输出侧负载变化范围较大,因此提高变换器的抗干扰能力十分重要。由于具有升压功能的拓扑及其衍生拓扑从占空比到输出电压传递函数中存在右半平面零点[13-16],变换器动态性能和稳定性受到一定影响,采用PID控制在扰动剧烈情况下难以保证变换器的动态性能。模糊控制作为一种非线性智能控制策略,具有无需被控对象的精确模型,鲁棒性强等特点,因而较多文献对其在DC-DC变换器中的应用做了研究[17-23]。文献[17]对比了PID与模糊PID控制在Boost电路启动过程以及切载过程的控制效果,表明模糊PID控制对动态响应速度有一定的改善,并对稳态工作点的变化具有较好地适应能力。文献[18] 将模糊PID控制作为电压外环而内环采用平均电流控制,限制了启动时电感电流,且较单环控制相比,在输入电压及负载扰动时具有更好的抗扰性能;文献[19]将变论域模糊PID控制用于Boost变换器,通过动态改变模糊控制器输入输出论域提高模糊PID在小误差下的控制精度;文献[20]采用滑模控制与模糊控制相结合的方式,减小了滑模控制固有的抖振问题。文献[21]以负载电流为基准,并以基准电流与电感电流的差值及其变化率作为模糊控制器的输入,提高了负载的抗扰能力,然而其需要采样负载电流、电感电流,输出电压等参量进行运算,加大了控制复杂性。通常一型模糊控制器基于专家经验设计,其模糊规则和隶属函数形状等选取存在不确定性,为了解决这一问题,文献[22]采用二型模糊控制,然而与一型模糊控制相比,二型模糊控制需要进行降阶处理,增大了计算负担。文献[23]基于Takagi-Sugeno-Kang (TSK)模糊双线性模型提出一种模糊双线性状态反馈控制策略,实现变换器闭环全局稳定,然而这种控制设计复杂,不利于实现。
本文基于升压Cuk变换器[24]提出一种高增益升压Cuk变换器,利用二极管电容单元对漏感能量进行吸收,减小开关管电压应力,并提高升压增益;为了提高变换器动态性能,本文提出一种改进模糊控制策略,其具有规则数少,控制简化等优点;通过动态改变控制器比例因子,变换器具有快速的动态响应速度。文中对提出电路及控制策略进行详细分析并设计一台输入为36~70 V,额定输出400 V/400 W的样机,实验结果表明变换器增益得到有效提高,开关管电压尖峰得到抑制;提出的改进模糊控制策略能更有效地抑制扰动。
1 一种高增益升压Cuk电路
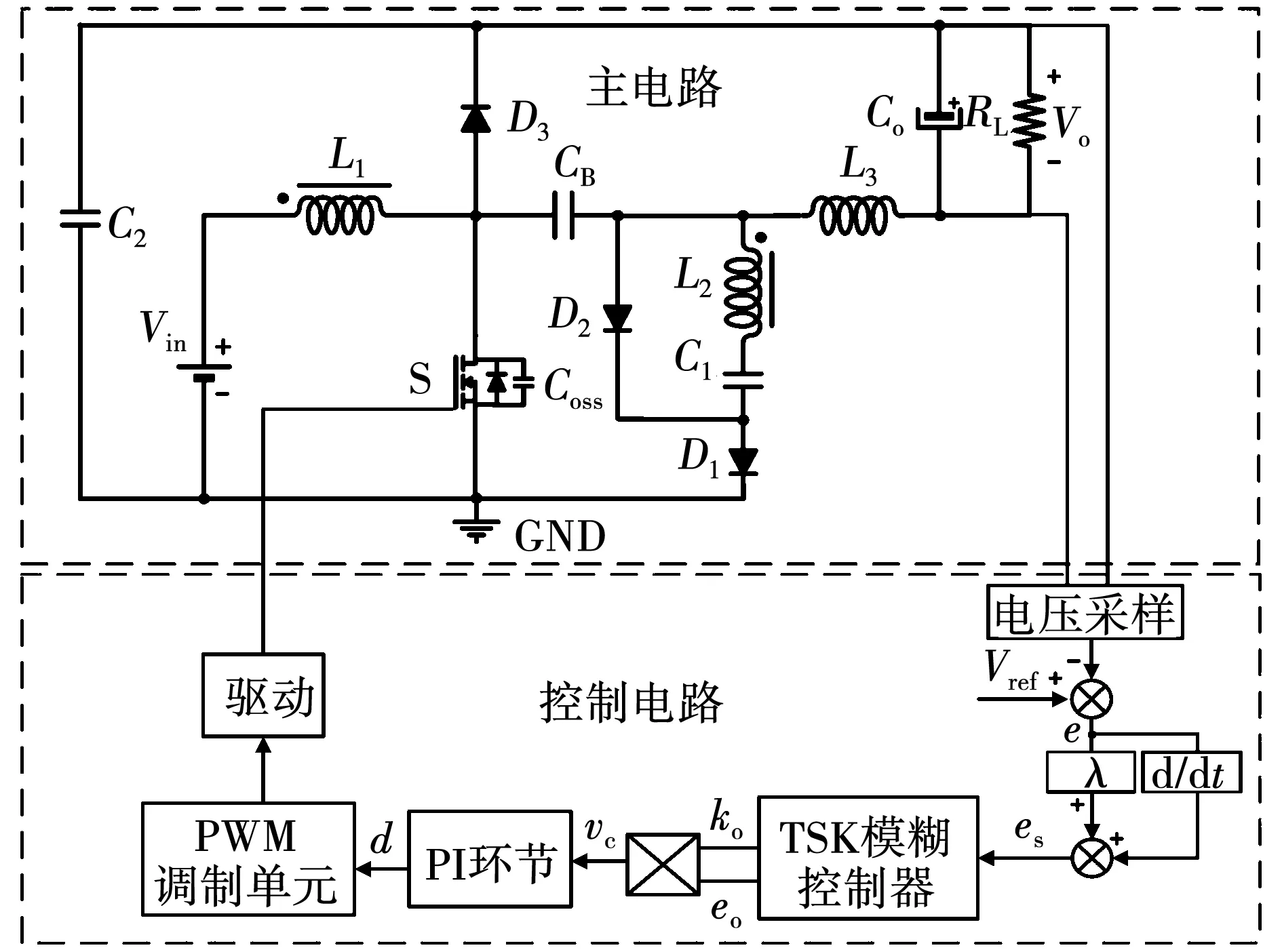
1.1 电路结构
图1为本文提出的一种高增益升压Cuk电路。电路结构如图1(a)所示,通过将耦合电感等效为非理想变压器模型,并将漏感折算至绕组1侧,得到对应等效电路如图1(b)所示。
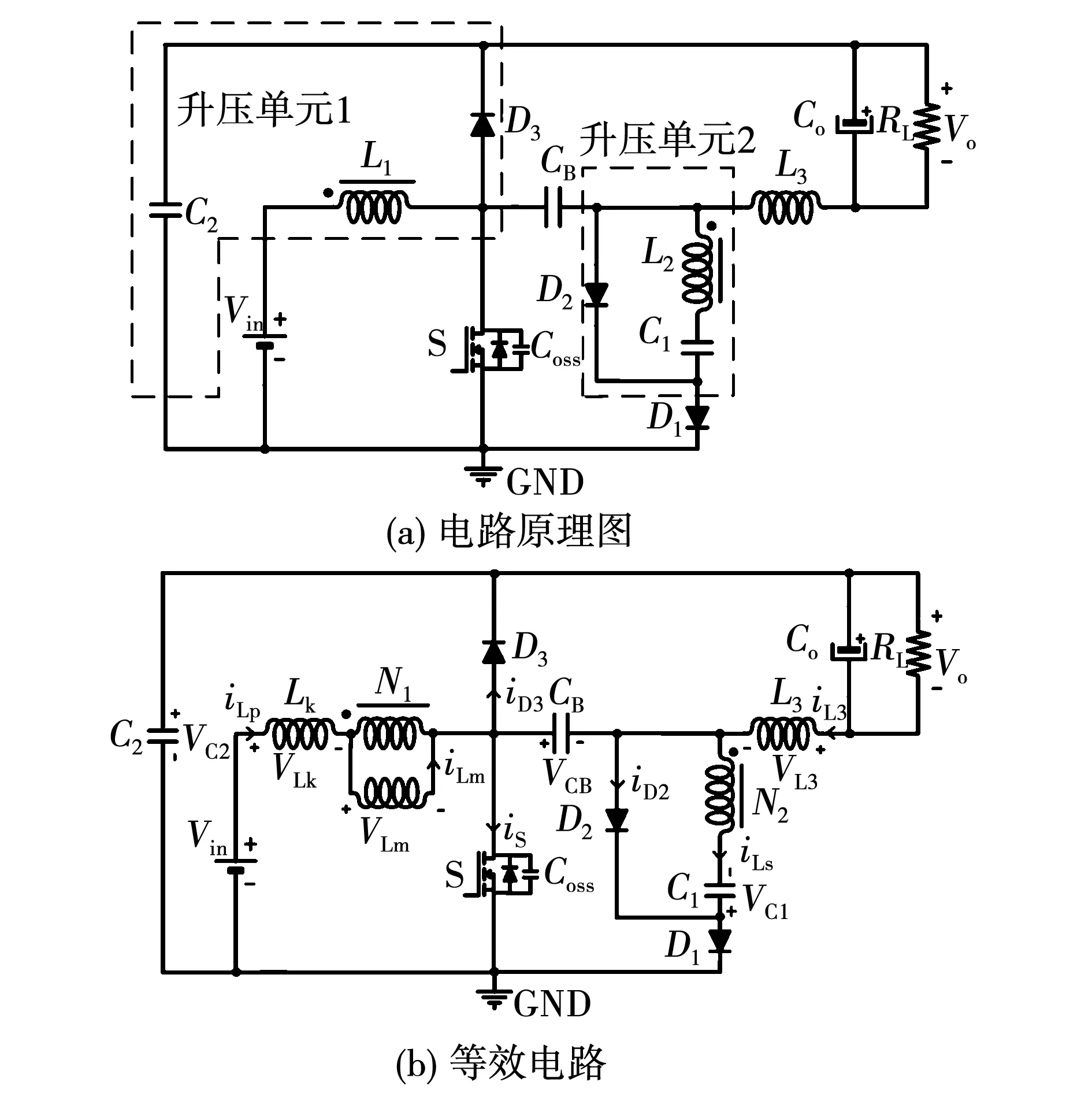
图1 一种高增益升压Cuk电路Fig.1 A high gain step-up Cuk converter
其中:L1、L2组成耦合电感;L3为输出侧电感;N1、N2分别为耦合电感两绕组1、2的匝数,且有N2/N1=N、Lk为等效至绕组1的漏感,k为漏感系数,且有Lk=kLm;二极管D2、D3分别与电容C1,C2构成两个二极管电容升压单元。
1.2 工作原理
为了简化分析,假设:1)除考虑开关管寄生电容外,各半导体器件为理想器件;2)各电容两端电压纹波稳态时较小,分析时可用其平均值代替,即vCB≈VCB,vC1≈VC1,vC2≈VC2。
电路在CCM模式下稳态工作时共有5个模态,各模态等效电路如图2所示,各关键参量开关周期波形图如图3所示。稳态时,电路在一个开关周期中的工作过程分析如下:
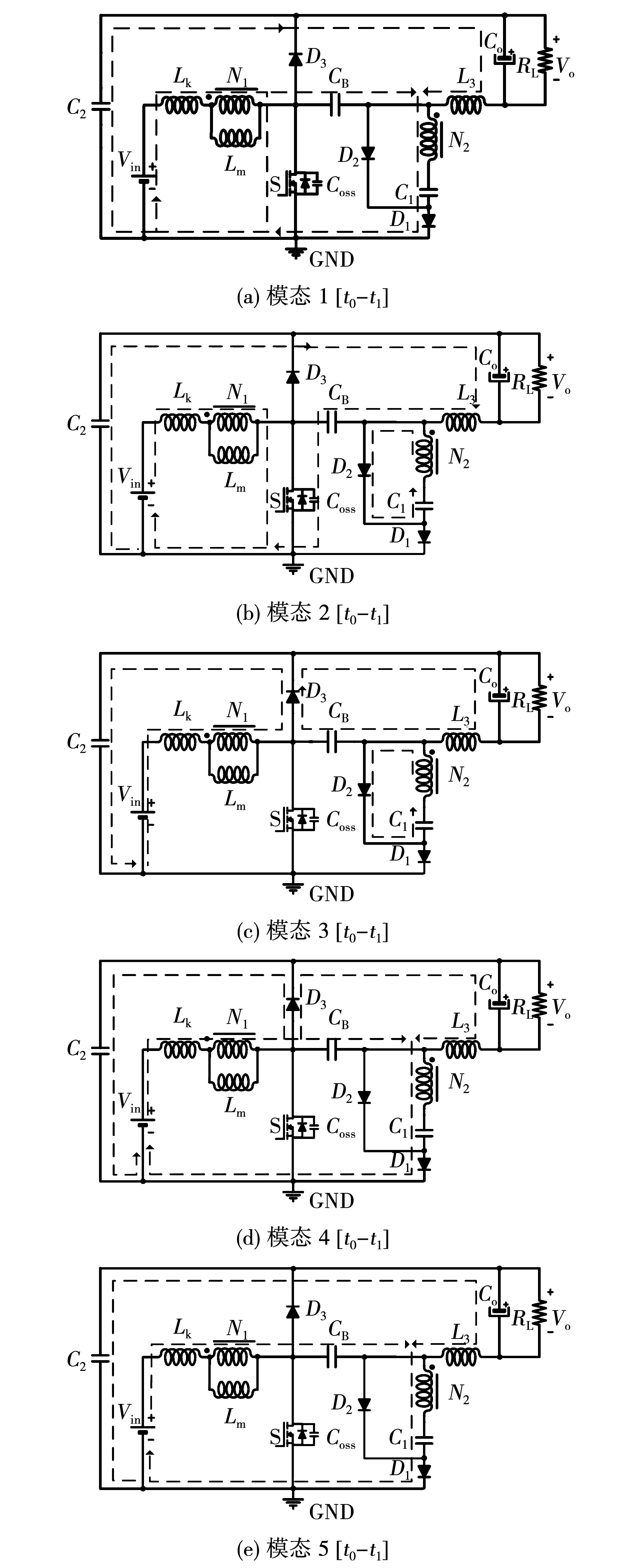
图2 各模态等效电路Fig.2 Equivalent circuit of the operation modes
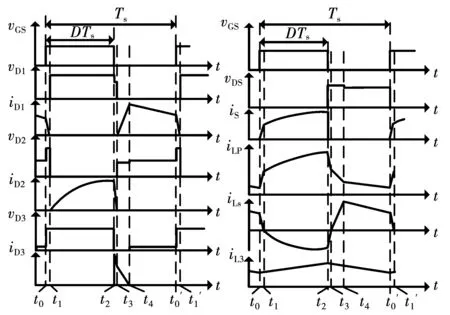
图3 关键器件波形Fig.3 Main operation waveforms of key components
模态1[t0-t1]:t0时刻,开关管S开通,此时二极管D1仍处于导通状态。由磁动势平衡式可得该模态二极管D1电流iD1表达式为
(1)
由式(1)可知,二极管D1电流iD1为漏感电流与励磁电感电流的线性组合,故iD1以一定斜率逐渐减小至零,实现ZCS关断,减小了二极管D1反向恢复问题。该模态开关管S电流表达式为
iS(t)=iLp(t)-iLs(t)+iL3(t)=
(2)
由于式(2)中iS为漏感电流、输出侧电感电流和励磁电流的线性组合,且在t0时刻前,式子右边等于0,因此开关管S电流从零开始上升。该模态励磁电感电压和电流分别为:
(3)
(4)
该模态二极管D2两端电压为VCB,二极管D3两端电压为VC2。直到t1时刻,二极管D1关断,该模态结束。
模态2[t1-t2]:t1时刻二极管D1关断,二极管D2开通,绕组2通过二极管D2向电容C1充电,C1折算到绕组1并联励磁电感Lm与绕组1的漏感Lk谐振,由于开关频率下励磁电感阻抗远大于电容阻抗,若不考虑励磁电感支路,则有:
(5)
(6)
若谐振周期远大于开关周期,则该模态耦合电感绕组1、2电流的变化率可近似为恒定值。由式(6)可知电容C1平均电压为
VC1=NVin。
(7)
考虑漏感分压,该模态励磁电感电压、电流有:
(8)
(9)
而输出侧电感电流和开关管电流分别为:
(10)
iS(t)=iLm(t)+NiC1(t)+iL3(t)。
(11)
该模态中二极管D1承受的电压为VCB,二极管D3承受的电压为VC2。t2时刻,开关管S关断,进入下一模态。
模态3[t2-t3]:t2时刻开关管S关断,漏感与开关管S输出电容Coss谐振产生开关管电压尖峰使得二极管D3导通,漏感能量通过二极管D3向电容C2释放,S电压被钳位至VC2。由于二极管D2仍然导通,因此励磁电感电压仍近似为Vin,iLm继续上升,若忽略C2电压纹波,则绕组1电流iLp表达式为
(12)
绕组1电流线性下降,由于该模态时间很短,iL3近似不变,故流过二极管D3和D2的电流分别为:
iD3(t)≈iLp(t)+iL3(t2);
(13)
(14)
因此iD2也线性下降,该模态二极管D1电压为VCB-VC2。t3时刻,iLp=iLm,二极管D2电流iD2线性下降至0,实现ZCS关断,此后iLs反向,二极管D1导通,进入下一模态。
模态4[t3-t4]:t3时刻二极管D1导通,二极管D2承受电压为VCB-VC2,二极管D3仍导通,绕组1励磁电感电压反向,输入电压加上绕组1上电压通过二极管D3向电容C2充电,导致电容C2电压vC2不断上升,同时输出侧电感电流iL3也通过二极管D3流向负载。由于漏感分压作用,该模态绕组1电流iLp近似有
(15)
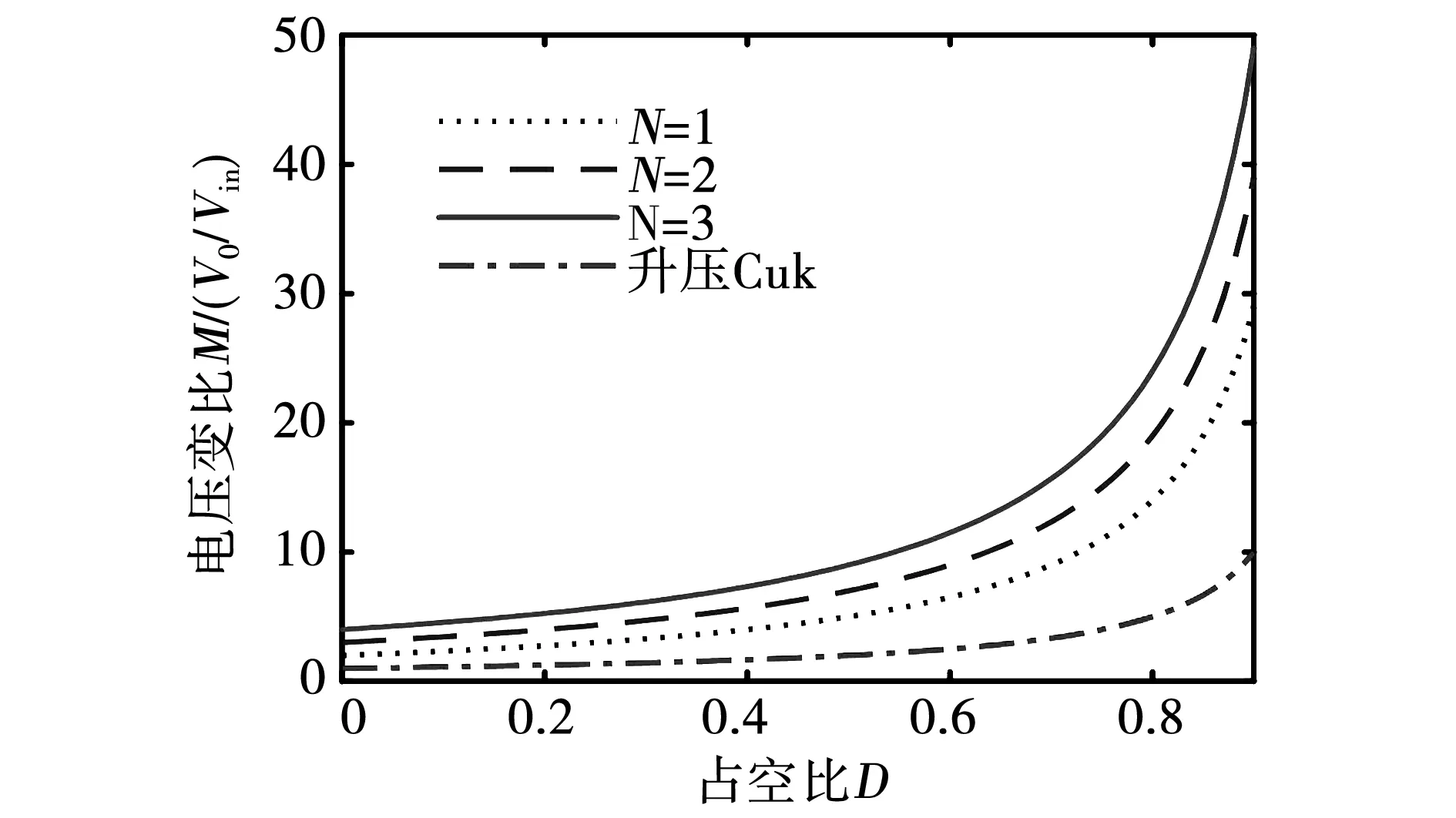
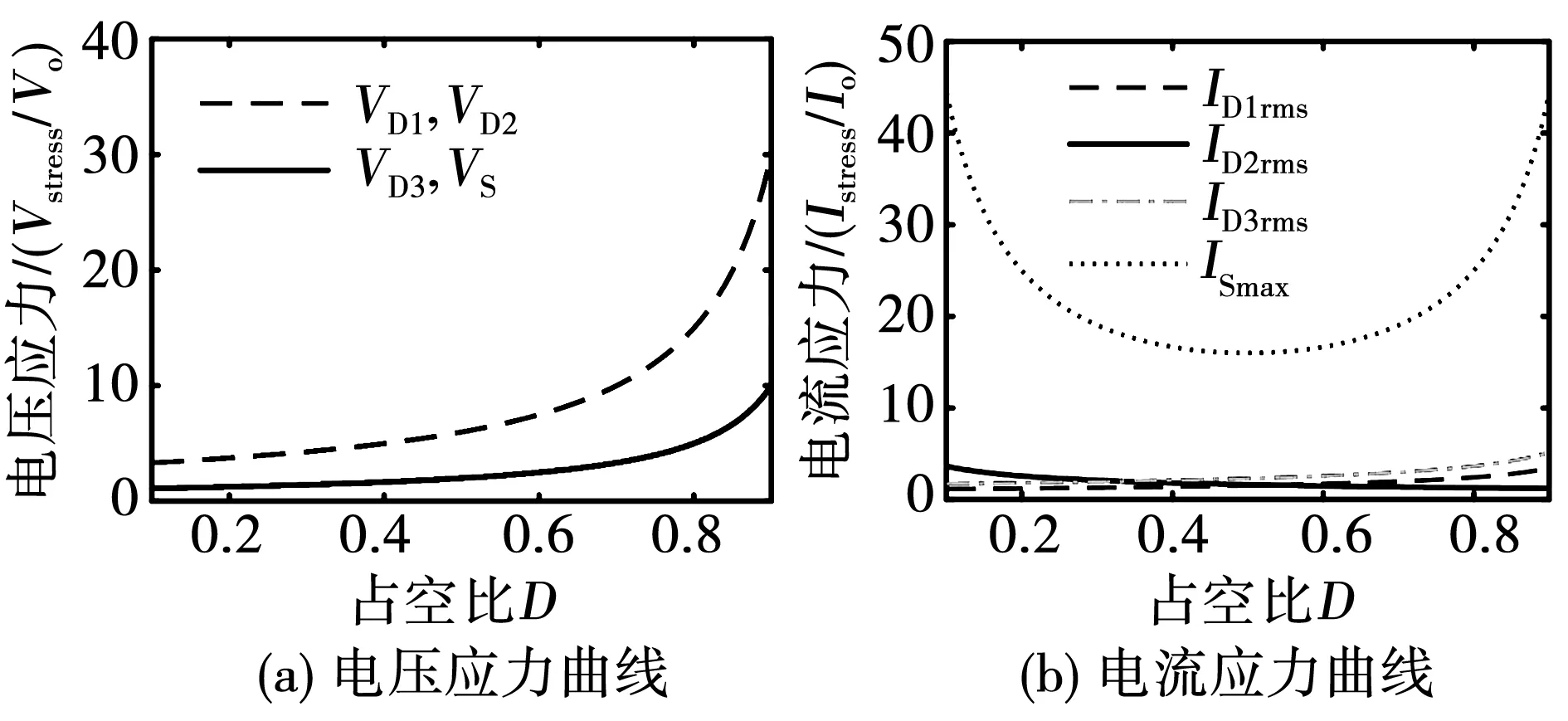
iLp不断减小,并有iLp (16) 该模态开关管S两端电压仍然为VC2,二极管D2两端电压为 vD2=VCB-VC2。 (17) 该模态下励磁电感Lm电压、电流分别为: (18) (19) 而输出侧电感L3电流为 (20) 由Vin、CB、C1及绕组1、2构成回路可得 (21) 因此有 vLm4=vLm5。 (22) 由式(16)可知,二极管D3电流不能突变。随着C2电压的不断增加,iD3逐渐减小,直到t4时刻,二极管D3实现ZCS关断,此模态结束。 模态5[t4-t0']:t4时刻,二极管D3关断,二极管D1仍处于导通状态。该模态励磁电感电压如式(21)所示,二极管D3承受的电压为 vD3(t)=vC2(t)+vLm5(t)+vLk(t)-Vin。 (23) 该模态中流过二极管D1的电流为 (24) 此外,iLm、iL3均线性减小,故iD1线性减小。该模态开关管S承受电压仍然约为VC2,二极管D2承受电压与式(17)近似相等。直到开关管S开通,进入下一个开关周期。 1.3.1 变比关系分析 如上节分析,模态1,3时间较短,若忽略这两个模态,且不考虑电容电压纹波,由式(8)、式(21)、式(22)对励磁电感列写伏秒平衡式可得 (25) 由于稳态时各电感电压开关周期平均值为0,故中间电容CB上的平均电压为 VCB=Vin+Vo-VC2。 (26) 由式(7)、式(18)、式(21)、式(22)、式(25)与式(26),可得变换器在CCM条件下的变比为 (27) 而通常k<<1,故可忽略漏感作用,即 (28) 图4给出了不同匝比下变比M随占空比D变化的关系曲线。 图4 不同匝比下的变换器增益曲线Fig.4 Gain curve of the proposed converter under different turns ratio 由图4可见,所提出变换器有效地提高了升压Cuk变换器的电压增益,且通过增加匝比可进一步提高电压增益。 1.3.2 功率器件电压应力分析 如1.3.1小节分析,由式(7)、式(18)、式(21)、式(22)、式(25)与式(26)可得到各二极管电压应力为: (29) (30) 以及开关管S电压应力为 (31) 可见各二极管电压应力均小于输出电压。而在考虑漏感和不考虑漏感条件下,由于D3都会导通,式(31)均成立,因此有效地抑制了开关管电压应力。故提出电路在获得高电压增益特性的同时还具备低开关管电压应力的优点。 1.3.3 功率器件电流应力分析 (32) 由于二极管D2导通时间为t2-t1≈DTs,且二极管D2在导通时电流近似线性上升,因此可求得二极管D2电流应力为 (33) 在模态4初始时刻t3有iLm=iLp,因此可得 (34) 由于iD3在模态4近似线性下降,因此可求出模态4持续的时间近似为 (35) 因此,二极管D3电流应力为 (36) 开关管S导通时间为DTs,且模态2中流过开关管的电流为 iS=iLm+NiD2+iL3。 (37) 故开关管S电流应力为 (38) 图5分别给出了匝比N=2时各功率体器件电压应力与电流应力随占空比变化的曲线。 图5 功率器件电压电流应力曲线Fig.5 Voltage stress curve of power devices 从图5可知,开关管与各二极管电压应力均随占空比增加而增加。当占空比过大或过小时,开关管电流应力都较大,二极管D1,D3电流应力随占空比的增大而增大,而二极管D2电流应力随占空比增大而减小。 1.4.1 匝比设计 由变比表达式(28)可知 (39) 从图5的分析可知,过大和过小的占空比均将导致电路中某些半导体器件电压应力或电流应力的较大程度增加,因此可先选择一个合适的占空比大小(如0.3~0.7),再来确定匝比大小。 1.4.2 电感设计 取N=2,输入电压范围为36~70 V,因此Dmin=0.40,Dmax=0.67,为了保证变换器工作在CCM模式下,则需保证 (40) 其中:τLe=Lefs/RL;Le=Lm/L3。 而输出侧电感L3的选取,可根据规定的电感电流峰峰值允许大小决定,即 (41) 其中β=ΔIL3/IL3。再由式(40)可以确定保证变换器工作在CCM情况下Lm需满足的条件: Lm> (42) 其中RLmax为保证满足CCM条件下的最大负载电阻。 1.4.3 电容设计 在开关管S开通期间,中间电容CB放电,电流为-iL3,故电容在一个开关周期电压变化量为 (43) 与此同时,绕组2通过二极管D2给C1充电,故电容C1电压变化量为 (44) 在模态4中,二极管D3导通,可求得C2电压变化量为 (45) 若假定电流iL3的交流纹波分量完全流入输出电容Co,则可求得输出电变化量为 (46) 故可根据电压纹波允许量,由下式选取容值: (47) 其中RLn为额定负载电阻。 本文提出一种变输出比例因子的模糊控制策略,该控制策略主要由输出电压采样环节、TSK模糊控制器、PI环节构成,其中TSK模糊控制器为0阶模糊控制器,构成的闭环系统结构如图6所示。 图6 改进模糊控制策略原理图Fig.6 Improved fuzzy control schematic 如图6所示,该控制策略通过采集输出电压与基准进行比较,得到电压误差e,经过运算得到模糊控制器输入的误差函数为 es=CTE。 (48) 其中:C=[λ,1]T;E=[e,de/dt]T。该误差函数送入TSK模糊控制器,产生两个输出ko、eo,并相乘得到控制电压vc,再通过PI环节后产生对应占空比来控制变换器。通过调节TSK模糊控制器的输出使es=0,有 (49) 则误差将呈指数规律收敛至0。其中λ决定了误差的收敛速度。 模糊控制器输出误差eo与比例因子ko相乘产生控制量vc。对于比例因子选取而言,若取值较小,则遇到大扰动,变换器动态调节时间变长,动态性能变差。若取值较大,虽然对大扰动有更快的反应,但会导致控制器在小误差下仍有较大输出,使变换器输出电压产生低频振荡。通过模糊控制器动态调整比例因子的大小来提高系统的动态性能。 采用0阶TSK模糊控制器[25]以简化计算,模糊规则采用如下规则形式 Ri:ifesis NB theneoisyiandkoiszi。 (50) 模糊规则后件中的eo、ko均为7个模糊单值,模糊规则库共7条模糊规则,如表1所示。 表1 模糊规则表Table 1 Fuzzy rule table 通过解模糊运算得到的输入es与输出误差eo的关系式为 (51) 输入模糊集合隶属函数分布以及输入误差es与输出误差eo的关系曲线如图7所示。 图7 隶属函数分布与输出误差变化曲线Fig.7 Membership functions distribution and output error variation curve 通过解模糊运算得到的输入误差es与输出ko之间的关系式为 (52) 控制器输入误差es与输出比例因子ko关系曲线以及输入误差es与控制量vc关系曲线如图8所示。 图8 比例因子变化曲线Fig.8 Curves of scale factor and vc variation 由上图可见,当es在0附近时,vc变化曲线较为平缓,而在大误差下其更为陡峭,饱和输出由-1,1拓展到了-2和2。 最后,输出占空比随控制量vc的变化关系为 (53) 对所提电路进行了仿真,工作条件为输入48 V,输出400 V/400 W,电路器件参数与实验基本一致。 变换器工作在CCM模式下,稳态工作时,关键器件开关周期电压电流仿真波形如图9所示。 图9 关键器件稳态波形Fig.9 Stable waveforms of key components 为验证所提出控制策略的有效性,进行了动态特性仿真,并与传统PI控制进行了对比。满载下输入电压阶跃和48V输入下负载阶跃时输出电压变化情况分别如图10、图11所示。 图10 满载下输入电压变化时输出电压动态波形Fig.10 Dynamic waveforms of vo under full load when vin changes 图11 48 V输入下负载电流变化时输出电压动态波形Fig.11 Dynamic waveforms of vo under 48 V inputwhen io changes 可以看到,在输入电压和输出负载阶跃变化时,本文控制策略电压过冲更小,恢复时间更短,在动态过程中体现出更好的性能。 本文搭建了一台36~70 V输入,400 V/400 W输出的实验样机,样机照片如图12所示,其主要参数如表2所示。 图12 所提出变换器实验样机Fig.12 Experimental prototype of proposed converter 表2 实验样机参数Table 2 Parameters of experimental prototype 样机在48 V输入、400 V/400 W输出下的稳态波形如图13所示。 图13 变换器稳态波形Fig.13 Steady waveforms of proposed converter 图14为48 V输入、400 V输出下,变换器效率随负载变化曲线,当输出负载为120 W时,变换器达到最高效率96.4%。 图14 效率曲线Fig.14 Efficiency in different load condition 为了验证控制策略的有效性,对闭环电路进行了动态实验,并与传统PI控制策略进行了对比。 图15为两种控制方式下输入电压在36 V与70 V之间跳变时变换器输出电压动态响应,相关动态性能比较如表3所示。 图15 输入电压阶跃动态响应Fig.15 Dynamic response when input voltage step 表3 输入电压阶跃动态性能比较Table 3 Dynamic performance comparison when input voltage step 图16为两种控制方式下输出电流在0.05 A与1 A之间跳变时变换器输出电压动态响应,动态性能比较如表4所示。 图16 输出电流阶跃动态响应Fig.16 Dynamic response when output current step 表4 输出电流阶跃动态性能比较Table 4 Dynamic performance comparison when output current step 本文提出一种高增益DC-DC升压Cuk变换器,通过采用二极管电容单元及耦合电感,有效地提高了变换器电压增益,同时对漏感能量进行吸收,解决了传统耦合电感式高增益变换器漏感引起的开关管电压尖峰问题;为了提高所提出变换器动态性能,本文结合TSK模糊控制方法,提出一种改进模糊控制策略。实验结果表明,提出的变换器具有较高升压增益,且具有开关管电压应力小,各二极管ZCS关断,变换器输入输出侧电流连续等优点。变换器在48 V输入、400 V输出下的最高效率可达96.4%;此外,本文提出的模糊控制策略在输入电压及负载存在较大扰动时,对输出电压波动的抑制明显优于传统PI控制。1.3 稳态工作特性分析
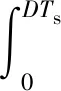
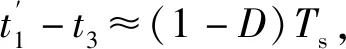
1.4 关键参数设计分析
2 改进模糊控制方法
2.1 基本工作原理
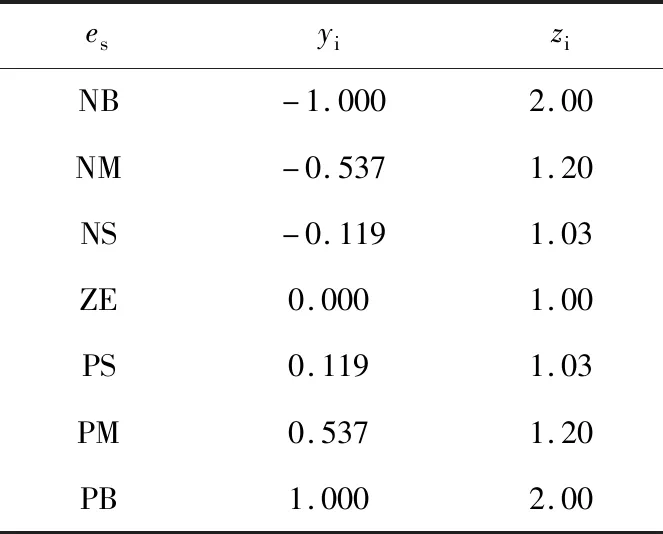
2.2 控制参数设计


3 仿真分析
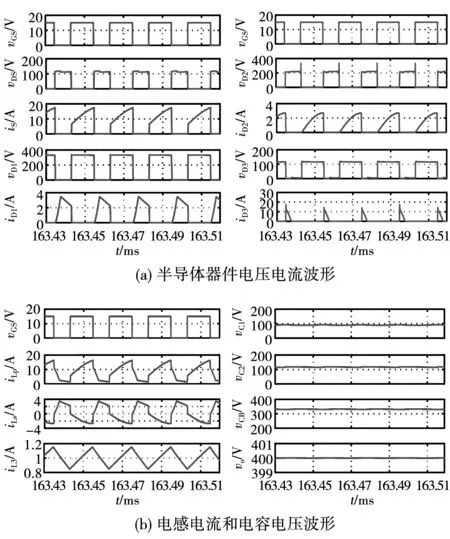
3.1 稳态特性仿真
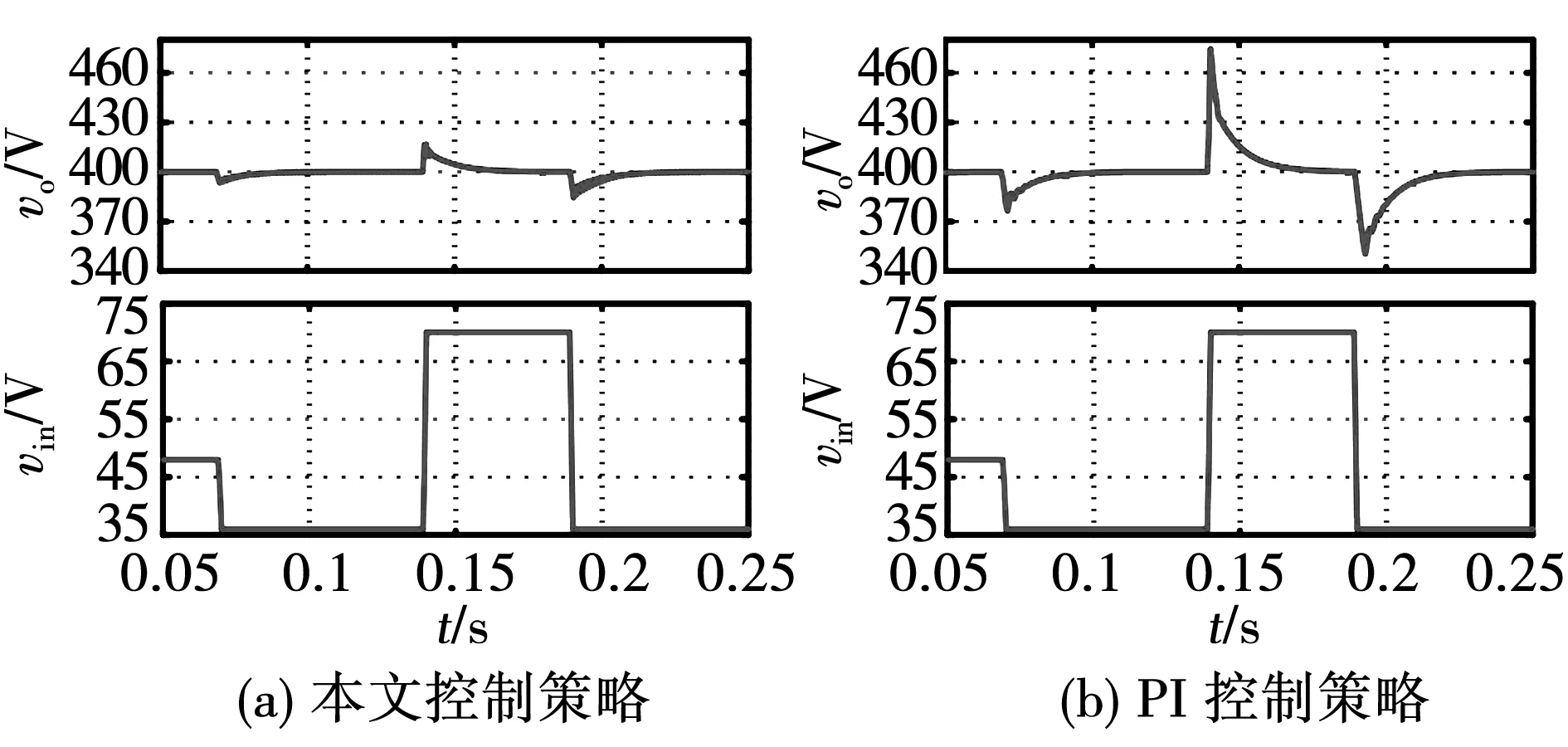
3.2 动态特性仿真
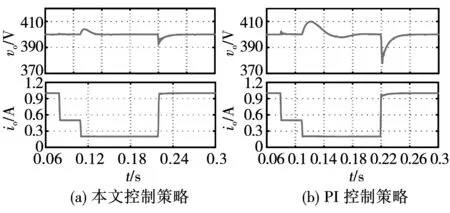
4 实验结果


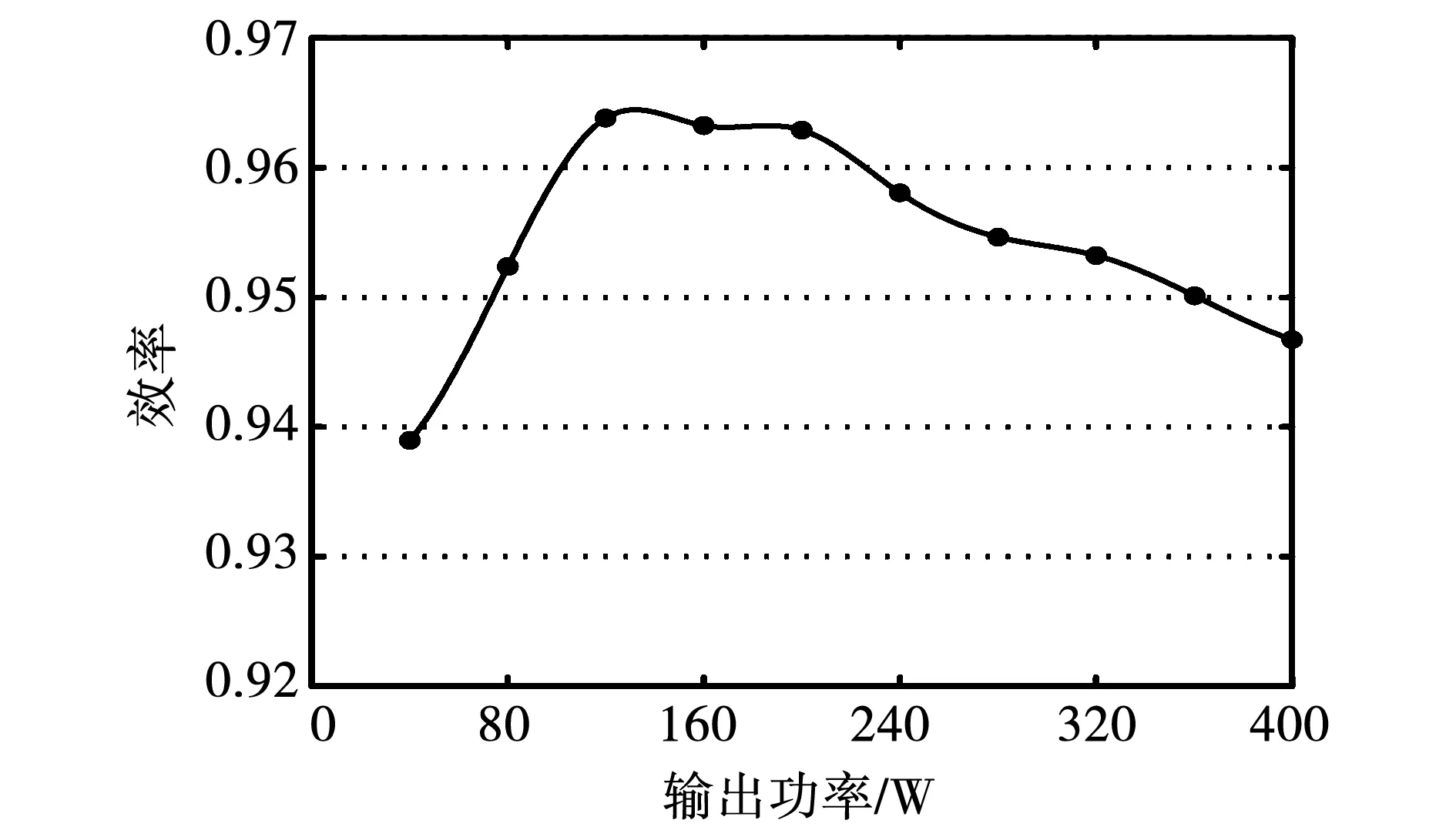
4.1 稳态实验

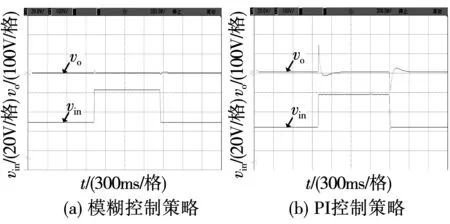
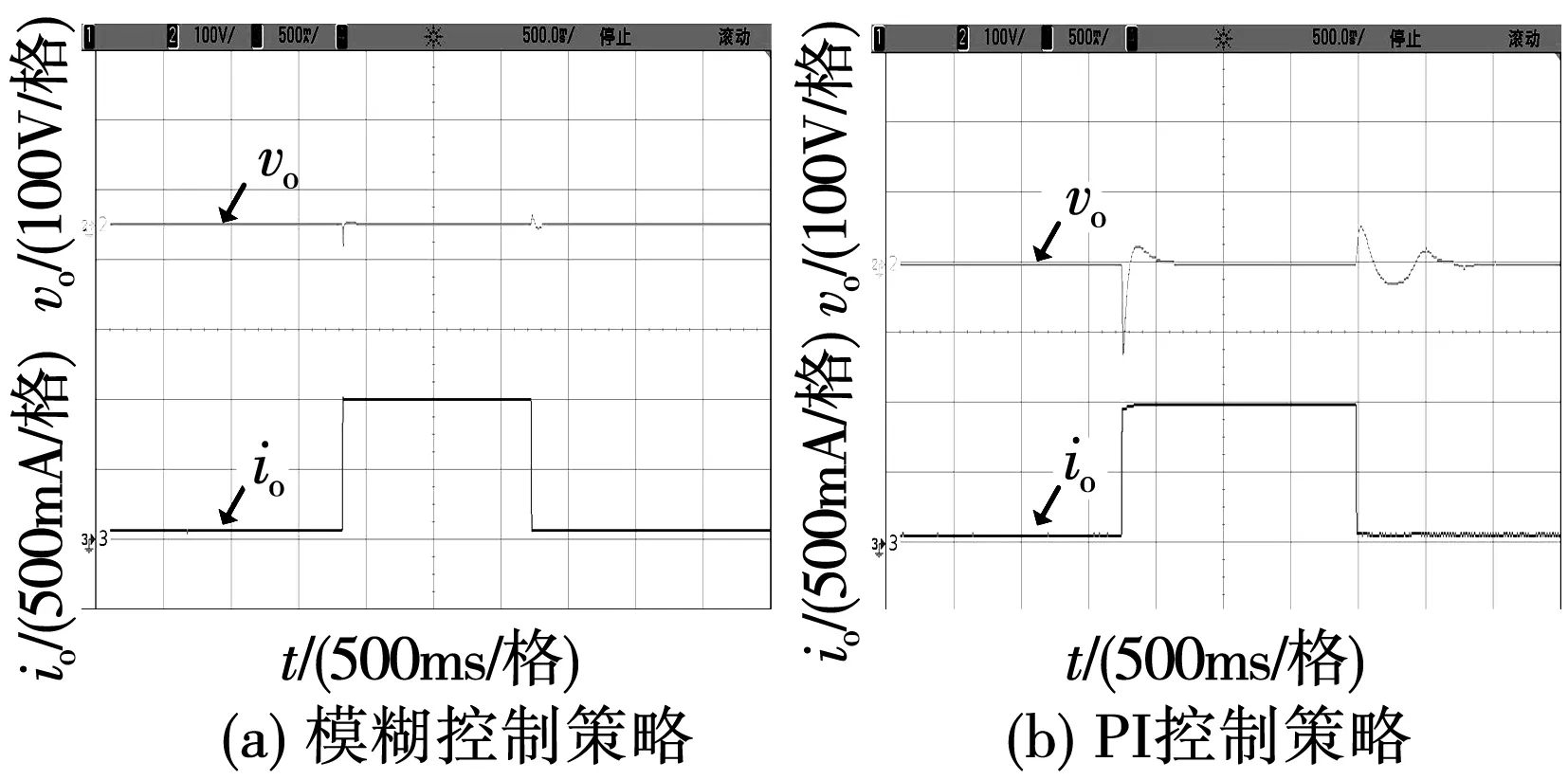
4.2 动态实验


5 结 论

