基于改进粒子群算法的微直线电机动子位置辨识策略研究

徐奇伟，龙胜，程智浩，张艺璇，支钞

(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.中国工程物理研究院 电子工程研究所，四川 绵阳 621999)

0 引 言

微机电系统(micro electro-mechanical systems,MEMS)主要将电、光、热等多种形式的能量转换成机械能输出，具有微型化、智能化、低能耗、多用途、高集成度和适于大批量制造等优点，近年来，在工业精密控制、医疗等领域应用广泛[1-4]。其中，微驱动器是微机电系统中的动力来源，将直线电机及其控制系统作为微驱动器，可以实现微米级高精确度机械运动，特别适合应用在具有空间限制要求的精密控制领域。

目前，针对微直线电机在微驱动器领域的研究，主要集中在不同结构设计和优化等方面。许孝卓等人提出了一种Halbach交替极永磁同步微直线电机，基于优化磁极尺寸提高电磁推力，但其电磁推力波动较大[5]。张铁民提出了一种基于压电式微直线电机的驱动电源方案，该电机能实现微驱动以及精密定位，具有结构简单、可靠性高、体积小等特点[6]。Alireza Safa提出了一种线性压电陶瓷微直线电机位置控制策略，采用自适应滑模策略设计鲁棒控制器，在消除颤动影响的同时，提高了响应速度并实现微纳级定位精确度[7]。

针对微直线电机位置检测的研究，李炳然等提出了一种三轴霍尔传感器检测直线电机动子磁场，但传感器安装参数对位置解算误差影响较大[8]。王辉等提出了根据高速相机相位频谱估算动子位置，但受光线影响大且集成度较低[9]。宋达辛等提出一种用于动子位置检测的同步频率提取器，该方法滤除了霍尔信号中高次谐波干扰，但检测精确度不高[10]。浙江大学卢琴芬提出基于磁链变化的位置检测策略，该策略只研究了1～5Hz运行时动子位置误差，速度和频率较低，不适合微直线电机高动态性能控制[11]。孙永倩等提出了采用扩张观测器辨识微直线电机位置，但电机系统惯性误差及振动较大影响检测精确度[12]。赵继文等提出通过非周期光栅相位差分析直线电机位置，建立直线电机动子位置和条纹图像间的关系，估算动子位移，辨识精确度为50 μm[13]。

本文针对一种新型微直线电机中动子位置辨识策略展开研究，在分析新型微直线电机结构特点的基础上，基于有限元电磁仿真分析新型微直线电机纵向磁场分布。本文基于多个隧道磁阻传感器(tunnel magneto resistive,TMR)辨识新型微直线电机的纵向磁场强度，提出一种改进粒子群算法准确辨识电机动子位置策略，该位置辨识策略能够满足精密加工制造领域对微直线驱动器高精确度、集成化的需求。

1 新型微直线电机结构分析

新型微直线电机结构示意图如图1所示。

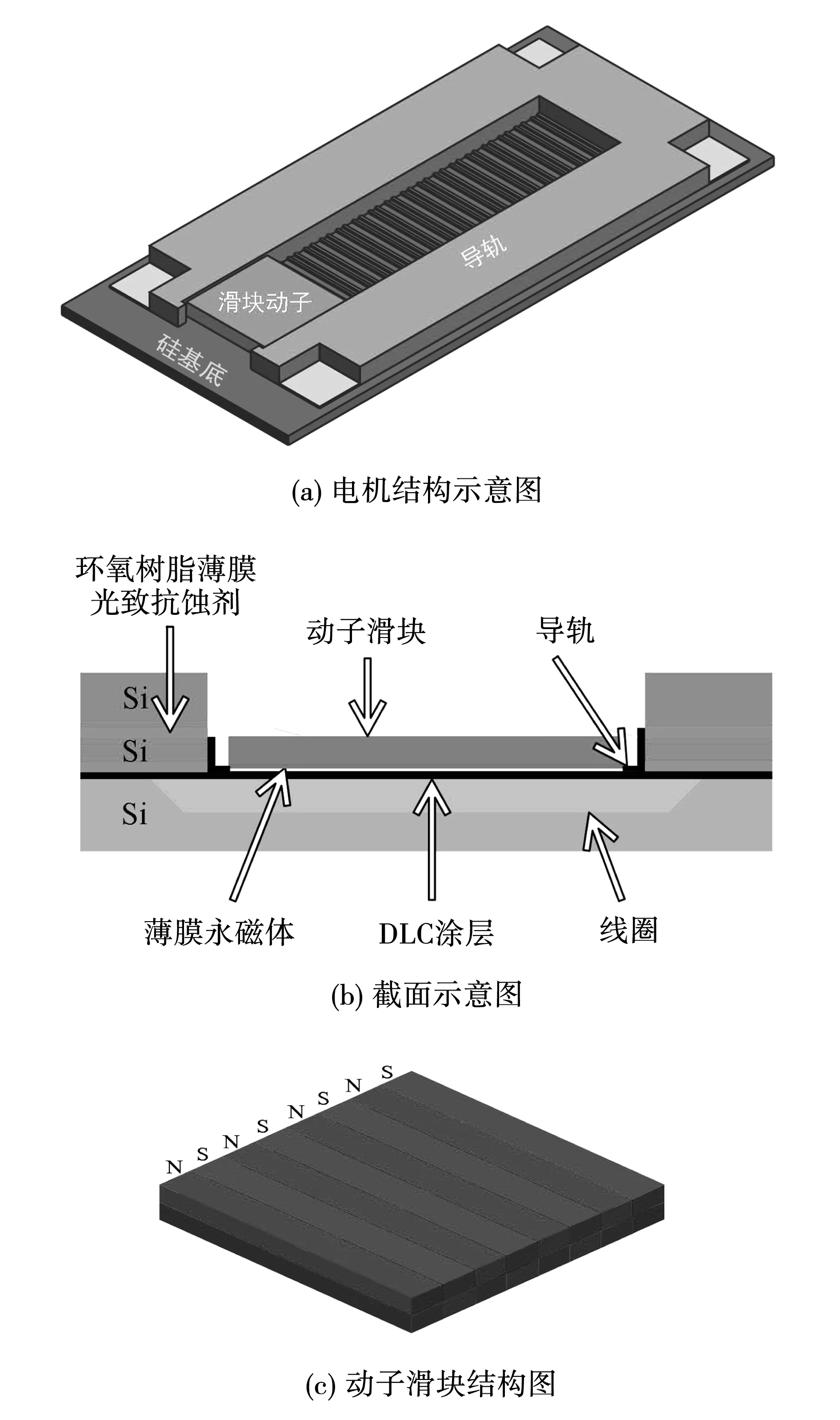
图1 新型微直线电机视图Fig.1 View of new micro linear motor

图1(a)为新型微直线电机整体结构示意图，图1(b)为新型微直线电机截面图，图1(c)为新型微直线电机动子示意图。

新型微直线电机中薄膜永磁体与绕组排列结构如图2所示，在硅基底平面排布的2组线圈A和B构成电机定子绕组。

图2 线圈绕组及动子结构Fig.2 Slider and coil winding structure

新型微直线电机工作原理如图3所示，对两相绕组A、B施加相位互差90°的正弦交流电。同相绕组A1、A2和B1、B2分别位于相邻NS磁极下，A1、A2通过的电流方向相反且处于不同磁极下，产生水平推动力方向相同，同理B1、B2水平推动力方向相同，A1、A2、B1、B2水平受力叠加推动永磁动子移动。

图3 新型微直线电机工作原理Fig.3 Operation principle of new micro linear motor

2 新型微直线电机电磁耦合分析

2.1 微直线电机中动子永磁体纵向磁场分析

为了分析新型微直线电机中电磁耦合，首先分析动子中单块永磁体产生的磁场，单块永磁体结构示意图如图4所示。

图4 单块矩形永磁体结构示意图Fig.4 Single rectangular permanent magnet

基于毕奥-萨伐尔定律，新型微直线电机中三维空间任意点P(x,y,z)处的磁感应强度受多个单块永磁体磁场共同作用，单块永磁体在xyz方向的磁场强度分别为：

(1)

式中：a、b、h分别为动子中单个永磁体的长宽高。其中参数ζ1、ζ2、K表达式如下：

(2)

(3)

K=Bz0{[ζ2(y0,a-x0,z0,z′)+ζ2(b-y0,a-x0,z0,z′)+

ζ2(x0,b-y0,z0,z′)+ζ2(a-x0,b-y0,z0,z′)+

ζ2(b-y0,x0,z0,z′)+ζ2(y0,x0,z0,z′)+

(4)

式中Bz0(x0,y0,z0)为Z轴上已知某点磁场强度。

综上可得到新型微直线电机动子纵向磁感应强度为

Bz=∑Bzs=

(5)

对式(5)进行傅里叶分析，新型微直线电机动子纵向磁感应强度的基次分量与三次分量总和占90%，因此，可将式(5)简化为：

Bz(θ)=Bz1(sinθ+ksin3θ)；

(6)

(7)

式中：y为新型微直线电机动子位置；θ为新型微直线电机动子电角度位置；Bz1为定子绕组平面处磁场强度。

2.2 新型微直线电机动子永磁体磁极排布分析

动子永磁体磁极排布方式会影响新型微直线电机气隙磁密的分布和大小。对比两种不同永磁体结构排布方式，如图5所示，图5(a)是单极性N或S间隔排布，图5(b)是双极性NS交替排布。

图5 动子单极性磁极排布Fig.5 Actuator unipolar pole arrangement

设计单块永磁体的长、宽和高分别为2、0.1和0.05 mm，两种不同永磁体结构排布下气隙磁密的有限元仿真结果如图6所示，N/S双极性永磁体交替排布时产生的气隙磁密较大。

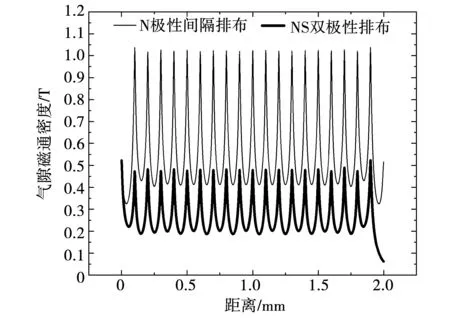
图6 N极性间隔排列与N/S交替排列的气隙磁密Fig.6 Air-gap magnetic density of N arranged spacingly and N/S arranged alternately

永磁体在两种排布方式下产生的气隙磁密z轴分量如图7所示。单极性永磁体排布时的z轴分量小于双极性永磁体排布时的z轴分量。

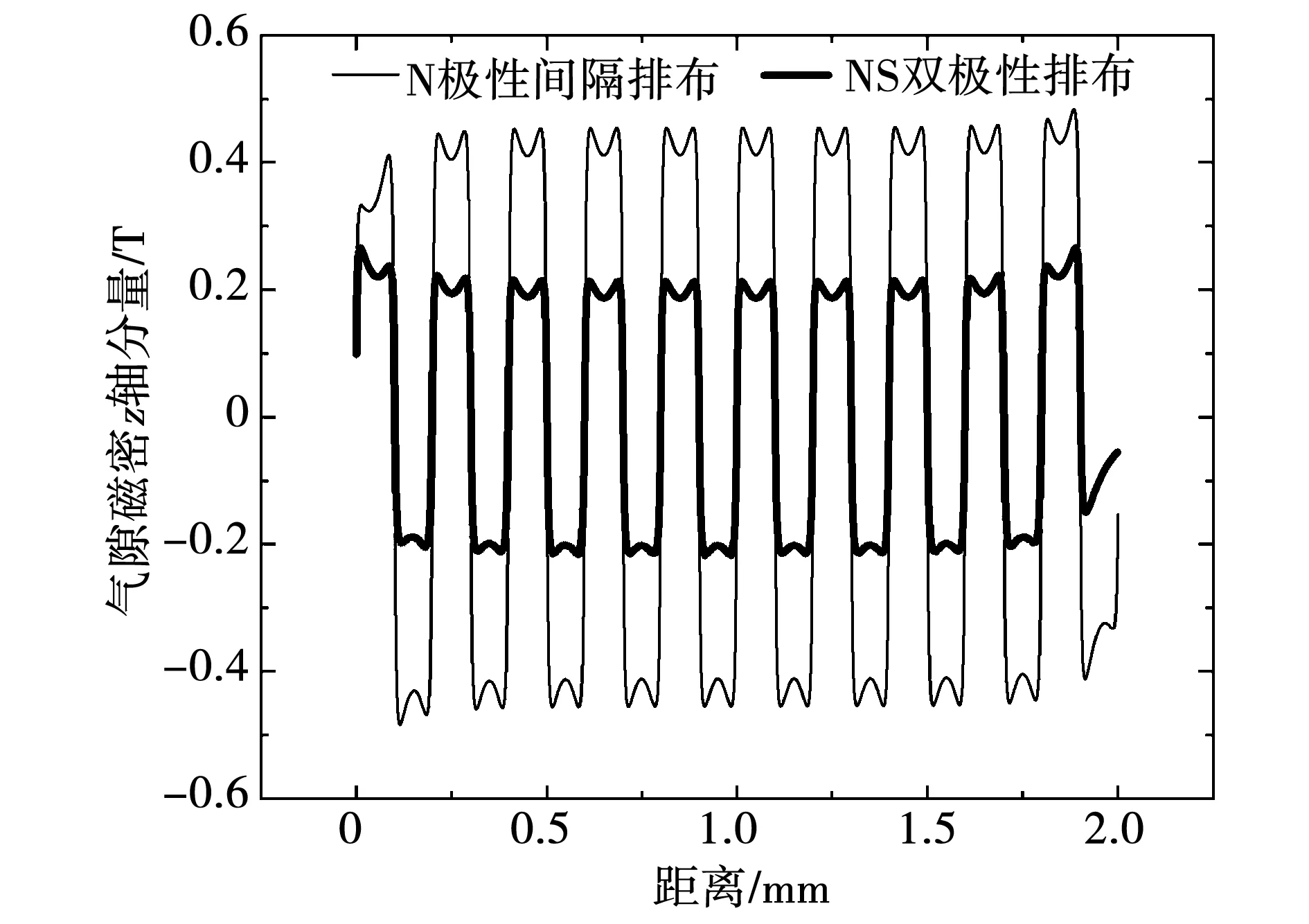
图7 N极性间隔排列与N/S交替排列气隙磁密z轴分量Fig.7 z-axial vector of air-gap magnetic density of N arranged spacingly and N/S arranged alternately

2.3 新型微直线电机动子永磁体厚度分析

新型微直线电机永磁体厚度对应气隙磁密z轴分量如图8所示。由图8可知，当永磁体厚度小于0.1 mm时，气隙磁密在单块永磁体中间部分存在不同程度的凹陷，且厚度越小凹陷程度越大，当永磁体0.1 mm及以上时，z轴分量峰值部分较为平滑。

图8 不同永磁体厚度对应气隙磁密z轴分量Fig.8 z-axis components of air-gap magnetic field with different PM thickness

进一步分析动子永磁体厚度和气隙长度对气隙磁密的影响，选取永磁体厚度0.1 mm附近0.03 mm到0.15 mm范围变化。气隙长度略大于动子和导轨间的润滑薄膜层1 μm，选取气隙长度在3 μm到8 μm范围变化。动子气隙磁密随动子永磁体厚度和气隙长度变化如图9所示。

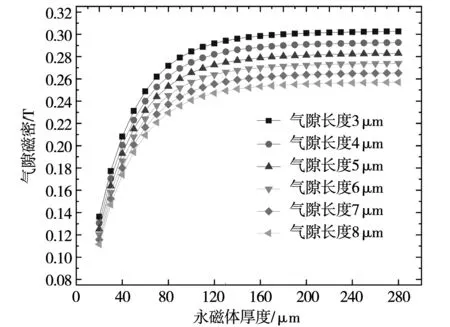
图9 气隙磁密大小随永磁体厚度变化Fig.9 Variation of air-gap magnetic density with different PM thickness

由图9可知，气隙长度越小气隙磁密越大，选择永磁体厚度0.1 mm，气隙长度3 μm，单极永磁体长度2 mm，极对数10，对动子永磁体纵向磁场强度进行有限元仿真如图10所示。

图10 新型微直线电机动子永磁体纵向磁场强度Fig.10 Vertical magnetic field strength of permanent magnet of new micro linear motor mover

3 基于TMR传感器检测动子纵向磁场的位置辨识策略

3.1 基于TMR传感器的纵向磁场检测

根据新型微直线电机电磁耦合分析，采用TMR传感器检测电机动子纵向磁场强度，对电机进行位置辨识。当TMR传感器外部磁场大小和方向变化时，TMR传感器输出电压随之变化。

TMR传感器内部由4个磁阻条组成推挽式惠斯通式桥，如图11所示。随着TMR传感器外部磁场发生变化，R1、R3阻值变化趋势相同，R2、R4阻值变化趋势相同，R1、R4阻值变化趋势相反。

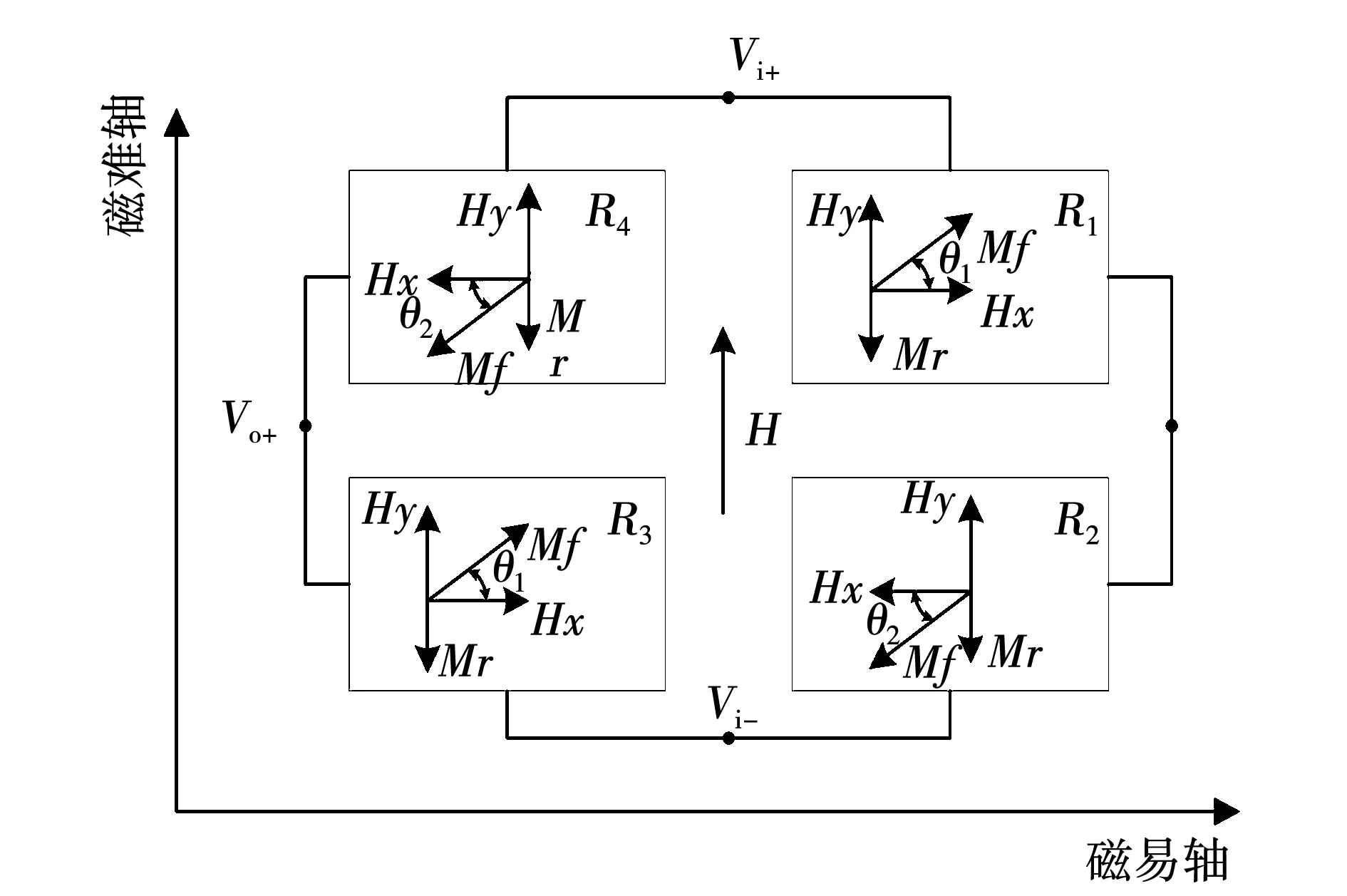
图11 TMR传感器原理Fig.11 Schematic of TMR sensor

假设电阻R1～R4随磁场H变化量为ΔRx，则在TMR传感器检测线性范围内有：

(8)

(9)

Vout=V+-V-；

(10)

(11)

由式(8)～式(11)推导输出电压与检测磁场的函数表达式，式中S表示TMR的灵敏度。

将TMR传感器输出电压与动子磁场的关系式代入动子位置与动子磁场的关系式中，可建立TMR传感器输出电压与动子位置的关系式。

3.2 TMR传感器数量与动子位置检测的关系

根据TMR传感器型号的线性检测区间、动子永磁体长度、传感器自身厚度等约束条件，优化分析设计TMR传感器安装位置，TMR传感器安装示意图如图12所示。

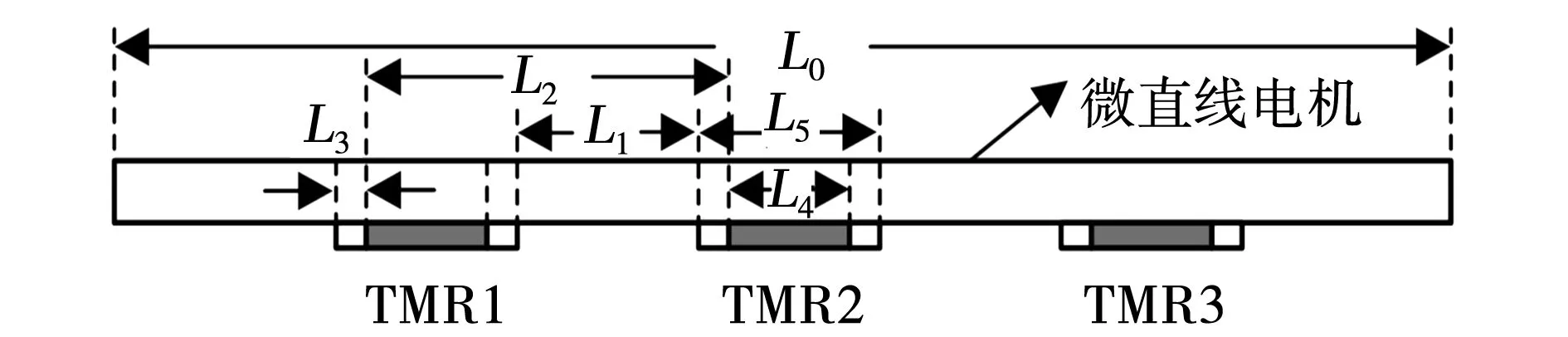
图12 TMR传感器安装示意图Fig.12 Schematic diagram of TMR sensor installation and testing

图12中：L0为微直线电机导轨总长度；L1为TMR传感器安装间距；L2为TMR传感器线性检测长度；L3为TMR传感器可检测区间；L4为TMR传感器检测死区；L5为TMR传感器长度。

根据TMR安装约束条件有：

nL5≤L0；

(12)

2L3+L4=L5；

(13)

(n-1)L1+nL5+2(L2-L3)≥L0；

(14)

L2≥2L3+L4+L1。

(15)

通过式(14)和式(15)可得

[L0-2L2-2L3(n-1)-nL4]/(n-1)≤

L1≤L2-2L3-L4。

(16)

同时，式(16)需满足：

[L0-2L2-2L3(n-1)-nL4]/(n-1)≤

L2-2L3-L4；

(17)

n≥(L0-L2-L4)/L2。

(18)

在各约束条件下，计算TMR传感器安装个数及安装位置，使动子在整个导轨均在线性检测区间，确定3个TMR传感器间距1.1 mm方案。

4 微直线电机动子位置辨识误差分析及抑制

通过检测3个TMR传感器的输出电压辨识新型微直线电机的动子位置，基于神经网络算法对新型微直线电机动子位置辨识误差进行抑制。

4.1 反向传播神经网络

微直线电机动子运动过程中，3个TMR传感器输出电压幅值随动子位置发生改变，记录3个TMR传感器输出电压幅值，并通过激光干涉仪记录当前微直线电机动子位置。TMR传感器输出电压幅值反映的是微直线电机动子纵向磁场分量大小，通过对TMR传感器输出电压信号中包含的位置信息进行解算达到位置辨识目的。传统函数拟合方法对位置解算的误差较大，而神经网络能实现对复杂非线性函数的拟合。因此，采用反向传播神经网络(back propagate on neural networks，BPNN)实现TMR传感器输出信号中包含的位置信息解码。

反向传播神经网络结构示如图13所示，3个TMR传感器的输出电压信号作为反向传播神经网络的输入，激光干涉仪显示的动子位置作为输出，通过大量数据训练神经网络。

图13 反向传播神经网络结构Fig.13 Structure of back propagate on neural networks

反向传播神经网络隐含层输入uj和隐含层输出bj的计算公式为：

(19)

bj=f(uj)，j=1,2,3…q。

(20)

式中：uj为输入层输入；wij为输入层与隐含层权值；θj为隐含层阈值；Pi为输入样本；f(uj)为神经元的激活函数。

在反向传播神经网络中，ReLu激活函数拟合过程计算量更小，且信号大于0时不会存在梯度消失情况。选择ReLu作为激活函数，即

f(x)=max(0,x)。

(21)

反向传播神经网络输出层输入lt和输出yt的计算公式为：

(22)

yt=f(lt)，t=1,2,3…m。

(23)

式中：lt为输出层输入；yt为输出层输出；vjt为隐含层与输出层权值；γt为输出层阈值。

通过反向传播神经网络得到拟合位置yt，为进一步提高新型微直线电机动子位置检测精确度，采用粒子群和改进粒子群优化算法对反向传播神经网络进行优化。

4.2 基于粒子群的反向传播神经网络算法

反向传播神经网络拟合容易陷入局部最优解，而粒子群算法可以有效弥补这种缺陷。在粒子群算法中，每个粒子的速度和方向会根据粒子自身的历史最优解和种群最优解进行调整，计算出被优化问题目标函数的适应度，并通过不断迭代以获得种群最优解。

在粒子的优化迭代过程中，速度和位置的更新公式为：

vi(r+1)=kvi(r)+c1t1(Pi-Xi)+

c2t2(g-Xi)；

(24)

Xi(r+1)=Xi(r)+vi(r+1)。

(25)

式中：vi(r)为第i个粒子在第r次迭代的速度；Xi(r)为第i个粒子在第r次迭代的位置；vi(r+1)为第i个粒子在第r+1次迭代速度；Xi(r+1)为第i个粒子在第r+1次迭代位置；Pi为个体历史最优解；g为种群历史最优解；t1、t2为[0,1]数字范围内均匀随机数；k为惯性因子，表示粒子对上一次迭代速度的维持趋势；c1、c2为学习因子，表示粒子历史最佳位置相对种群历史最佳位置的运动趋势。

在粒子群算法中，惯性因子k的取值直接影响算法搜寻最优值的能力，线性权值递减策略简单、直观，具有较好的寻优性能。采用惯性因子线性递减策略更新k值，即

(26)

式中：kmax为惯性因子的最大值；kmin为惯性因子的最小值；Rmax为最大迭代次数；r为当前迭代次数。

4.3 基于改进粒子群算法的反向传播神经网络

将神经网络中的权值与阈值作为改进粒子群中粒子的位置矩阵，粒子的适应度值为神经网络训练样本输出误差的均方差，优化目标即为均方差的最小值。

为防止神经元过多导致过拟合，以及神经元个数较少导致精确度较低，改进粒子群神经网络输入层有3个神经元，隐含层12个神经元，输出层1个神经元，激活函数采用Relu函数，种群大小一般为20至50，选取30。粒子维度为所需优化网络权值与阈值的数目，即

D=(n+m)p+p+m。

(27)

由式(27)可得粒子的维度为36。

因此第i个粒子的位置矩阵为

(28)

改进算法的目标为计算神经网络输出误差的均方差最小值，粒子适应度函数为

(29)

改进粒子群算法流程如图14所示，粒子群算法结构简单、全局寻优能力强、收敛速度快，可以很好地弥补BP神经网络的不足，提高网络收敛速度，防止神经网络陷入局部最优解。

图14 改进粒子群算法流程图Fig.14 Flow chart of improved particle swarm optimization algorithm

5 实验研究

5.1 基于TMR传感器的纵向磁场检测

采用TMR传感器检测新型微直线电机动子纵向磁场强度，通过提出的改进粒子群算法对TMR传感器输出电压与新型微直线电机动子位置的关系曲线进行拟合，反解出TMR传感器输出电压曲线中包含的动子位置信息，并将其作为新型微直线电机位置闭环控制输入给定。新型微直线电机动子和定子实物图如图15所示。

图15 微直线电机动子和定子Fig.15 Mover and stator of micro linear motor

TMR传感器和激光干涉仪位置检测示意图如图16所示。

图16 激光干涉仪检测示意图Fig.16 Schematic diagram of laser interferometer detection

TMR传感器电压输出波形如图17所示。

由图17可知，TMR传感器安装个数在3个及以上，安装间距为1.1 mm时，动子在整个行程范围内TMR传感器均有线性输出且不存在检测死区。

图17 TMR传感器测试波形Fig.17 TMR sensor test waveform

采用TMR传感器关键参数如表1所示。

表1 TMR传感器参数Table 1 TMR parameters

5.2 改进粒子群算法动子检测误差抑制

其中一个TMR传感器输出电压与微直线电机动子位置曲线拟合如图18所示。

图18 TMR传感器电压输出拟合Fig.18 TMR sensor voltage output fitting

采用激光干涉仪标定动子的位置x，并记录下动子在不同位置3个TMR传感器的输出电压u1，u2，u3，实验测得215组动子位置数据与TMR输出电压数据，其中选择200组数据作为训练样本，另外15组数据用于检测算法检测精确度。

3种新型微直线电机动位置解码算法测试误差对比如图19所示。对比分析3种位置解码神经网络的离线检测结果，其中改进粒子群优化神经网络位置解码精确度高、波动小，新型微直线电机动子位置辨识精确度误差控制在30 μm以内。

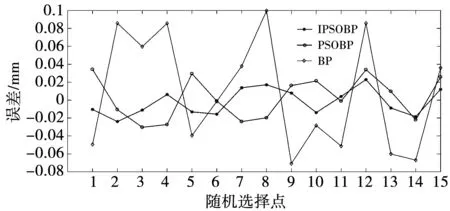
图19 3种位置解码算法的测试误差Fig.19 Test set errors of three kinds of position decoding algorithms

5.3 位置闭环控制研究

新型微直线电机位置闭环控制如图20所示。

图20 微直线电机位置闭环控制框图Fig.20 Micro linear motor position closed-loop control block diagram

图20中，Xr为位置给定；X1为激光干涉仪反馈滑块位置；X2为TMR传感器反馈滑块位置；Error1为X1和Xr之间误差；Error2为X2和Xr之间误差。

激光干涉仪显示值X1与TMR传感器估算值X2之差即为新型微直线电机位置闭环控制精确度。当TMR传感器动子位置估算值与动子给定误差小于30 μm时，则认为TMR传感器闭环控制策略精确度满足要求，最终实现只用TMR传感器的位置闭环控制。本文研究的MEMS微直线电机样机参数如表2所示。

表2 微直线电机样机参数Table 2 Micro linear motor prototype parameters

为验证提出的TMR传感器检测新型微直线电机位置策略，搭建新型微直线电机动子辨识实验平台如图21所示。

图21 微直线电机动子辨识实验平台Fig.21 Micro linear motor mover detection experiment platform

分别给电机A、B两相绕组通以幅值为0.1 A，相位相差为90°，电流频率依次为20、30、……、210 Hz，对电机运动速度进行测试，测试结果如表3所示。

表3 电机速度测试Table 3 Motor speed test

当电流频率在140 Hz以内时，电机运行平稳，动子的实际速度略小于理论速度约5%；当电流频率超过200 Hz时，电机失步现象更加明显，电机运行出现不稳定状况。

新型微直线电机闭环控制结果如图22所示，在新型微直线电机闭环控制中，将改进粒子群神经网络算法拟合后的TMR传感器电压输出与位置关系曲线作为新型微直线电机闭环控制的给定输入，调节速度环PI以及位置环P参数，动子位置反馈与位置给定误差在30 μm以内。

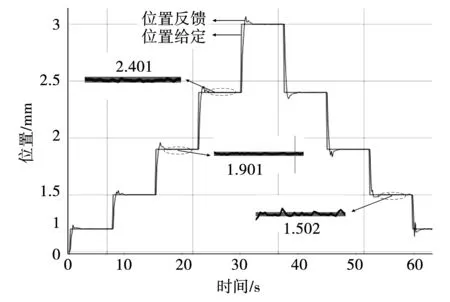
图22 MEMS直线电机闭环控制Fig.22 MEMS linear motor closed-loop control

6 结 论

本文针对一种新型微直线电机中动子位置辨识方法展开研究，研究内容及结论如下：

1)基于新型微直线电机电磁耦合分析，通过3个TMR传感器组合监测新型微直线电机动子纵向磁场强度。

2)将激光干涉仪检测的微直线电机中动子位置与TMR传感器输出电压进行曲线拟合，作为新型微直线电机位置闭环给定输入，得到电机控制结果，与激光干涉仪检测结果进行精确度校对，提出了一种改进粒子群算法将动子位置辨识精确度误差控制在30 μm以内。

3)提出采用TMR传感器对新型微直线电机动子位置辨识策略，在满足电机和系统小型化集成的要求同时达到较高的位置辨识精确度，实现新型微直线电机位置精确度30 μm的闭环控制。