变惯量飞行塔类游乐设施降低旋转驱动功率方法探讨

卢镇海，庄胜堂

（广东金马游乐股份有限公司，广东中山 528400）

0 引言

飞行塔类是游乐设备的一种类型，主要实现在一定高度下的升降或绕垂直旋转的运行形式［1］。变惯量飞行塔类游乐设施（旋转飞椅系列飞行塔游乐设施）主运动为乘人装置绕垂直轴一边升降一边旋转，乘人部分采用环链或钢丝绳吊挂，多为单人座椅或双人座椅的飞行塔类游乐设施［2］。相较于其他飞行塔类游乐设施，其最大特点是运行过程中转动惯量随座椅摆开越来越大，直至座椅到达最高点，此时惯量也最大。

赵九峰［3－4］对游乐设备通过解析计算方法对驱动机构功率计算与选型做了介绍，基于ANSYS_WORKBENCH 给出了自控飞机回转机构驱动功率的计算及电机选型的流程；胡泽林［5］则对某个固定惯量的飞行塔游乐设施旋转驱动选型计算做了分析。但各类文献在计算旋转驱动功率时都采取恒定旋转角加速度方案，并据此计算得到功率，计算方法过于保守，不利于提高设备的经济性。在不增加设备运行时间的前提下，采用更为经济的加速度控制策略降低旋转驱动功率，提高设备的经济性，显然有较大的实用性价值。

本文建立了旋转驱动模型，通过分析变惯量飞行塔游乐设施运动学、动力学等特点，结合其运动过程惯量变化特点，给出了不同阶段给定不同旋转角加速度，进而合理降低旋转驱动功率，提高设备经济性的方法，为此类游乐设施驱动选型提供了新思路。

1 分析计算

1.1 基本运动分析

常规变惯量飞行塔类游乐设施主要由塔架、滑行架（座舱承载体）、驱动装置等组成。其主运动分为沿着塔架的垂直升降运动及绕塔架中心的旋转运动两部分，如图1 所示。

图1 飞行塔类游乐设备

本类游乐设施沿塔架垂直运动相对简单，非本文关注重点，故而下文不再讨论。绕塔架旋转运动一般使用回转支承作为旋转支承体，动力源则使用电机，而驱动类型主要有摩擦传动和齿轮传动两大类。后续将以搭载回转支承作为承载体，电机齿轮传动驱动系统的变惯量飞行塔游乐设施展开讨论。

设备绕塔架旋转运动过程中，随着旋转速度的不断增加，座椅离心力越来越多。在离心力作用下，绕着吊点中心将会逐渐展开，直至达到最高点，如图2 所示。

图2 飞行塔类游乐设施旋转过程

研究座椅加速摆开过程，取极小时间间隔t0～t1进行分析。设t0时刻设备的旋转转速为ω0，此时的角加速为ε0，则根据运动学基本公式可得［6］t1时刻的旋转角速度为：

座椅在摆开过程中，一般运动状态较为平稳，则座椅的重力与座椅的离心以及吊点的拉力相互平衡，如图3 所示。

图3 座椅摆开过程受力分析

考虑到t0～t1时间间隔小，近似地以t0时刻座椅摆开位置的θ0替代t1时刻座椅的摆角，则t1时刻座椅的旋转半径满足：

式中：g为重力加速度。

1.2 旋转过程的阻力与阻力矩

此类设备在运行过程中，主要的阻力矩［8－10］有惯性阻力矩、回转结构的摩擦阻力矩、空气阻力矩。即旋转加速过程任意时刻所需驱动力矩为：

式中：M1为t1时刻所需的旋转加速力矩；M2为回转结构的摩擦阻力矩；M3为空气阻力矩。

一般而言，详细设计阶段因考虑重量不均匀系数k，即所有关于质量相关计算都需要乘以系数k，考虑到游乐一般为对称且均匀结构，此处计算取k＝1。

在t1时刻，惯性的力矩为：

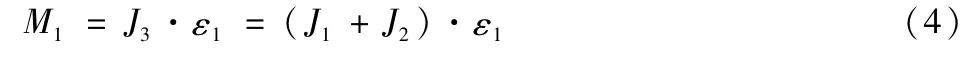
座椅转动惯量为：

式中：n为座椅的数量；m为座椅的质量（此处一般取满载座椅：座椅＋乘客，下同）；r1为t1时刻的座椅旋转半径；ε1为t1时刻座椅、固定部分转动的角加速度；J2为固定部分的惯量。

摩擦阻力矩为：

式中：m2为固定惯量部分质量；rf为回转支承转动半径；μ为回转支承摩擦因数。

座椅风阻力矩为：

式中：A1为座椅迎风面积。

一般而言，固定部分因为旋转直径较小，故其风阻力矩与摩擦力矩和座椅力矩（座椅摆开后）相比数值较小，一般可不考虑。但实际结构若此部分力矩无法忽略时，可参照座椅风阻力矩计算方法进行计算。本文不考虑该部分阻力矩。

1.3 电机最小驱动力与功率

t1时刻电机需要的最小输出力矩为［7］：

式中：z0为驱动数量；i为齿轮速比；η为齿轮传动效率。

t1时刻所需电机的最小功率为［7］：

1.4 加速度控制与电机功率

通过上述分析可知，变惯量飞行塔类游乐设施在其加速过程当中，电机输出力矩主要用于克服阻力矩（惯性阻力矩、回转结构的摩擦阻力矩、空气阻力矩）。在相同的加速时间内，任意时刻t的摩擦力矩为：

显然，整个驱动过程全程保持不变。

座椅风阻力矩为：

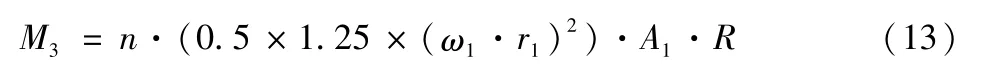
座椅平稳运行时，座椅的离心加速度a 与重力加速度g 以及摆角θ满足如下关系：

即座椅摆动各个位置的速度基本一致，则座椅风阻力矩全程基本相同。

惯性阻力矩为：

座椅处于相同位置时，其旋转惯量就一致。故改变旋转角加速度即可改变惯性阻力矩，进而改变所需电机的力矩。

由上述分析可知，假设相同加速度时间前提下：座椅摆角较小时，可适当提高旋转角加速度；座椅摆角较大时，应适当减小旋转角加速度。

按此思路设计，可在不增加运行时间的前提假设下，有效降低设备的驱动功率，提高设备的经济性。

根据上述分析，可供选择的角加速度控制曲线如下。

（1）构造多段斜率角加速度控制曲线

构造多段斜率角加速度控制曲线如图4 所示。当设备运行功率较大时，考虑到启动时电机电流较大，可考虑使角加速度从0 开始增加，以降低系统的启动电流；然后慢慢增大旋转角加速度运行到惯量较大位置后，再逐步降低旋转角加速度。当然，如果设备功率小，选取多个恒加速度分段控制也是一个有效的方式。

图4 多段斜率角加速度控制曲线

现今，国际一流品牌变频器（如西门子、施耐德等）都支持使用多段斜率驱动方式，该类变频器内甚至还有复杂的控制曲线，对于变惯量飞行塔游乐设施旋转控制而言，基本上可以满足使用需求。

（2）现有的数学函数

使用现有数学函数作为旋转角加速度控制曲线，也是一个备选方案。对于本类设备而言，旋转角速度曲线使用Sin 函数（角加速度曲线为Cos函数）控制也基本上可满足要求。Cos函数加速度控制曲线如图5 所示。

图5 Cos函数加速度控制曲线

使用三角函数控制缺点是启动电流较大，选择双曲正切函数（tanh）可避免该问题（注意此时应控制角速度），合理分配速度区间可满足使用要求。双曲正切函数函数如图6所示。

图6 双曲正切函数函数

（3）其他方法

如果上述方法仍无法满足使用要求，可进一步借助仿真软件进行动力学仿真后，根据惯量变化特点，借助MATLAB、SolidWorks等软件构造更为复杂的角加速度控制曲线。动力学仿真得到的角加速度控制曲线如图7 所示。图中，某个承载72人的变惯量飞行塔的角加速度控制曲线，起点角加速度为0，避免电机启动电流太大。之后逐渐增加加速度，达到大惯量区域后再逐步降低。采用此方案，除了可以降低旋转驱动功率外，还能使得整个过程角加速度过渡平滑，减少运行过程中的冲击，提高设备运行的稳定性。此方法需要根据设备具体参数详细计算，故不具体展开讨论。

图7 动力学仿真得到的角加速度控制曲线

1.5 实例分析

某个承载72 人的变惯量飞行塔类游乐设施，其主要参数如表1 所示。

表1 某变惯量飞行塔类游乐主要参数

现按2 种不同驱动加速度计算，如表2 所示。

表2 不同加速度控制方案

按式（1）～（11），借助Excel，按Δt＝0.1 s积分步长进行离散，计算全加速过程设备所需的最大旋转驱动功率，并统计。

整个运行过程，设备的旋转角速度以及旋转角加速度曲线，如图8 所示。图8（a）为方案1 的角加速度－时间控制曲线，角加速度全过程为恒定值；图8（b）为方案2 的角加速度－时间控制曲线，角加速度全程为不定值的Cos 函数曲线，角加速度值先大后小，与设备运行惯量变化趋势相反。

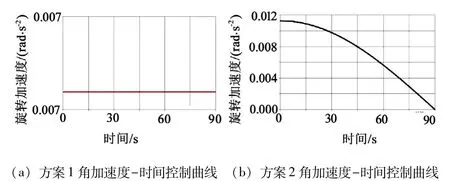
图8 旋转角加速度曲线

旋转角速度曲线如图9 所示。图9（a）为按方案1 恒定加速度控制思路得到的角速度－时间曲线，速度呈线性变化趋势；图9（b）为方案2 的角速度－时间曲线（Sin 函数曲线），速度值变化先快后慢，变化趋势较为缓和。

图9 旋转角速度曲线

驱动功率曲线如图10 所示。

图10 驱动功率曲线

功率计算结果如表2 所示。对比可知，采取方案2，旋转驱动功率显著降低。

表2 不同加速度控制方案计算最大功率

2 结束语

本文通过解析计算方法，建立变惯量飞行塔类游乐设施旋转驱动模型，分析其运行过程的运动学、动力学等特点。经过理论分析后发现，此类游乐设施因惯量在运行过程中不断变化，旋转角加速度若与惯量变化趋势匹配：小惯量阶段选择大旋转角加速度，大惯量阶段选择小旋转角加速度；在设备运行过程中，不增加设备运行时间的前提下，可有效地降低设备所需要的最大旋转驱动功率。本文为变惯量飞行塔类游乐设施计算旋转功率时提供了新思路，可有效降低设备旋转功率，以提高设备的经济性。