磁致伸缩换能器谐振腔内介质密度声场分析*
汪建新,王晓明,晋 康
(内蒙古科技大学机械与工程学院,内蒙古包头 014010)
0 引言
热声制冷是一种新兴的绿色技术,也是满足各种制冷需求的替代技术[1]。作为一种新兴的有前途的技术,其比传统的蒸汽压缩制冷系统具有诸多优点[2],如没有运动部件,不需要外来材料,以环境友好的气体如空气或氦气作为工作物质,可靠性更高。热声制冷机将声能转化为冷量,封闭谐振腔中的气体在声能的作用下产生驻波。驻波引起整个热声堆的温差。冷热热交换器位于热声堆的两侧,冷热交换器利用二次循环流体从冷室吸收热量。并且冷热交换器周围的气体吸收热量,并通过堆的小孔被泵送到热热交换器[3]。在其作用下,气体微团不断进行收缩与膨胀与热声堆进行热量交换[5]。
磁致伸缩换能器[4]作为新型的换能器将电磁能转变为机械能,可以满足微型热声制冷机驱动所需要的大振幅与高频率的要求。利用磁致伸缩换能器的磁机耦合特性,通过改变对换能器施加交变电流激励和频率的大小来使谐振腔内获得最大的声压值,使得整体机获得高效的制冷量。
对于谐振腔的分析大多是对谐振管时间位移激励或端口压力[6],对其进行声场内的数值模拟研究和流体力学分析,得到谐振腔内一些参数变化规律[7-13]。与之前的研究工作不同,本文对谐振腔内的气体施加不同的基础压力,并利用有限元软件ATILA 进行分析,计算不同谐振腔压力下由换能器驱动谐振腔产生的声压及辐射板位移值。
1 理论基础
将谐振腔内的空气提取出来进行简化,以柱坐标为基本坐标进行描述,径向半径为r,极角为θ,轴坐标为Z。由三维空间波动方程以及拉普拉斯算符相结合计算求解,为确定定解值,把径向和轴向的刚性壁面作为边界条件进行转化求解,最终得到关于Z、θ以及R的3个常微分方程[14]。
热声制冷机谐振腔内部存在驻波波形,对Z 方程进行求解为:
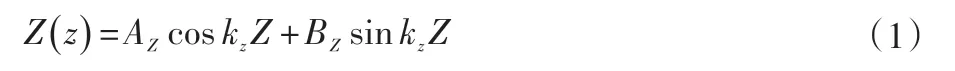
式中:A和B分别为声量和密度的幅值;Z为阻抗。
求得Z方向上的质点速度为:
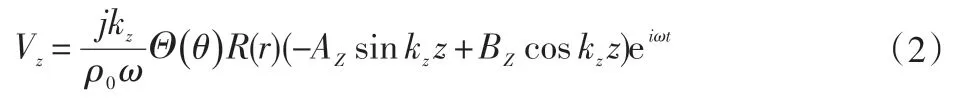
式中:R(r)为声阻;ρ0为大气密度;为柱贝塞尔函数,柱贝塞尔方程为周期函数,其解为:
对R的常微分方程进行适当变换,令krr=x,则方程转化为:

其中,x 是柱面坐标以及半径的替代。式(3)作为标准的m阶的柱贝塞尔方程,其一般解为:
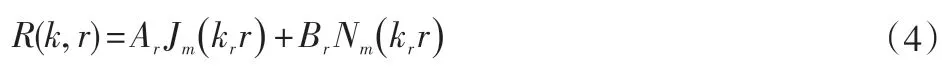
式中:R(k,r)为柱坐标下的坐标和半径的声阻;Nm为响度。
可以求得管中的声压解为:

对应径向速度为:

式中:θ和φm分别为柱面坐标和坐标角。
刚性管壁条件下kr有一系列的特定数值,表1 所示为部分的数值,其中m和n两个正整数可以表示为kr=kmn。

表1 柱贝塞尔根值
根据柱贝塞尔根植,其中的m、n 表示圆柱形管的(m,n)次简正波可表示为:

由声学理论可知,当声源处所产生的频率大于圆管中简正频率时,会产生高次波,使得谐振管内的波不纯粹。需要确定谐振腔管内的截止频率,确保管中只能激发出单一的平面波。
在常温下,空气声速为347 m/s,谐振腔长度为170 mm,谐振腔半径为0.015 m,所以求得圆柱形管中的平面波截止频率:
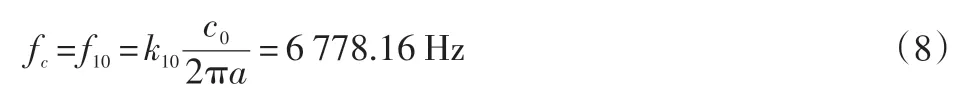
在实际的热声制冷机的谐振管内的声场频率一定要小于沿z轴轴线的截止频率6 778.16 Hz,使得谐振腔内的轴线方向有单一的平面波,防止色散发生而产生高次谐波。磁致伸缩换能器为谐振腔提供的能量大小可以提高热声制冷的制冷能力,当换能器驱动辐射板振动,谐振腔内可以产生足够大的声场强度。本文通过有限元软件ATILA 对换能器进行不同基础压力下的不同频率的仿真分析。
2 仿真分析
通过建立磁致伸缩换能器的仿真模型如图1所示,磁致伸缩换能器主要由T-D 材料棒、线圈、辐射版、外壳以及空谐振腔组成。模型整体长度为300 mm,其中,谐振腔长度为170 mm,辐射板厚度为5 mm,T-D 材料棒的长度为90 mm,直径为16 mm,线圈匝数为350。换能器内T-D材料棒在线圈提供的交变磁场内伸缩振动,直接推动其前端的辐射板做同样的往复振动,从而在谐振腔内产生声场。

图1 磁致伸缩换能器仿真模型
利用仿真模型用有限元仿真软件ATILA 进行仿真分析,在ATILA 当中完成机构建模如图2 所示,选 用“AXISYMMETRIC”轴对称模式的命令形式,为的是防止过大的计算量;线圈所处设置磁域空间AIR MAG,导磁率为1;换能器以及辐射板给予材料钢,空腔内赋予AIR FLUID;选择分析类型为谐响应,其主要命令形式为“HARMONIC”,可以准确的分析各个频率下激励线圈对谐振腔内部产生波形与声压大小;分析频率区间设置为1 000~8 000 Hz,步长为1 000 Hz。

图2 磁致伸缩换能器谐振腔有限元模型
在谐振腔内部要达到稳定的驻波声场,对流换热是经过气体微团不断膨胀收缩与板叠交换而来的。制冷能力的提高指的是单位时间内有更多的气体微团进行热量交换。谐振腔内的声压大小由气体密度来实现,谐振腔内部压力值与气体密度对应值如图3所示,由图3可以看出随着气体密度随着系谐振腔声压的增大而增大,几乎成线性关系。
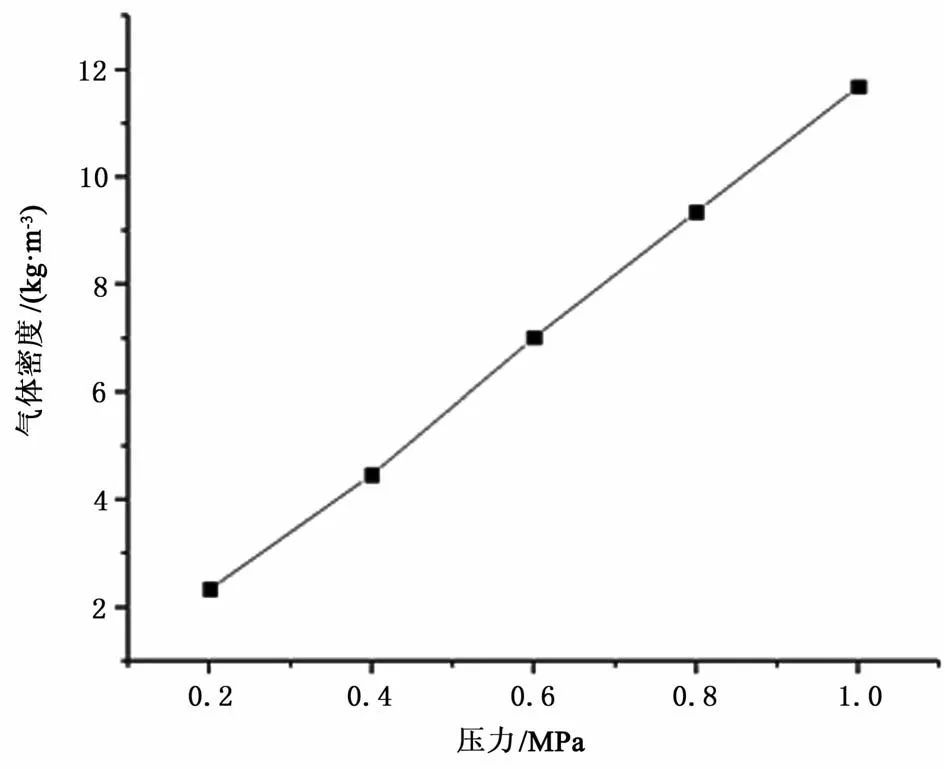
图3 谐振腔内压力-气体密度对应
将上述不同压力值下的气体密度参数放入有限元分析软件ATILA 软件前处理单元中的AIR FLUID 中进行材料模块设置。得到谐振腔在各基础压力下对应的驱动频率1 000~8 000 Hz之间的声压值如图4所示,图4(a)的声压折线图与图4(b)的声压映射曲面图可以看出在谐振腔内在1 000~8 000 Hz 的频率区间内获得的最大声压值也是呈现增大趋势的;最大值出现在基础声压在1.0 MPa 的8 000 Hz 驱动频率上,高达359.97 Pa;而且在基础声压为0.8 MPa的3 000 Hz的驱动频率时,谐振腔内声压值远远大于同等条件下其他基础声压下此频率的声压值。

图4 各基础声压下激励频率-谐振管内声压对照
如图5 所示,谐振腔声压的最大值并未随着基础压力的提高而一味提高。而是在基础声压为0.6 MPa、激励频率为2 000 Hz时达到最大值。且与谐振腔压力为基础大气压时在相同条件下获得的声压值相比有很大程度的提高,达到了6.8倍之多。但是随着基础压力的提高,对应出现最大声压值时的激励频率有所降低。这主要是因为随着谐振管腔体内基础压力的提高,作用在辐射板上的力也同时增大了,这改变了辐射板在激励作用下的响应状态所致。

图5 各个基础声压下驻波形态时对应的最大声压和激励频率
对模型进行激励频率—输出位移仿真,得到位移结果如图6 所示。从图中可以看出在激励频率为1 000~9 000 Hz的范围内,辐射板位移随激励频率的增大而依次增大;当超过9 000 Hz 时,辐射板位移会呈现出内外交替的位移变化,且其位移变化值在激励频率为9 000 Hz 时的位移内。且在9 000 Hz 激励频率时,辐射版位移最大,此时磁致伸缩换能器谐振腔内声压最大,可以有效提高热声制冷机的能效。
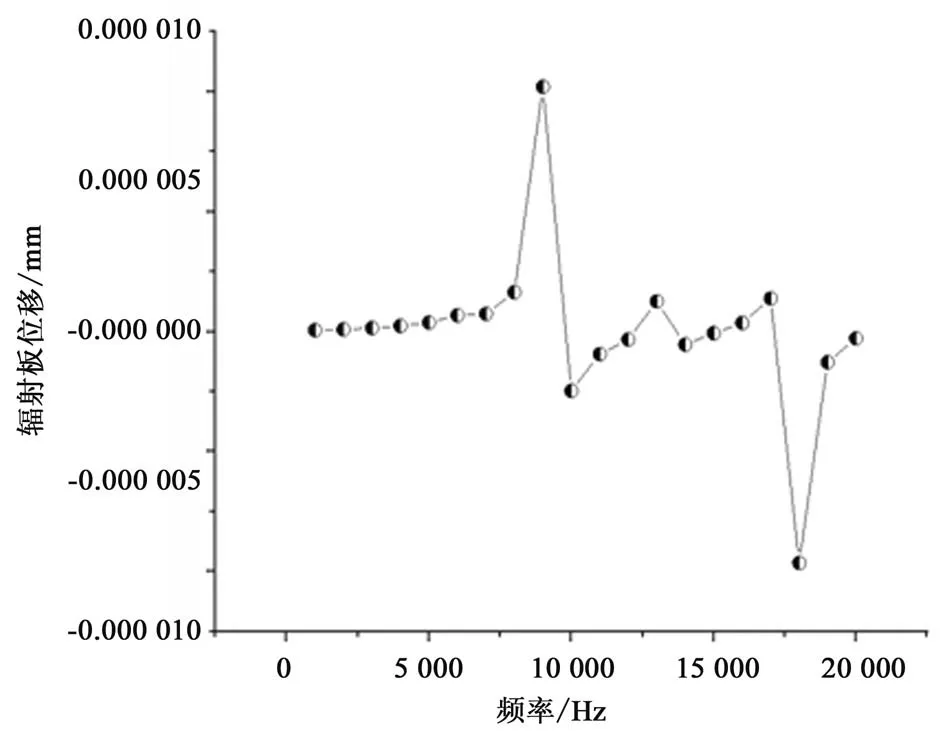
图6 整体模型激励频率—输出位移输出
3 结束语
本文利用有限元分析ATILA 对其进行磁-机耦合与气-固耦合分析,激励电流保持不变的条件下,在谐振腔内加载不同的基础压力,在激励频率1 000~8 000 Hz 下,获得各个基础压力下较为稳定的平面驻波,为热声制冷机谐振腔的声场分析提供了对比数据,提高了制冷能力。
在谐振腔内加载基础压力会影响辐射板在激励下的响应特性,导致谐振腔声压大小发生变化。随着加载基础声压的增大,谐振腔内产生的声压值也随着增大。需要根据分析结果选择最优的加载压力与驱动频率的组合。
整体模型激励频率-输出位移显示出,在激励频率为1 000~9 000 Hz 的范围内,随着频率的增大而增大,且在1 000~20 000 Hz的范围内,在激励频率为9 000 Hz时辐射版位移最大,谐振腔内声压最大,可以有效提高热声制冷机的能效。

