土石坝漫顶溢流在小型水库运行管理中的应用

王 远

(乌苏市兴源水务有限公司，新疆 塔城 833000)

21世纪以来，伴随着可靠性数学、水力学与随机水利学的不断发展，其研究成果已经逐步形成了水利工程风险分析理论，其研究成果已经逐步应用水利工程之中[1-2]。而漫坝风险分析模型成为水利工程中管理学科的重要组成，是实际水利工程中分析缺水水库的防洪与兴利之间的矛盾的理论基础[3-5]。

对此，本文在漫坝分析理论的基础上，综合考虑水库漫坝的洪水、风浪、库容和泄水四方面的不确定性因素。建立新疆某水库大坝在洪水系列与风浪系列联合作用下的漫坝风险模型，在确定的调度方案下，在保证洪水与风浪作用下的漫坝风险以及可靠的安全性的前提下，优化该水库的汛线水位，达到提高水库的整体兴利的目的。同时可为相应的水库管理提供科学合理的决策依据。

1 水库简介与不确定性分析

1.1 水库基本参数

本文研究的水库位于新疆某地区，是集合防洪、供水、灌溉、发电以及养鱼的综合性水库。在大坝的分类中属于Ⅱ水库。该水库的总库容为1.81×109m3；控制的流域为300 km2；设计水位为106 m；蓄水位109 m；校核洪水位110 m；浪墙顶高程113 m；坝顶高程111.7 m；水库的下游河道安全泄量450 m3/s。

1.2 不确定性

在随机数学的概念中，不确定性有被称为随机性，在工程中指的是的不可控的条件。因此在本文的研究中，将水库的洪水、风浪、库容、泄流能力都看作不可控的条件，定义为随机变量。

1.2.1 洪水

在工程水利中，发生在某一频率下的洪水是随机事件，根据该水库的相关建设资料，其设计的洪水过程线如图1所示。

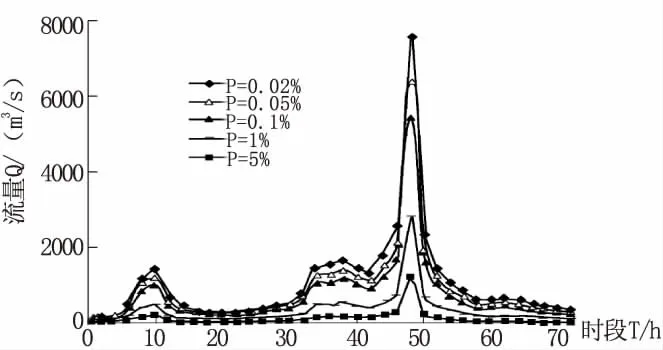
图1 不同频率设计洪水过程线

通过假设检验，设计的洪峰满足的概率密度函数为

f(Q)=0.052 87×(Q-100)0.862 8e-0.000 685 8×(Q-100)

1.2.2 风浪

在自然界中，自然风的风速与风向分布是随机的。因此在水库中，风引起的波浪爬高的高度也是随机变量。在水库的漫坝风险中，，只有在发生洪水的时候，吹向坝体的自然风才能起到推波助澜的作用，此时分析风浪的影响才是最有效的。通过对该水库近40 a的风速进行统计分析来看，该水库在汛期期间，风速位于6.8～18。7 m/s之间。经过统计分析可以知道，均值为12.12 m/s，均方差为3.055.采用K-S检验之后，可知主、副承受的有效风系列，符合随机数学中的I型分布情况。

1.2.3 库容

在传统的水利水电分析中，将库面积以及库容认为是确定的数值。而从实际的工程来看，他们均是随机变量。对于同一个水库工程而言，不同的水库测绘人员所测量得到的等高线图会存在一定的差异。并且及时在相同的等高线条件下，计算方法或者计算设备不同，其计算得到的库面积以及库容也会存在差异。并且，在洪水期间导致的冲淤也会对对库容产生影响。因此在实际工程中，想要得到库容的准确值十分困难，如图2和与图3所示分别为水位与库面积、水位与库容之间的关系曲线，其只能表达出库容与库面积均值的含义。通过统计结果可知，库容函数满足正态分布曲线。

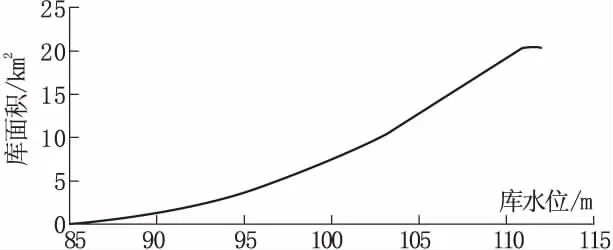
图2 水位-库面积关系曲线

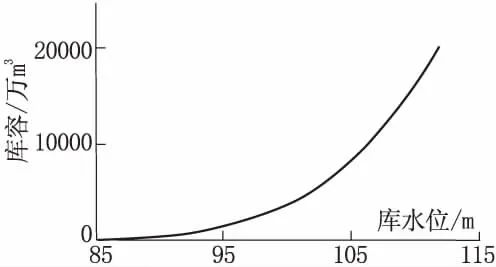
图3 水位-库容关系曲线

1.2.4 泄流

本文研究的水库洪洞与爆破副坝水位—泄流关系如图4所示，对于泄流而言，其不确定性主要体现在测量误差以及粗糙率的取值不确定性造成的。通过对该水库工程不同水位下的泄流能力进行统计分析，其在分布上满足正态分布。

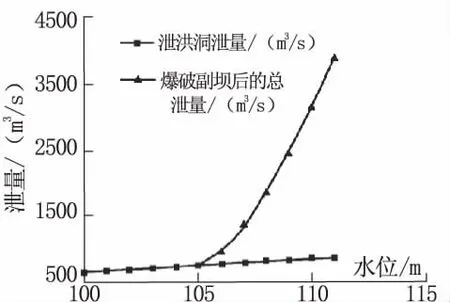
图4 水位-泄量关系

2 漫坝风险模型的建立与分析

2.1 漫坝风险模型

根据对该水库的不确定性分析后，建立该水库的漫坝风险模型，模型具体表达方程如下：

R=P(Z(t)≥Zc)=P(Z0+Hmax+e+Rp≥ZC)

(1)

式中：R为洪水与风浪同时作用下的漫坝风险；Z0为汛水位；Hmax为洪水增加高度值；e为水面风高度；Rp为波浪爬高；Zc为临界高程。

当洪水[Qi-1，Qi]与风[Wi-1,Wi]事件同时出现事，风险为：

Pij=P(Z0+Hmax+e+Rpij≥ZC)

对抗系列洪水和风事件时,总风险为：

在实际工程中，风是随机变量，因此Rp是一个复合变量，在风速[Wi-1,Wi]时，Rp的概率为：

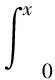
fRp(Rp)表示的是瑞利概率密度函数，因此可以得到Rp的函数为；

对于单一的漫坝风险而言，其主要求解的是Z(t)的值，在这个过程中，需要对水库的调洪进行相应的计算。正如前文所述，调洪验算是一个随机过程，并且水库的需水量以及水位满足马尔科夫矩阵与独立的增量条件，对此可以得到水库调洪的相关计算公式如下：

(2)

H(t0)=H0

(3)

式中：H表示为平均蓄水位；H0表示为起调水位；H(t0)为初始条件；Q(t)为洪均值过程；q(H·C)为泄洪流量的平均值；F(H)为库面积均值函数；Wn(t)为随机数学中的维纳过程。通过对上述公式方程的求解计算，便可以得到在临界模式下的漫坝风险值。

2.2 临界模式

在水库工程中，通常情况下，存在两种临界模式，其1为坝顶高程，其2为防浪墙高程，在研究的水库中，取相应的坝顶高程112 m与防浪墙高程为113 m，并且二者之间相对应的风险分别为R1与R2，则对应的作用计算公式为：

g(*)=112-Z-e

g(*)=113-Z-e-Rp

2.3 计算结果与分析

本文研究的水库的相应校核标准为2000年，对此，在研究中，针对在不同的迎汛水位的条件下，对上限的洪水系列与有效风系列联合作用下的漫坝风险进行了慢板风险的计算。通过计算得到的计算结果如下：

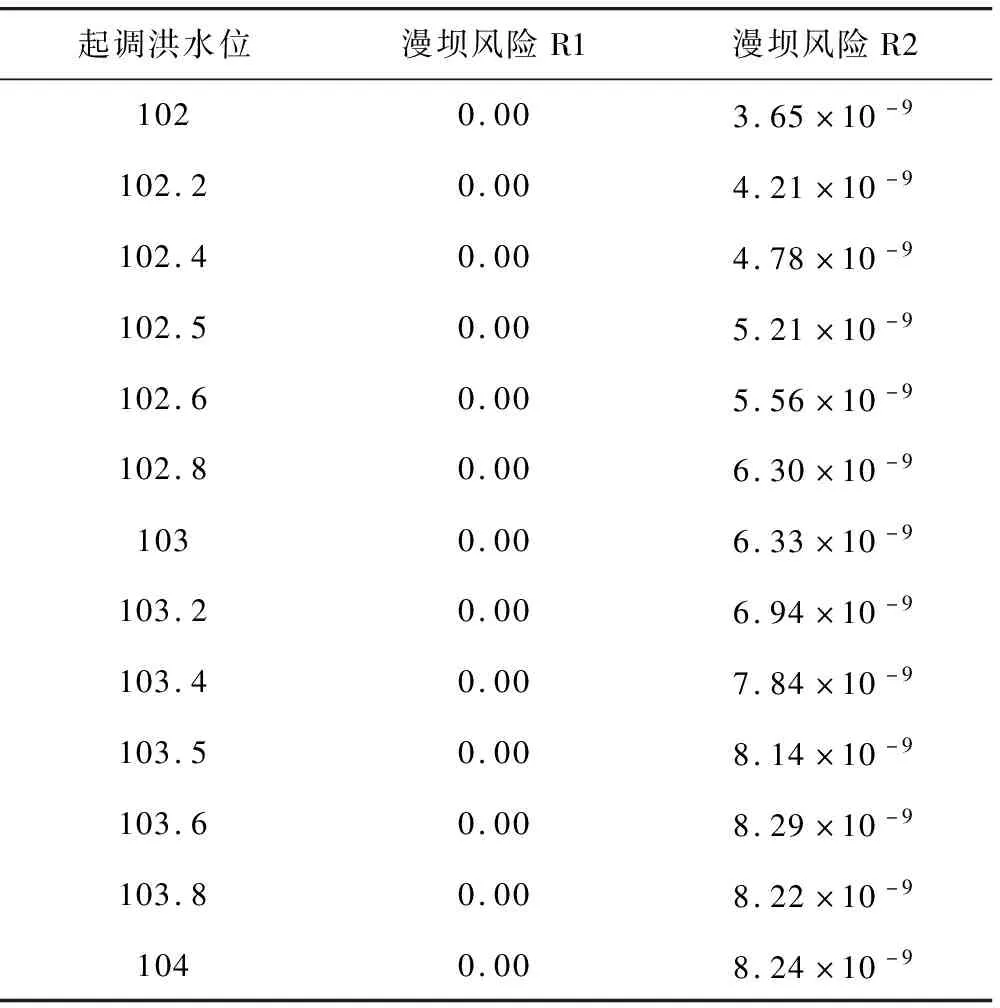
表1 水库漫坝风险计算结果

通过表2分析可知，汛线水位从102.0 m变化到104.0 m的过程中，漫坝风险的概率一直处于10-9数量级,可靠度十分高，对于工程管理而言是完全可以接受的。

3 结语

伴随着科学技术水平的不断提高，漫坝风险分析模型成为实际水利工程中分析缺水水库的防洪与性利之间的矛盾的理论基础。本文在分析漫坝理论的基础上，建立新疆某水库大坝在洪水系列与风浪系列联合作用下的漫坝风险模型，并通过计算，该水库的漫坝风险可能性处于10-9数量级，完全符合工程管理要求。通过分析可知，通过在实际工程中应用漫坝分析理论，可以有效的为管理人员提供参考，从而为整个工程创造效益。