新疆荒漠区水文序列演变分析及变异点诊断

王 新

(新疆水文局水文实验站，新疆 乌鲁木齐 830000)

生态水文演变规律和过程模拟研究是生态水文学研究的重要内容之一。在生态水文学研究中，未来的发展趋势主要包括三个方面，即流域生态水文机理研究、流域生态水文模型研究和流域植被生态水文过程演变规律的研究[1]。为了解决植被条件“稳态不变”的假设对水文模型的限制，流域生态水文模型是在水文模型中引入作物生长模型或者陆面过程模型，发展生态水文耦合模型[2]。流域生态水文模型研究的核心内容就是建立尺度匹配的生态过程和水文过程的耦合机制和模拟方法，这是生态水文微观机理走向宏观应用的重要阶段[3]。植被动力学方程是生态学中描述植被演化过程的重要方法之一，将其引入生态水文演化模型将推动生态水文模型研究的发展。新疆荒漠区生态水文系统演化规律的研究对于旱区生态水文学的研究具有重要的科学意义，可为新疆荒漠区生态环境的保护提供理论支撑[4]。

本文主要对降水的日数演变规律和降水量的演变规律进行计算分析，对水文序列的持续性、趋势性和周期进行分析，对水文序列的变异点进行诊断。

1 荒漠区概况及基本统计特征

1.1 荒漠区概况

本文选取的研究区典型站点位置如图1所示，位于新疆荒漠区的核心地带，土地利用类型为荒地，具有一定的代表性，研究区为该点为中心的15 km内区域，面积812 km2，新疆荒漠区属暖温带和温带半干旱大陆性季风气候，年降水基本在385 mm左右波动，降水主要集中在5-8月，最大降水量可达到600～800 mm左右，最小降水量100～150 mm左右。年蒸发量比较大，年蒸发量1 300 mm左右，最小值980 mm左右，最大值接近1 450 mm。年平均气温9.3℃。最高10.1℃，最低8.2℃。一年中气温1月份最低，平均-10.3℃，七月份最高平均24.5℃，年较差34.8℃。春、夏、秋、冬平均气温分别是9.4℃、21.7℃、8.9℃、-8.1℃。其中，春季温度上升和秋季温度下降速度快。

图1 研究区区域

1.2 基本水文资料

水文资料是水文分析计算的基础，本文的降水与蒸发资料均取自A气象站。降水资料新疆荒漠区A气象站年降水变化如图2所示，年降水序列从1951-2013年，多年平均降水为398 mm，年降水基本在多年平均值附近波动。新疆荒漠区A气象站年蒸发序列从1951-2010年，年际变化较大，最大值出现在2006年为1 542.3 mm，最小值出现在1952年为1 022 mm。年降水日数持续性和趋势性分析对新疆荒漠区A测站降水日数、降水量大于等于5 mm的日数以及降水量大于等于10 mm的日数用R/S分析法进行持续性计算检验，所得结果见表1所示。降水日数H值介于0.5和1之间，表现为正持续性，U值为负值，且绝对值大于1.96，说明新疆荒漠区降水日数在未来呈现显著的递减趋势，且具有正持续性；降水量大于等于5 mm的日数H值介于0.5和1之间，表现为正持续性，U值为负值，且绝对值小于1.96。说明新疆荒漠区降水量大于等于5 mm的日数在未来呈现不显著的递减趋势，且具有正持续性；降水量大于等于10 mm的日数H值介于0.5和1之间，表现为正持续性，U值为负值，且绝对值小于1.96。说明新疆荒漠区降水量大于等于10 mm的日数在未来呈现不显著的递减趋势，且具有正持续性(见表1)。

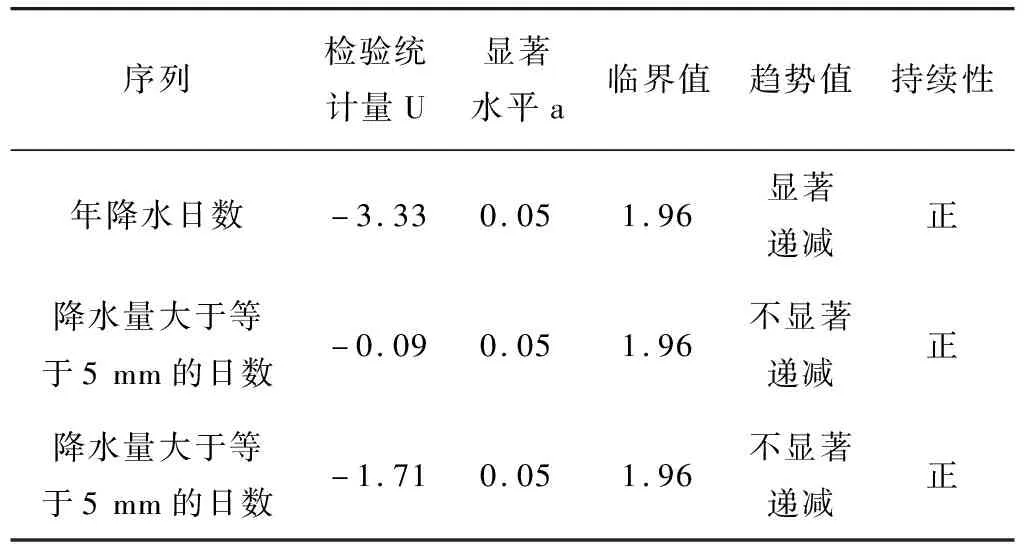
表1 各年有降水日数趋势统计表

1.3 年最大降水日数持续性和趋势性分析

对新疆荒漠区A测站最大日降水量用R/S分析法和Kendall秩次相关检验法进行持续性和趋势性的计算检验，所得结果如表2所示。H值介于0.5和1之间，表现为正持续性，U值为正值，且绝对值小于1.96，说明新疆荒漠区最大日降水量在未来呈现不显著的递增趋势，且具有负持续性。

表2 趋势统计表

1.4 年降水大于5 mm和10 mm日数持续性和趋势性分析

对新疆荒漠区A测站大于5 mm和10 mm累计降水量用R/S分析法和Kendall秩次相关检验法进行持续性和趋势性的计算检验，所得结果如表3所示。分析计算可知，A测站大于5 mm累计降水量H值介于0.5和1之间，表现为正持续性，U值为负值，且绝对值小于1.96。说明新疆荒漠区大于5 mm累计降水量在未来呈现不显著的递减趋势，且具有正持续性。A测站大于10 mm累计降水量H值介于0.5和1之间，表现为正持续性，U值为负值，且绝对值小于1.96。说明新疆荒漠区大于5 mm累计降水量在未来呈现不显著的递减趋势，且具有正持续性。

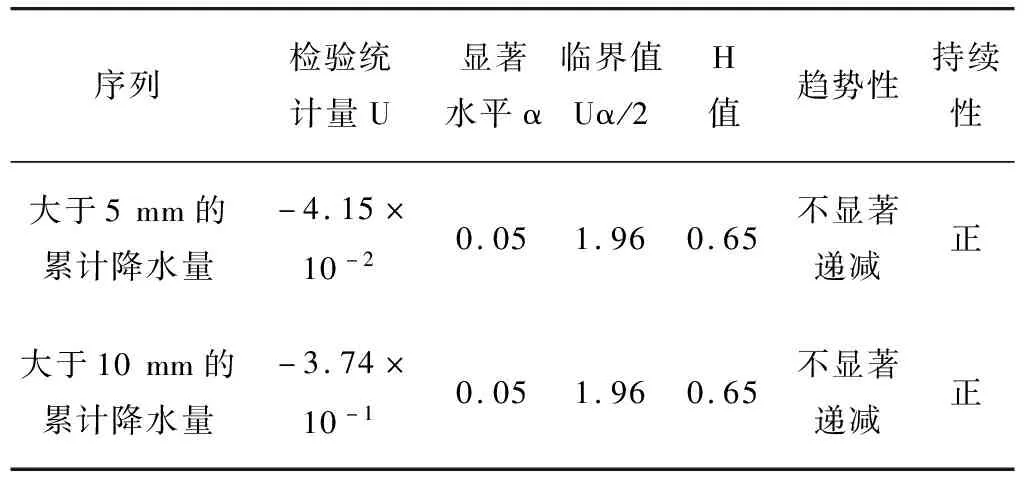
表3 趋势表

1.5 水文序列演变周期性分析

对新疆荒漠区A测站的降水大于5 mm日数和降水大于5 mm日数用小波分析法进行周期性分析，如图2所示。降水大于5 mm日数序列小波方差有2个峰值，分别对应21年和36 a的时间尺度，第一峰值为36 a。说明年降水序列36年的周期振荡最强烈，为第1主周期，第2主周期为21 a；同理，降水大于10 mm日数序列小波方差也有2个峰值，也分别对应21 a和36 a的时间尺度。

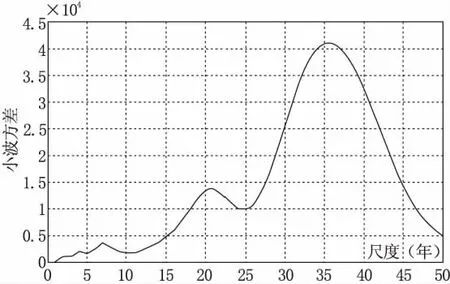
图2 降水大于5 mm日数序列小波变换方差图

应用R/S分析法对年降水日数、年最大降水日、年降水大于5 mm和10 mm的日数进行趋势性和持续性分析，得到结果如表4所示。

表4 水文序列演变持续性和趋势性统计表

2 水文序列变异点诊断

应用Mann-Kendall统计检验法对新疆荒漠区A站1951-2013年降水序列进行突变分析，判断出变异点所在位置，同时运用累积距平法进行检验和补充得到最终诊断结果。

2.1 Mann-Kendall法

Mann和Kendall最先提出并应用Mann-Kendall检验进行非参数检验方法，现已广泛的使用。Mann-Kendall方法分析了水文序列变化的趋势，最大优点是不仅能够使样本不必服从特定分布，同时可以受少数异常值干扰，适用于水文等这类非正态分布数据[5]。

2.2 累积距平法

距平是最常用的表示变量偏离正常情况的量，一组数据的某一个数与均值之间的差就是距平，即变量的一组数据与其均值的差异就构成了距平序列[6]。

2.3 年降水和蒸发序列变异点诊断

对年降水和蒸发序列，采用Mann-Kendall法和累积距平法结果对比分析，结果如图3和图4所示。由图3可以看出，UF和UB两条曲线相较于1958年、1964年和1969年，由图4可以看出，累积距平曲线在1969年附近出现转折，故年降水的变异点在1969年。

图3 降水变异

图4 降水累积距平曲线分析

采用Mann-Kendall法和累积距平法结果对比分析，如图5和图6所示。由图5可以看出，UF和UB两条曲线相较于1998年，由图6可以看出，累积距平曲线在1966年附近出现转折，故年蒸发的变异点在1966年和1998年。

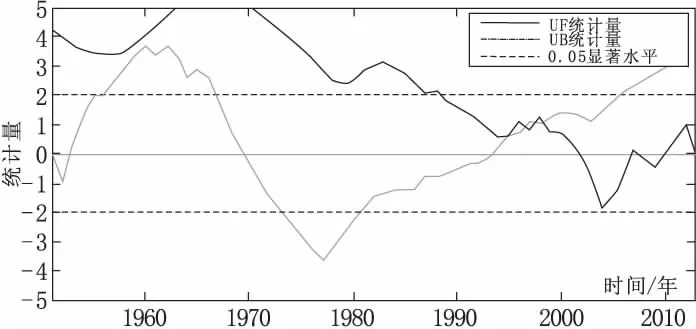
图5 蒸发变异

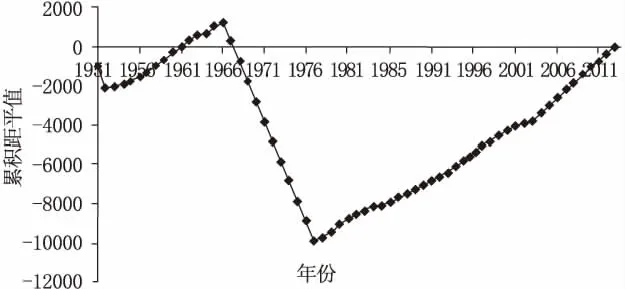
图6 蒸发累积距平曲线分析

2.4 年降水日数变异点诊断

对年降水日数序列采用Mann-Kendall法和累积距平法进行计算分析，结果如图7和图8所示。由图7可以看出，UF和UB两条曲线相较于1979年，由图8可以看出，累积距平曲线在1979年附近出现转折，故年降水日数的变异点在1979年。

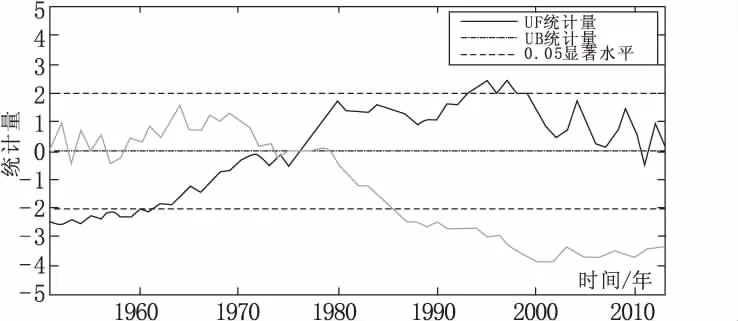
图7 年降水日数变异

图8 有降水的日数累积距平曲线分析

用Mann-Kendall法与累积距平法对降水量和蒸发量序列以及年降水日数进行变异点诊断，得到结果如表5所示：

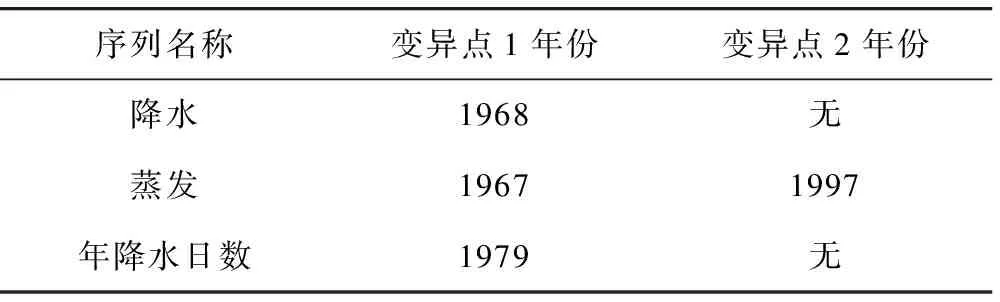
表5 水文序列变异点统计表

3 结语

通过本文研究，可以得到以下结论：

(1)各年最大日降水量1951年最大，为141.7 mm，最小发生在1966年56.2 mm；最大降水日主要集中在7-9月，与降水量集中时间基本一致，7-9月最大降水日占到全年的88%。

(2)月降水日数均呈下降趋势，其中7到9月呈显著的下降趋势；3、4、6、10和11月日降水大于5 mm的日数均呈下降趋势，6、8和9月呈上升趋势，7月在一个稳定值附近波动；5、6、7和8月日降水大于10 mm的日数均在一个稳定值附近波动，而10月呈下降局势。

(3)应用R/S分析法对年降水日数、年最大降水日、年降水大于5 mm和 10 mm的日数进行趋势性和持续性分析，年降水日数显著递减，其余都不显著。

(4)用Mann-Kendall法与累积距平法对降水量和蒸发量序列以及年降水日数进行变异点诊断，年降水日数的变异点在1979年。