基于AHP的阿拉尔市水资源系统评价研究

刘熙娟，于德珠，刘 云

(塔里木大学信息工程学院，新疆 阿拉尔 843300)

水资源是人类生存与社会经济发展的基础物资保障，是无法替代的自然资源。干旱地区社会经济的发展受制于水资源尤为突出，在水资源量一定的情况下，随着区域内人口的增加、经济的发展以及农业种植面积的扩大，用水需求量不断增大，加剧了水资源的供需矛盾。因此，当人类开发利用水资源时，必须按照水循环规律，合理利用水资源[1]。近年来，许多学者对水资源相关问题进行了大量卓有成效的研究，何钰等[2]采用BP神经网络模型和综合指数评价法对嘉陵江南充段干流的水质进行了评价。杨子江等[3]，Changhai Wang等[4]，张斌等[5]利用系统动力学的方法分析了水资源承载力问题。Xijuan Liu等[6]利用系统动力学SD研究了阿拉尔市水资源承载能力。牛旭等[7]运用可拓层次分析法，研究了阿拉尔市水资源可持续发展问题。许丽[8]利用灰色系统模型分析了农业水资源供需平衡。刘昭阳[9]结合当地水资源自然赋存条件、开发利用现状及其可持续利用发展要求，利用AHP层次分析法对庄河市水资源现状进行了科学评价。艾亚迪等[10]应用AHP对西安市水资源开发利用状况进行了Arcgis可视化分析。安强等[11]通过构建模糊综合评价模型，综合评价分析了河南省中原城市群水资源承载力水平。陈海涛等[12]基于熵权模糊综合评价模型，对河南省近10年的水资源承载力展开了评价。综上所述，前人关于水资源相关问题的研究可谓是硕果累累，为后续学者的研究提供了参考和经验。本文参照前人研究成果，综合利用层次分析法AHP和模糊综合评价法FCE，选取影响水资源的相关客观因素为评价指标，建立判断矩阵，计算各指标权重，得到各指标的综合评分，进而获得客观因素对评价指标权重的影响。这对阿拉尔市人口、环境、经济、社会与水资源协调可持续发展有着重要的意义。

1 研究区现状

新疆生产建设兵团第一师阿拉尔市，北起天山南麓山地，南至塔克拉玛干沙漠边缘，东临沙雅县，西抵柯坪县，师市总面积693 968 hm2，其中阿拉尔市面积625 668 hm2。由塔里木的阿拉尔、沙井子2大垦区和四、五、六团3个独立垦区组成。第一师阿拉尔市属暖温带极端大陆性干旱荒漠气候，垦区平均气温10.8℃，极端最高气温35℃(沙井子垦区每隔5～10 a遇最高气温40℃)，极端最低气温-28℃(四团垦区最低气温为-33.2℃)。垦区长年气候干燥、雨量稀少，冬季少雪，地表蒸发强烈，年均降水量为40.1～82.5 mm，年均蒸发量1 876.6～2 558.9 mm。

阿克苏河、和田河、叶尔羌河在阿拉尔市交汇形成塔里木河,区域土壤由塔里木河冲积而成。市区处于塔里木河冲积平原二级阶梯上，为地下水径流排泄区，地下水埋深1.4～1.7 m，最低水位出现在1-2月，地下水位年度变化幅度为0.5～1.0 m。地下水径流缓慢，流速为 0.02～0.05 m/昼夜，地下水流向自西向东，其水力坡度为0.04%～0.06%，地下水类型为河谷性冲积层潜水，地下水类型为硫酸盐类水，矿度很高一般在1～5 g/L：普遍在3 g/L，局部高达10 g/L。

阿拉尔垦区紧邻塔克拉玛干沙漠，气候极为干旱，水资源承载力薄弱。随着垦区内土地耕种面积的不断扩大以及新疆生产建设兵团在这里建市带来人口的激增，使得垦区内水资源供需矛盾日益突出，严重影响着这一地区农业生产及社会经济的发展。因此，合理开发利用水资源已成为阿拉尔市急需解决的问题之一。

2 评价方法

2.1 层次分析法AHP的应用

层次分析法[9,10,13,14](Analytic Hierarchy Process，简称AHP)是将与决策有关的元素分解成目标、准则、方案等层次，在此基础上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，提出的一种层次权重决策分析方法。层次分析法将复杂的决策系统层次化，通过逐层比较各种关联因素的重要性来分析、决策提供定量的依据。

2.1.1 数据分层

从水资源的生态、社会、经济效益这三个准则出发，分别选取若干能反应这三大效能的指标，建立水资源评价指标体系，见表1。

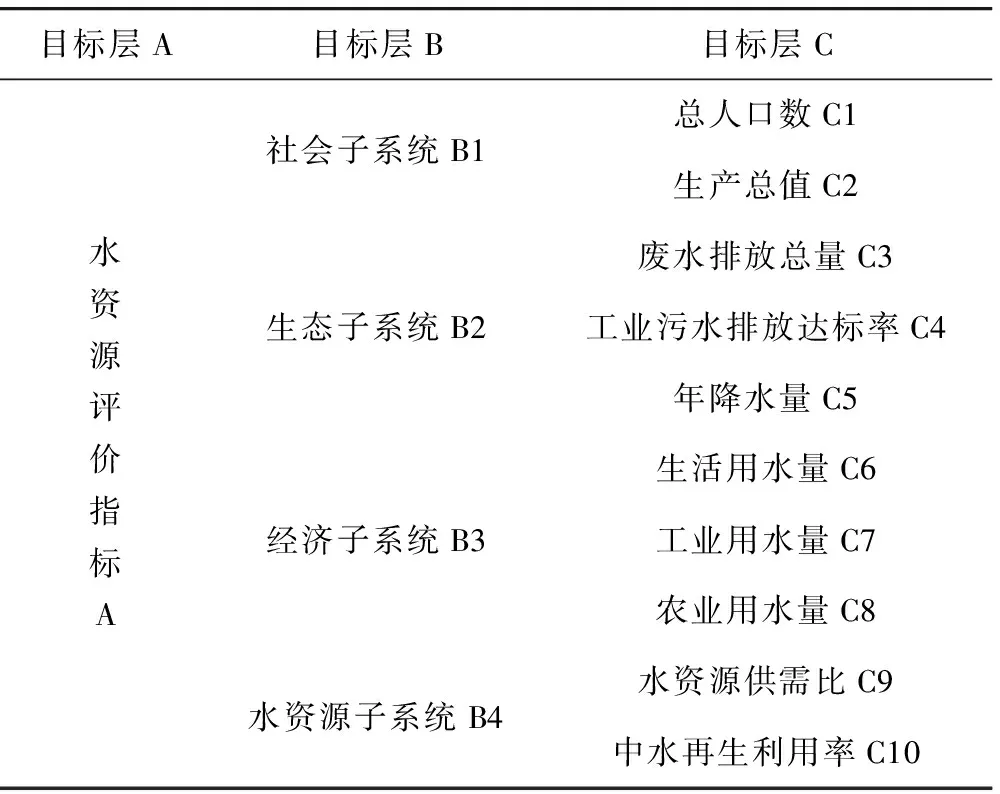
表1 水资源评价指标体系

2.1.2 层次分析法

1)水资源评价指标权重的确定

采用Santy的1-9标度方法[9，10]构建判断矩阵，计算各指标权重，并对其进行一致性检验。以水资源评价指标体系中的目标层B的4个指标为例，构建水资源效益A-B判断矩阵并进行一致性检验。

(1)构建判断矩阵P，见表2。

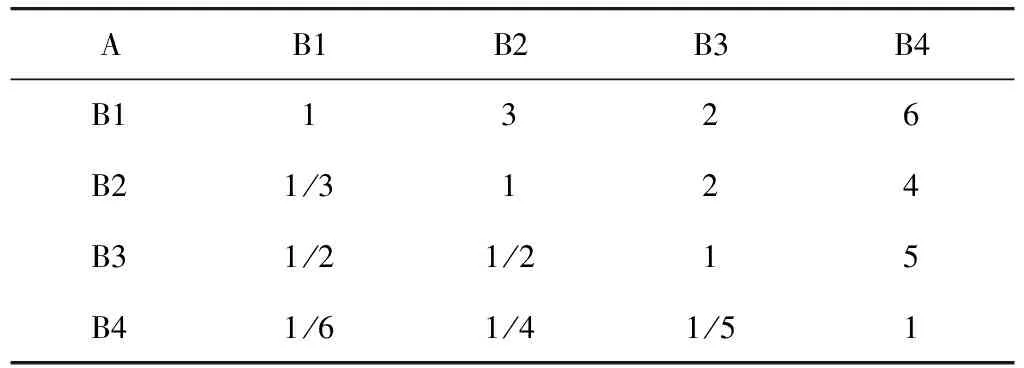
表2 A-B判断矩阵

(2)计算权重。

应用层次分析法计算权重的方法有很多，这里选取准确率比较高的方法——取列向量的算术平均[9,10]，计算矩阵对应的权重，得到如下结果：

W0=(0.480 4，0.254 2，0.207 2，0.058 2)

(3)一致性检验。

为了判断上述权重值的合理性，需要进行一致性检验，具体过程如下所示：

计算矩阵的最大特征值

PW0=λmaxW0⟹λmax=4.177 4

进行一致性检验：根据下列公式进行一致性检验

式中：n为元素个数，RI(Random Index)为平均随机一致性指标，取值可参考文献[9，10]。可求得CI0=0.059 1，CR0=0.065 7<0.1，满足一致性检验要求，说明各层次权重值可用于水资源评价。

2)子系统单个指标权重的确定

根据上述方法，可以计算目标层C中的10个指标的权重，并进行一致性检验，结果见表3～表6。

表3 B1-C判断矩阵

表4 B2-C判断矩阵

从表3～表6可以看出，文中选取的所有指标都满足一致性检验要求，所确定的各层次的权重值具有一定的科学性。因而可以选取上述表中计算得出的权重进行后续的计算。

表5 B3-C判断矩阵

表6 B4-C判断矩阵

2.2 模糊综合评价法FCE的应用

水资源承载力评价系统受自然、社会等多因素的综合影响，具有随机性、模糊性等特点，模糊综合评价法[12,13](Fuzzy Comprehensive Evaluation，简称FCE)可以较好实现对水资源承载力进行多层次、多目标的综合评价。模糊综合评价法中评价因子主要是由隶属度矩阵(评判矩阵)、因素集、评判集所构成。进行模糊综合评价通常按以下步骤进行：

1)确定因素集：U={U1，U2，U3，…，Uk}(k=1，2，3，…)；

2)确定评判集：V={V1，V2，V3，…，Vk}(k=1，2，3，…)；

3)进行单因素评判得：ri={ri1，Vi2，Vi3，…，Vik}(k=1，2，3，…)；

4)构造综合评判矩阵R；

5)综合评判：结合层次分析法获得的权重W，计算模糊综合评价结果E，其中E=W×R。

3 结果分析

本文的数据来源于2008-2017年《新疆兵团第一师阿拉尔市统计年鉴》和知网数据平台。将层次分析法和模糊综合评价法结合，可以消除AHP中主观因素的影响，也可以克服多层次评价的不足。本研究在层次分析法的基础上使用模糊综合评价法，根据社会、生态、经济、水资源子系统，将数据分成4部分。以社会子系统为例，计算水资源综合评价结果。原始数据如表7所示。

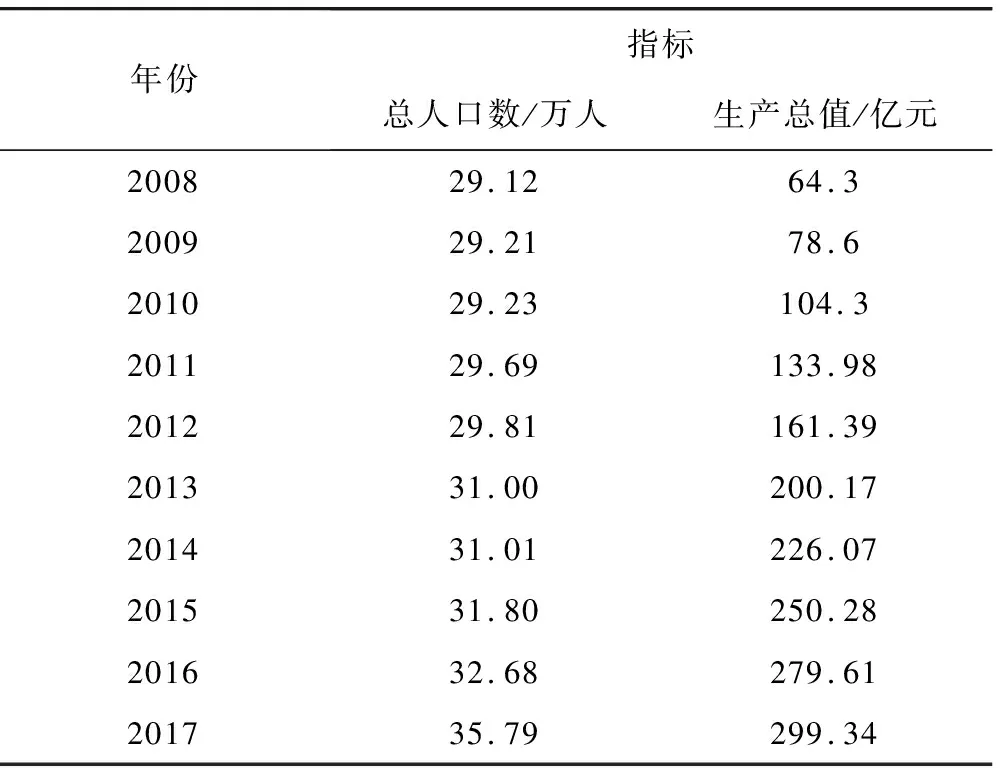
表7 社会子系统相关指标原始数据

使用FCE得到综合评价结果E。详细过程如下：

标准化数据。将表7中每年的数据使用归一化方法标准化，结果如表8所示：

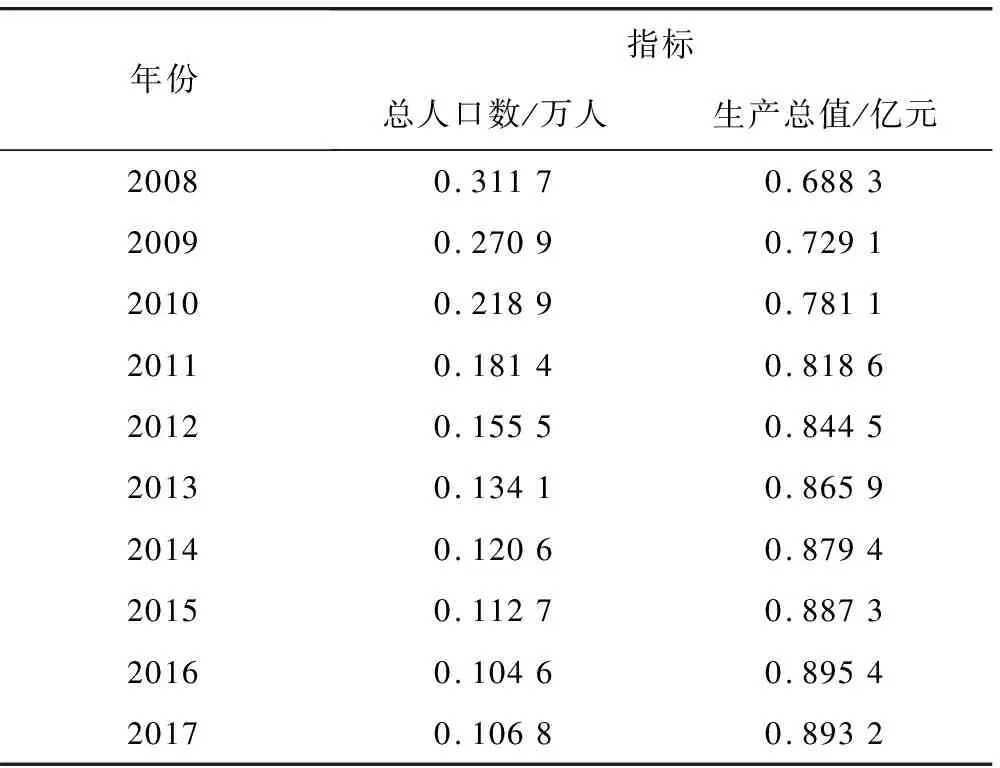
表8 标准化后的数据

2)确定评判矩阵。将表8中的数据处理后，可得到因素集的评判矩阵如下。

3)计算综合隶属度。计算权重和评判矩阵的乘积，可得到评价结果。

EB1=W1×RB1=(0.750 0 0.250 0)×

=(0.405 8 0.385 4 0.359 5 0.340 7 0.327 7 0.317 1 0.310 3 0.306 4 0.302 3 0.303 4)

对于其他3个子系统，可使用同样的方法，得到B2, B3, B4对应的因素集评判矩阵，分别如下所示：

这3个子系统的权重分别为

W2=(0.549 9, 0.240 2, 0.209 8),W3=(0.486 9, 0.435 3, 0.077 8),W4=(0.857 1, 0.142 9)

计算得其他3个子系统的评价结果EB2，EB3，EB4如下

EB2=(0.476 4 0.498 6 0.512 9 0.521 0 0.488 6 0.474 1 0.535 1 0.532 7 0.534 0 0.533 0)

EB3=(0.081 8 0.082 0 0.082 7 0.083 1 0.082 9 0.083 0 0.082 7 0.083 8 0.081 9 0.081 9)

EB4=(0.797 6 0.777 8 0.759 7 0.701 0 0.672 8 0.626 3 0.604 5 0.591 1 0.568 6 0.539 4)

4)计算综合评价结果。根据以上分析计算因子集的综合评价结果，可用下式表示：

UE={UB1，UB2，UB3，UB4}

由此，可以得到综合评价指标数据，如表9所示。

表9 综合评价指标数据

考虑到生态子系统和经济子系统对水资源评价有负向影响，故水资源评价指标实际权重为

WE=(0.445 5 -0.273 8 -0.219 3 0.061 4)

所以，水资源综合评判结果为

E=WE×RE=(0.058 7 0.049 7 0.040 5 0.033 3 0.035 1 0.034 0 0.020 3 0.019 0 0.017 2 0.016 9)

为了更好地预测未来水资源发展状况，对水资源综合评分进行线性拟合和二次拟合，以便更好地观测水资源安全问题随着年份的增加所呈现的趋势。所得结果如图1和图2所示。

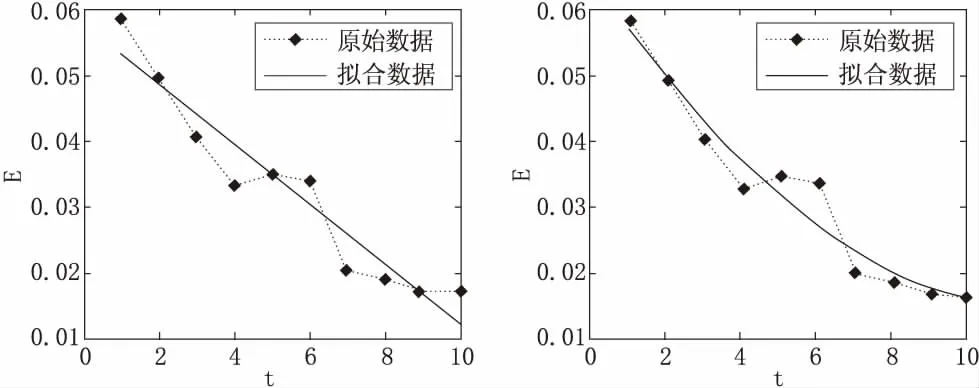
图1 线性拟合 图2 二次拟合

将表9数据标准化后得到隶属度矩阵

图中横轴t代表第几年，比如1代表所选取数据的第1年即2008年，10为第10年即2017年。纵轴为综合评分E。由图1可以得到综合评分E和时间t对应的拟合函数为

E=-0.004 6t+0.057 5

根据上述表达式，可以得到未来10年(2018-2027)的预测结果：0.006 9 0.002 3 -0.002 3 -0.006 9 -0.011 5 -0.016 1 -0.020 7 -0.025 3 -0.029 9 -0.034 5。

根据模糊综合评价方法的结果分析[12,13]，模糊结果E的值越大，表明当地的水安全性就越高，也就是说，E值越大，表明该地区越不会出现水危机现象。

显然，根据预测结果，2020年将出现水资源短缺情况。也就是说，这一年阿拉尔市水资源的供给远远赶不上水资源的需求，这种形势在未来可能会越来越严重。如果未来10年，没有特别的水资源供给，阿拉尔市的可用水资源将会缺乏，这将对当地的经济发展和人民的生活带来很大的压力。随着阿拉尔市社会经济的不断发展，需要引进外来水的供给，加大水资源重复利用，才能实现当地水资源可持续开发利用，解决日益突出的水资源供需矛盾。

4 结语

本文利用层次分析法构建了阿拉尔市水资源评价指标体系的层次模型，建立了判断矩阵，对所获得的指标权重进行了一致性检验，使得各层指标权重有效，并用模糊综合评价方法获得了各个指标的综合评价结果。将AHP和FCE相结合进行讨论，提高了评价结果的真实性和有效性，克服了AHP专家评分法主观性太强的不足。研究结果表明，当前水资源使用不合理，阿拉尔市将会出现水危机现象。因而根据当地实际情况，积极推进节水型城市的建设，提高工业用水重复利用率，同时提高水资源的系统管理水平，加强水源地保护，严格控制取用水量；建议开发利用中水、微咸水等非常规水源，淘汰高耗水企业，引进外来水的供给，合理开发利用水资源，加强对生态环境的保护，努力打造人与自然和谐相处的局面。