城市轨道交通网络首班车时段时刻表优化研究
杨冀琴,田 秦,徐占东,雷 莉
(1. 成都工业职业技术学院,四川 成都 610218;2.西南交通大学 交通运输与物流学院,四川 成都 611756;3. 中国铁路成都局集团有限公司干部培训中心,四川 成都 611731)
0 引 言
随着城市轨道交通网络的形成,其一方面为居民的出行带来便捷,另一方面网络的复杂性给列车换乘衔接问题增加了难度。由于各条线路根据其客流情况确定一天的运营时间,各线路的运营时间不同。因此,根据首末班车的客流特性制定适宜的时刻表,提供高效的列车衔接优化方案,对于提高乘客换乘效率,提升城市轨道交通早晚间运营服务水平具有一定的理论与现实意义。
近年来,末班车的换乘衔接优化引起了研究者的关注,主要集中在以下几个方面:①基于线网的可达性优化末班车时刻表[1,2];②采用分层协调策略[3],开展网络换乘衔接优化研究;③基于全网衔接优化,构建网络末班车衔接和时刻表的优化模型,考虑不同的优化目标:乘客换乘衔接间隔最大[4]、换乘冗余时间的标准差最小[5]、乘客总换乘等车时间最小化[6]、换乘衔接的客流量最大[7]、成功换乘衔接客流量最大和总换乘等车时间最小[8]、最大限度满足旅客需求[9]、减少乘客换乘等车时间与乘客不可达OD量和改善可达乘客的可靠性[10]、换乘成功乘客数量最大和末班车运行时间最小[11]。
在首班车的衔接优化方面,基于换乘衔接方向的重要程度,徐瑞华等[3]设计分层协调的优化策略和算法;宋悦等[12]提出将各个换乘方向的换乘客流量作为权重定量衡量首班车协调层次的方法;W. L. ZHOU等[10]以乘客总的起点等车和换乘等车时间最短为目标;L. J. KANG等[13]以总的乘客换乘等车时间最小、列车到站时间差最小、在合理的时间内未实现换乘服务的列车数量最小[14]为目标;X. GUO等[15]提出子网络衔接方法,使首班车列车间的衔接时间最小,分别采用遗传算法[10, 12]、模拟退火算法[13]、启发式搜索算法[14]和CPLEX软件[15]进行求解。
当前研究主要集中于末班车的换乘衔接,对首班车的换乘衔接研究较少,已有研究未考虑企业运营成本。然而,首班车的乘客行为和客流特征与末班车不同,换乘衔接的目标也不同。考虑到首班车时段的客流需求较少、运能充足等特点,笔者以乘客换乘等车成本和线路发车成本最小为优化目标,构建首班车时段列车时刻表优化模型,利用遗传算法进行求解。
1 首班车时段换乘衔接优化问题概述
首班车时段的运营组织是城市轨道交通全天运营的基础,该时段的时刻表是全天运营时刻表的一部分。笔者提出的首班车时段不是指各条线路每日早间运营发出的首班列车,而是指从各条线路首班车出发开始到早高峰之前或者到早高峰时段内的某个时间为止。该时段的选取与各个城市的最早发车时间、线路运行时间和客流高峰时段有关,例如,从运营公司最早发车时间开始至早高峰时段之前(6:30—8:00)。
首班车时段由于接近早高峰时段,客流量较少但呈逐渐增加的趋势。首班车时段的乘客不存在换乘不可达情况,仅有乘客换乘等车时间的长短之分。如图1,乘客从L线路上的第q班列车换乘到L′线路的第q′班列车上,此时换乘等车时间大于等于0,换乘等车时间取决于换乘列车间的衔接时间与乘客的换乘走行时间。如果列车的衔接时间不合理,导致乘客在换乘站等车时间过长,会降低乘客的满意度和轨道交通的运营服务水平。

图1 首班车时段乘客换乘衔接过程Fig. 1 Passenger transfer connection at the first train time period
2 城市轨道交通线网拓扑图的简化
城市轨道交通线网由若干条线路组成,各条线路由若干个车站与区间构成。因此,线网可用所有车站与区间共同组成的拓扑来表示。车站按照其在线路中的具体位置可以分为中间站、换乘站、端点站(起点站和终点站)3种,见图2。

图2 城市轨道交通线网拓扑Fig. 2 Network topology of urban rail transit
随着线网规模的扩大,线网中线路和车站随之增加,适当简化线网拓扑,可以方便模型求解并提高模型对大规模网络的适用性。由于端点站的发车时间和换乘站的到站、离站时间对换乘衔接影响较大,称其为关键站;其余的中间站称为非关键站。因此,将端点站与换乘站间以及相邻换乘站间的列车运行区间进行简化,得到由端点站、换乘站以及区段组成的轨道交通线网简化拓扑(图3)。
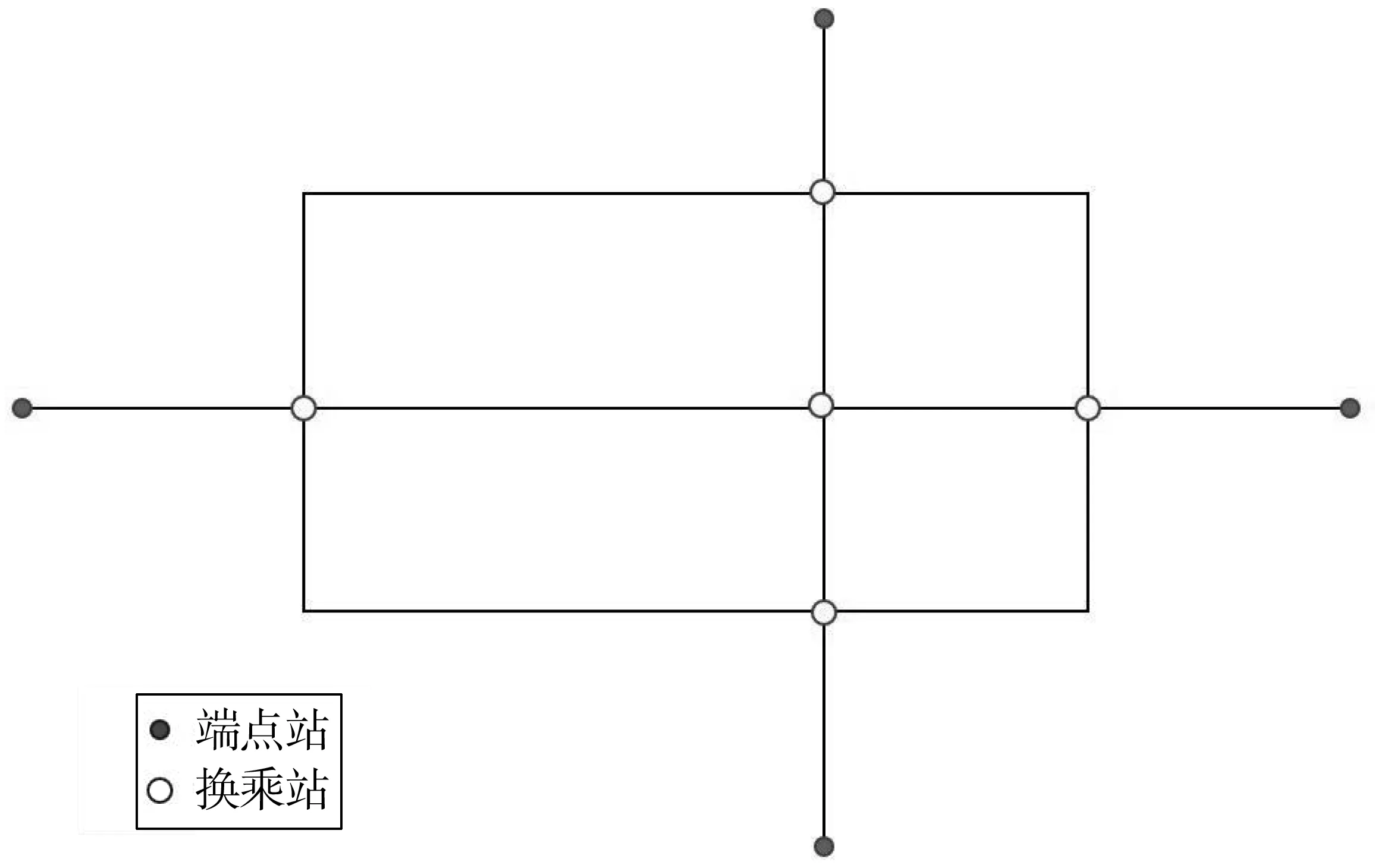
图3 城市轨道交通线网简化拓扑Fig. 3 Simplified network topology of urban rail transit
便于问题描述,对线网模型的基础参数做如下定义:I为线网中线路的集合, 任意一条线路分上、下行储存在集合中,I={i|i=1,2,3,…,LI},其中LI为集合中线路的数量;X为线网中关键站的集合,X={x|x=1,2,3,…,SX},其中SX为集合中关键站的数量;Q为线网中所有线路的列车班次序号集合,Q={q|q=1,2,3,…,NQ}, 其中NQ为时段内所有线路的最大发车班次。
3 首班车时段时刻表优化模型构建
首班车时段内由于有后续列车的衔接,乘客的可达性可以得到保证,但列车之间衔接时间过长,会造成乘客的换乘不便。由于首班车时段客流较少,线网运力较充足,因此,除了考虑线路的衔接关系以减少乘客的换乘等车时间,该时段的衔接优化目标还可兼顾企业的运营成本。笔者考虑乘客和运营两个方面,以乘客换乘等车成本和线路发车成本最小为目标,构建首班车时段的列车时刻表优化模型。
3.1 模型假设
1)同一个换乘站不同乘客的换乘走行时间相同。首班车时段乘客的出行特征区别较小,走行时间比较接近。
2)各线路首班列车的发车时间不早于运营公司设定的最早发车时间。
3)假设首班车时段的列车运载能力充足,乘客不会因列车满载而被滞留在车站,即乘客在起点站与换乘站均乘坐乘客到站后的第一列到达车站的列车。
3.2 优化目标
为了提高乘客换乘方便性,并减少城市轨道交通的运营成本,笔者构建的首班车时段列车时刻表优化模型的目标函数为总成本(乘客换乘等车时间成本和企业运营发车成本)最小,考虑乘客的换乘走行时间和换乘失败惩罚,以列车离开、到达关键站时间、区间运行时间以及关键站停站时间为决策变量。
3.2.1 换乘等车时间成本
乘客换乘衔接时间为线路j衔接列车的第q’班列车从换乘站x的出发时间(D′xjq)减去线路i换乘列车第q班列车到达换乘站x的时间(Axiq)与乘客在换乘站x从线路i到线路j的换乘走行时间Tij,w之和。从线路i的第q班列车换乘到线路j的第q′班列车的乘客换乘等车时间Wijqq′为:
Wijqq′=Dxjq′-Axiq-Tij,w
(1)
与末班车不同,首班车时段乘客不会出现换乘失败不可达的情况,但是可能出现换乘等待时间过长的情况。笔者将乘客能够忍受的最大换乘等车时间(Tij,C)作为首班车时段换乘失败与否的判别标准。如果乘客的换乘等车时间小于等于Tij,C,则根据式(1)可得出乘客的换乘等车时间。如果乘客的换乘等车时间大于Tij,C,将这种情况视为“换乘失败”,笔者引入换乘惩罚值,乘客的换乘等车时间为:
Wijqq′=max{Dxjq′-Axiq-Tij,w,εij}
(2)
式中:εij为从线路i到线路j换乘失败后的惩罚值。
换乘等车时间通过时间费用转换系数δ转换得到换乘等车时间成本。换乘等车时间成本为首班车时段内线网中所有换乘乘客的换乘等车时间成本之和:
(3)
式中:Ni,u为线路i首班车时段内的发车数量;Cijq为从线路i上的第q班列车换乘到线路j的乘客数量。
3.2.2 发车成本
发车成本为线网中所有线路在首班车时段内发出的列车所产生的运营成本之和:
(4)
式中:Gi为线路i每发出一列车的发车成本,笔者主要考虑电力成本。
3.2.3 目标函数
换乘等车时间成本和发车成本之和是首班车时段时刻表优化模型的目标函数,如式(5):
(5)
3.3 约束条件
3.3.1 模型变量的基础关系
列车到达某关键站的时间可用该线路起点站的离站时间、区间运行时间以及关键站停站时间来表示,如式(6):
(6)
式中:Rxiq为线路i上的第q班列车从关键站x-1行驶到关键站x的区间运行时间,包括所经过的非关键站的停站时间;Pxiq为线路i上的第q班列车在关键站x的停站时间。
同理,列车离开某关键站的时间可表述为:
(7)
由式(6)、式(7)可以得出列车离开某关键站的时间Dxiq等于到达该站的时间Axiq与该站的停站时间Pxiq之和,如式(8):
Dxiq=Axiq+Pxiq
(8)
3.3.2 乘客换乘成功等车时间约束
考虑到在首班车时段客流量较少、运能充足的情况下,没有乘客滞留的现象,乘客在换乘站乘坐乘客到站后的第一列到达车站的衔接列车,即为乘客换乘成功。乘客的换乘成功等车时间应该满足以下约束条件:
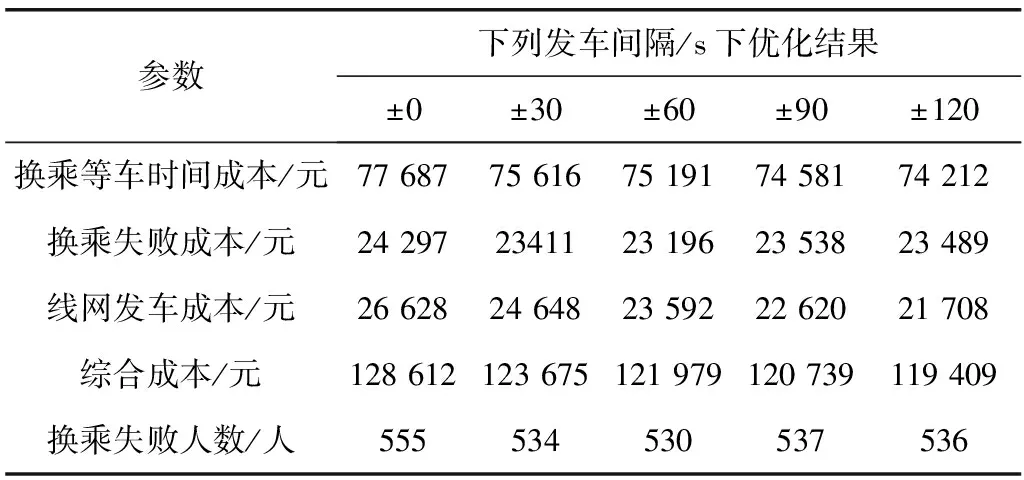
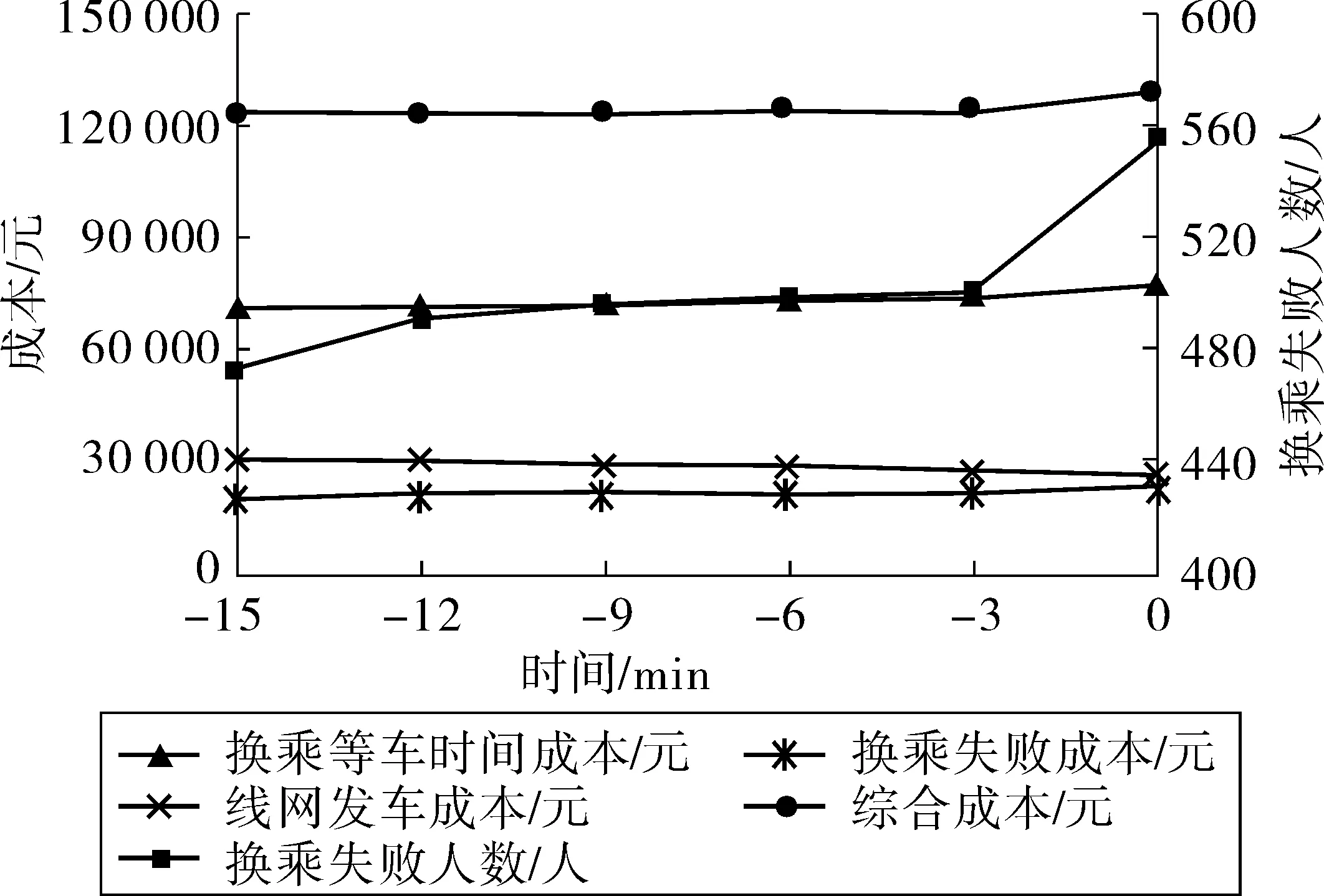
0 (9) 3.3.3 发车间隔时间约束 时段内列车的发车间隔时间应该按照规定控制在最大值与最小值的范围之内,且相邻两列车的发车时间间隔应该等于发车间隔时间,如式(10)、式(11): th,min≤Hi≤th,max (10) D1iq=D1i,q-1+Hi (11) 式中:ht,max,th,min为各线路发车间隔时间的上下限;Hi为线路i在首末班车时段的发车间隔时间,每条线路在时段内的发车间隔时间为定值。 3.3.4 列车停站、运行时间约束 列车停站时间的取值应该在列车规定停站时间的最大、最小值之间。区间运行时间的取值应该小于列车最小速度时的最大运行时间且大于列车最大运行速度的最小运行时间,如式(12)、式(13): tp,ximin≤Pxiq≤tp,ximax (12) tr,ximin≤Rxiq≤tr,ximax (13) 式中:tp,ximax,tp,ximin为线路i上车站x的停站时间上下限;tr,ximax,tr,ximin为线路i上车站x的区间运行时间上下限。 3.3.5 首班列车发车时间约束 为了不影响后续早高峰的运营,首班车的发车时间应该在一定范围内,有约束如式(14): 0≤D1i1≤TD (14) 式中:TD为首班车发车时间上限。 3.3.6 首班车时段内列车的运行时间约束 首班车发车时段内发车数量也应该遵循相应的条件,即列车到达每一站点的时间都应该处于该时段内: T2f-T1f-Hi≤AXi,i1+(Ni,u-1)·Hi≤T2f-T1f (15) 式中:T1f、T2f为首班车时段的起止时间;AXi,i1为线路i上的首班车到达终点站Xi的时间。 城市轨道交通首班车时段的时刻表优化问题是一个复杂的组合优化问题,模型的变量多且约束复杂,解的空间大。遗传算法具有快速搜索全局最优解(或准最优解)的能力,执行简单灵活,被广泛应用于优化问题的求解。因此,笔者采用遗传算法进行模型求解,具体步骤如下: 步骤1染色体设计。模型的4个决策变量为线路首班车的发车时间、发车间隔时间、区间运行时间以及关键站的停站时间。考虑到首班车时段时刻表优化模型的搜索空间大、模型变量多,笔者采用实数编码方式进行编码[2,16],染色体编码如图4。 图4 染色体编码Fig. 4 The encoding illustration of a chromosome 步骤2初始化种群。输入模型数据与算法参数,采用随机初始化的方式在各变量的约束范围内生成初始种群。 步骤3计算适应度函数值。计算种群中每一个染色体的适应度函数。采取以目标函数转化为适应度函数的转换方式,适应度函数Fit(F)设置为目标函数F的相反数,即: Fit(F)=-F (16) 步骤4选择运算。根据适应度大小,选取适应度为前5%的染色体进入到下一代种群,其他的染色体采用轮盘赌算子进行选择,产生新一代种群。 步骤5交叉运算。以交叉概率Pc对染色体进行两点交叉操作[2],在相互配对的两个染色体中随机设置两个交叉点,然后交换其所设定的两个交叉点之间的部分基因。 步骤6变异运算。对种群中的染色体以变异概率Pm随机选取进行变异操作[2],产生出新一代个体,得到下一代种群。 步骤7检验是否满足终止条件。采用最大迭代次数或个体适应度无法再进行有效的改进作为算法的终止条件。如果满足终止条件,则终止计算输出最优方案;否则,返回步骤3。 笔者将2014年深圳地铁线网作为研究对象,线网由5条线路、131座车站(含13座换乘站)组成。简化后的线网拓扑如图5,图5中箭头表示线路的上下行方向。 图5 深圳地铁线网拓扑Fig. 5 Network topology of Shenzhen metro 深圳地铁线网的乘客刷卡数据、发车间隔时间、区间运行时间、列车停站时间、最早发车时间等数据均从地铁公司获取。首班车时间段接近早高峰,根据客流特点和运营要求,首班车时段换乘站停站时间设定其上下限分别为1 min和0.5 min;发车时间间隔在高峰和平峰之间,取3~7 min之间。深圳地铁换乘站的乘客平均换乘走行时间通过调查得到,如表1。当乘客换乘等车时间大于Tij,C时,视为首班车时段的换乘失败行为,换乘失败惩罚值60 min。 表1 乘客换乘走行时间Table 1 Passenger transfer walking time 基于AFC刷卡数据,通过考虑乘客车内时间与换乘时间(包括换乘走行时间和换乘等车时间)的时间效用Logit模型将客流分配到有效路径之上,任意OD对的有效路径为最短路和次短路。最短路和次短路分配的客流量可以达到95%以上。将所有客流量分配到最短和次短路上较为符合实际的客流情况,误差在可接受范围之内[17]。 模型的成本参数主要有两个:时间费用转换系数δ和线路i上每发出一列班车的发车成本Gi。时间费用转换系数=深圳市人均月薪/月平均工作时长(数据来自2014年深圳社保网中的深圳社保局通知),经计算得出δ取值为44元/h,即0.73元/min。发车成本包含电力成本、设备损耗以及人力成本等,笔者主要考虑列车牵引的电力成本,根据文献[16],牵引一列车的电力成本为12元/km。 5.3.1 遗传算法的迭代过程 遗传算法在MATLAB中编程执行。算法的参数值设置如下:种群规模取值为200;交叉概率值设定为0.8;变异概率设定为0.05;最大迭代次数为500次。代入模型的参数,输入相应的数据,得出优化的决策变量值与首班车时段时刻表。图6表示模型的目标函数值在迭代过程中的变化。由图6可知,在100代之前目标函数值降低较快,在400代之前达到收敛。 图6 总成本的迭代过程Fig. 6 Iteration process of total cost 5.3.2 成本分析 首班车时段模型的优化结果如表2。首班车时段优化前乘客换乘等车成本为77 687元,线路发车成本为26 628元,总成本为128 612元。经过优化后,乘客换乘等车时间成本为64 004元(降低了17.6%),线网发车成本为15 552元(减少了41.6%),总成本为99 556元(降低了22.6%)。模型对成本的优化效果较为显著。 表2 优化前后的成本对比Table 2 Comparison of cost before and after optimization 5.3.3 乘客换乘失败分析 首班车不存在线网时空的可达性问题,但是首班车会出现换乘等待时间过长的情况,笔者将这一情况同样视为换乘失败。由于AFC刷卡数据只记录了乘客的进出站信息,但无法直接得到乘客换乘失败的状态。基于模型对换乘失败的定义,将客流数据与现状时刻表进行匹配运算,得出优化前后的乘客换乘失败情况,如表3。首班车时段的乘客换乘失败成本从优化前的24 297元降到了20 000元,换乘失败人数从555人减少到了457人,优化率达到了17.7%。可见该优化模型能有效改善首班车的换乘失败行为。 表3 优化前后乘客换乘失败比较Table 3 Comparison of passenger transfer failure before andafter optimization 由于区间运行时间与列车的设计车速与运行能耗关系密切,因此,笔者仅对发车间隔、停站时间和发车时间3个运营参数进行敏感性分析。 5.4.1 发车间隔 为了分析发车间隔对首班车时段列车间换乘协调的影响,将停站时间与区间运行时间固定,调整线路的发车间隔,优化结果如表4 。通过调整发车间隔,可以实现网络间的换乘协调,减少乘客的换乘等车时间成本、换乘失败成本和发车成本。发车间隔的调整对换乘等车时间成本和发车成本影响较大,而对换乘失败人数的影响较小。调整发车间隔可以降低换乘人数,但是减少的幅度比较接近。 表4 发车间隔敏感性分析Table 4 Sensitivity analysis of departure interval 5.4.2 停站时间 为了分析优化结果对停站时间的敏感性,将发车间隔和区间运行时间固定,对停站时间进行调整,优化结果如表5。换乘乘客的换乘等车成本和换乘失败人数对停站时间较为敏感。由于线网中存在多个换乘站,通过对列车的停站时间进行调整,可使多个换乘站的列车同时实现协调衔接。停站时间对发车成本的影响较小。 表5 停站时间敏感性分析Table 5 Sensitivity analysis of stopping time 5.4.3 发车时间 首班车最早发车时刻约束直接影响时刻表的优化效果,分析该参数对时刻表优化效果的影响,可以为运营公司选择各线路的发车时刻提供依据。首班车发车时间约束在原时刻表基础上分别提前3、6、9、12、15 min,分析不同取值下目标函数的优化效果(如图7)。取值的含义为,与现行时刻表的最早发车时刻 06:30 相比,优化时刻表最早发车时刻的变化量。 图7 发车时间敏感性分析Fig. 7 Sensitivity analysis of departure time 随着地铁网络首班车最早发车时刻的提前,目标函数优化效果更加明显,可减少换乘失败人数。首班车发车时间提前得越早,换乘衔接失败的人数越少,但首班车发车时间的提前会导致企业运营成本增加。因此,首班车发车时间需兼顾网络服务水平与企业运营成本,运营企业应根据实际情况决定线路首班车的发车时间。 笔者遵循城市轨道交通早间运营时段的客流特性,研究列车间的换乘衔接优化问题,在满足相关运营要求和时刻表模型约束的基础上,考虑首班车换乘失败行为,以乘客换乘等车成本和线路发车成本最小为目标,构建首班车时段的时刻表优化模型。笔者设计的遗传算法可以有效求解首班车时刻表优化问题。笔者通过深圳地铁网络进行实证分析,验证了模型的可行性。结果表明,该模型能有效地生成城市轨道交通首班车时段列车协调衔接时刻表,为相关部门提供决策支持。但是,笔者简化了乘客的路径选择问题,基于最短路和次短路搜索有效路径。随着轨道交通网络规模的扩大,可供选择的换乘路径增加,乘客对路径选择也存在差异性。在线网运营成本中只考虑了线路的发车成本,而运营成本由多项成本构成。这些问题还有待深入研究。4 求解算法设计
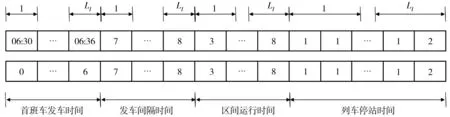
5 案例分析
5.1 深圳地铁线网概况

5.2 基础数据及模型参数

5.3 首班车衔接优化结果分析

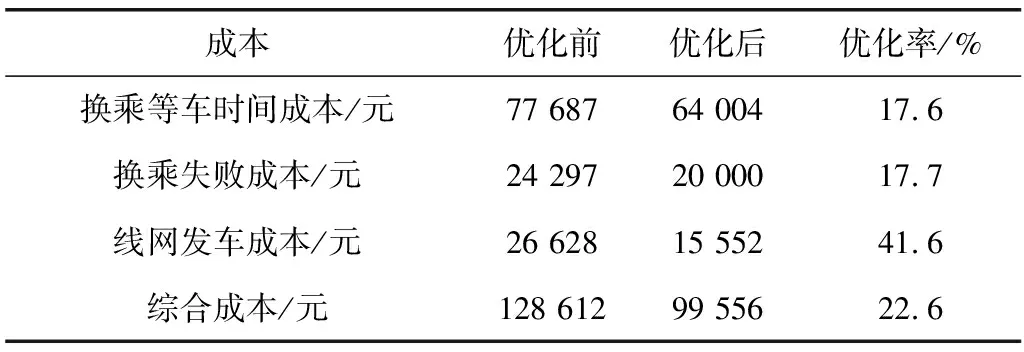
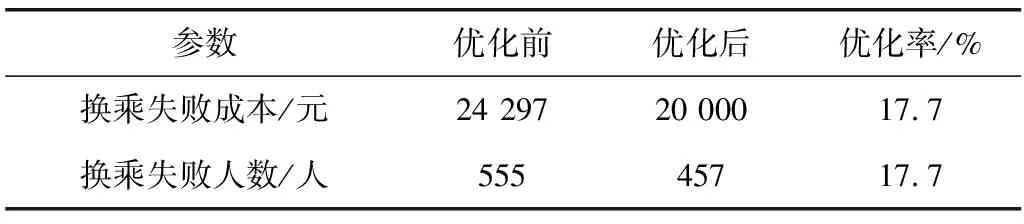
5.4 敏感性分析

6 结 语

