基于大数据方法的持液率预测模型
郑 琳 刘 云
长江大学石油工程学院, 湖北 武汉 430100
0 前言
管道中气体和液体的两相流在石油工业中经常发生,多相管流一直是石油工业中的一个重要问题[1]。持液率是指管道内实际的液体体积分数,是计算压力损失时最重要的参数,同时也对预测水合物的形成和蜡的沉积十分重要[2]。对于持液率的预测,国内外学者提出了大量的机理模型和经验模型,部分使用较普遍,而另一部分的应用范围则较窄。大部分的方法都始于流态的预测,每种流态都有相关的预测持液率方法,但这种方法取决于流型预测的准确性,且在跨流型过渡边界,会出现预测模型不连续问题,模型随着流动条件的变化会出现差异,使得选择最合适的流动相关性模型具有挑战性。
持液率与其影响参数之间是一种非线性关系,与神经网络模型所表达的解决非线性映射问题的思想相吻合[3]。Osman E A[4]开发的神经网络模型使用4个输入参数,即气体表观速度、液体表观速度、压力和温度,包含12个隐含层节点。Shippen M E等人[5]排除气体密度、气体黏度、管壁粗糙度等几个对持液率影响可忽略的变量,并加入无滑移持液率共7个输入层变量,包含8个隐含层节点,都与现有的经验模型和机理模型预测的持液率结果进行了比较,证实神经网络模型在预测持液率方面是最准确的。但是Osman E A使用的输入参数中没有包括流体特性,这就代表只能应用于具有类似实验特性的流体中。Shippen M E在此基础上进行了改进,加入流体特性,使模型的使用范围不再局限于特定流体特性,但还是受到了训练数据范围的影响。在这些情况下,我们采用大数据统计的方法并使用Eaton B A提出的流体特性相关无因次数作为输入参数,扩大模型的使用范围。建立好的GA-GRE-BP神经网络模型经过大数据集训练后得到持液率预测公式,最后利用随机得到的70组实验数据验证了新模型的准确性。
1 GA-GRE-BP神经网络模型
1.1 BP神经网络的构建
Ros N C J[6]在大量实验和理论工作的基础上,排除了持液率可以忽视的,气体密度,气体黏度和壁面粗糙度等几个变量。Shippen M E等人[5]也在神经网络模型的研究过程中证实这些变量的影响较弱,可忽视。其余不可忽视变量包括液体表面张力、管径、液体黏度、气体表观速度、液体表观速度和液体密度。考虑到数据的局限性,为了扩大BP神经网络模型的使用范围,决定利用Eaton B A等人[7]提出的无因次参数量作为BP神经网络的输入变量,对数据有较好的适应性。
Eaton B A等人提出的持液率相关公式为:
(1)
式中:Ψ为任意函数;HL为持液率;Nlv为液体速度影响数;Ngv为气体速度影响数;Nd为管径影响数;p为绝对压力,MPa;pb为测量气体的基准压力,MPa;Nl为液体黏度影响数;Nlb为基础黏度影响数,取0.002 26。
除了选取气体速度影响数、液体速度影响数、管径影响数和液体黏度影响数以外,还加入了压力影响因素,共5个因素作为输入层变量。
BP神经网络模型建立的关键环节是隐含层的个数,为了避免过多或过少的隐含层神经元个数对神经网络模型的建立带来的不利影响,隐含层神经元的个数通过以下的经验公式确定[8]:
(2)
式中:m为隐含层神经元的个数;n1为输入层神经元的个数;n2为输出层神经元的个数;a为0~10之间的常数。
经过反复测试对比,确定隐含层神经元的个数为7,当隐含层激活函数为S型且输出范围在-1~1的‘tansig’函数,输出层激活函数为线性输出的‘purelin’函数,选择训练函数来导出动量并自动调整学习率旋转梯度递减函数为‘trainlm’的时候准确度最高,最终确定神经网络模型为5×7×1的三层感知器的结构形式,图1为持液率的神经网络示意图。

图1 持液率的神经网络示意图Fig.1 Neural network diagram of liquid holdup
1.2 GRE-BP神经网络的构建
灰色关联熵分析是熵权法与灰色关联度相结合的一种模型。熵权法的引入不仅降低了灰色关联度系数的波动性影响,也提高了灰色关联分析法的计算精度[9]。经过灰色关联熵处理过的参数用于BP神经网络模型的训练降低模型预测误差,从而弥补基本的BP神经网络存在的缺点。
1.2.1 熵权法
熵权法是一种利用信息熵来度量影响持液率各个因素的客观赋权法,一个因素的信息熵越小,其无序化程度就越大,表明它所提供的有用信息越多,对持液率的影响力越大,权重也就越高。熵权是由各影响因素信息效用值确定的[9]。熵权的运算步骤如下:
1.2.1.1 标准化处理
(3)
式中:yij为经过标准化处理的第i个单位第j个因素值;xij为第i个单位第j个因素数据原始值;xjmin为第j个因素的最小值;xjmax为第j个因素的最大值。
1.2.1.2 定义标准化
(4)
式中:Yij为经过定义标准化处理的第i个单位的第j个因素的值。
1.2.1.3 因素的信息熵值计算
(5)
式中:ej为第j个因素的信息熵值。
1.2.1.4 影响因素的信息效用值计算
dj=1-ej
(6)
式中:dj为第j个因素的信息效用值。
1.2.1.5 评价影响持液率因素的权重
(7)
式中:wj为第j个因素的权重。
1.2.2 灰色关联度分析
灰色关联度能反映两种指标之间的相关程度。简单来讲,把持液率作为参考序列,而影响持液率的5项指标就是比较序列,最后通过灰色关联度分析可以得到这5项指标分别与持液率的相关程度,灰色关联度越大,说明它对持液率结果的影响力越大。灰色关联度的运算步骤如下:
设Xi={xi(k)|k=1,2,…,n}为比较序列,X0={x0(k)|k=1,2,…,n}为参考序列。
1.2.2.1 数据无量纲化处理
消除不同因素序列可能存在量纲不同而产生的差异,需要对原始数据进行无量纲化处理。
1.2.2.2 求差序列
Δ=|x0(k)-xi(k)|,k=1,2,…n
(8)
式中:Δ为各时刻xi与x0的绝对差值。
1.2.2.3 计算灰色关联系数
(9)
式中:ξi(k)为第i个比较序列第k个指标与参考序列第k个最优指标值的关联系数;ρ∈(0,1)为分辨系数,一般取0.5;Δmin为两级最小差,且Δmin=miniminkΔ;Δmax为两级最大差,且Δmax=maximaxkΔ。
1.2.2.4 计算灰色关联度
(10)
式中:γi为第i个比较序列的灰色关联度。
通过熵权法与灰色关联度的结合,求得灰色关联熵公式如下:
hi=wj×γi
(11)
式中:hi为第i个指标的灰色关联熵。
1.3 GA-GRE-BP神经网络的构建
由于学习效率低和容易陷入局部最小值等问题仍然存在于GRE-BP神经网络中,为了避免这些情况的发生,利用遗传算法可以全局寻优的特点对神经网络的权值和阈值进行优化,同时也能加快算法收敛的速度,缩短网络训练的时间[10]。
遗传算法是借鉴生物界进化规律设计的算法,它通过数学方式,利用计算机编码完成染色体的选择、交叉和变异,从而求取最优个体。遗传算法个体的编码长度取决于优化的权值和阈值的个数,并最终由最佳GRE-BP神经网络中输入和输出的参数个数决定[3]。最后被遗传算法优化后的权值和阈值用于GRE-BP神经网络训练。
GA-GRE-BP神经网络模型流程见图2。
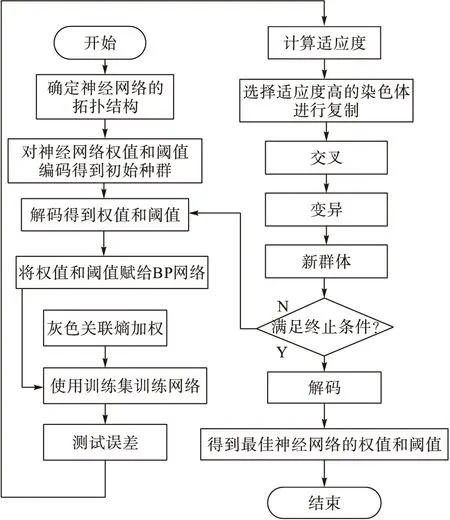
图2 GA-GRE-BP神经网络模型流程图Fig.2 Flowchart of GA-GRE-BP neural network model process
2 模型验证
完成GA-GRE-BP神经网络模型的建立后,将众人研究的4 010组数据用于开发气液两相流动中持液率的神经网络预测模型,随机选出70组数据作为测试集,用于测试该神经网络模型的准确性,剩余3 940组数据作为训练集,用于训练该神经网络模型。表1为实验数据的来源以及一些流动参数的有效范围。
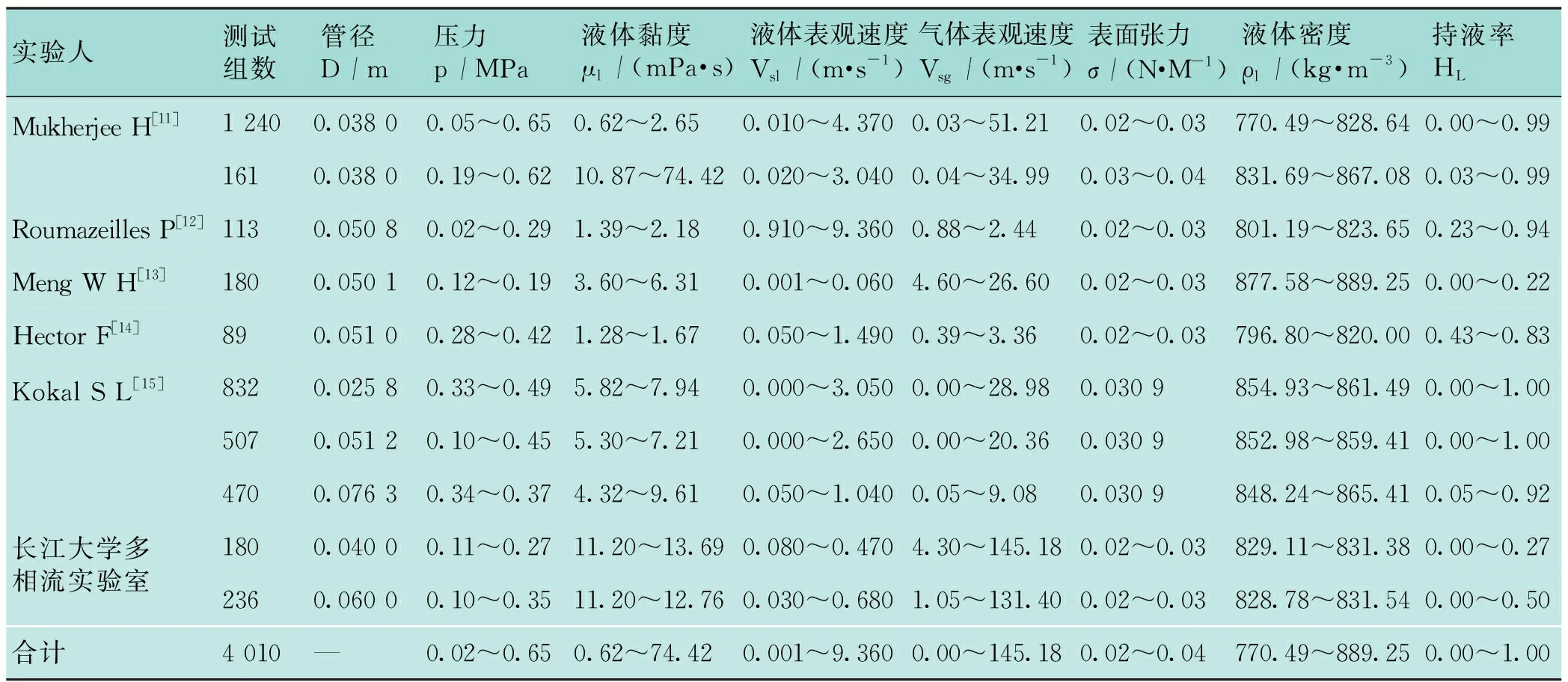
表1 实验数据汇总表
以上实验室数据通过长江大学多相流实验平台得到,此平台可开展在不同倾角、不同温度和压力等多个条件下,对油、气和水三相混合介质多相管流动态研究,实验流体为白油和空气,通过实验系统的动力系统、管路系统、控制系统、储存系统和数据采集系统等共同完成[16]。
2.1 交叉验证
神经网络几乎依靠数据单纯的训练并记忆,不能够对数字本质进行理解并泛化到测试集上,本质只是一个经验性的模型。因此选取交叉验证的方式来评估优化后的模型。K折交叉验证误差取决于K值的大小,K值较小时,误差较大,当K值较大时,与留一法交叉验证相当,鉴于留一法交叉验证的过程较长,采用与留一法交叉验证更接近的10折交叉验证[17]。
10折交叉验证是把训练集里的3 940组数据均分成10个不相交的子集,每一个子集里有394组训练数据,依次从分好的子集里面,拿出1个作为验证集,其他9个作为训练集训练神经网络模型,并使用此验证集对训练算法的行为进行独立检查,最后平均10次的结果作为误差的估计,来判断模型的准确度。
2.2 验证结果
通过对GA-GRE-BP神经网络模型进行训练、验证,得到与模型相关联的权值和阈值,见表2~3。

表2 输入层、隐含层和输出层之间的权值表

表3 隐含层和输出层的阈值表
将得出的权值和阈值与持液率预测模型的嵌套数学公式结合,得到持液率的预测公式如下:
(12)
式中:HL为持液率;Wij为第i个输入层元素到第j个隐含层元素之间的权值;Bj为第j个隐含层元素的阈值;xi为输入层的第i个元素;Wjk为第j个隐含层元素到第k个输出层元素之间的权值;Bk为第k个输出层元素的阈值。
(13)
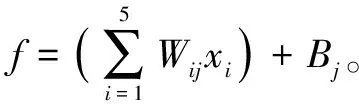
3 模型预测
为了对GA-GRE-BP神经网络模型的准确性以及可行性进行评估,将其与基本的BP神经网络模型,以及Beggs-Brill[18]和Minami-Brill[19]提出的传统模型进行对比。表4是各指标的灰色关联熵,用于GA-GRE-BP神经网络模型的预测。
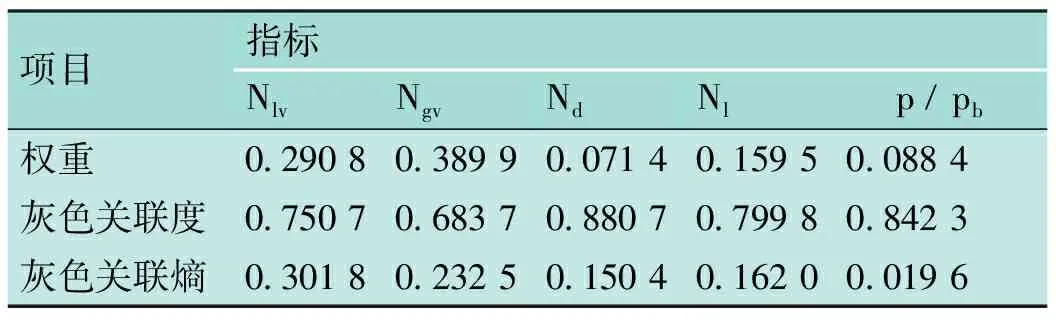
表4 各指标的灰色关联熵表
图3为持液率的实际值与各模型预测值对比结果。从图3可以看出,Minami-Brill的模型在持液率较低和较高的范围内预测结果较好;Beggs-Brill的模型虽然在整个持液率的范围内预测结果较好,但仍然存在许多误差较大的预测点;BP神经网络模型和GA-GRE-BP神经网络模型的预测值均在实际值曲线附近,整体来看,GA-GRE-BP神经网络模型预测结果更好。
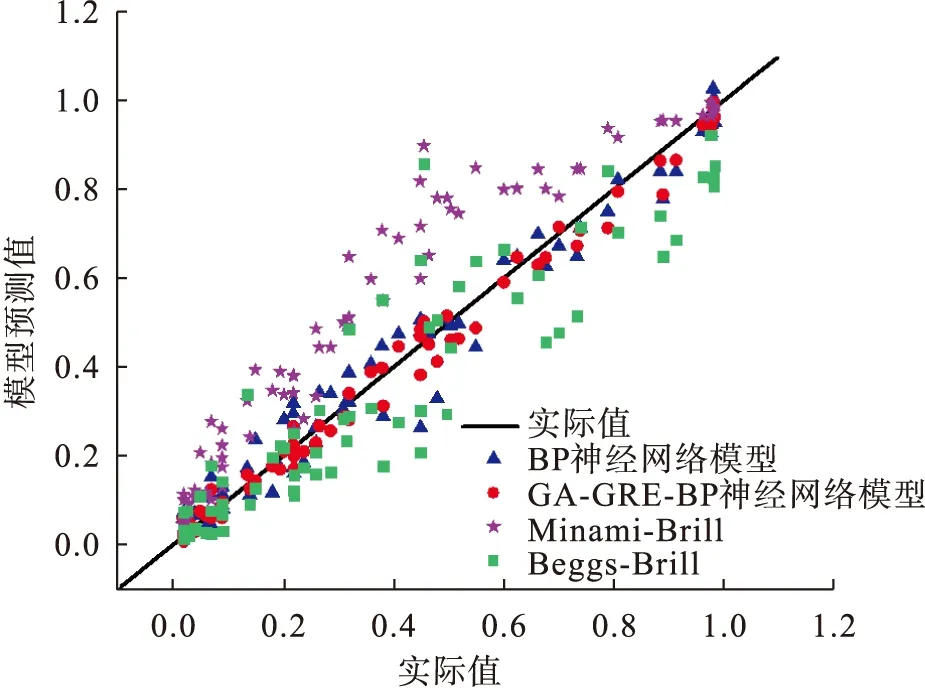
图3 四种模型预测对比结果图Fig.3 Four models predictions and comparison results
为了更好地进行模型对比,同时采用Mandhane J M[20]等人提出的五种不同误差测量方法来评估预测的准确性。
1)均方根误差:
(14)
2)平均百分比误差:
(15)
3)平均绝对百分比误差:
(16)
4)绝对值平均绝对误差:
(17)
5)平均绝对误差:
(18)
式中:ei为持液率预测值与实际值的差值,即ei=(HLpred-HLmeas)i,i=1,2,…,n;HLpred为持液率预测值;HLmeas为持液率实际值。
四种持液率预测模型的误差对比见表5,由表5可看出,BP神经网络模型比传统模型的预测更精确,而GA-GRE-BP神经网络模型相较于BP神经网络模型,误差均降低了40%以上,提高了模型的精确度。
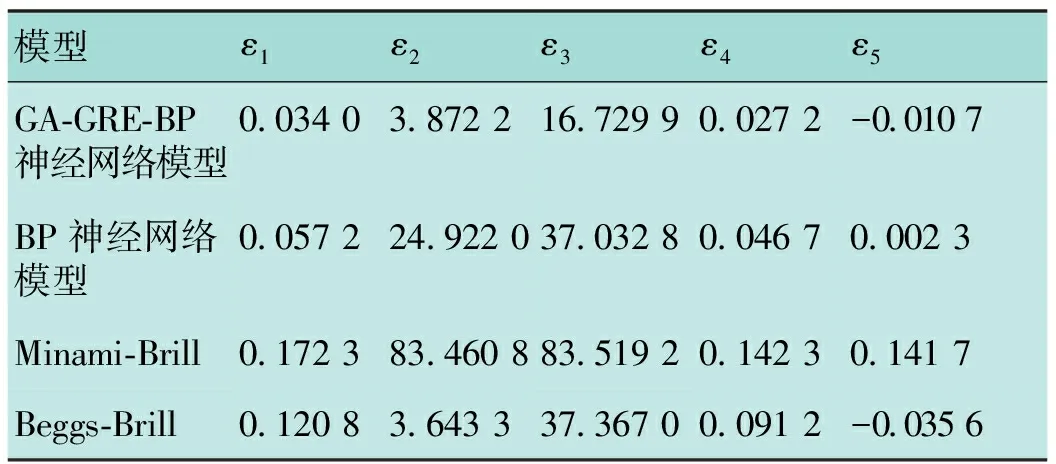
表5 四种持液率预测模型的误差对比表
综上所述,GA-GRE-BP神经网络模型不仅精确度高,而且应用范围广,可以用来预测持液率。
4 结论
1)GA-GRE-BP神经网络模型预测气液两相流持液率,利用庞大的数据体系,数据来源多样化,更有效地预测处于各种流体特性下气液两相流的持液率。将Eaton B A等人提出的无因次参数作为输入层变量,不仅解决了数据局限性问题,也使得模型的适应性更好。
2)经过大数据集训练的GA-GRE-BP神经网络模型,最终得到了一个嵌套型数学公式,可以直接用于气液两相流持液率的预测。
3)基于大数据方法的GA-GRE-BP神经网络模型弥补了基本BP神经网络模型预测误差大,容易陷入局部极值的缺点,它的精确度更高,收敛速度更快;弥补了传统模型应用范围的狭窄,迭代计算复杂的缺点,它的应用范围更广泛,使用更简便。
4)基于大数据方法的GA-GRE-BP神经网络模型是依靠大量数据,单纯训练学习的一个过程,如何对已有数据进行处理并加以充分利用,提高精确度,是后续要完善的一项任务。

