挤压油膜阻尼器在锥齿轮系统中减振特性分析
邢 彬,王秋菊,牟佳信,陈维涛,陈思雨
(1.中国航发沈阳发动机研究所航空发动机动力传输重点实验室,沈阳110015;2.中南大学高性能复杂制造国家重点实验室,长沙410083)
0 引言
现代航空发动机高压转子转速高达40000 r/min,使得与高压转子相联的中央传动齿轮系统的工作转速通常高于转子系统的第1阶临界转速。中央传动锥齿轮在进入工作转速之前会通过转子系统的第1阶临界转速,而转子在临界转速附近的振幅较大,由此带来的振动问题成为影响发动机安全的重要因素[1],甚至会造成机器损伤或破坏事故[2-3]。为改善发动机齿轮系统的振动特性,主要有2种思路:一是主动减振,如优化齿轮设计参数以提高其传动及接触性能[4],提高制造精度、进行齿廓修形[5-7]以减小传动误差,从而达到减振效果,但该方法会增加制造成本,且难以确定合适的修形参数;二是被动减振,通过在齿轮系统中增加阻尼环[8-10],或采用弹性支承代替刚性支承,典型的是采用鼠笼式弹性支承和挤压油膜阻尼器(Squeeze Film Damper,SFD)组合使用[11-12],其中,SFD通过添加阻尼来耗散振动能量,鼠笼降低滚动轴承的支承刚度,因此具有调频功能,避免转子发生弯曲临界振动。
航空发动机转子系统在SFD支承下的动力学特性研究吸引了众多学者的关注。陈会征[13]研究了转子-滚动轴承-SFD系统非线性动力学,建立刚性转子-SFD的动力学模型和油膜力模型,得到系统分岔方程,并进行奇异性分析;张薇等[14-15]以转子通过临界转速时的振幅、外传力及减振效果为目标,以弹性支承刚度及油膜间隙为设计变量,采用胞映射算法进行了多目标优化设计,并通过试验验证了这种方法在转子-SFD系统设计中的可行性;祝长生等[16-17]、WANG等[18]、廖明夫等[19]通过试验研究了SFD在航空发动机转子系统中的减振特性及减振机理。上述研究发动机转子-SFD系统时没有考虑齿轮的作用,而实际上齿轮系统除了增加转子系统的不平衡偏心量及陀螺效应激励外,齿轮副之间传动误差、时变啮合刚度等因素亦对其有影响。因此,相比转子-SFD系统,齿轮-SFD系统更为复杂。杨海燕等[20]采用传递矩阵法研究了定心型SFD及弹性支承在航空发动机锥齿轮-转子系统中的减振作用;何立东等[21-23]构建了锥齿轮及整体式SFD试验台,通过试验表明SFD在锥齿轮系统中的振动降幅可达40%,但未在理论方面深入研究;李明等[24]、CHANG[25]采用短轴承近似解析解计算SFD的非线性油膜力,并研究了齿轮系统在SFD支承下的动力学特性,由于采用集中质量法进行动力学建模,未考虑柔性齿轮轴影响。
为改善上述研究中的不足,本文采用有限元方法计算SFD的非线性油膜力,并对SFD支承下的弧齿锥齿轮系统进行动力学建模,搭建弧齿锥齿轮-SFD试验台,对SFD在弧齿锥齿轮系统中的减振特性进行理论和试验研究。
2 弧齿锥齿轮-SFD系统动力学模型
本文研究的航空发动机中央传动锥齿轮系统结构(如图1所示)主要由壳体、大齿轮、小齿轮、轴承座及轴承组成。锥齿轮副中大齿轮为主动轮、齿数55齿,小齿轮为从动轮、齿数47齿,齿轮设计参数见表1。大、小齿轮轴两端均采用滚动轴承支承。为改善中央传动锥齿轮系统的振动性能,将大齿轮轴靠近齿轮一端的支承由滚动轴承改为鼠笼式弹性支承及SFD支承,改进后的结构如图2所示。鼠笼式弹性支承和4点接触球轴承是串联关系,由于4点接触球轴承的刚度量级为108~109N/m,鼠笼式弹性支承的量级为107N/m,串联后的等效刚度接近鼠笼式弹性支承的刚度,4点接触球轴承的刚度与鼠笼式弹性支承相比可以近似为刚性,可将齿轮轴、4点接触球轴承与弹性支承看作一体。

图1 刚性支承下的中央传动锥齿轮系统结构
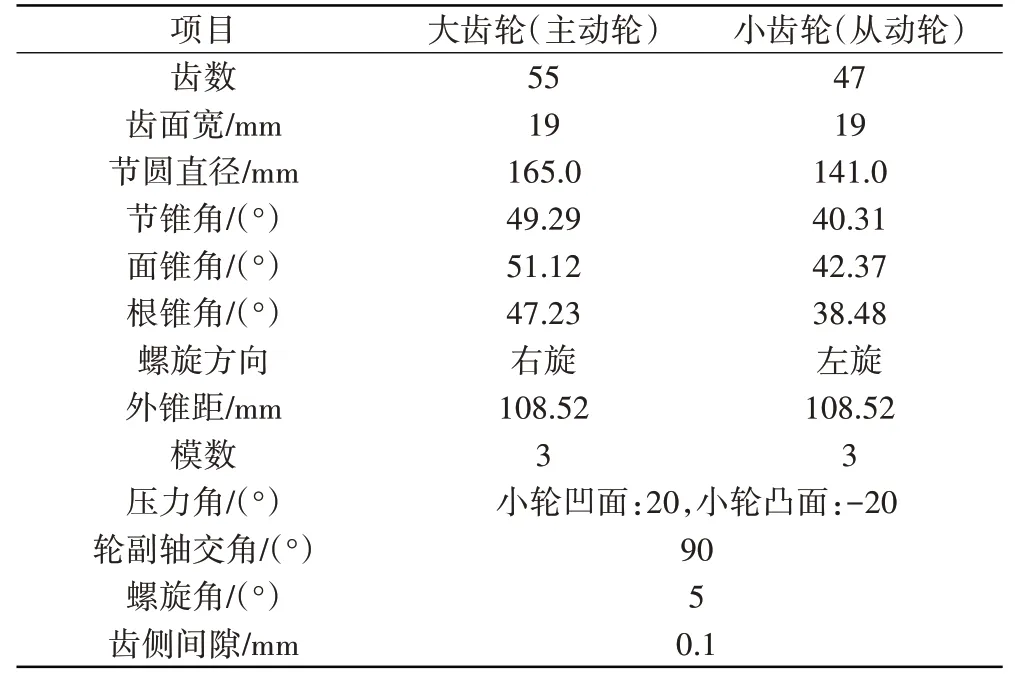
表1 齿轮设计参数

图2 弹性支承下的中央传动锥齿轮系统结构
2.1 弧齿锥齿轮系统动力学建模
2.1.1 轴系建模
采用有限单元法及Timoshenko梁单元对齿轮系统进行动力学建模。Timoshenko梁单元假设变形时梁的横截面保持为平面并且截面不变形。但弧齿锥齿轮属于对称结构、非对称受力和变形,齿轮啮合时会出现局部轮齿及腹板变形。为简化计算,本文采用Timoshenko梁单元对齿轮轴建模时假设轮齿不变形和腹板变形后截面仍为平面,但这些假设不可避免地带来误差。对于主动齿轮轴(其建模如图3所示),根据轴的外径大小分为2段L1和L2,每段又分成若干个梁单元。为表示大锥齿轮的节锥锥度,将锥齿轮沿轴向方向划为5段(L3~L7),每段采用Timoshenko梁单元进行建模,这样锥齿轮的锥度、刚度、质量、陀螺力矩及阻尼效应均包含在动力学模型中。
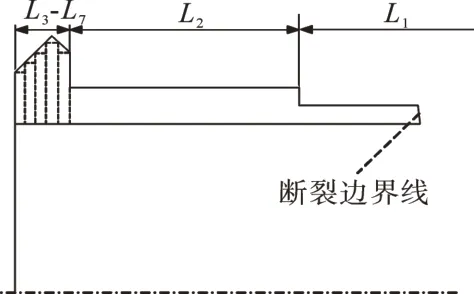
图3 主动齿轮轴建模
对于从动齿轮轴,由于小齿轮采用的是薄腹板,并且有一定的弧度,如果与主动锥齿轮采用同样的多段梁单元来表示锥齿轮的锥度会产生不小的计算偏差,因此采用柔性齿轮轴及刚性齿轮盘结合的方法来对从动齿轮轴进行建模,如图4所示。首先根据从动轴的外径尺寸将轴分成3段,每段用多个梁单元进行建模;其次将刚性齿轮盘的质量、陀螺属性根据节点编号装配到齿轮轴中。
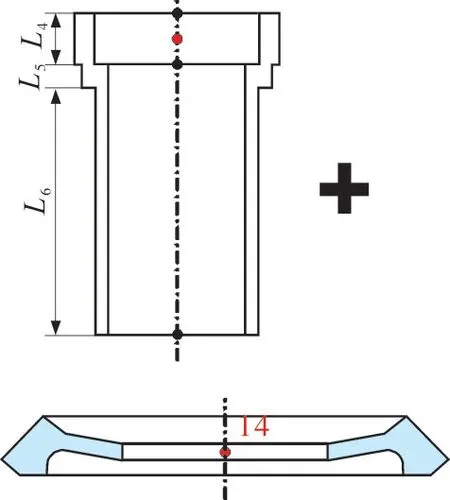
图4 从动齿轮轴建模
任意Timoshenko梁单元由2个节点和12自由度组成,其质量矩阵M12×12、刚度矩阵K12×12、阻尼矩阵C12×12和陀螺矩阵G12×12是梁单元长度、外径、内径和转速的函数,可由拉格朗日方程推导[6,26,27]。
对主动齿轮轴和从动齿轮轴各单元节点进行编号,如图2所示。根据单元节点编号顺序将所有Ti⁃moshenko梁单元组装成轴系总体质量矩阵Ms、总体刚度矩阵Ks、总体阻尼矩阵Cs和总体陀螺矩阵Gs[28]。中央传动锥齿轮系统由1个弹性支承、2个4点接触球轴承支承及2个圆柱滚子轴承支承(图2),总体支承刚度矩阵Kb可以根据轴承和弹性支承的节点编号顺序组装得到,即其中Kb1、Kb3、Kb4分别为图2中轴承1、3和4的支承刚度矩阵。并且1,3,4,轴承刚度矩阵中元素kbxl、kbyl、kbzl、kbqxl、kbqxl、0分别为滚动轴承在水平x方向、竖直y方向、轴向z方向、绕x轴摆动方向、绕y轴摆动方向及绕z轴转动方向上的支承刚度。弹性支承刚度Ke=矩阵中元素kex、key、kez、keqx、keqy、0分别为弹性支承在水平x方向、竖直y方向、轴向z方向、绕x轴摆动方向、绕y轴摆动方向及绕z轴转动方向上的支承刚度。将总体刚度矩阵Ks和总体支承刚度矩阵Kb进行叠加获得系统的整体刚度矩阵
2.1.2 齿轮副耦合作用
主动齿轮轴和从动齿轮轴通过齿轮副进行耦合,如图5所示。齿轮副之间通过轮齿啮合点法向上的时变啮合刚度km和时不变啮合阻尼cm连接,并与静态传动误差es串联。为简化计算,忽略齿轮副啮合点位置和啮合点法向量随时间的变化,采用等效啮合点的位置向量和法向量,如图6所示。将小齿轮节锥与大齿轮节锥相交线的中点看作锥齿轮副的有效啮合点,其在小齿轮和大齿轮局部坐标系中的位置向量分别为xpm=[-rpm,0,0]和xgm=[rgm,0,0],此外,根据图6可以分别计算出有效啮合点相对小齿轮和大齿轮的法向量npm=[npx,npy,npz]和ngm=[ngx,ngy,ngz]。然后计算小齿轮和大齿轮的等效半径向量λl=[λlx,λly,λlz],其中l=p,g,并且λlx=-nlyzlm+nlzylm及λlz=-nlxylm+nlyxlm。
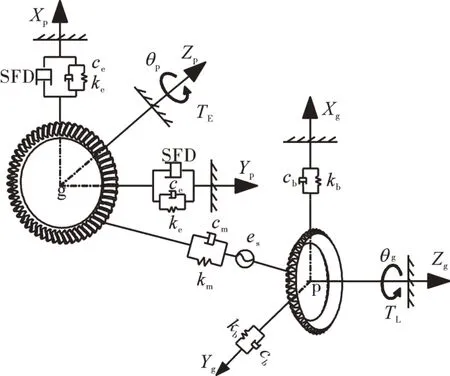
图5 弧齿锥齿轮副啮合
构建向量h=[npx,npy,npz,λpx,λpy,λpz,ngx,ngy,ngz,λgx,λgy,λgz]以及齿轮副的广义坐标向量x=[xpx,ypy,zpz,θpx,θpy,θpz,xgx,ygy,zgz,θgx,θgy,θgz],则锥齿轮副之间的动态传动误差ed=hx,齿轮副沿啮合线方向上的相对位移δr=ed-es,锥齿轮副之间沿啮合线方向上的动态啮合力为
式中:km为时变啮合刚度;cm为时不变啮合阻尼为齿侧间隙函数
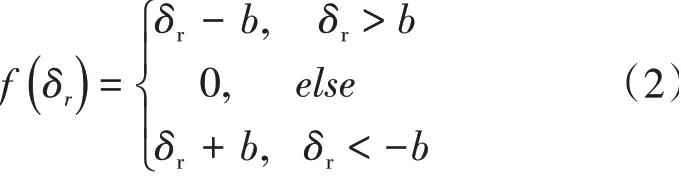
式中:b为齿侧间隙的一半。
主动轮和从动轮的质心与柔性齿轮轴相应的节点刚性连接,输入齿轮轴和输出齿轮轴之间只有动态啮合力的作用。因此动态啮合力对主动轮和从动轮在各自自由度上的分量可以表示为

齿轮系统的外部激励载荷

式中:TE为主动轴上激励扭矩;TL为负载扭矩。
弧齿锥齿轮-SFD系统除受到外部激励和动态啮合力外,还受到SFD的作用,SFD对弧齿锥齿轮系统的影响用SFD油膜反力在x和y方向上的分量Fx和Fy表示。采用Timoshenko梁单元对齿轮系统进行离散出现n个节点,每个节点有6个自由度,根据SFD节点编号顺序构建油膜力向量Fo
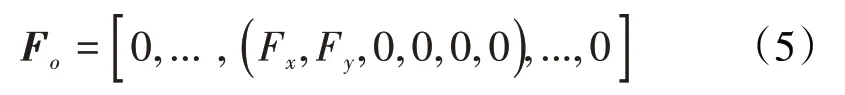
Fo共有6n个元素,SFD位于第i个节点,则Fx为Fo第(6i-5)个元素,Fy为Fo第(6i-4)个元素。将外部激励载荷向量Fe、SFD油膜反力向量Fo和动态啮合力向量Fm叠加得到系统整体激励向量F=Fe+Fo+Fm。
根据拉格朗日方程可得到航空发动机中央传动锥齿轮-SFD系统的运动控制方程[29],

式中:x为所有节点的广义坐标;Ω为齿轮轴的旋转角速度。
2.2 SFD非线性油膜力
弧齿锥齿轮系统中采用的SFD结构(如图7所示)主要由齿轮轴、滚动轴承、鼠笼式弹性支承、轴承座和油膜组成。弹性支承类似于悬臂梁,右端固定,左端作为SFD的轴颈。由于右端固定,左端只能在平面内平动,通过挤压油膜产生油膜阻尼。为便于计算,将轴承座简化为刚体并固定,滚动轴承内圈与齿轮轴、弹性支座的左端和外圈均为刚性连接。
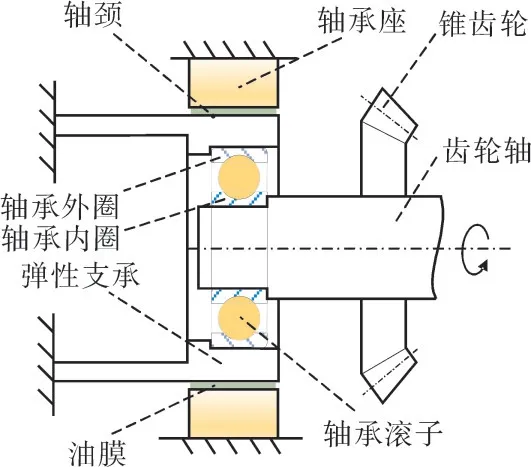
图7 挤压油膜阻尼器
SFD油膜压力控制方程为
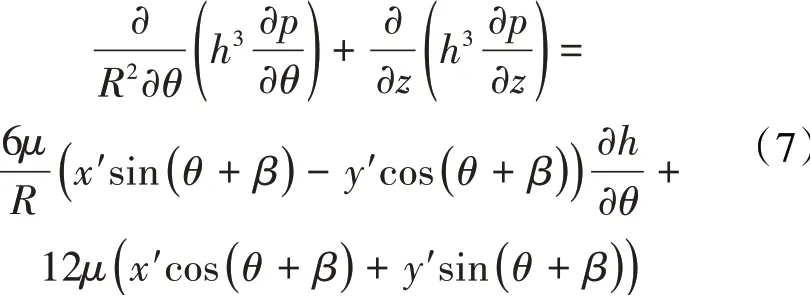
式中:R为轴颈半径;θ为周向位置坐标;p为油膜压力,为油膜压力;c和ε分别为SFD径向油膜间隙和轴颈偏心率;μ为流体动力黏度;β为偏位角;z为轴向位置坐标;轴颈在x和y方向上的振动位移分别为x和y,振动速度分别为x'和y'。
由SFD的Reynolds方程式(7)可知油膜反力为轴颈振动位移(x(t),y(t))和速度(x'(t),y'(t))的函数,即Fx,Fy=f(x(t),y(t),x'(t),y'(t))。将圆柱坐标系中SFD的油膜展开为笛卡尔坐标系下的油膜,并对其进行三角网格划分,如图8所示。采用有限元方法[30]计算SFD的油膜反力Fx和Fy。
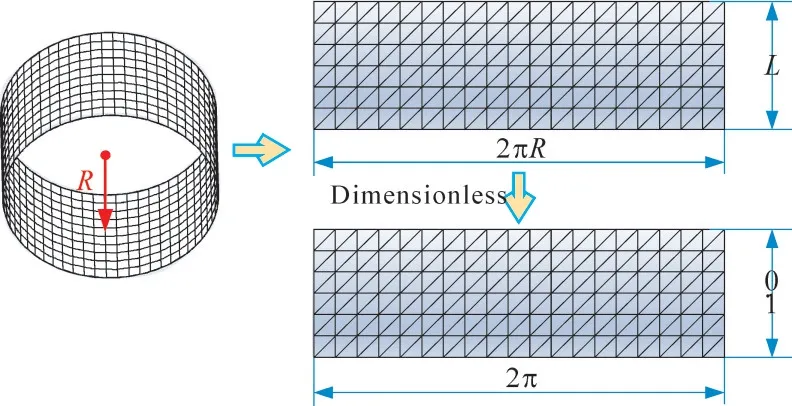
图8 SFD油膜三角形网格划分
2.3 齿轮副啮合刚度及静态传动误差
由齿轮动态啮合力公式可知弧齿锥齿轮系统中的主要振动激励源为静态传动误差和时变啮合刚度。借助有限元分析软件ABAQUS,有限元模型如图9所示。通过加载接触分析得到锥齿轮副的啮合刚度km
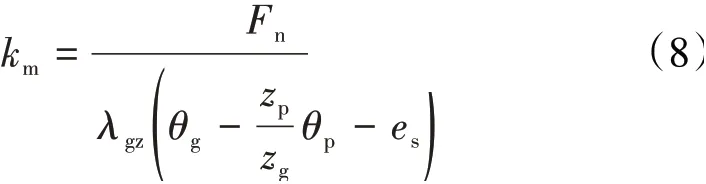
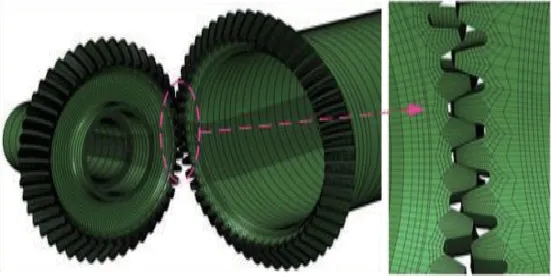
图9 弧齿锥齿轮副有限元模型
式中:Fn为齿轮副中同时啮合的多对齿轮法向啮合力;λgz为齿轮相对其坐标系的等效旋转半径;zp和zg分别为主动轮和从动轮的齿数;θp和θg分别为主动轮和从动轮相对各自局部坐标系的转动位移。
计算出的啮合刚度如图10所示。
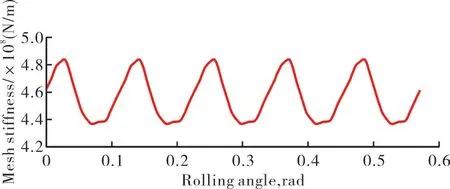
图10 弧齿锥齿轮时变啮合刚度
传动误差是齿轮系统振动和噪声的主要激励源之一,传动误差曲线的幅值大小和变化趋势直接反映到齿轮振动上,随着幅值的增大,振动、噪声也会逐渐增大,传动误差曲线变化越急促,振动也越大。对于齿轮副来说,传动误差为从动轮的实际转动角度与理论转动角度之差,而从动轮理论转动角度为主动轮实际转动角度乘以齿轮副传动比。齿轮传动误差可以被分为静态传动误差es和动态传动误差ed。静态传动误差主要反映齿轮副的加工制造精度,如切向综合误差、齿距累计误差、基节偏差、齿形误差等。通过3坐标测量机测量锥齿轮副的实际齿面(如图11所示),根据实际离散齿面点重构齿面,采用离散齿面无负载齿面接触算法[31]计算实际齿轮的静态传动误差。

图11 锥齿轮实际齿面测量
计算出的静态传动误差如图12中所示。频率成分主要由大齿轮第1阶轴频fs1和小齿轮第1阶轴频fs2组成,在中高频区间还有第1阶啮合频率成分fm,并且有很多“毛刺”信号,由无数小幅的边频成分构成。
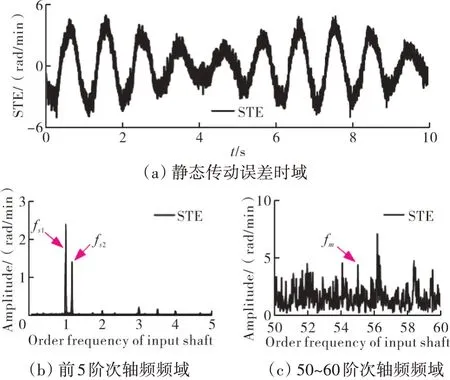
图12 锥齿轮副的静态传动误差
3 SFD减振特性分析
振动加速度是反映齿轮传动系统振动性能的重要指标。在8000、13400以及1000~16000 r/min升速3种工况下,分别分析在刚性支承和SFD支承时弧齿锥齿轮系统在支承处的振动加速度,通过对比验证SFD在弧齿锥齿轮系统中的减振效果。由于鼠笼式弹性支承及挤压油膜阻尼器安装在支承2处,因此SFD在弧齿锥齿轮系统中减振效果在支承2处表现得更为明显。锥齿轮系统在转速为8000 r/min工况时壳体表面支承2附近的振动加速度如图13所示。从图中可见,与刚性支承系统相比,通过增加SFD使得弧齿锥齿轮系统的振动加速度幅值大幅减小,振动加速度幅值减小19%。从图13(b)、(c)中可见,弧齿锥齿轮系统在支承2处的振动主要由3.5倍轴频、齿轮副的第1阶啮合频率fm(55倍轴频fs)、第2阶啮合频率fm(110倍轴频fs)、第3阶啮合频率fm(165倍轴频fs)、第4阶啮合频率fm(220倍轴频fs)及其轴频调制形成的边频带组成(51fs~58fs)。SFD主要抑制的是低频区域3.5倍频附近以及高频区域第2、4阶啮合频率附近的振动幅值,对其他频率成分振动的抑制并不明显。
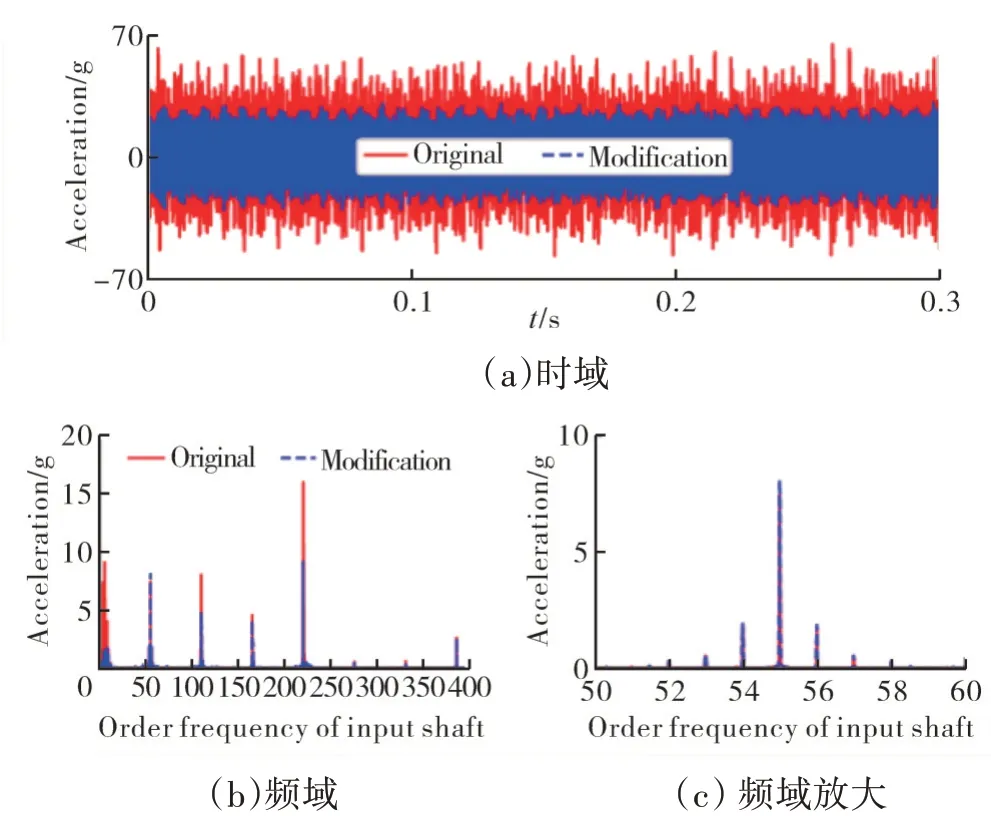
图13 转速为8000 r/min时支承2处的振动加速度
在高速工况转速为13400 r/min时弧齿锥齿轮系统在支承2处的振动加速度如图14所示。从图中可见,振动响应主要以前4阶啮合频率及3.5倍轴频为主,并且在啮频和3.5倍轴频附近存在大量的边频。SFD主要抑制的是低频区域3.5倍频附近的振动幅值。通过增加SFD,在支承2处低频区域的振幅从38g左 右降低到9.8g左右。SFD对低频3.5倍频附 近的振动幅值抑制效果明显,主要原因是SFD油膜反力为齿轮轴振动位移(x(t),y(t))和速度(x'(t),y'(t))的函数,而齿轮轴的振动位移和速度与轴的转动频率密切相关。
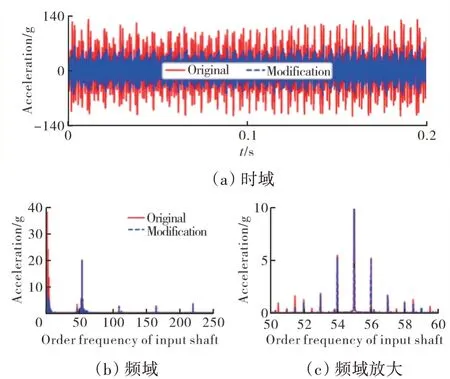
图14 转速为13400 r/min时支承2处的振动加速度
转速为1000~16000 r/min的升速过程中,弧齿锥齿轮齿面优化前后系统在支承2处的振动加速度均方根值如图15所示。从图中可见,在中高转速8000~16000 r/min,SFD对在支承2处的振动加速度有明显的抑制作用,各峰值处的振幅都有明显的减小,这一结果与转速为8000 r/min工况和高转速为13400 r/min工况的分析结果一致。
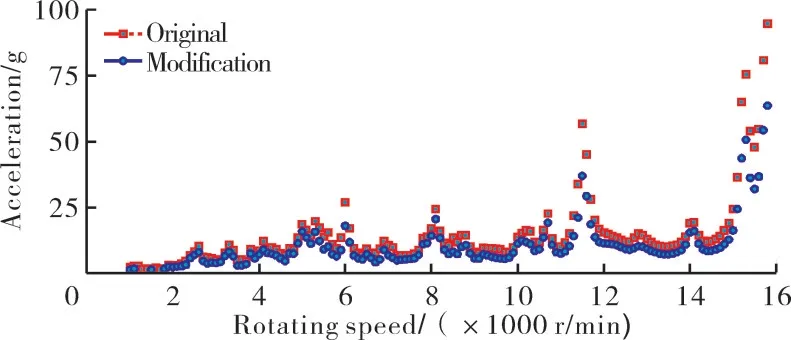
图15 升速工况时支承2处的振动加速度
4 原理性试验验证
搭建SFD支承下的弧齿锥齿轮系统试验台,验证弧齿锥齿轮系统动力学建模及理论分析方法的有效性。试验台结构如图16所示,大齿轮轴靠近齿轮端的一端由鼠笼型弹性支承和4点接触球轴承串联,然后与SFD并联支承,另一端为圆柱滚子轴承支承。小齿轮轴一端由4点角接触球轴承支承,另一端由圆柱滚子轴承支承。
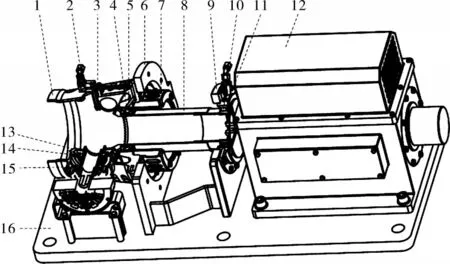
图16 含弹性支承的弧齿锥齿轮试验台结构
实测试验台轴承附近处的振动加速度并与理论计算结果进行对比,转速为13400 r/min时实测振动信号与理论振动信号频率成分对比如图17所示。理论和实际振动前6阶啮合频率的幅值基本吻合,振动幅值在同一量级,最大振幅出现在第1阶啮合频率上,这也与噪声信号的结果一致。理论分析在啮合频率处的振幅为19.7g,实测振动信号的振幅为16.9g,幅值大小基本吻合。此外,4倍啮频外的其余倍频成分的幅值也基本一致,主要区别是振动信号在1/3fm和1/2fm等次谐波分量在理论结果中未被激励出来。同样,转速为12315 r/min时实测振动信号与理论振动信号如图18所示。最大频率成分为第1阶啮合频率,理论与实际振幅有一定出入,但处于同一量级,在转速为12315 r/min时实际振动幅值为16g,理论振幅为27.5g,可以采用理论分析预测齿轮系统的振动响应。

图17 转速为13400 r/min时实测振动信号与理论振动信号啮合频率成分对比
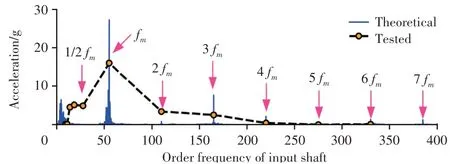
图18 12315 r/min时实测振动信号与理论振动信号啮合频率成分对比
为更充分地验证理论分析的有效性,实测转速为9200~14700 r/min升速过程中支承2处的振动加速度,实测和理论分析结果如图19所示。在整个转速范围内,理论分析结果与实测结果的吻合度较高,在振动峰值外二者幅值基本接近,并且都是在10200 r/min和11600 r/min附近达到峰值。由于在理论分析时未考虑激励载荷波动、负载波动以及增速器的齿轮副啮合激励等因素,相比实测振动信号,理论振动信号在转速为13600 r/min附近处的振动峰值未被激励出来。
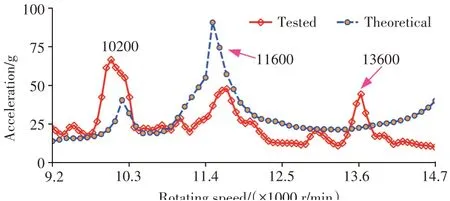
图19 转速为9200~14700 r/min时实测振动信号与理论分析振动信号对比
实测振动信号与理论振动信号对比表明,采用的弧齿锥齿轮系统动力学建模和理论分析方法可以较为准确地预测锥齿轮-SFD系统的振动响应,在前6阶啮合频率分量上的幅值相差不大,处于同一量级。实际数据与理论结果的主要差异主要体现在啮合频率的次谐波分量上,实测信号的次谐波频率成分在理论信号中未被激励出来,原因主要在于理论分析模型设置了多项假设,没有考虑很多非线性因素,如滚动轴承的非线性时变刚度、齿轮副时变齿侧间隙、齿轮副啮合油膜刚度等因素。
5 结论
(1)试验台中锥齿轮副的静态传动误差频率成分主要由大齿轮第1阶轴频fs1、小齿轮第1阶轴频fs2及其边频成分组成,在中高频区间还有小幅值的第1阶啮合频率成分fm及其边频成分。齿轮系统在支承处的振动主要由低频轴频的倍频及齿轮副啮合频率的倍频成分组成,包括3.5fs、fm、2fm、3fm、4fm、6fm及7fm等频率成分。振动频率成分中啮频、啮频的倍频及其边频主要由齿轮传动误差中的啮频和大小齿轮轴频调制激励出来。振动中的低频成分3.5fs主要由主、从动轮的轴频调制引起。在高转速8000~16000 r/min,SFD对在支承2处的振动加速度有明显抑制作用,各峰值处的振幅都有明显的减小。
(2)实测噪声信号和理论振动信号主要由2个频率带组成,在高频区域主要由第1阶啮合频率及轴频调制频率为主,在低频区域主要由4倍轴频及边频带组成,振动和噪声最大频率成分均为第1阶啮合频率。实测振动、噪声信号与理论振动信号在前6阶啮合频率成分幅值吻合度较高,振动幅值处于同一量级且趋势基本一致,验证了理论分析模型及分析方法的有效性。差异在于理论分析模型未考虑滚动轴承的非线性时变刚度、时变齿侧间隙、齿轮副啮合油膜刚度等因素,使得实测振动信号的次谐波频率成分(1/6fm、1/2fm)在理论振动信号中未被激励出来。

