汽流激振力下转子裂纹-碰摩振动故障研究

瓮 雷，向智玮

（1.91404部队，河北 秦皇岛 066000；2.91910部队，辽宁 大连 116000）

1 引言

转子作为军用航空发动机、舰用蒸汽轮机和燃气轮机等旋转机械的重要组成部件，工作在高温高压、交变载荷和易腐蚀的恶劣环境中，经常会由于各种原因逐渐形成疲劳裂纹，甚至发生部件碰摩导致设备运行振动幅值加大[1]。

而舰船蒸汽动力作为我军大型舰船的主要动力之一，在运行过程中经常会有故障发生。某型舰船机组设备出现严重的振动超标问题，如图1所示。经过拆卸汽轮机相关部件发现，汽轮机转子在运行过程中发生裂纹扩展，进而造成转子叶片断裂脱落，如图1（a）所示；并且由于转子轴承的推力块磨损和汽轮机辅推力轴承的板簧变形等原因，造成了系统轴瓦由于间隙过大，在下轴瓦工作面底部约60°范围内呈现出烧损现象，如图1（b）所示。

转子碰摩故障是旋转机械中常见的故障之一，如图1（b）所示，汽轮机转子在运行期间由于转子轴承的推力块磨损出现碰摩故障，导致转子轴瓦烧损。在转子的制造和安装过程中，由于设计误差或者安装误差的存在而引起转子部件的间隙不足等问题，进而引起碰摩。另外含有裂纹的轴系，也会因为轴刚度减小造成转子振动幅值变大，从而发生碰摩；同时转子发生碰摩故障时，也会造成转轴运行条件变得恶劣，在高温、高压、腐蚀和交变载荷下产生疲劳裂纹。因此，工程实际中转子故障并不是单一出现的，而是多种故障并存，相互之间耦合存在的，且振动故障问题都是非线性的。很多学者针对上面提到的转子裂纹或碰摩故障问题进行了研究，并得到了一些有价值的理论成果。文献[2]在考虑转子系统具有初始弯曲的基础上，建立并分析研究了具有裂纹和碰摩的转子模型的非线性动力学特性。刘民杰等人研究了碰摩故障下高维转子系统的降维方法，并进行了数值仿真分析。巩晓赟等人采用小波包能量谱分析研究了转静碰摩故障振动响应问题。文献[5]提出了一种基于融合信息熵距的振动诊断方法，并进一步在实验台上对裂纹-碰摩转子故障系统进行了实验研究。文献[6]建立了含有横向裂纹、转静碰摩的非线性转子模型，研究了不同转速下裂纹、碰摩单一故障下转子系统的振动响应，进一步研究了两种故障耦合情况下的振动响应特征。文献[7]研究了多自由度转子系统含有碰摩和裂纹故障的非线性动力学特性。

图1 某型舰用汽轮机故障现象Fig.1 The Fault of a Marine Steam Turbine

对于汽轮机机组来说，除了承受着重力、偏心力、非线性油膜力等各种非线性激励外，还承受着由于叶轮偏心引起的转子轴心上的非线性汽流激振力[8-9]。相关研究[10-11]表明这个非线性汽流激振力会使得转子系统失稳，而在这个汽轮机非线性间隙汽流激振力作用下转子系统的非线性振动问题却很少有人研究。因此，针对汽轮机激振力引起的转静件碰摩及裂纹耦合故障问题，建立了系统分析模型，并采用数值分析方法对分析模型进行了研究。

2 转子裂纹-碰摩故障动力学模型

针对所研究问题，只考虑转子的横向振动问题，建立转子分析模型，如图2所示。转子的两端有两个滑动轴承支承，且转子圆盘处的偏心量为e。采用精度和收敛性都比较好的Capone油膜力模型[1]，转子分析模型相关参数，如表1所示。

图2 转子系统分析模型Fig.2 The Analysis Model of Rotor System

表1 转子模型参数Tab.1 The Parameters of Rotor Model

2.1 汽轮机汽流激振力模型

当考虑转子汽流激振力时，系统的受力图，如图3所示。汽流激振力F a分解在x、y方向上分别为f a x、f ay。非线性汽流激振力无量纲形式为[9]：

图3 系统受力图Fig.3 Loading Diagram of System

2.2 汽轮机转子碰摩力模型

图4 转子碰摩力模型Fig.4 The Model of Rubbing Force

当发生碰摩时，在接触面上会生成一个法向力F n和相对运动的切向力Fτ，如图3所示。F n和Fτ可表示为[2]：

由以上可得到碰摩力为[2]：

2.3 系统运动微分方程

转子裂纹轴刚度模型采用文献[11]中模型，进而推导得到汽流激振力作用下转子分析模型的无量纲化运动方程为：

3 仿真结果及分析研究

采用四阶龙格库塔方法对转子运动方程（6）进行求解，进而研究转子系统的非线性动力学特性。系统的参数如下：m1=4.0kg，m2=32.1kg，R=25mm，L=12mm，μ=0.018Pa·s，c1=1050N·s∕m、c2=2100N·s∕m、k=2.5×107N∕m，k c=3.6×107N∕m，b=0.11mm，f=0.1，δ=0.12mm，ρ0=11.8kg∕m3，R T=0.5m，R B=0.37m，β1=35°，β2=40°，ς=0.83，δ=1.2×10-3m，V=200m∕s。系统一阶临界转速为ω0=882.5rad∕s。

3.1 激振力作用下碰摩故障系统研究

汽轮机转子系统在运行过程中，由于工作环境的复杂性，承受着多重非线性因素的影响，特别是在转子碰摩故障发生时，这些因素的存在会进一步加剧机组的振动甚至失稳，对机组的运行造成很大的安全隐患。因此，研究分析在不同激励因素作用下的响应，为进一步了解系统的动力学特征以及实际故障诊断提供理论基础。

转子在不同激励情况下响应分岔图，如图5所示。图5（a）为只考虑油膜力和偏心力时转子响应分岔图，系统的响应状态先后经历周期1运动、短暂的混沌、周期2、周期5以及在高速区的复杂运动。图5（b）为考虑汽轮机激振力作用时系统的响应分岔图，与图5（a）对比可以看出，由于激振力的作用，系统的亚临界转速短暂的混沌运动消失，且转速较低时激振力对系统的影响比较小；当转速进一步的增加，激振力对系统才有比较明显的影响，主要体现在系统响应在临界转速附近的分叉图由一条自相似轨迹演变为两条，且混沌区域明显减小；转速ω=955rad∕s时系统的响应，系统的Poincaré截面上的混沌小岛由一个演变为两个，且由于激振力的作用，响应图上1∕2频谱幅值明显大于工频，如图6（a）、图6（b）所示。图5（c）是在图5（a）的基础上考虑碰摩时的响应图，由于碰摩故障的存在，系统的响应受到了明显的影响，转速较低时受碰摩故障影响较小；如图6（c）所示，由于碰摩力的作用在ω=955rad∕s时系统响应的Poincaré截面上混沌小岛由一个演变成两个；并且在超临界转速附近碰摩力使得之前响应的周期2和周期5运动消失。

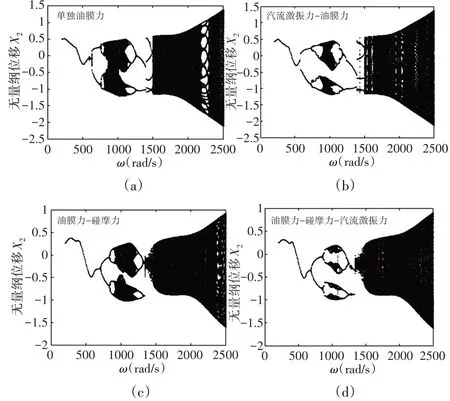
图5转子系统响应的分岔图Fig.5 Bifurcation Diagram of the System with the Change ofω

图5 （d）为进一步考虑激振力时系统的响应。图5（d）与图5（a）～图5（c）可以明显看出，综合考虑多种非线性因素的耦合作用后，碰摩故障转子系统响应的分岔图发生了复杂的变化，混沌区域明显减小，且频谱图上出现明显幅值较大的1∕4倍频、3∕4倍频；从图6（d）可以看出，系统的Poincaré截面上演变为四个孤立的混沌小岛。

图6ω=955rad∕s时响应的Poincaré图和频谱图Fig.6 The PoincaréMap and Frequency Spectrums of Rotor System whenω=955rad∕s

3.2 裂纹深度对碰摩转子系统的影响

图7 （a）～图7（c）分析了在激振力作用下，无量纲裂纹深度a∕R分别为0.3、0.7和1.0时系统响应的分岔图。通过与图5（d）在激振力作用下单一碰摩故障转子的响应对比，可以进一步了解裂纹对激振力作用下转子耦合系统的动力学特性。

图7 不同无量纲裂纹深度下转子系统的分岔图Fig.7 Bifurcation Diagram of Rotor System on Different Depths of Crack

当a∕R=0.3时，如图7（a）所示。与图5（d）对比并无很大的变化，说明较小的裂纹对系统的并没有太大的影响。当a∕R=0.7时，在临界转速附近之前表现为混沌的区域变窄，如图7（b）所示；且在超临界转速区域，之前表现为拟周期运动的区域中出现多倍周期运动，在Poincaré截面上表现为多个离散的点，且频谱图上主要体现为3∕4和2倍频，如图8（a）所示。随着裂纹深度的进一步增大到a∕R=1.0时，裂纹对临界转速及超临界转速区域的影响比较大，主要表现为临界转速附近的混沌进一步明显变窄，如图7（c）所示；在超临界转速区域1670rad∕s≤ω≤1945rad∕s存在较长的周期3运动，如图8（b）所示为ω=1755rad∕s时响应的Poincaré截面为三个离散的点。上述分析可以看出，由于裂纹的存在，使得转轴刚度随着裂纹深度的变化而不断变化，使得激振力作用下的耦合转子系统表现出更为复杂的非线性特性。

图8 ω=1755rad∕s，不同裂纹深度下Poincaré截面图和频谱图Fig.8 The PoincaréMap and Frequency Spectrums of Rotor System on Different Depths of Crack Whenω=1755rad∕s

4 结论

通过分析现有文献中研究存在的不足，综合考虑转轴偏心量、非稳态油膜力和汽轮机非线性汽流激振力作用，针对汽轮机激振力引起的转静件碰摩及裂纹耦合故障问题，建立了系统分析模型，并采用数值分析方法研究分析在不同激励因素作用下的响应，为进一步了解系统的动力学特征以及实际故障诊断提供理论基础。得出如下结论：（1）在综合考虑汽流激振力作用下多种非线性因素作用时，碰摩转子系统在临界转速的混沌区域明显减小，并出现有幅值较大的1∕4、3∕4倍频。（2）由于裂纹的存在，使得转轴刚度随着裂纹深度的变化而不断变化，使得激振力作用下的耦合转子系统表现出更为复杂的非线性特性。当裂纹深度增加时，故障转子系统的混沌区域逐渐减小；在超临界转速区域系统响应呈现出较长的周期3运动，频谱图上主要体现为3∕4、2倍频。