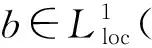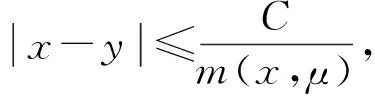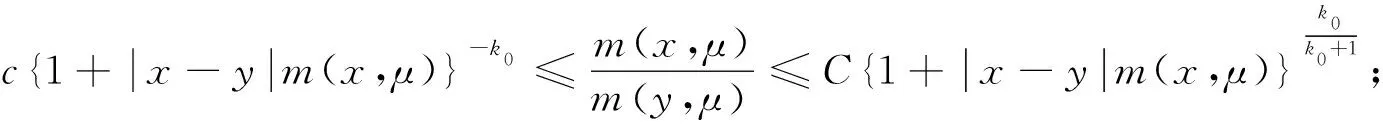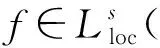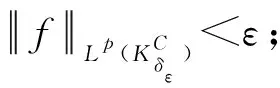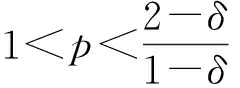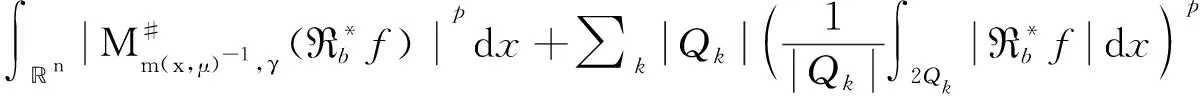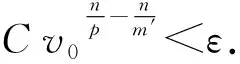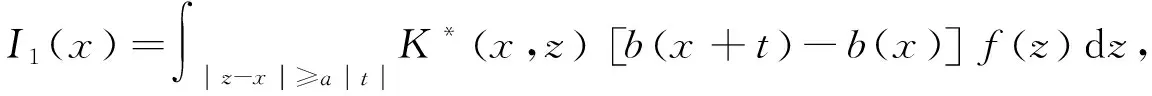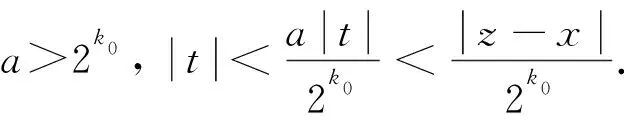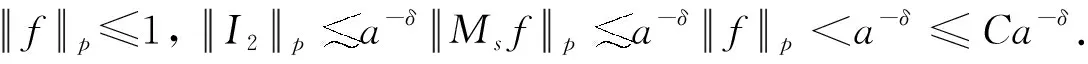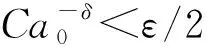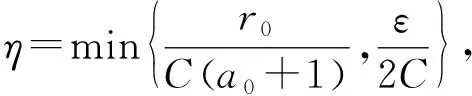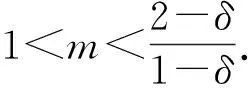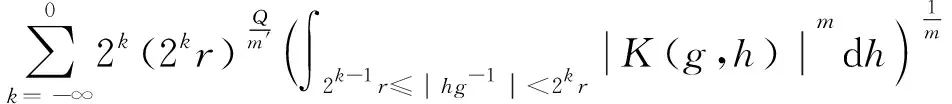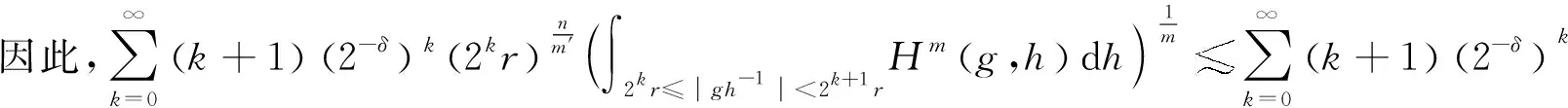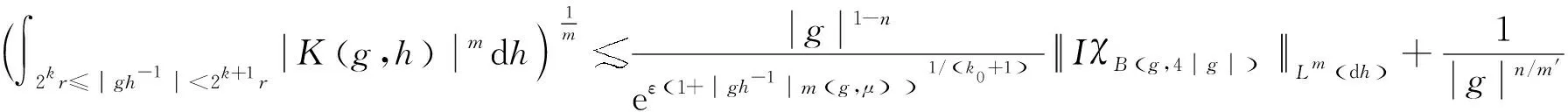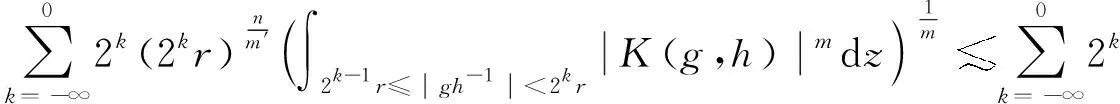与广义薛定谔算子相关的利兹变换及其交换子的Lp紧性

丁姗姗

(中国人民解放军陆军特种作战学院，510500，广东省广州市)

0 引 言

在泛函分析理论中，紧算子是一类重要的分支.令L是从巴拿赫空间X映射到另一个巴拿赫空间Y的线性算子，如果X中任意一个有界子集在L下的像都是Y中的相对紧子集，则L是紧算子.关于紧算子的一个经典例子是索伯列夫嵌入定理.通过这样的嵌入，可以将椭圆有界性问题转化为Fredholm积分方程.关于紧算子的更多研究，可以参考文献[1-3].

设T是一个卷积奇异积分算子.1978年，Uchiyama在文献[4]中给出了交换子[b,T]的有界性和紧性，并证明了对于1

根据文献[7]和[8]，在本文中，始终假设μ满足以下条件：存在正常数C0、C1和δ使得对于0

(1)

μ(B(x,2r))≤C1{μ(B(x,r))+rn-2}，

(2)

其中B(x,r)表示以x为圆心，以r为半径的开球.由文献[8]知，(1)式等价于

实际上，(1)式可以认为是尺度不变的Kato条件，(2)式意味着测度μ可以使球加倍，并满足μ(B(x,r))≥Crn-2.申在文献[7，8]中指出：如果dμ=V(x)dx，并且V(x)是非负位势，满足

即V(x)属于逆赫尔德类，则测度μ满足(1)，(2).

其中C1是(2)中的常数.

其中γ：[0,1]→n是绝对连续的，并且满足γ(0)=x，γ(1)=y.

1 相关性质及引理

2n+1维的海森堡群n是一个具有基本流行2n×的幂零李群.群结构为

所有非平凡交换关系形式[Xj,Xn+j]=-4X2n+1，j=1,2,…n.

次调和算子Δ和梯度∇分别定义为

|g|=(|x|4+|t|2)1/4，g=(x,t)∈n.

令d(g,h)=|g-1h|，则以g为圆心，r为半径的球定义为

B(g,r)={h∈n,|g-1h|

性质1 假设μ满足(1)和(2)，则

(a)对于任意x∈n，有0

(b)如果r=m(x,μ)-1，则rn-2≤μ(B(x,r))≤C1rn-2；

引理1 设μ满足(1)和(2)，δ∈(0,1)，则当s>2-δ，存在常数C，使得

引理2 (Frechet-Kolmogorov) 对于1≤p<∞，Lp(n)的子集G是强预紧的当且仅当：

引理3 设μ是n，n≥3上的非负拉东测度且满足(1)，(2)，δ∈(0,1)，则

本文将在第2、3节中分别证明与广义薛定谔算子相关的利兹变换及其对偶变换[b,T]在n和n上的紧性. 为了简化叙述，将利用ab表示a≤Cb.

定理1 设μ是n，n≥3上的非负拉东测度且满足(1)和(2)，δ∈(0,1)，m>1，b∈VMO(n).

由引理2知，要证[b,T]的紧性，只需证明[b,T]满足下述3个条件：

定理1的证明先证明第2个结论. 根据对偶性可以同样证明出第1个结论.

Ⅰ. 由引理1知若f∈Lp(n)，p>2-δ，则n). 当2-δ

对于上式的第一部分，如果令f=f1+f2，其中f1=fχ2B，则

Ⅲ. 对于任意x,z∈n，a>2k0，

对于任意整数k≥0，记bk=B(x,2ka|t|)，Ck=B(x+t,2k(a+1)|t|).

再估计I3(x).对于任意满足|z-x|

根据引理3，由赫尔德不等式有

最后估计I4(x).因为a|t|<(a+1)|t|

对Ii(x)，(i=1,2,3,4)的估计意味着对任意ε>0，存在正常数a0和C，使得若(a0+1)|t|

假设p≥1，R在Lp(n)上有界，K(g,h)为R的核函数.令H(g,h)表示(n×n){g=h}上的非负局部可积函数，如果存在δ>0和整数k0>0，使得对于有

则称H(g,h)是核函数K(g,h)的控制函数.

1)H1(m)：存在K(g,h)的控制函数H(g,h)使得

2)H2(m)：存在N≥1使得对于任意v,R>N，g∈n且|g|>vR，有

3)H3(m)：存在r0>0使得对于任意0

实际上，H1(m)表示有界性条件，H2(m)表示局部Lp条件，H3(m)表示一致收敛条件.如果R的核函数满足上述3个条件，则R是紧的.因此上述条件又称为紧性条件.

引理4[6]定理3.8假设μ满足(1)和(2)，δ∈(0,1)， 当2-δ

定理2 设μ是n，n≥3上的非负拉东测度且满足(1)和(2)，δ∈(0,1).如果K(g,h)满足Hi(m)，i=1,2,3，则与广义薛定谔算子相关的利兹变换R在Lp(n)上是紧的.

证明由与广义薛定谔算子相关的利兹变换的有界性及引理4知，要证明R在Lp(n)上的紧性，只需证K(g,h)满足定义2中的紧性条件.

首先，证明K(g,h)满足H1(m).对于K(g,h)，存在控制函数

选择N0>log2C1+1，固定N=N0，则对于任意r>0，任意整数k，当|gh-1|<2k+1r，|uh-1|<|hg-1|时，有|gu-1|<2k+3r.根据Minkowski不等式和性质2有

其次，证明K(g,h)满足H2(m).对于任意v，R>2，g，h∈n，|g|>vR，|h|

根据Minkowski不等式和性质2有

最后，相似地，对于任意r>0有

所以K(x,y)满足H3(m).