不完全量测下基于信息一致性的分布式容积卡尔曼滤波算法

王宁，李银伢，戚国庆，盛安冬

(南京理工大学 自动化学院，江苏 南京 210094)

0 引言

现代火控系统主要包含目标搜索识别、跟踪、命中和毁伤4个重要环节，其中目标跟踪是后续武器系统命中和毁伤目标的必要前提[1]。因此，实时、准确、稳定地获取目标的运动状态是火控系统信息处理领域中重要的研究课题之一。

随着传统空中目标的机动性能、隐身性能的提高，以及制导炸弹、巡航导弹和无人机等新型飞行器在现代战场上的大量应用，使得单一传感器的估计性能难以满足新形势、新技术条件下的目标跟踪作战需求[2-3]。另一方面，网络通讯和智能传感器的飞速发展为多传感器信息融合提供了技术支持，这使得网络化的目标跟踪系统被广泛应用于现代火控系统中，其中分布式跟踪系统更是由于通信量小、可靠性高等优势受到了越来越多的关注和研究[4]。

在实际应用中，分布式火控网络中各个作战单元需要协调一致地对目标进行跟踪、打击，以获得最佳的综合毁伤效果。因此，分布式火控网络需要避免部分探测单元由于自身估计精度太低而造成目标漏网现象，这就要求分布式跟踪系统在提高各探测单元估计精度的同时保持估计状态的一致性。此外，在实际应用中，由于目标的隐身性、高机动性，设备自身的偶发故障，以及真实战场上电子对抗干扰等诸多因素，使得探测单元对目标的探测概率小于1，即出现不完全量测现象[5]。不完全量测下跟踪系统的估计性能往往随着探测概率的下降而降低，特别是当探测概率小于跟踪系统临界探测概率时，跟踪系统统计意义下的估计误差方差会发散[6]。因此，将一致性估计算法应用于分布式跟踪系统，并且在不完全量测下提高其估计精度、保证算法收敛性，对分布式火控系统目标跟踪理论研究和工程应用都有着重要的现实意义。

在现有的一致性滤波算法中，基于信息一致性的分布式滤波算法由Battistelli等首先提出，该方法保证了估计结果即使在一步内也可以实现稳定[7]。这一特征引起了学者们的广泛关注：Li等[8]提出了平均一致性无迹卡尔曼滤波(UKF)算法；Wei等[9]提出了基于协方差交叉方法的线性一致性滤波算法。考虑到一致性估计算法中可能存在的不完全量测情形，Li等[10]提出了一种不完全量测下的线性一致性估计算法；Xu等[11]提出了存在通信丢包情况的二级线性一致性卡尔曼滤波算法；陈烨等[12]提出了基于事件触发机制的不完全量测线性一致性估计算法。然而，在不完全量测下，非线性系统的一致性估计问题及其对应算法估计方差的收敛性问题还鲜有相关研究成果发表。

基于以上分析，考虑实际应用中存在的不完全量测情形，本文提出了一种基于信息一致性的分布式容积卡尔曼滤波(ICDCKF)算法。该算法考虑了各探测单元量测信息的相关性，将协方差交叉方法应用于一致性融合系数的计算，提高了互协方差未知条件下分布式融合算法的估计精度。进一步地，本文给出了不完全量测下，ICDCKF算法估计误差方差有界的条件，并通过数值算例对理论成果进行分析验证。ICDCKF算法应用于一类光电跟踪网络，对两种典型运动目标进行了跟踪仿真和对比分析，验证了所提算法的有效性和可行性。

1 问题描述

在笛卡尔坐标系下，考虑一类非线性运动目标的动态方程描述如下：

xk=f(xk-1)+wk-1,

(1)

(2)

(3)

式中：P{·}为某一事件的发生概率；λi∈[0,1]为探测单元i成功测量目标的概率。

培养学生的求知欲望和解决实际问题的能力往往需从问题开始；学习的过程更是一个不断发现问题、分析问题和解决问题的过程。启发式教学可以调动学生学习的积极主动性；让学生独立思考，锻炼逻辑思维能力；培养学生的动手能力、观察能力、分析问题和解决问题的能力。

在本文考虑的跟踪网络中，每一个探测单元不仅具有对目标状态的量测功能，还具备一定的通信和计算能力，可以完成对目标的状态估计和信息融合任务，如图1所示。图1中，各探测单元均以相同的探测、通信以及估计频率对目标进行跟踪，且相邻探测单元之间可以进行局部估计的信息交互。该探测网络中的探测设备以光电探测仪、近程火控跟踪雷达为主，探测单元之间通过有线或无线通信方式实现探测网络的构建及信息交互，可用于要地末端防御中的防空目标探测跟踪领域。

图1 分布式跟踪网络结构图

证明根据所提算法的第3步可知：

基于图1所示的分布式跟踪网络，已有诸多算法可以基本完成目标跟踪任务，但针对不完全量测条件下的非线性运动目标，仍有以下问题值得深入研究：如何设计一种新型分布式非线性融合算法以获取针对非线性目标的一致性高精度状态估计结果？如何保证不完全量测情形下所提算法估计结果的收敛性？并从理论上给出算法估计误差方差有界性的严格证明？后文将就这些问题进行详尽阐述。

2 基于信息一致性的分布式容积卡尔曼滤波算法

针对第1节所描述的非线性目标跟踪系统(1)式和(2)式，为获得分布式跟踪网络中针对非线性目标的一致性状态估计结果，本节给出一种ICDCKF算法。该算法本质上属于一类分布式估计算法，因此各探测单元需要首先完成对目标状态的局部估计，然后通过与相邻单元之间的信息交互，最终完成一致性融合估计。

以探测单元i为例，考虑实际应用中存在的不完全量测现象，参考文献[13]中所提算法，首先给出一种改进的容积卡尔曼滤波(MCKF)算法用于目标状态的局部估计，如算法1所示。

算法1MCKF算法。

1)时间更新

锄禾火锅主料有牛肉片、鸡片、虾片、鱼片、猪排肉、猪腰片以及明虾等，配料有粉丝、鱼丸、菠菜、白菜、洋菜和色拉油等，吃法比较像中国的炒菜：食用时是先点燃平底锅，等油烧热时将菠菜和洋葱等放入锅中拌炒至八成熟，再放入白菜梗同炒，加白糖和酱油，待全部炒熟后再把自已喜爱的各式主料加放到锅中煎熟，一边食用一边煎煮，吃到一半时，再加入一些鲜汤煮熟，加佐料后再在鲜汤内涮以主料食用之。

(4)

依据其分解结果，可以计算容积点为

MRI平扫检出率高于多排螺旋CT平扫，P＜0.05；两种检测方式增强扫描检出率对比无明显差异，P＞0.05。如下表所示。

(5)

则有(14)式成立：

由此，可以获得目标状态的先验估计值及先验估计方差为

(6)

2)量测更新

对先验估计方差进行Cholesky分解：

基于LabWindows/CVI的某型综合控制单元测试设备开发………………………………郝云虎，李 强，张贤周(3)

(7)

可得相应的容积点如下：

(8)

(9)

(10)

和

(11)

(12)

上式中Y为被解释变量，X为解释变量，i为样本个数，随机扰动项μ代表着那些对Y有影响但又未纳入模型的诸多因素的综合影响。为了使对模型的估计具有良好的统计性质，对无法直接观测的随机扰动项的分布，需要进行以下一些基本假定：

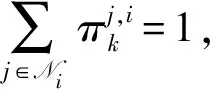
(13)

另外，工作坊虽然可以为学生提供自主学习、探索创新的平台，其不仅需要从教学方法上进行探讨，还要从硬件环境上予以保证[12]：学校要为工作坊提供充足的工作空间、设备、材料和制度支持等，如：建立完善的校内专业实训室并坚持对学生开放，选聘优秀的实训教师，鼓励学生申报科研项目、实践训练项目和创新项目，做好管理工作等，保证工作坊的健康、可持续发展。

证明由于算法的估计结果呈高斯分布，记

案例1：学生到学校生物园观察植物，回到教室后遭到了教师的质问：为什么要到那儿去？教师的本意是让学生明白，我们身边到处都有可供观察的植物，但是他的质问已构成了对学生自主行为的一种干预，这或许是教师权威主义的瞬间行为。

(14)

进一步地，将不同单元j∈Ni代入(14)式并相乘：

在可可西里的一周里，温衡去了传说中的无人区，去了巴颜喀拉山顶看日出，走的那天她才打开手机，陶小西没有再发来任何消息，她最后一点希冀也破灭了。

(15)

(13)式代入(15)式，可以得到

(16)

引理1得证。

根据引理1可知，利用(13)式可以求得无偏的融合估计结果，但在现有的一些基于信息一致性的融合算法中，通常采用最大度权重方法和Metropolis权重方法求取一致性融合系数[16-17]。这些方法只考虑了跟踪网络的拓扑结构，并没有考虑各探测单元的局部估计信息精度和相互之间估计信息的相关性。事实上，跟踪网络中各探测单元的局部估计通常是相关的[18]，因此在融合过程中需要充分考虑各探测单元局部估计信息的相关性。不过在实际应用过程中，由于各探测单元估计值之间的互协方差通常难以求取或求取的计算量较大，通常无法获取各探测单元局部估计误差的互协方差。因此，本文引入协方差交叉方法，用以解决各探测单元之间互协方差未知的问题[19]。通常，协方差交叉算法表述如下：

(17)

(18)

该优化问题是一个N维非线性优化问题，可以由MATLAB软件通用优化函数“fmincon”求解。

针对本文研究的不完全量测条件下非线性系统的分布式跟踪问题，借鉴协方差交叉方法在解决互协方差未知情况时状态估计问题的精度优势，将该方法用于一致性算法的融合系数求取，进而给出k时刻的ICDCKF算法，如算法2所示。

算法2ICDCKF算法。

需要说明的是，针对非线性目标跟踪系统，常用的滤波方法有扩展卡尔曼滤波(EKF)、UKF、容积卡尔曼滤波(CKF)、粒子滤波(PF)等。相关研究表明，CKF算法在高维非线性系统中的估计精度和稳定性优于EKF和UKF[14]，更适合用于实际的目标跟踪系统。另一方面，由于研究的非线性系统为高斯白噪声，PF算法在处理非高斯噪声方面的优势无法体现，且相对CKF算法，其运算复杂度更高[15]，难以适应实时性要求较高的目标跟踪系统。综上所述，本文采用CKF算法对目标进行状态滤波。

3)探测单元i接收探测单元j(j∈Nii)的局部估计信息，并按(19)式完成一致性融合计算：

(19)

式中：I为适维单位矩阵。

(20)

3 不完全量测下ICDCKF算法的稳定性分析

估计方差是否有界是判定一个算法能否有效应用的重要标准。尤其对于非线性系统和不完全量测情形，估计方差是否有界直接决定了所提算法能否有效、可行地对目标状态进行估计。针对这一问题，本节对不完全量测下所提ICDCKF算法的稳定性进行深入分析，并给出确保估计方差有界的条件。

(21)

利用伪线性化方法对(21)式进行线性化处理[20]，可得

近年来，随着标准化事业的蓬勃发展，标准学研究与实践不断深入，新的理论与方法不断涌现，标准化学科的领域不断拓展、内涵日益丰富。当前，国内外对于标准化基本理论的研究发展迅速，除了传统经济学、管理学以外，法学、社会学、公共治理理论、产业创新理论、网络经济学等领域全面介入，对标准、标准化的内涵和外延开展跨学科研究，形成了标准化学科发展的新特点。为此，我们需要就标准化的基本概念进行重新认识与现代诠释。

(22)

考虑由N个探测单元组成的跟踪网络对上述目标状态进行量测，当存在不完全量测时，探测单元i的量测方程通常描述为

(23)

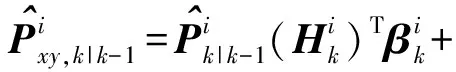
ΔPxz,k|k-1+δPxz,k|k-1,

(24)

(25)

在给出算法收敛性定理之前，首先给出必要的引理和假设。

(A+B)-1>A-1-A-1BA-1.

(26)

假设2初始估计误差方差有界。

我们对他们婚后的床上生涯就这样略知一二，我们对他们另外的生活知道得就更多了，总之我们都认为林孟艳福不浅，萍萍的漂亮是有目共睹的，她的温柔与勤快我们也都看在眼里，我们从来没有看到过她和林孟为了什么而争执起来。我们坐在他们家中时，她总是及时地为我们的茶杯斟上水，把火柴送到某一双准备点燃香烟的手中。而林孟，结婚以后的皮鞋总是锃亮锃亮的，衣着也越来越得体了，这当然是因为有了萍萍这样的一个妻子。在此之前，他是我们这些朋友中衣服穿得最糟糕的人。

基于上述分析及假设，可给出定理1如下。

2、表面平整，截面尺寸准确，梁的挠度变形及柱的垂直度符合相关规定。主要受力和连接部位无露筋、蜂窝、空洞、夹渣、疏松、明显裂缝、孔洞、腐蚀、虫蛀等现象。

为分析各年级加法减法速度的差异性，采用SNK方法，以P<0.05显著性差异为依据，根据组间及组内变异的具体情况将其分为5个等级，等级越高，代表口算时间越短，即速度越快，具体如表5所示．

(27)

为方便描述，跟踪网络的通信拓扑用无向图g=(N,ε)表示，其中N={1,2,…,N}为节点的集合，ε为边的集合。如果一条边(i,j)∈ε，则称探测单元j为探测单元i的邻居节点，且将探测单元i的邻居节点集合记为Ni.特别地，探测单元i属于自身的邻居，即i∈Ni.当所指集合Ni不包含探测单元i时，记作Nii.

增减翻译策略是常见的翻译技巧之一。然而，无论是增词还是减词，翻译范畴里强调的是，在不更改原文语义的基础上，为了更加符合目的语文本的语言系统规范，才可以考虑增词或减词。若减词使原文语义在译文中遭受缺损，不仅违背了忠实传达原文语义的翻译原则，对文学文本而言，还会降低文本欣赏的完整度，限制译文读者的联想空间。如：

(28)

(29)

对(29)式两边求逆，且该逆矩阵的迹为

(30)

(31)

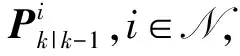
(32)

(33)

又由假设1，可以将(33)式进一步转化为

(34)

(35)

令

则不等式(35)式可以转换为

(36)

综上所述，定理1得证。

注1如果跟踪网络中存在部分节点没有探测能力，可假设该类节点的探测概率为λi=0，则在满足上述估计方差有界的条件时，本文所提ICDCKF算法仍可保证该类节点估计信息的有界性。因此，本文所提算法可推广应用于包含部分无探测能力节点的跟踪网络中。

4 数值算例

4.1 算例1

为说明不完全量测下ICDCKF的收敛性和定理1所给的估计方差有界条件的正确性，考虑一个由3个探测单元组成环形的跟踪网络对理论结果进行仿真验证。同时，为了与文献[13]所提单个探测单元滤波(CKFI)算法的估计方差进行对比，本文考虑与文献[13]中算例1相同的非线性系统：

(37)

仿真结果如图2所示。由图2可知：节点的探测概率越高，ICDCKF算法的估计精度越高；当探测概率为1时，可以取得最佳的估计精度；当λi>0.15时，CKFI算法的估计方差可以收敛；而对于基于分布式跟踪网络的ICDCKF算法而言，当探测概率λi>0.05时，估计方差即可实现收敛。

图2 不同探测概率下ICDCKF和CKFI估计误差方差

综上所述，两种算法的估计精度和探测概率均呈正相关关系，且在满足估计方差有界的情况下，本文所提ICDCKF算法相对于CKFI算法有更低的探测概率需求。另外，在数值仿真中，ICDCKF算法估计方差有界所需的条件验证了本文定理1所提理论的正确性。

4.2 算例2

为进一步验证本文所提算法的有效性和在实际应用中的可行性，将本文所提ICDCKF算法应用于一类光电跟踪网络，通过对不同运动模型下的目标进行跟踪仿真实验，对比不同探测概率下本文所提ICDCKF算法的估计精度，并将其与其他现有常见估计算法进行比较。

不失一般性，记目标状态为

式中：I3为三维单位向量；T为采样周期；q为噪声强度，q=1; ⊗为Kronecker积。

考虑由9个探测单元组成的分布式跟踪网络对三维目标进行跟踪。假设所有探测单元均分布于高度为0 km的水平面上，且以探测单元5的坐标为坐标原点，则该分布式跟踪网络的拓扑结构及探测单元坐标分布如图3所示。

图3 探测单元坐标水平投影及网络拓扑结构

在该跟踪网络中，记单个探测单元i的量测方程为

(38)

为了评估算法估计精度，分别定义位置均方根误差(RMSE)和速度RMSE如下：

进一步地，参考累积RMSE(ARMSE)的定义方法[23]，本文利用位置平均ARMSE(AARMSE)和速度AARMSE来评价滤波算法在跟踪网络中的整体估计性能，将其分别定义为

式中：K为目标航路的采样周期次数。

为比较不同算法在跟踪系统中状态估计的一致性，定义系统非一致估计值[24]为

在以下两种典型的目标运动模型(匀速圆周运动模型和再入段弹道目标运动模型)下进行200次蒙特卡洛仿真实验。

仿真场景1匀速圆周运动(CT)模型，运动半径为2 000 m，角速度ω=0.05 rad/s，航高为1 000 m.目标初始状态和状态转移函数分别为

x0=

[0 m -100 m/s 2 000 m 0 m/s 1 000 m 0 m/s]T,

f(xk)=

式中：T=0.5 s.该模型下的目标运动轨迹如图4所示。

图4 仿真场景1下目标运动轨迹

首先考虑探测概率为0.7的情况，将ICDCKF算法应用于如图3所示的跟踪网络中，并与CKFI算法、基于Metropolis权重的信息一致容积卡尔曼(KCF_Me)算法[17]和基于协方差交叉方法的容积卡尔曼融合(CKF_CI)算法[19]对比，可得如图5和图6所示部分探测单元融合结果的位置RMSE曲线和速度RMSE曲线。

图5 仿真场景1下探测概率为0.7时估计算法的位置RMSE对比

图6 仿真场景1下探测概率为0.7时估计算法的速度RMSE对比

由图5和图6可知，与CKFI算法和CKF_CI算法相比，本文所提ICDCKF算法和KCF_Me算法均有较高的估计精度和较好的一致性性能。在估计误差的收敛速度方面，ICDCKF算法可在t=6 s时达到稳定，而KCF_Me算法在t=10 s时才能稳定。因此，本文所提ICDCKF算法的收敛性更好，也使得该算法在实际应用中较其他算法更具实用性。

另一方面，该场景下不同算法的系统非一致估计值如图7所示。由图7可知，在估计结果稳定后，本文所提ICDCKF算法和KCF_Me算法在系统的状态估计一致性方面性能相似，但本文算法能够更快地达到状态估计的一致。

图7 仿真场景1下探测概率为0.7时估计算法的非一致估计值对比

针对估计算法在跟踪网络中的整体估计精度，这4种估计算法在不同探测概率条件下的AARMSE数据如表1所示。由表1可以看出：当探测概率为0.7时，ICDCKF算法的位置精度较CKFI算法、CKF_CI算法和KCF_Me算法分别提高了58.8%、30.8%和28.4%，速度精度分别提高了26.4%、17.2%和17.7%；当探测概率降低到0.3时，本文所提算法的位置精度较其他3种算法更是提高了63.0%、34.9%和45.0%，速度精度分别提高了27.9%、18.6%和23.1%.因此，本文所提算法较其他算法在估计精度上均有大幅提高，且在低探测概率条件下，本文所提算法的优势更加明显。

表1 仿真场景1下不同探测概率的估计算法AARMSE对比

仿真场景2再入段弹道目标运动(RBT)模型[25]，目标初始航速为200 m/s，初始航高为5 000 m，目标弹道系数β=4 000 kg/(m·s2)。目标初始状态和状态转移函数分别为

x0=[2 300 m -200 m/s 2 000 m

0 m/s 5 000 m 0 m/s]T,

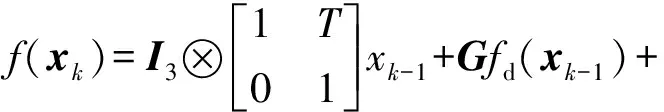
G[0 0 -g]T,

图8 仿真场景2下目标运动轨迹

类似地，对弹道目标再入段飞行轨迹进行跟踪，可以分别得到探测概率为0.7时不同估计算法的位置RMSE和速度RMSE变化趋势分别如图9和图10所示，系统非一致估计值对比如图11所示，以及不同探测概率时不同估计算法的AARMSE如表2所示。

表2 仿真场景2下不同探测概率的估计算法AARMSE对比

图9 仿真场景2下探测概率为0.7时估计算法的位置RMSE对比

图11 仿真场景2下探测概率为0.7时估计算法的非一致估计值对比

与CT模型相似，针对RBT模型的运动目标，本文所提ICDCKF算法分别在t=10 s和t=6 s时分别实现位置RMSE和速度RMSE的收敛，均早于其他算法。就系统状态估计一致性而言，本文算法达到系统估计状态一致的速度也略快于KCF_Me算法。在整体估计精度方面，当探测概率为0.7时，本文算法的位置精度较CKFI算法、CKF_CI算法和KCF_Me算法分别提高了60.3%、35.4%和32.2%，而速度精度也分别提高了17.7%、12.6%和13.3%.当探测概率由0.7下降到0.3时，本文算法的整体估计精度较其他算法也有大幅提高，且该算法的位置精度和速度精度较λi=0.7时分别损失46.7%和10.1%，与其他3种算法相比，精度损失也为最小。

综上所述，根据两种典型运动模型下的目标跟踪仿真，结果表明：在不完全量测条件下，无论目标的运动轨迹为线性时变模型(CT)还是非线性模型(RBT)，本文所提ICDCKF算法均可以得到一致性的估计结果，且与其他算法相比，本文算法的估计精度更高、收敛速度更快，在实际应用中具备可行性，是一种有效的非线性分布式一致性状态估计算法。

5 结论

在考虑实际应用中存在的不完全量测情形下，本文围绕分布式火控系统中的非线性目标跟踪问题展开了研究。得出如下主要结论：

1)提出了一种不完全量测下的ICDCKF算法。

2)从理论上证明了在不完全量测条件下，若系统探测概率大于一给定阈值，则所提ICDCKF算法的估计误差方差有界。

3)在一类光电跟踪网络中，通过两种典型运动模型下的目标跟踪实验，验证了所提算法的有效性和在实际应用中的可行性。

参考文献(References)

[1] 薄煜明，郭治，钱龙军，等.现代火控理论与应用基础[M].北京: 科学出版社，2012.

BO Y M，GUO Z，QIAN L J，et al.The theory of modern fire control system and its application basis[M].Beijing: Science Press，2012.(in Chinese)

[2] 王中许，张学彪，盛安冬.基于分布式节点的火控体系研究[J].兵工学报，2005，26(5):638-641.

WANG Z X，ZHANG X B，SHENG A D.Research on fire-control system based on distributed nodes[J].Acta Armamentarii，2005,26(5):638-641.(in Chinese)

[3] 陈晨，陈杰，张娟，等.网络化防空火控系统体系结构研究[J].兵工学报，2009，30(9):1253-1258.

CHEN C，CHEN J，ZHANG J，et al.Research on architecture of networked air defense fire control system[J].Acta Armamentarii，2009，30(9):1253-1258.(in Chinese)

[4] SUN S L，LIN H L，MA J，et al.Multi-sensor distributed fusion estimation with applications in networked systems: a review paper[J].Information Fusion，2017，38:122-134.

[5] SINOPOLI B，SCHENATO L，FRANSCESCHETTI L M，et al.Kalman filtering with intermittent observations[J].IEEE Transactions on Automatic Control，2004，49(9):1453-1464.

[6] 陈黎，王中许.不完全量测下光电跟踪系统中冗余测角信息的攫取研究[J].兵工学报，2011，32(7):819-826.

CHEN L，WANG Z X.Research on data mining of redundant angle information in optic-electric tracking system with intermittent observations[J].Acta Armamentarii，2011，32(7):819-826.(in Chinese)

[7] BATTISTELLI G，CHISCI L.Kullback-Leibler average，consensus on probability densities，and distributed state estimation with gua-ranteed stability[J].Automatica，2014，50(3): 707-718.

[8] LI W Y，WEI G L，HAN F，et al.Weighted average consensus-based unscented Kalman filtering[J].IEEE Transactions on Cybernetics，2017，46(2):558-567.

[9] WEI G L，LI W Y，DING D R，et al.Stability analysis of covariance intersection-based Kalman consensus filtering for time-varying systems[J].IEEE Transactions on Systems，Man and Cybernetics: Systems，2020，50(11): 4611-4622.

[10] LI W L，JIA Y M，DU J P.Distributed Kalman consensus filter with intermittent observations[J].Journal of the Franklin Institute，2015，352(9): 3764-3781.

[11] XU H X，BAI X Z，LIU P，et al.Hierarchical fusion estimation for WSNs with link failures based on Kalman-consensus filtering and covariance intersection[C]∥Proceedings of 39th Chinese Control Conference，.Shenyang，China: IEEE，2020: 5150-5154.

[12] 陈烨，盛安冬，戚国庆，等.不完全量测下事件触发卡尔曼一致滤波及在光电探测网中的应用[J].兵工学报，2018，39(4):625-634.

CHEN Y，SHENG A D，QI G Q，et al.Event-triggered Kalman consensus filter with intermittent measurements and its application to the electro-optical sensor network[J].Acta Armamentarii，2018，39(4):625-634.(in Chinese)

[13] SHI J，QI G Q，LI Y Y，et al.Stochastic convergence analysis of cubature Kalman filter with intermittent observations[J].Journal of Systems Engineering and Electronics，2018，29(4):823-833.

[14] 王小旭，潘泉，黄鹤，等.非线性系统确定采样型滤波算法综述[J].控制与决策.2012，27(6):801-812.

WANG X X，PAN Q，HUANG H，et al.Overview of deterministic sampling filtering algorithms for nonlinear system[J].Control and Decision，2012，27(6):801-812.(in Chinese)

[15] DAN S.Optimal state estimation: Kalman，H∞，and nonlinear approaches[M].Hoboken，NJ，US: John Wiley & Sons，Inc.，2006.

[16] XIAO L，BOYD S，LALL S.A scheme for robust distributed sensor fusion based on average consensus[C]∥ Proceedings of the 4th International Symposium on Information Processing in Sensor Networks.Boise，ID，US: IEEE，2005: 63-70.

[17] 丁自然，刘瑜，曲建跃，等.基于节点通信度的信息加权一致性滤波[J].系统工程与电子技术，2020，42(10): 2181-2188.

DING Z R，LIU Y，QU J Y，et al.Information weighted consensus filter algorithm based on node communication degree[J].Systems Engineering and Electronics，2020，42(10): 2181-2188.(in Chinese)

[18] RAN C J，DENG Z L.Robust fusion Kalman estimators for networked mixed uncertain systems with random one-step measurement delays，missing measurements，multiplicative noises and uncertain noise variances[J].Information Sciences，2020，534: 27-52.

[19] JULIER S J，UHLMAN J K.Handbook of multisensor data fusion[M].Boca Raton，FL，US: CRC Press，2009.

[20] XIONG K，ZHANG H Y，CHAN C W.Performance evaluation of UKF-based nonlinear filtering[J].Automatica，2006，42(2): 261-270.

[21] KLUGE S，REIF K，BROKATE M.Stochastic stability of the extended Kalman filter with intermittent observations[J].IEEE Transactions on Automatic Control，2010，55(2):514-518.

[22] BOUTAYEB M，AUBRY D.A strong tracking extended Kalman observer for nonlinear discrete-time systems[J].IEEE Transactions on Automatic Control，1999，44(8): 1550-1556.

[23] 穆静，蔡远利.迭代容积卡尔曼滤波算法及其应用[J].系统工程与电子技术，2011，33(7):1454-1457.

MU J，CAI Y L.Iterated cubature Kalman filter and its application[J].Systems Engineering and Electronics，2011，33(7):1454-1457.(in Chinese)

[24] 王帅，杨文，侍洪波.带丢包一致性滤波算法研究[J].自动化学报，2010，36(12): 1689-1696.

WANG S，YANG W，SHI H B.Consensus-based filtering algorithm with packet-dropping[J].Acta Automatica Sinica，2010，36(12): 1689-1696.(in Chinese)

[25] 巫春玲，韩崇昭.基于平方根求积卡尔曼滤波器的弹道目标跟踪[J].控制与决策，2010，25(5):721-724.

WU C L，HAN C Z.Tracking ballistic target based on square root quadrature Kalman filter[J].Control and Decision，2010，25(5):721-724.(in Chinese)