基于锈胀开裂寿命模型的钢筋保护层厚度研究

张 鑫 姚林芝

(1.青岛市李沧区开发建设推进中心，山东 青岛 266000； 2.青岛天华易境建筑设计有限公司，山东 青岛 266071)

0 引言

结构的耐久年限或使用寿命是指结构在正常使用或正常维护前提下，能够满足其预定功能的时间。进行结构耐久性评估最主要的是对结构使用寿命进行预测，而进行寿命预测的关键是了解结构的既定功能和失效准则。目前混凝土主要的失效准则，分为以下几类：碳化寿命准则，以保护层碳化到钢筋开始锈蚀的时间作为失效期限，如Funahashi E等；锈胀开裂寿命准则，以保护层外表面出现锈胀裂缝作为失效期限，如牛荻涛[1]；裂缝宽度与钢筋锈蚀量综合准则，以锈胀裂缝宽度或钢筋锈蚀量达到一定值作为失效期限，如刘西拉等[2]；承载力寿命准则，以结构承载力降低至某界限作为失效期限。

在不同的准则基础上，形成了概率法、经验法、模糊法、灰色理论法、动态分析法和神经网络法等寿命预测方法，本文采用概率法分析锈胀开裂寿命模型下，保护层厚度与可靠度的关系，并试探验证了规范中保护层设计厚度是否足够。

1 现行锈胀开裂寿命预测模型

国内外很多专家、学者针对保护层混凝土开裂时的耐久性寿命的预测模型进行了详细研究，列举以下几种：

1)牛荻涛预测模型[1]。

保护层混凝土开裂前的钢筋锈蚀深度计算模型：

δei(t)=Kcrλei(t-ti)

(1)

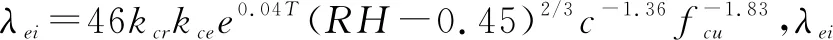
2)徐善华等[3]经过试验和检测拟合公式与前类似。

(2)

3)邸小坛预测模型[4]。

λ=β1β2β3(4.18/fcuk-0.073)×(1.85-0.04c)(5.18/d+0.13)t

(3)

其中，λ为钢筋截面损失率；β1,β2,β3分别为养护条件、水泥品种、环境作用修正系数；c和d分别为混凝土保护层厚度和钢筋直径。

4)电化学预测模型[5,6]。

由Faraday定律能求得钢筋的锈蚀质量ML和锈蚀时间t的关系为：

(4)

其中，t为锈蚀时间，s；Icor为腐蚀电流,A；M为铁元素摩尔质量，取56 g/mol；F为法拉利常数，取9.65×104C/mol；z为铁离子化学价位，取均值2.5。

单位长度钢筋的表面电流即为腐蚀电流密度icor，取计算长度10 mm，钢筋直径d的单位为mm，则腐蚀电流密度icor(μA/cm2)与腐蚀电流Icor(A)关系为：

(5)

依据钢筋密度ps=7.85 g/cm3，据文献[1]取icor≈100 μA/cm2，可求得ML：

(6)

(7)

其中，ρcr为钢筋开裂时锈蚀率。

5)张伟平开裂模型[7]。

δcr=kcrs(0.008c/d+0.000 55fcuk-0.002)

(8)

其中，kcrs为钢筋位置影响系数，在角区取1，非角区取1.04；据其统计，计算结果与试验之比的均值1.03，标准差0.153 6。

综合分析上述计算模型可知，前两种计算模型类似，后三种计算模型类似。

按照结构可靠度标准，钢筋锈胀开裂的功能函数为：

Z(t)=δcr-δ(t)

(9)

或:

Z(t)=ρcr-ρ(t)

(10)

功能函数在t时间内的失效概率为:

Pf=P{Z(t)≤0}

(11)

结构的可靠指标：

β(t)=μZ(t)/σZ(t)

(12)

结构的失效概率：

Pf=Φ[-β(t)]

(13)

可以看出功能函数中δcr,δ(t),ρcr,ρ(t)均具有随机性。

2 钢筋锈蚀深度的计算分析

由于张伟平开裂模型给出的是混凝土保护层开裂时候的钢筋的锈蚀深度，牛荻涛公式给出的是混凝土保护层开裂前的锈蚀深度值，因此，依据两个模型可以分别估算开裂时和开裂前的锈蚀深度。

另外，张伟平开裂模型中，根据实际的统计数据，给出了公式δcr的计算结果与试验之比的均值和标准差为：μ=1.03，σ=0.153 6，可以建立计算结果与试验数据之间的关系。同样，牛荻涛公式给出了预测模型的不定性随机变量Kcr的均值和标准差为：μ=0.794，σ=0.652，可以建立试验数据和考虑随机变量之后的实际数据的关系。综合考虑两个模型，即可建立混凝土保护层开裂时和开裂前的锈蚀深度实际数据差值的概率分布。

以耐久性年限20年，保护层厚度25 mm，钢筋直径16 mm的混凝土梁构件为例，计算参数：非角区kcr=1，c=25，d=16，fcuk=20 MPa代入张伟平公式得μδcr=0.023 031，σδcr=0.003 434。

计算参数：非角区kcrs=1.04，T=20，RH=0.5，室内干燥环境kce=1.0代入牛荻涛公式得μδ(t)=0.000 576 1(t-ti)，σδ(t)=0.000 473 0(t-ti)。

假设(t-ti)=20年，可求得μδ(t)=0.011 522，σδ(t)=0.009 46。

依据上述分析，钢筋锈蚀深度的功能函数为：Z(t)=δcr-δei(t)，求得使用20年梁构件的开裂时锈蚀深度的均值和标准差，与开裂前锈蚀深度的均值和标准差的概率分布关系，如图1所示，可知两曲线相重叠的部分即为失效概率，包括开裂时锈蚀深度≤开裂前锈蚀深度，和开裂前锈蚀深度≥开裂时锈蚀深度的概率之和。

针对梁构件，其可靠指标:

(14)

其中，t0=(t-ti)。

结构的失效概率：

Pf=Φ[-β(t)]

(15)

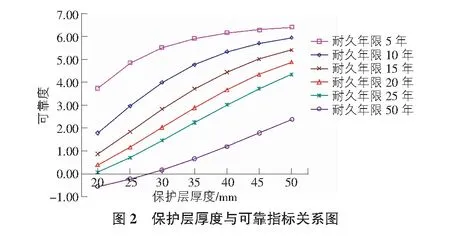
代入t0=20年到式(14)，得β(t)=1.14，对应正态分布图上的失效概率可以查正态分布表，失效概率为12.71%，同理按照相应的耐久年限(t0)和结构设计规范中的保护层厚度值可以计算相应的可靠指标，并查正态分布表得相应的失效概率，见表1。其中“/”代表失效可能性极小，失效概率小于0.01%，同时依据计算结果可以绘制保护层厚度与可靠指标关系图，如图2所示。

表1 不同保护层厚度时的失效概率表

3 结语

从图2可以看出，以保护层开裂作为寿命预测的标准，室内干燥环境，耐久年限(t0)为50年情况下，要满足可靠指标β≥0，需保证构件保护层大于28 mm。要满足可靠指标β≥1，需保证构件保护层大于38.2 mm。据此推测规范保护层可能是依据此并考虑可以带一定的裂缝工作，作为保护层厚度的确定标准，即在保护层开裂后，只要开裂宽度不达到一定值，都认为结构可靠。另外可以得出，保护层20 mm可以满足耐久年限25年及以下的可靠指标标准。保护层38.2 mm可以保证满足耐久年限50年的可靠指标大于1，即失效概率小于15%，保护层厚度的提高对耐久性的影响明显，提高保护层厚度可以有效改善构件的耐久性，提高构件的可靠度。本文分析了其中一种不定性系数的开裂深度的概率模型，可以考虑锈蚀率的概率模型，通过试验、验收规范或实际抽样样本，选定更精确的不确定系数，然后依据误差传递公式分别计算整个功能函数中各个抗力和作用的均值与标准差，再利用正态分布分析总体的可靠性。