发动机凸轮轴扭振和滚振特性研究

彭海雄,辛花,陈正虎,王小慧,熊毕伟,兰银在,阎玮,王晓滕

(1.中国北方发动机研究所(天津)，天津 300400；2.驻石家庄地区第三军事代表室，河北 石家庄 050000)

凸轮轴系作为整机或者曲轴主系统的一个重要分支，在配气机构运行过程中主要承受气门弹簧反作用力、气门动态冲击力及从动件等部件的摩擦及阻力矩等，凸轮轴的旋转速度从每分钟几百转至数千转，凸轮轴承受着较为复杂的弯扭载荷，特别是对于多缸发动机，其细长的凸轮轴更易与轴承座发生径向振动或自身的扭转振动问题，会导致疲劳破坏等情况发生。随着新型发动机研制水平的不断发展，发动机的功率和扭矩性能逐步提高，配气机构零部件的负荷也不断增加，造成凸轮轴所受负载激励变得越来越大，配气机构或正时传动系统的正常工作环境越来越恶劣。

目前，国内外文献主要集中在凸轮轴运动学、动力学模型构建及材料选取、金相显微分析方面。Saka等[1]对凸轮轴的扭振进行了研究，指出扭振是由挺柱与凸轮轴之间不断变化的接触力造成的，而扭振又会影响挺柱的运动及两者之间的接触力情况。Brian等[2]对某皮带轮驱动的凸轮轴扭振问题进行了研究，结果表明凸轮轴的扭振与气门动态响应之间并没有非常明显的关系。Bruce等[3]对凸轮轴扭振产生的原因进行了简述，提到凸轮轴扭振会带来凸轮轴驱动带或链系的疲劳、张紧器疲劳、产生噪声及自身疲劳断裂等问题。Li等[4]建立凸轮轴弹性扭振模型对柴油机喷油泵凸轮轴瞬态转速和油泵压力之间的关系进行了研究，结果表明凸轮轴转速波动与喷射正时和持续时间有着非常紧密的联系。孙鋆强等[5]研究了由于从动件对凸轮轴的作用使凸轮轴产生的扭转变形及其对振动的影响，绘制了不同运动规律对凸轮轴扭振影响的曲线。Teodorescu等[6]研究了凸轮轴扭振对配气机构动态特性的影响，获得了不同配气参数下的凸轮轴扭振曲线。陶景光[7]和邹德志[8]对凸轮轴的断口进行金相学分析，探究了凸轮轴的扭转弯曲疲劳性能。

滚振是扭振的一种特殊现象，WKer[9]认为柴油机装置“纯”滚时如同一个刚体装置，所有质量均作振幅相同的同相位振动，任何频率干扰下的扭转均可分为扭转与纯滚两部分，纯滚轴段不产生应力。李渤仲等[10]则将单结点出现之前轴系扭振定义为滚振。陈之炎[11]认为，滚振就是低频区的扭转振动，在单结结点出现之前的频率区称为滚振区，它不是纯滚，但这时的振动统称为滚振。吴炎庭[12]认为，对于强迫振动，激励力矩输入系统的能量是激起系统强迫振动的源头，激励力矩矢量和是由简谐激励力矩及相对振幅矢量和这两个因素决定的，低次主简谐具有较大的激励力矩矢量值，低次主简谐最容易激起滚振波，这就是低速区经常出现最低次主简谐次滚振的根据。

综上所述，滚振理论上分为纯滚与扭振两部分，在单结结点出现时的频率可视为分界点，在它以下的频率区内，纯滚是主要分量，并且频率越低，它所占的比例越大。在它以上的频率区内，扭振是主要分量，频率越高，纯滚越小。前者称为滚振区，两个连续减振点频率之间的区域称为相应各结的扭振区，即将系统在整个频率范围的响应曲线分为滚振区、单结扭振区、双结扭振区等。

吴斌等[13]建立了4缸汽油机怠速闭环控制系统及曲轴滚振测试系统，并发现在650 r/min，800 r/min，1 000 r/min 3种怠速工况下，发动机0.5谐次滚振的平均幅值最大且存在着较大的循环波动。胡宇宁[14]通过曲轴系统多体动力学仿真分析，发现600～1 800 r/min转速区间3谐次频率下主要表现为滚振特征。Huang等[15]根据瞬时功能等效法，建立多缸曲轴总成非线性动力学模型，发现随着往复惯量转矩的增大，滚动振动在低谐次范围内减小，而扭转振动有增大的趋势。整体来看，发动机扭振和滚振特性研究主要集中在曲轴，对于凸轮轴的研究一般都是当凸轮轴(特别是喷油泵凸轮轴)出现疲劳断裂的时候进行常规的金相检测等研究，对于大功率发动机凸轮轴轴颈受较大交变载荷作用时是否存在强烈激振尚不明确。

本研究采用集中质量法，基于某V12柴油机建立发动机多体动力学模型，获取进排气左右凸轮轴强迫扭振边界条件，分析凸轮轴强迫振动谐次。推导滚振物理模型并提出了通过多次近似拟合低转速下的振幅结果以消除滚振误差的方法。调研简谐系数适应工况、内燃机机型，得到试验柴油机滚振计算公式并估算滚振幅值，避开了较繁琐的凸轮轴系建模阶段，与所建立的发动机多体动力学模型滚振幅值对比，验证凸轮轴滚振振幅估算曲线的准确性。

1 凸轮轴系多体动力学建模

试验采用V12柴油机，借助AVL Designer和AVL Timing Driver软件建立试验发动机动力学模型，基于多体动力学方法获取凸轮轴强迫扭振的边界激励条件，进行凸轮轴强迫扭振计算。发动机轴系扭振计算流程见图1。

图1 发动机轴系扭振计算流程

1.1 试验柴油机基本参数

试验V12柴油机基本参数见表1。单阀系建模包括旋转激励单元、凸轮轴段及支撑轴承单元、轴段与气阀连接单元、凸轮单元、油膜单元、机械挺柱单元、气门杆单元、气门单元和内外气门弹簧单元。其中，进/排气单阀系模型的模块是一致的，排气单阀系的气门单元需加载燃烧压力。前端齿轮的动力输出附件主要包括机油泵、发电机、水泵、喷油泵和4根凸轮轴，前端齿轮传动系统在建模过程中需要齿轮的质量系参数，包括齿轮单元质量、转动惯量及弯曲惯量。齿轮之间的啮合参数包括重心坐标、齿数、外径、齿宽、螺旋角和压力角等。

表1 试验柴油机基本参数

1.2 柴油机扭振模型的搭建

定义坐标系，以曲轴主轴颈轴心线为X轴，Z轴垂直于曲轴中心线并且与第一拐平行，Y轴垂直于XZ平面(见图2)。

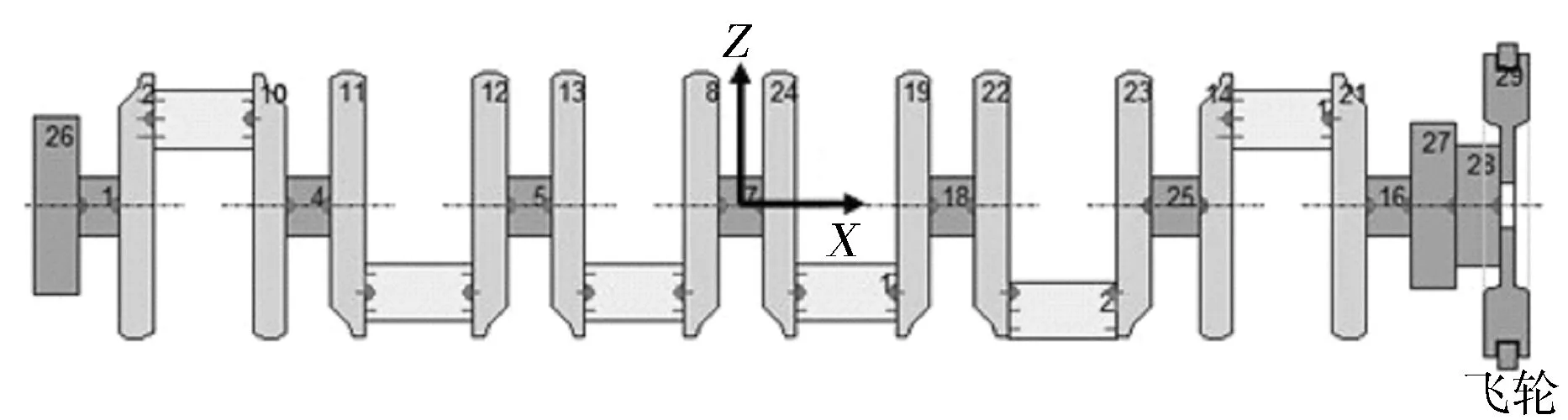
图2 曲轴主视图

扭振轴系的部件主要包括凸轮轴、正时齿轮、曲轴、活塞连杆组、飞轮系、皮带轮、减振器、正时齿轮、挡油环等。通过集中质量法，搭建试验柴油机扭振模型(见图3)。当量化之后共有159个节点：节点1为曲轴前端轴段；节点1～23为曲轴前端至飞轮端的当量惯量；节点24～42为前端正时齿轮的当量惯量；节点43～159为凸轮轴的当量惯量。

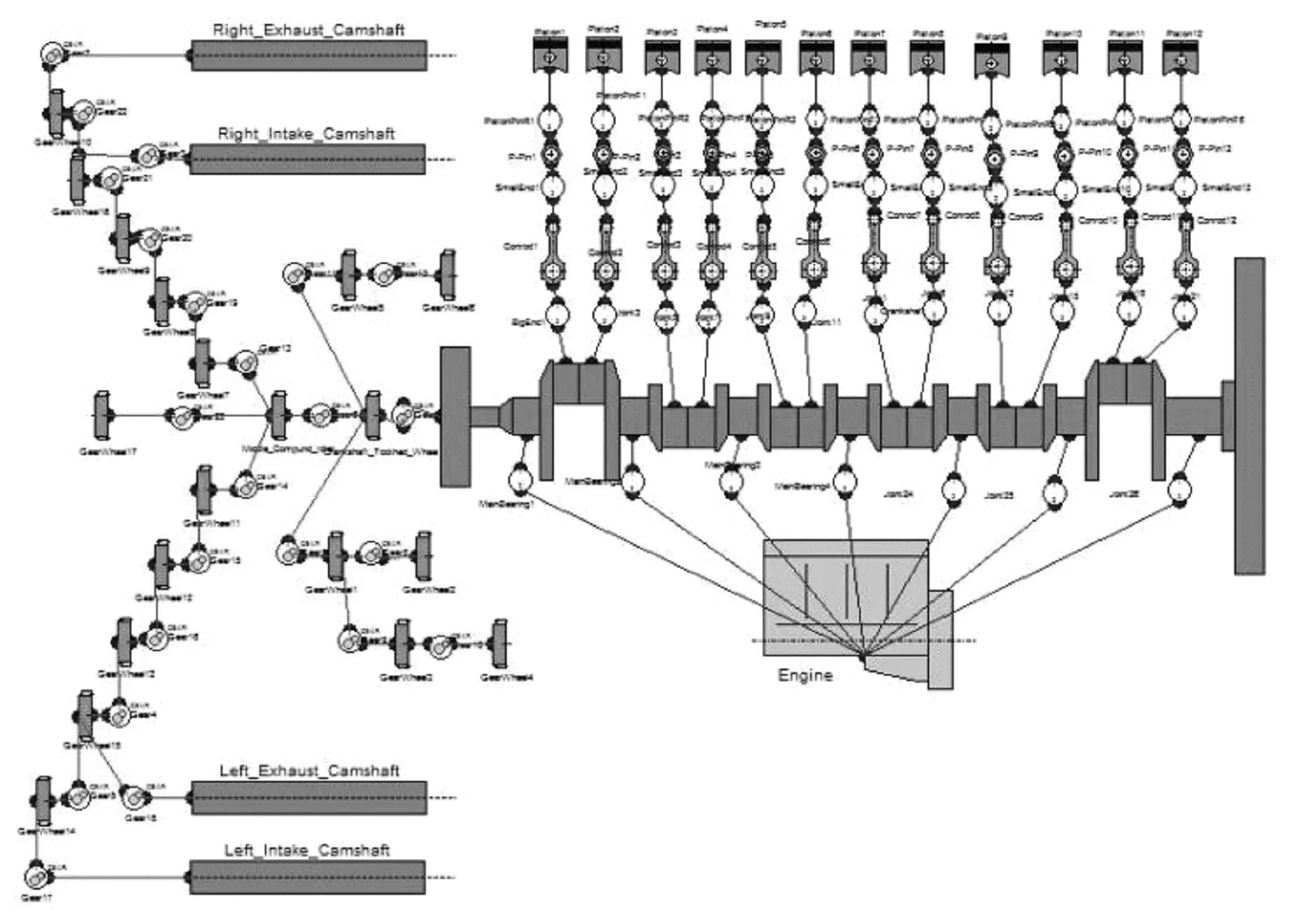
图3 试验柴油机系统模型

根据建立的柴油机多体动力学模型，获取凸轮轴强迫扭振计算中800～2 500 r/min转速范围内的负载扭矩激励，计算凸轮轴系强迫扭振，获取前20谐次(即0.5谐次，1谐次，……10谐次)下扭振特性。

2 扭振系统计算结果及分析

基于仿真模型获取试验V12柴油机4根凸轮轴强迫振动特性，以左向进气凸轮轴为例，分析13个转速点下凸轮轴强迫扭振结果(见图4)。

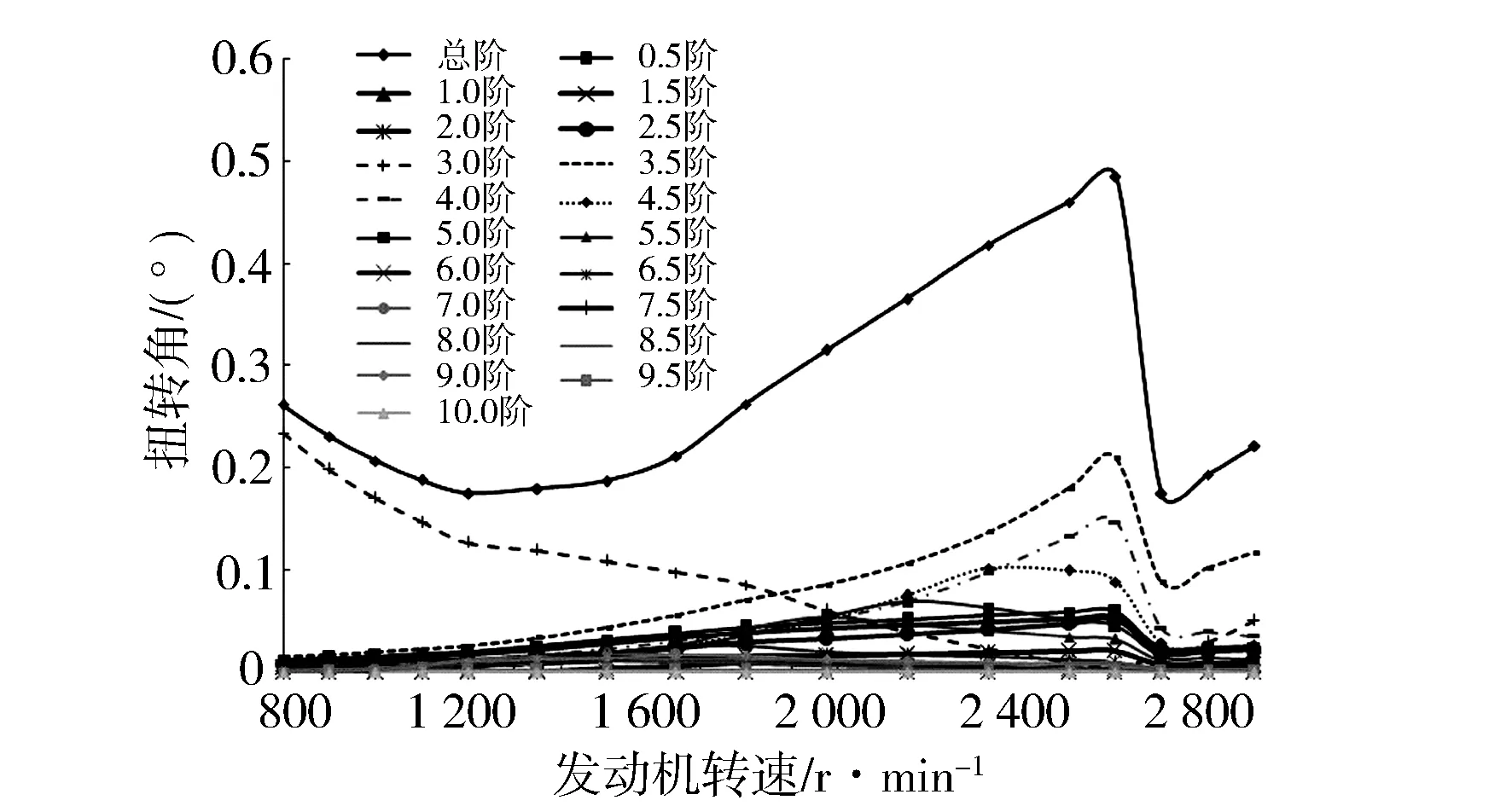
图4 发动机左向进气凸轮轴强迫扭振振幅

图4示出左向进气凸轮轴自由端在各个转速下的强迫扭振振幅最大值和分解后的谐次曲线振幅贡献结果。由图4可知，总阶在800～2 500 r/min范围内是呈先递减再递增的趋势，2 500 r/min时达到扭振最大幅值0.46°。2 500 r/min时的峰值主要由第3.5，4.0和4.5谐次峰值贡献获取。为便于直观分析各凸轮轴谐次信息，提取主要谐次振幅曲线，结果见图5。

由图5a可知，左向进气凸轮轴第3.5及4.0谐次在逐渐增大，其峰值在2 500 r/min之后，不在转速范围之内。在2 325 r/min，2 150 r/min，1 975 r/min，1 650 r/min时，第4.5谐次、第5.0谐次、第5.5谐次及第6.5谐次出现了明显的峰值，其中第4.5谐次扭振峰值达到了0.10°。以上结果表明，第3谐次振幅随转速增大而呈递减趋势，是引起滚振的主要谐次。由图5b、图5c、图5d可知，左向排气凸轮轴和右向进排气凸轮轴存在同样的谐次变化规律。

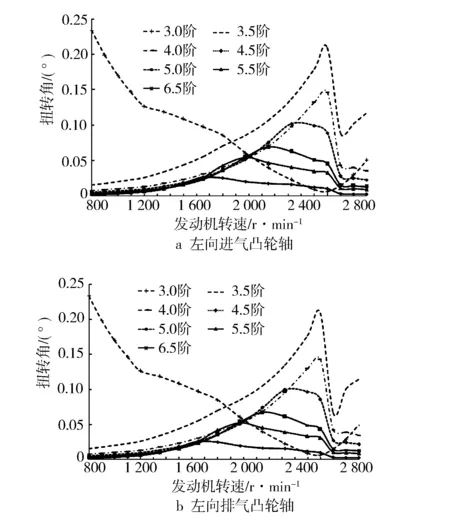
图5 发动机凸轮轴强迫扭振主要谐次振幅曲线

凸轮轴总体强迫扭振振幅对比结果见图6。由图6可知，凸轮轴扭振振幅在全转速范围内都是呈先递减再递增的趋势，左右向的凸轮轴扭振振幅均在1 200 r/min处达到振幅最低峰值并开始递增，扭振的最高峰值均出现在2 500 r/min转速工况。且右向侧的排气凸轮轴振幅略大于右向侧的进气凸轮轴，左向侧的进气凸轮轴振幅略大于左向侧的排气凸轮轴。左向的凸轮轴扭振振幅在中高转速时要明显低于右向的凸轮轴振幅，而同向的凸轮轴振幅曲线则非常接近，呈现非常显著的侧向性偏振现象。而这种偏振现象是双侧对称布置的V型发动机的一种固有特性，受主副系统上同时作用的同谐次干扰所影响，是发动机中两个相同的分支(左右向的凸轮轴系)为主系统延伸出来的一部分的平行阵型和作为系统本身的对称阵型叠加起来而综合作用的结果。由凸轮轴扭振分析可知，3谐次的激励力矩是构成滚振的主要成分。

图6 发动机凸轮轴强迫扭振振幅对比

3 凸轮轴滚振分析

3.1 凸轮轴滚振理论模型建立

滚振，又称“脉动”，也有人称之为“零结点振动”。其运动规律是轴系任一截面都以相同的振幅作同步的来回转动。它投射在平面上也是半径的摆动，但摆动的幅度在各截面上是一样的，且摆动方向一致，在阵型图上是一条水平线，显然，滚振有交变的角位移，但没有附加应力。

柴油机轴系作滚振时，轴系中各质量的振幅幅值及其相位均相等，系统的滚振阵型为

a1=a2=…=ai=AR=1。

(1)

式中：ai为第i个质量相对振幅；AR为滚振振幅。

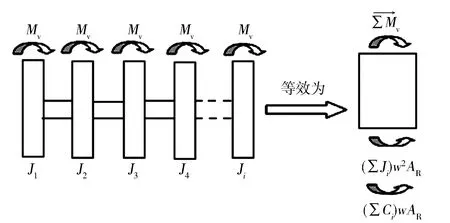
图7 系统中的滚振

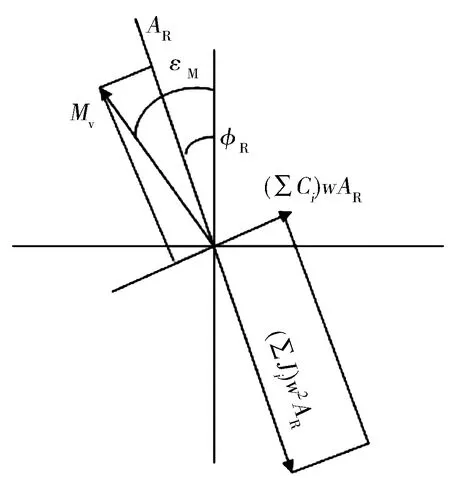
图8 滚振运动矢量平衡关系

(2)

[(∑Ci)·w·AR]2=

(3)

于是得到滚振振幅和相位：

(4)

εR=εM-arctan(∑Ci/w∑Ji)。

(5)

式中：CRv称为“简谐系数”；εM为激励力转动相位；v为简谐次数，由柴油机试验或经验曲线公式求得。

3.2 凸轮轴滚振振幅计算

3.2.1 滚振振幅确定

在低转速时的主要成分是滚振，先测量出试验发动机最低稳定转速n1时的振幅值AR1，忽略阻尼影响，视为该转速下的滚振振幅，公式为

(6)

由于式(6)中未考虑阻尼，为了补偿由于阻尼而产生的相位影响，用系数ζ加以修正，K为滚振系数。

(7)

假设最低稳定转速n1时的振幅值取决于滚振值AR1，以此为基础估算任意转速ni时的滚振振幅值ARi，在尽可能较小的稳定转速下，多取几组低转速下的振幅结果近似拟合以消除误差。

(8)

3.2.2 简谐系数求取

柴油机的简谐系数CRv亦称为简谐激励力矩系数，是扭振计算中的重要数据，为了对柴油机轴系在规定转速范围内任一工况进行强迫振动计算，须获取柴油机简谐系数。以往对轴系扭振分析时采用的是1972年英国劳氏船级社推荐的简谐系数通用计算公式，但是存在较大的误差。最小二乘法对拟合柴油机的简谐系数具有较好的效果[16-17]，因此，简谐系数的求取采用该方法进行拟合估算。

从简谐系数的研究得知，影响简谐系数的因素有平均指示压力、增压压力、压缩比、最高燃烧压力、压缩指数和膨胀指数等，平均指示压力是最主要的因素，因此，目前在扭振计算中一般都把简谐系数看成是平均指示压力的函数，用多项式表示：

(9)

式中：pi为柴油机平均指示压力；a为待确定系数。

从扭振计算的实际情况看，当幂指数m的取值范围为1～3时可满足扭振计算的精度要求，国外一些典型的简谐系数计算公式中关于m的取值情况见表2。

表2 简谐系数最高幂指数m取值

英国劳氏船级社按线性曲线给出的计算公式较适用于低速机，而按三次曲线给出计算公式则较符合中速机或中高速机的情况。因此，本研究中试验柴油机的m取为3。根据试验柴油机不同负荷工况示功图获取各工况下各个谐次简谐系数拟合曲线。由凸轮轴扭振分析可知，3谐次的激励力矩是构成滚振的主要成分，简谐系数的计算公式只考虑第3谐次的激励情况，可描述为

(10)

4 凸轮轴滚振分析

试验发动机进排气左右凸轮轴第3谐次激励力矩振幅曲线见图9。对比图9可得，左进排气凸轮轴滚振振幅相同，右进排气凸轮轴滚振振幅相同；左进排气凸轮轴滚振振幅整体大于右进排气凸轮轴；在800～2 500 r/min转速范围内，1 200 r/min后滚振振幅下降减慢。

图9 凸轮轴第3谐次激励力矩振幅曲线

以左向排气凸轮轴为例，低转速800 r/min时，其扭振振幅为0.26°，并近似认为是纯滚振振幅，以此为基准参照式(9)估算其余转速下的滚振振幅，并与滚振波第3谐次简谐振幅值进行对比，对比结果见图10。

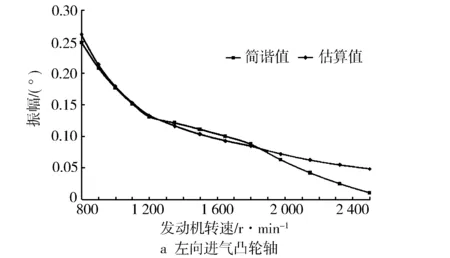
图10 发动机滚振估算值与第3谐次幅值对比

由图10a和图10b可知，左向进排气凸轮轴滚振在800～1 250 r/min范围估算值略大于简谐值，此区间估算值与简谐值基本吻合；在1 250～1 860 r/min范围简谐值略大于估算值；当转速大于1 860 r/min时，简谐值快速下降，而估算值下降缓慢。由图10c和图10d可知，右向进排气凸轮轴滚振在800～1 200 r/min范围估算值略大于简谐值，此区间估算值与简谐值基本吻合；在1 200～1 920 r/min范围简谐值略大于估算值；当转速大于1 920 r/min时简谐值快速下降，而估算值下降缓慢。

由图10可见，凸轮轴滚振估算与简谐曲线可分为三个阶段。当转速提升时，增压压力、压缩比、最高燃烧压力、压缩指数和膨胀指数等因素也会相应提升，上述指标同样影响柴油机简谐系数，导致较高转速下简谐系数估算值偏低。由式(9)可知，简谐系数与滚振幅值呈正比，简谐系数偏低使凸轮轴滚振曲线第二阶段估算滚振振幅偏低。凸轮轴的滚振只发生在低转速工况，随转速增加，滚振幅值减小。当转速范围超过某一临界值时，估算获得的滚振振幅实际为滚振与扭振的复合结果，导致滚振估算曲线第三阶段偏高。综上所述，在800～1 900 r/min范围内试验柴油机进排气左右凸轮轴滚振估算值与简谐值偏差小于0.02°，试验柴油机在此范围区间产生滚振，滚振估算结果与仿真结果具有较高的一致性。

5 结论

a)凸轮轴强迫扭振振幅的主要贡献谐次为第4.5，5.0，5.5及6.5谐次，在2 500 r/min转速区域时凸轮轴扭振振幅峰值均达到最大值，总体比较右向凸轮轴强迫扭振振幅要比左向凸轮轴强迫扭振振幅大，存在一定的偏振；第3谐次随转速增大其幅值呈现递减趋势，是引起凸轮轴滚振的主要低频谐次因素；

b)分析计算发动机进排气左右凸轮轴滚振幅值特性，进行了800～2 500 r/min转速工况滚振幅值预测，结果表明，预测结果与柴油机扭振模型第3谐次简谐值在中低转速时幅值比较接近，在800～1 900 r/min范围内凸轮轴滚振估算值与简谐值偏差小于0.02°，满足较低转速滚振计算要求。