L节匹配网络的应用条件

李晓春， 张 晗

(上海交通大学 电子信息与电气工程学院， 上海 200240)

0 引言

在微波射频电路中，匹配网络对于系统功能的正确实现至关重要。其中，仅由两个电抗性元件构成的L节匹配网络是一类简单的匹配网络[1]。尽管在实际应用中，这种匹配网络有着频率、带宽等诸多方面的限制，但在教学过程中，这种形式简单的匹配网络能够帮助学生更好地学习和理解单支节匹配、双支节匹配等其他类型的匹配网络[1～3]。

文献[1]作为微波理论技术方面的经典教材，对两种形式的L节匹配网络进行了理论推导，并结合了Smith圆图加以分析。但是，在这两种形式电路的使用条件上，文献[1]的阐述并不完善。

本文从理论上严格推导了使用两种形式的L节匹配网络时各自所需的充要条件，并结合Smith圆图加以验证。为了便于教学应用，本文给出了自制的L节匹配网络程序，并结合程序进行了实例分析。

1 L节匹配网络使用条件的理论推导

L节匹配网络的两种拓扑结构如图1所示，表示将负载阻抗ZL匹配到目标阻抗Z0。其中，X为电抗值，B电纳值。值得注意的是，X和B的取值可以为正，也可以为负。如果用集总元件实现L型匹配网络，当X为正或B为负时，均对应电感；当X为负或B为正时，均对应电容。

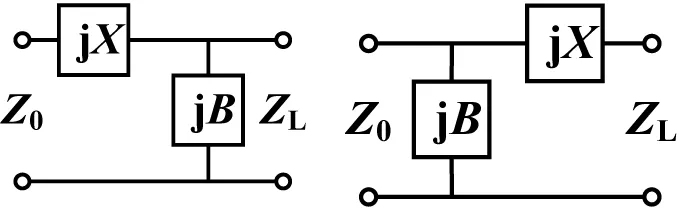
(a) 先串后并型 (b) 先并后串型图1 L节匹配网络

(1)

其中，RL和XL分别为ZL的实部(电阻)和虚部(电抗)。在阻抗匹配中，常见的一种情况是将负载阻抗匹配到传输线的特征阻抗，并将特征阻抗近似为正实数进行设计。此处采用该假设，认为Z0为正实数，则可将式(1)的实部和虚部分开，整理得到关于X和B的两个等式：

RLBX-Z0XLB+Z0-RL=0

(2)

XLBX+Z0RLB-X-XL=0

(3)

从式(2)和式(3)中消去X，可给出关于B的二次方程

Z0(RL2+XL2)B2-2Z0XLB+Z0-RL=0

(4)

式(4)有实数解的充要条件为

Z0RL(RL2+XL2-Z0RL)≥0

1)数据中心的硬件技术架构可以采用操作数据存储(ODS)+分布式存储集群(Hadoop)+数据集市(DM)的混合架构，来满足数据中心对海量异构数据的处理需求。

(5)

先并后串型L节匹配网络可使用的充要条件，即为式(5)给出的不等式。根据上述假设，Z0为正实数；同时，负载ZL的电阻RL通常也为正，因此式(5)可简化为

RL2+XL2-Z0RL≥0

(6)

文献[1]给出的使用先并后串型L节匹配网络的条件为RL≥ZL，在此条件下式(6)恒成立。然而，该条件并非充要条件。事实上，可以从式(6)得到更简单的等价形式。将式(6)变形可得

(7)

注意到不等式的左边为负载的电导GL，不等式的右边为目标阻抗的导纳Y0，因此式(7)又可写为

GL≤Y0

(8)

式(8)即为先串后并型L节匹配网络可以使用的充要条件，即负载电导不大于目标导纳。

图1(b)所示先串后并型L节匹配网络可以使用的充要条件通过类似过程推得为

RL≤Z0

(9)

即负载电阻不大于目标阻抗。此条件与文献[1]结论相符。

2 L节匹配电路的Smith圆图验证

图2展示了通过Smith阻抗导纳圆图进行L节阻抗匹配的过程。其中，等电阻圆(包括单位电阻圆)在图的右上侧标示，等电导圆(包括单位电导圆)在图的左上侧标示，zL为归一化负载阻抗

zL=ZL/Z0

(10)

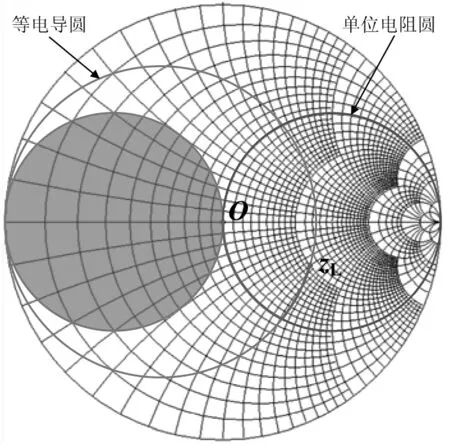
(a) 先并后串型

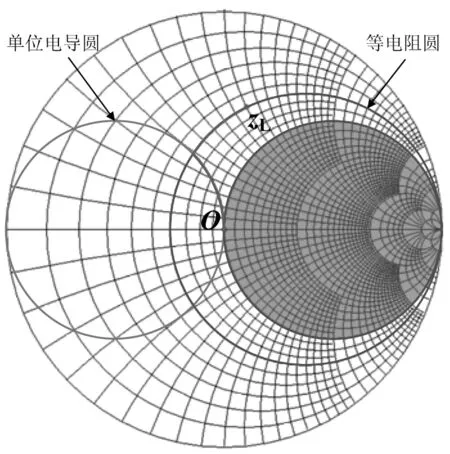
(b) 先串后并型图2 Smith圆图示意L节匹配过程

对于先并后串型L节匹配网络，负载首先与电纳元件并联，此时输入电导是不变的，因此归一化负载阻抗点zL沿等电导圆旋转，移动到等电导圆与单位电阻圆的交点。其中，单位电阻圆上的点所对应的归一化电阻值均为1。然后，负载又与电抗元件串联，此时输入电阻不变，因此归一化负载点再从上述交点处沿单位电阻圆移动到原点O，实现与目标阻抗的匹配。可以看出，为了使用先串后并型L节匹配网络进行阻抗匹配，需要满足的条件是归一化负载阻抗点zL所在的等电导圆与单位电阻圆有交点(包括相切)。在Smith圆图中，这一条件等价于归一化负载阻抗点zL不在单位电导圆内部，即图2(a)中阴影区域，意味着需要满足条件

gL≤1

(11)

其中gL为归一化电导

gL=GL/Y0

(12)

该条件与式(8)一致，验证了前面公式推导的正确性。

类似的，我们可以得到，使用先并后串型L节匹配网络时，需要满足的条件是，归一化负载阻抗点zL不在单位电阻圆内部，即图2(b)中阴影区域。该条件等价于

rL≤1

(13)

其中rL为归一化电阻

rL=RL/Z0

(14)

与式(9)给出的条件一致。

3 自制程序实例

自制L节匹配网络程序的图形化界面如图3所示。界面左侧包括目标阻抗、负载和L节匹配电路形式的输入窗口，以及结果的显示窗口；界面右侧为Smith圆图。当输入完成时，单击计算按钮，结果显示窗口将给出L节匹配电路中元件的数值，同时Smith圆图中将显示匹配过程。

图3 L节匹配网络程序界面

图3给出的算例中，目标阻抗Z0=50 Ω，负载阻抗ZL=40+j40 Ω。按照文献[1]中给出的L节匹配电路选择条件，此时负载电阻RL=40 Ω，满足RL

该程序可以在教学过程中使用，帮助学生理解L节匹配电路的原理。

4 结语

本文从公式推导和Smith圆图两个角度，给出了两种形式的L节匹配电路的使用条件，完善了传统研究方法中的不足。在此基础上，本文采用自制程序，通过一个具体例子进一步验证了文中提出的充要条件，加深了对L节匹配电路的理解。