“数字信号处理”中分段滤波的教学探讨
王倩雯, 毛卫宁
(东南大学 信息科学与工程学院,江苏 南京 210096)
0 引言
随着电子、通信技术和计算机网络的快速发展,数字信号处理技术得到了长足进步,并广泛应用于雷达、声纳、数字通信、图像处理、模式识别、遥感遥测、生物医学等领域。与此同时,在理工科高等院校的教学体系中,“数字信号处理”课程的地位日显重要,不再局限于通信与电子工程专业,在自动控制、机械电子、生物医学等学科得到普及,成为这些专业的必修或选修课程。
滤波是数字信号处理最基本的环节。线性卷积是计算线性时不变滤波器响应的主要方法之一,许多重要应用都建立在这一理论基础上。对于有限长单位脉冲响应滤波器,可以用圆周卷积代替线性卷积,计算滤波器的输出,但当滤波器输入信号的长度与单位脉冲响应长度相差较大时,需要采用分段滤波的方法,将输入信号分为许多段,每段的长度与单位脉冲响应长度接近,每段滤波用圆周卷积计算,具体有两种实现方法:重叠相加法和重叠保留法。
重叠相加法和重叠保留法是“数字信号处理”课程的重要知识点和难点之一,在实际工程中应用广泛[1~4],其实质是要保证各段滤波输出的连续性。现有教材和课堂教学中均从循环卷积与线性卷积关系出发讨论重叠相加法和重叠保留法,有一定的局限性,本文通过分析滤波器的稳态响应和瞬态响应,阐述重叠相加法和重叠保留法如何实现各段滤波输出的连续性,并讨论了重叠相加法和重叠保留法各段线性卷积与圆周卷积的关系,以及各段滤波输入/输出数据的关系。
1 重叠相加法
对于线性时不变系统,若系统的单位脉冲响应为h(n),长度为M,重叠相加法将长序列x(n)分解为若干段,每段长度为N,用xi(n)表示x(n)序列的第i段:

(1)
则输入序列可表示为:
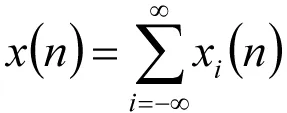
(2)
滤波输出可表示为:
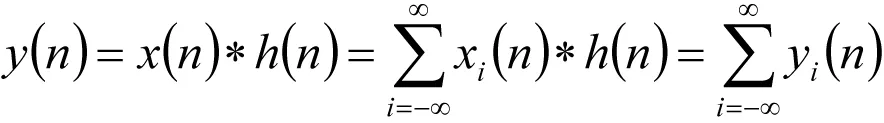
(3)
其中yi(n)=xi(n)*h(n)为第i段的线性卷积,其有N+M-1个非零样本,而每段输入数据长度为N,故相邻两段的卷积结果有(M-1)点重叠,根据式(3)重叠部分相加得到输出序列 。
对于重叠相加法,一般教材[5~7]都根据式(3)讨论算法原理和计算步骤,并未从滤波的物理概念上阐述如何保证各段滤波输出的连续性,学生知其然,不知其所以然,影响该知识点的正确理解掌握和运用。
分析第i-1段和第i段滤波器的输出表明,第i-1段最后M-1点滤波器的输出为
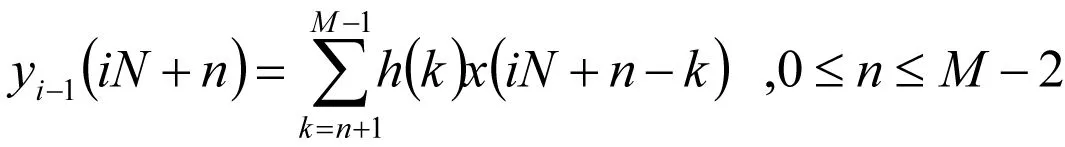
(4)
由于每段输入数据长度为N,每段最后M-1点,滤波器的输出逐渐减小,如图1;而第i段前M-1点滤波器的输出为
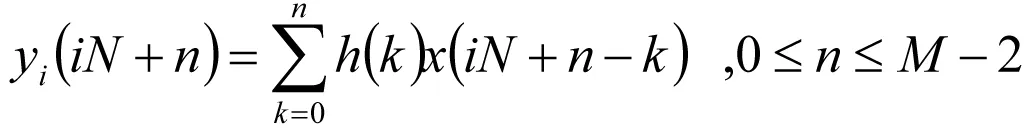
(5)
滤波器的输出随n逐渐增大,直到n=M-1,如图1所示。式(4)和(5)为滤波器的瞬态响应,两者相加得
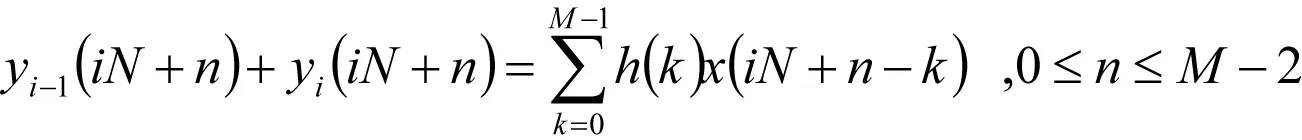
(6)
式(6)是滤波器的稳态响应,式(6)解释了为何相邻两段卷积结果相加可保证各段滤波输出的连续性。算法实现时,每一段滤波输出可用圆周卷积计算,取圆周卷积的长度L≥N+M-1,故对于重叠相加法,每一段线性卷积等于圆周卷积,而各段滤波的输入序列顺序选取。

图1 重叠相加法各段输入输出数据关系
2 重叠保留法
重叠保留法将长序列x(n)分段,相邻两段输入序列重叠(M-1)点,每段输入序列xi(n)长为N点;对xi(n)与h(n)计算N点的圆周卷积,并去掉有混叠的前(M-1)点,之后顺次相连得到总的滤波输出。
由于圆周卷积的长度等于各段输入序列的长度,因而圆周卷积前(M-1)点有混叠,不等于线性卷积,一般教材[5~7]从圆周卷积与线性卷积的这种关系出发,讨论重叠保留法原理和实现方法。事实上,对于重叠保留法,每段线性卷积的长度,即滤波器的输出为N+M-1点,每段输出去掉前(M-1)点是由滤波器的输出特性决定的,而非圆周卷积的混叠点数。圆周卷积不等于线性卷积产生混叠的点数取决于圆周卷积的长度。分析各段滤波器输出的稳态响应和瞬态响应,可以很好地解释这一问题。
第i段滤波器的输出为

(7)
共N+M-1点。当M-1≤n≤N-1时, 滤波器输出为稳态响应,如式(7)所示;当0≤n≤M-1时,

(8)
当N≤n≤N+M-2时,
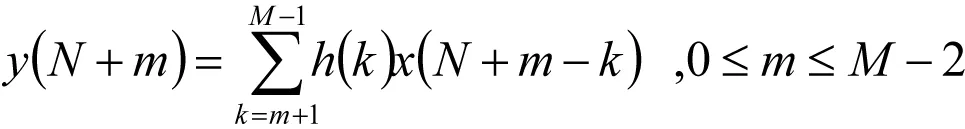
(9)
式(8)、(9)为滤波器的瞬态响应,在每段N+M-1点滤波输出中,前后各有M-1点瞬态响应,如图2所示。为保证各段滤波输出连续,每段滤波输出的前、后M-1点的瞬态响应都要舍弃,因而各段输入数据要重叠M-1点,各段输出取M-1~N-1点。算法实现时,用圆周卷积计算各段滤波输出时,圆周卷积的长度L不一定等于各段输入序列的长度,当L≥N+M-1时各段圆周卷积等于线性卷积,没有混叠,但为保证各段滤波输出连续,各段输出依然要舍弃前后各(M-1)点,取M-1~N-1点,而各段输入要重叠M-1点。
从滤波器稳态响应和瞬态响应出发解释重叠保留法,有助于学生正确理解该知识点,澄清概念,更好地运用于实际。结合上述分析,表1给出了重叠相加法和重叠保留法各段线性卷积与圆周卷积的关系,以及各段滤波输入/输出数据的关系。

表1 重叠相加法和重叠保留法各段滤波输入/输出数据间关系
3 结语
现有教材和课堂教学中从循环卷积与线性卷积关系出发,讨论重叠相加法和重叠保留法,有一定的局限性。本文从滤波器的瞬态响应和稳态响应出发,阐述重叠相加法和重叠保留法,并讨论了重叠相加法和重叠保留法各段线性卷积与圆周卷积的关系,以及各段滤波输入/输出数据的关系。这种从滤波器的物理机理出发,阐述分段滤波本质的方法,有助于提升学生从物理概念出发解决实际问题的能力,取得了较好的教学效果。

图2 重叠保留法各段输入输出数据关系

