线驱动柔性臂捕获装置的多体动力学特性分析
蒋万里 唐 斌 张 平
(大连理工大学 能源与动力学院,大连 116024)
清理太空碎片对航空航天事业的发展乃至人类未来的太空探索具有重要意义。由于太空环境的限制,太空碎片的清理工作只能交由机器人来做。与传统刚体机器人相比,柔性机械臂具有冗余度高、灵活性好以及适应性强等优点[1]。但是,柔性机械臂在执行捕获任务时产生的碰撞力,不仅会使柔性机械臂的收拢轨迹产生偏差,还会使柔性机械臂出现大幅度振动,甚至使目标物体逃逸导致任务失败。因此,针对太空碎片清理分析柔性机械抓取臂的多体动力学特性十分重要。
目前,国内外研究的重点是线驱动机械臂的实物结构创新,研究过程较为耗材费时。针对一些无重力等特殊环境,较难实现实物模拟。基于线驱动柔性机械臂的特点,提出了一种多柔体动力学模型的建模方法,可以较好地进行软材料机械臂的动力学模拟。最后,通过对比仿真结果和实际运动轨迹,验证了该方法的正确性,完成了线驱动柔性机械臂捕获装置的建模及动力学仿真。
1 多柔体动力学模型
1.1 数学建模
从拉格朗日方程导出柔性体的动力学方程为:

式中:Ψ为约束方程;λ为对应于约束方程的拉氏乘子;ξ为广义坐标;Q为投影到ξ上的广义力;L为拉格朗日项,定义为L=T-W,T和W分别表示动能和势能;Γ表示能量耗损函数。?
将求得的T、W和Γ带入式(1),可得:

式中:M为柔性体的质量矩阵;为质量矩阵对广义坐标的偏导数,是一个(N+6)×(N+6)×(N+6)维的张量;N为模态数[2]。
本文研究的线驱动柔性机械臂的多柔体模型,如图1所示。模型由柔性梁连接的6段柔性锯齿单元组成,柔性臂左端固定,右端施加相互垂直的两个分力。柔性臂尺寸为178 mm×25 mm×38 mm,杨氏模量为50 MPa,泊松比为0.48,密度为2 000 kg/m3,阻尼比为0.9。

图1 线驱动柔性臂
先建立每段柔性单元的有限元模型,再使用Craig-Bampton法求出每段单元的节点位移列向量μ与正交模态坐标ql的关系[3]:

式中:ϕi为第i个正交Craig-Bampton模态;qli为第i个模态坐标;N为所选模态的阶数。
因此,线驱动柔性机械臂的多柔性体动力学方程为[4]:

式中:Mf为总质量矩阵;Cf为总阻尼矩阵;Kf为总刚度矩阵;ff为不计碰撞力的总外力列向量;qf为广义位移列向量。
相邻两段柔性单元之间存在间隙,间隙间产生的接触碰撞力FN以非理想约束反力作用于系统,因此特定情形下需考虑带有间隙的多柔体系统的动力学方程。
2 模型验证
以多柔体动力学模型为基础,对图1柔性臂进行运动轨迹分析和模型验证,如图2所示。图2中的实线为柔性臂在5 N牵拉力作用下的运动轨迹,其中标记点1至标记点4的位置如图1所示。在仿真柔性臂右端施加3 N的水平驱动力和4 N的垂直驱动力,仿真运动轨迹如图2中虚线所示,模型整体变形如图3所示。
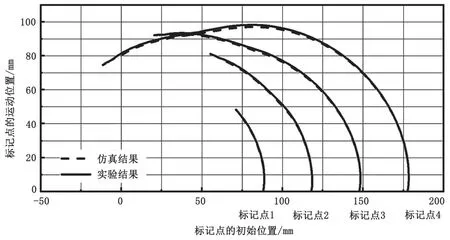
图2 运动轨迹对比

图3 柔性臂变形和仿真结果
通过比较可以看出,多柔体模型与线驱动柔性臂的弯曲轨迹和整体变形吻合度较高,可以较好地模拟线驱动柔性臂的弯曲变形。
3 多体动力学特性分析
3.1 驱动力和阻尼比对运动轨迹的影响
在多柔体模型的基础上,取阻尼比为0.9,分别对模型施加合力为1 N、3 N和5 N的驱动力,结果如图4所示。结果表明,在不同驱动力的作用下,柔性臂的运动轨迹有差异,驱动力越小,柔性臂包络的区域越大。
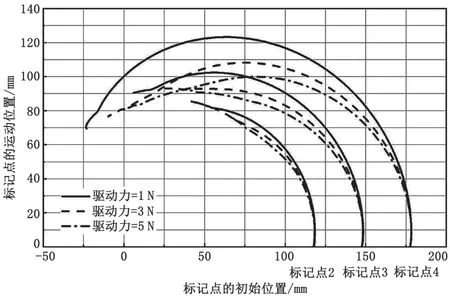
图4 不同驱动力下标记点的运动轨迹
在多柔体模型上施加合力为5 N的驱动力,分析阻尼比为0.9、1.5和2时的柔性臂运动轨迹结果如图5所示。结果表明,阻尼比与柔性臂包络区域的大小成正比。
3.2 捕获装置的建模及动力学仿真
为了模拟线驱动柔性臂的捕获过程,在多柔体柔性臂模型的基础上,建立了捕获装置整体模型。该捕获装置由4根柔性臂和固定装置组成。在无重力状态下,分析线驱动柔性捕获装置对球形目标物体的仿真抓取过程,如图6所示。从图6可以看出,球形目标物体先被柔性臂包拢,然后被柔性臂环抱着向固定装置的方向移动,最后被锁定在固定装置中,实现了捕获。

图5 不同阻尼比下标记点的运动轨迹

图6 捕获过程仿真
4 结语
针对线驱动柔性机械臂装置捕获目标物体过程中的碰撞问题,提出了一种多柔体动力学模型的建模方法,分析了线驱动柔性机械臂装置捕获过程中的多体动力学特性。
(1)建立的多柔体动力学模型能够较好地模拟线驱动柔性机械臂的运动轨迹和整体变形状态。
(2)驱动力和阻尼比对线驱动柔性机械臂装置的捕获轨迹有影响。捕获范围与驱动力负相关,与阻尼比正相关。
(3)基于线驱动柔性机械臂模型建立的捕获装置,在无重力环境下,能完成对目标物体的包拢和捕获。
鉴于柔性臂的材料和结构越来越复杂,提出的建模思路和方法具有一定的参考价值。

