狭窄空间内复杂产品的装配路径规划研究

熊 晶 段晓坤

（常州信息职业技术学院，常州 213164）

产品装配路径规划是产品装配工艺设计的重要内容之一。尤其是复杂产品，它的零部件数量多，结构复杂，内部空间紧凑。在狭窄空间内为待装配的零部件计算出一条从装配起点到装配终点的无碰撞路径，是虚拟装配设计的难点之一。

基于几何图的路径规划算法，如栅格法[1]，在路径搜索之前，先对整个求解空间进行单元分割，并用分割单元对障碍空间和自由空间进行描述，再利用基于图的搜索算法，如A*算法[2-3]，在所构建的环境图中搜索有效路径，有利于获得优化路径解。但是，这种方式用于狭窄三维空间内的路径求解时，分割单元的尺寸将直接决定狭窄空间内有效节点的数量、求解成功率与效率。分割单元尺寸过大时，有效节点过少，求解困难；分割尺寸过小时，则存在组合爆炸的情况。

快速扩展随机树（Rapid-exploring Random Tree，RRT）[4-5]是一种随机采样的路径规划算法，特点在于利用随机性来处理C空间而无需对求解空间进行精确计算，因而广泛应用于高维空间下的路径规划问题。但是，由于狭窄空间内产品装配时受到的空间约束较大，使用RRT算法进行装配路径规划时，随机采样点搜索到狭窄空间的概率低，路径树扩展的成功率和效率都有待提高。

针对以上问题，本文结合栅格法与RRT算法的优点改进RRT算法，以待扩展树节点为中心，离散化局部空间，提出两种运动策略及对应的评价指标，引导局部路径的扩展。

本文主要创新点如下。

（1）提出一种局部位移和转动空间的离散化方法，对待扩展树节点附近的局部空间进行离散化设计，为路径树的扩展提供多种备选位姿，以提高路径扩展的成功率与效率。

（2）根据装配运动的难易程度，提出两种运动策略及对应的评价指标，并依据评价指标对备选位姿进行选择。

（3）基于上述局部空间离散化设计及两种运动策略，提出一种改进的快速搜索随机树算法，用于狭窄空间内产品的虚拟装配路径求解。仿真实验表明，此方法在求解成功率和效率方面具有有效性。

1 快速搜索随机树算法

RRT算法的基本原理是通过均匀和随机地搜索状态空间来递增地扩展路径树，直到路径树的叶节点到达终点区域。

它的搜索路径过程主要包括以下步骤。

（1）路径树初始化，即将路径起点（装配起点） (xstar,ystar,zstar)加入路径树中。

（2）路径树扩展。在自由空间内生成随机采样位姿点qrand，遍历树中节点，从而找到与qrand距离最近的节点qnear。从qnear出发，将路径树朝着qrand按照某种运动曲线或运动规律运动一定时间到达一个新的位姿点qnew。若该新位姿点qnew满足碰撞约束要求，则将该点及其局部路径加入路径树中，否则重新进行随机采样，直至路径树扩展成功。

（3）终止判断。若新加入路径树的节点qnew与路径终点(xgoal,ygoal,zgoal)之间的距离小于基础值dth，则路径搜索成功。

2 改进算法设计

在改进算法中，对待扩展树节点附近的局部空间进行离散化设计，并为路径树的局部扩展提供两种策略。每种策略提供多种备选位姿，以提高路径树局部扩展的成功率和效率。

2.1 局部空间离散化设计

产品零部件进行装配时，装配运动既包含移动又包含转动，因此需要从移动和转动两个角度进行局部空间的离散化设计。

以当前路径树待扩展的树节点为中心所构建的局部离散化空间，如图1所示。该局部离散化空间由8个边长为l的正方体单元组成。路径树扩展时，只能从图1中正方体单元的顶点选择新节点。产品移动运动可以选择正方体单元的一条边、一条面对角线或一条体对角线作为下一移动运动路线轨迹。由图1可以看出，与当前待扩展的树节点所相邻的顶点共26个。

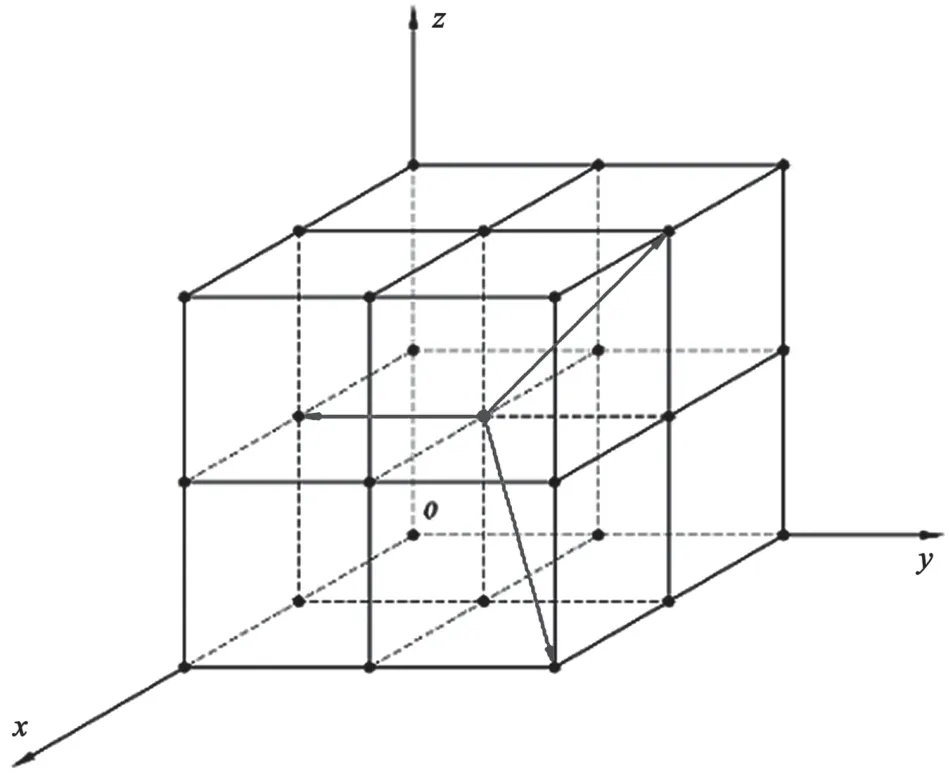
图1 局部位移空间的离散化设计

这种空间的离散化设计与栅格法的不同之处在于，它的计算过程并非在路径搜索开始之前完成，而是在路径搜索过程中进行的，且无需对整个求解空间进行离散化，只需对待扩展路径节点附近的局部空间进行离散化即可。随着路径树的生长，待扩展树节点与障碍物之间的距离发生变化，分割的单元尺寸l也可随之变化。此时，可结合动态步长策略[6]动态地设计单元尺寸。

不同形状的产品绕Z轴转动的离散化设计，如图2所示。相邻姿势之间的转动角度间隔为αz，产品从当前姿势到下一姿势只能选择逆时针转动αz（记为正）或顺时针转动αz（记为负）。

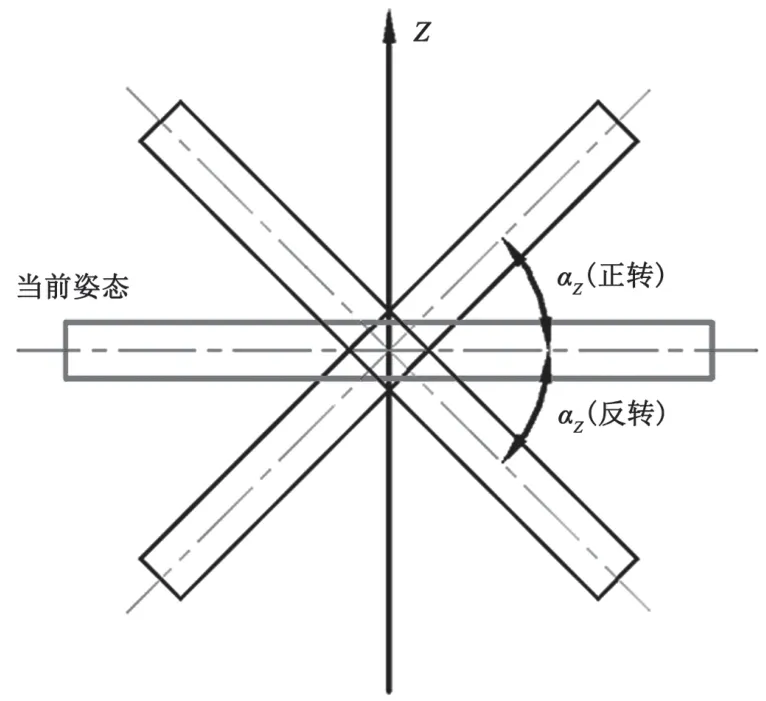
图2 局部转动空间的离散化设计（绕Z轴转动）

假定绕轴X轴和Y轴转动的离散化设计，相邻位姿之间的转动间隔分别为αX和αY。实际装配运动中，产品相邻姿势之间的转动可能是仅绕单轴转动，也可能是绕两轴转动的复合运动，还可能是绕X轴、Y轴、Z轴3轴转动的复合运动。它的转动组合共24种，结合移动的26种情况，路径树的每一步扩展有674种选择，包含仅平移、仅转动和一边移动一边转动。

为降低求解复杂性，本文只考虑相邻位姿之间仅进行平移运动和绕单根轴转动的情况。

2.2 装配路径规划的运动策略与评价指标

为进一步提高求解速度，根据实际装配时操作的难易程度，将路径装配分为仅平移（26种情况）和仅转动（6种情况）两种运动策略，其中将仅平移优先为最高级。进行装配路径规划时，按照优先级的高低顺序进行选择。当高一级的运动策略中的几种情况均不满足要求时，再选择低一级的运动策略。

同一运动策略中，有多种备选位姿，需要根据评价指标对各备选位姿进行评价，并根据评价指标进行排序和选择备选位姿。若该备选位姿通过碰撞检测，则将其加入路径树中，否则将其删除，并更新备选位姿，再依据剩余备选位姿的排序重新选择，直至有新节点加入路径树中。若某一运动策略中的所有备选位姿均不满足要求，则选择低一级的运动策略，并按该策略的评价指标对备选位姿进行评价、排序、选择和检测。

在仅平移运动策略中，从当前位姿至备选位姿均为仅平移运动，且平移距离均为分割单元正方体的边长l，即从装配起点经当前位姿至各备选位姿所产生的移动累计距离一致，但各备选位姿至终点位姿的实际距离不一致。以备选位姿至终点位姿的直线距离为仅平移运动策略的评价指标，备选位姿i评价指标为：

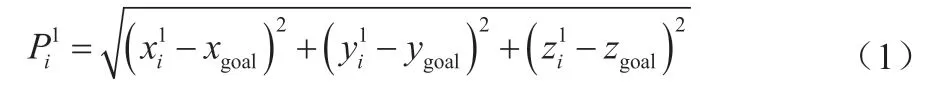
式中：i=1,2,…,26，表示备选位姿编号；(xi1,yi1,zi1)表示备选位姿坐标；(xgoal,ygoal,zgoal)表示终点坐标；Pi1越小，表明与终点越近，有利于加快路径搜索进程。

在仅转动策略中，从当前位姿至备选位姿均为仅转动运动，转动的方向只能是正转或反转，且位姿角度差只能是αX、αY或αZ。仅转动策略中优先选择正转且转动角度最小的备选位姿。若αX、αY或αZ角度值相等，则随机选择。

2.3 改进算法的流程设计

改进算法的流程如图3所示。本算法基于“可拆即可装”的思路[7]，将装配终点设置为路径起点，将装配起点设置为路径终点，求解拆卸路径。它只需将零部件移出产品包围盒即可，无需关注拆卸终点零部件的姿态。获得拆卸路径后，对运动路径进行重新排序，即可获得装配路径。

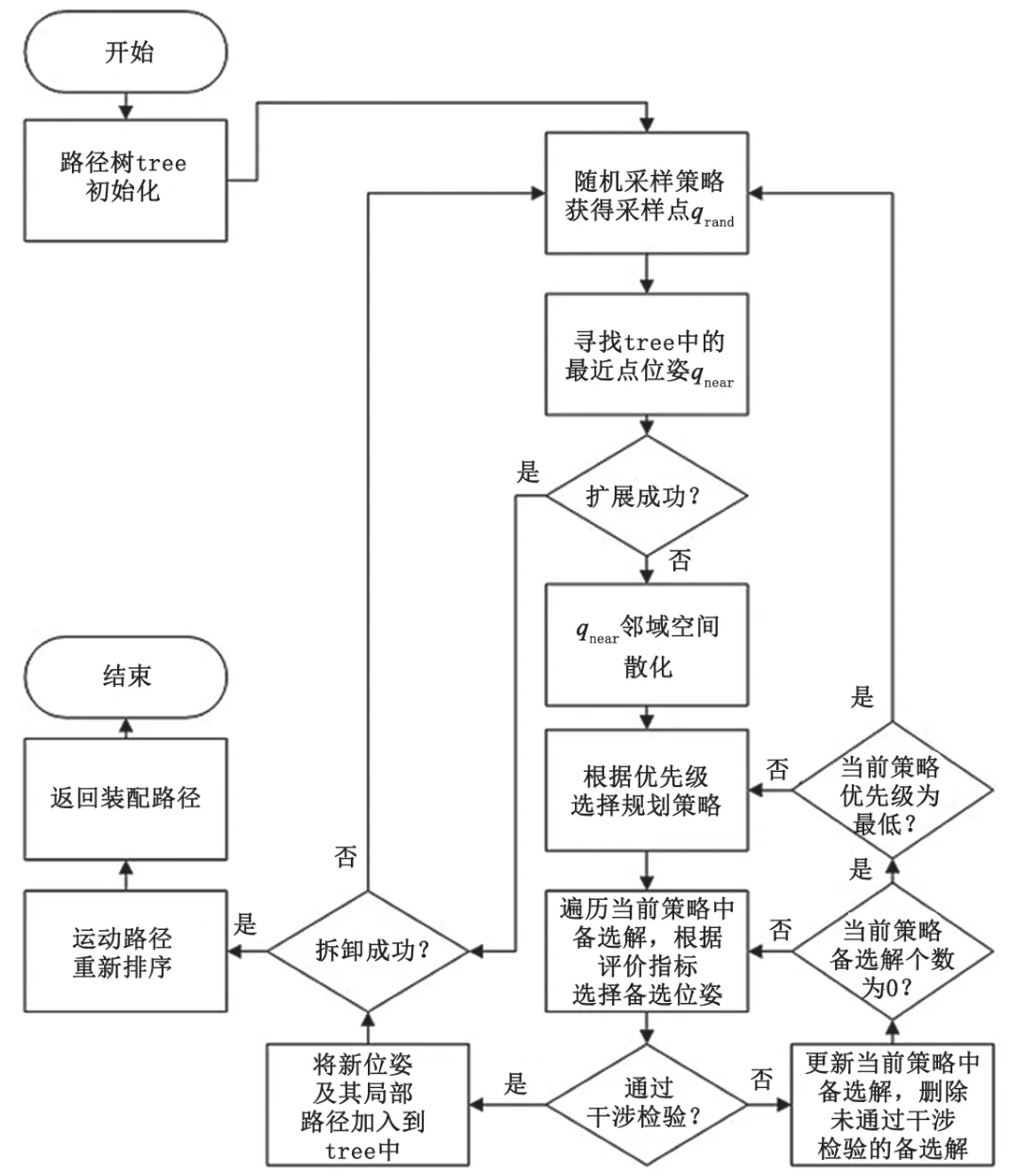
图3 改进算法流程图

进行随机采样时，以一定的概率p选择路径终点为随机采样点。获得随机采样点后，路径树首先朝随机采样点扩展。若路径树朝着随机采样点扩展失败，表明当前树节点在障碍物附近，则启动局部空间离散化，对障碍物附近的局部路径提供多种备选位姿。获得与qrand距离最近的树节点qnear后，随即以qnear现在的位置和姿态为中心进行局部位移和局部转动空间的离散化，获得多个备选位姿。按照运动策略的优先级顺序，先对仅平移策略中的备选位姿进行评价、排序、选择及碰撞干涉检验，直至路径树局部扩展成功。若仅平移策略中的备选位姿均不满足要求，则对仅转动策略中的备选位姿进行评价、排序、选择及碰撞干涉检验，直至路径树局部扩展成功。若仅转动策略中的备选位姿仍不满足要求，则重新进行随机采样点的选择，并重复以上过程，直至有备选位姿加入路径树，完成一次扩展树的过程。路径树多次扩展成功，直至扩展到拆卸路径终点附近，拆卸路径搜索过程结束。路径节点重新排序后，返回从装配起点至终点的路径。

3 仿真验证与结果分析

为验证所提出方法的有效性，对引擎活塞杆帽装配路径进行规划仿真实验。装配起点与终点如图4所示，其中装配终点附近约束强烈，是典型的狭窄空间下的装配路径规划问题。

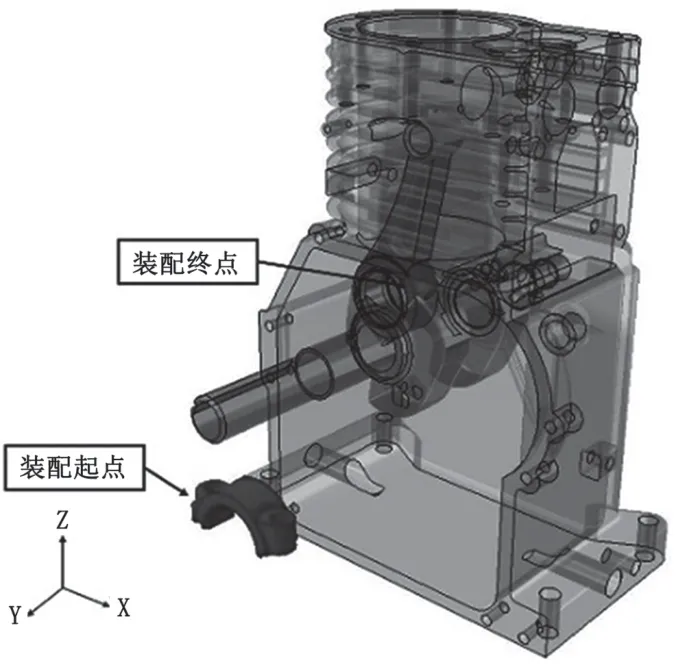
图4 活塞杆帽装配路径规划的起点与终点

将本文算法与RRT算法和Biased-RRT[8]算法比较后，可得所提方法适用于狭窄空间内复杂产品的装配路径规划问题。在仿真实验中，三维空间在OX、OY和OZ这3个方向上的范围均为0～500 mm，其他仿真参数如表1所示。

表1 仿真参数设置表

3种算法在解决如图4所示的装配路径问题时的表现如表2所示。由于RRT算法具有随机性，故表2中成功率指的是算法重复执行100次时搜索成功次数与总次数的比值。搜索时，设定每次执行时最大允许迭代次数为100，在允许的迭代次数内返回装配路径即表示此次搜索成功，超过迭代次数还未返回路径则表明路径搜索失败。

表2 算法表现对比表

从表2可知，改进算法找到路径的成功率和效率最高。相比于RRT算法和Biased-RRT算法，本文提出的改进算法先朝向随机采样点扩展，若扩展不成功再进行局部离散化，为局部路径的扩展提供了多种选择。只要存在可扩展点，则该局部路径即可扩展成功。这一策略有利于提高狭窄空间中路径扩展的成功率和效率。

改进算法获得的装配路径，如图5所示。该装配路径是由所获得的拆卸路径各节点重新排序获得，而拆卸路径规划过程中只要零件拆出产品包围盒即可，无需保证拆出时的姿态与拆卸终点（装配起点）的姿态一致，故图5中装配起点处的局部运动姿态有较大改变，而这一局部运动在开阔区域完成，认为是可接受的。

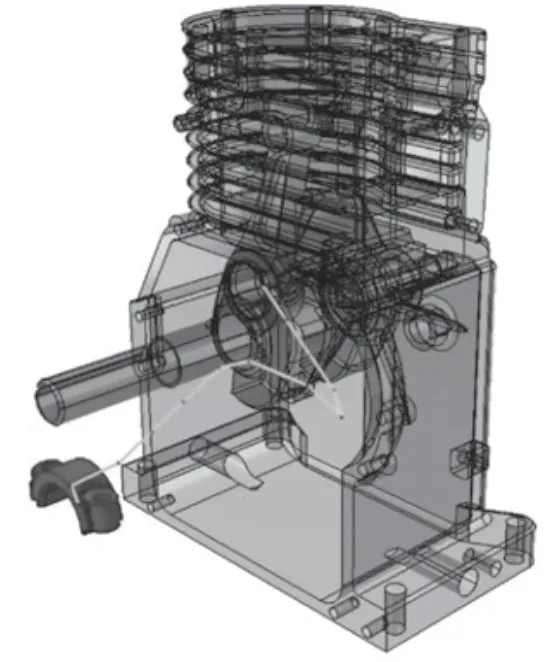
图5 改进算法所生成的路径

4 结语

针对狭窄空间中复杂产品装配路径规划成功率和求解效率低的问题，提出一种改进的快速搜索随机树算法。此方法将路径节点的局部空间离散化，提供多个备选位姿，提出两种运动策略及对应的评价指标，提高了路径扩展的成功率与效率。仿真实验结果表明，此方法可有效解决狭窄空间中的装配路径规划问题，并可提高求解成功率与效率。