车载稳定隔振平台的惯性参数辨识方法研究
田体先 韩 意 马玉浩 鲁吉林 赖 震
(1.武汉科技大学,武汉 430081;2.陆军装备部装备项目管理中心,北京 100007; 3.陆军装备部驻北京地区军事代表局驻临汾地区军事代表室,侯马 043000)
特种车辆被应用于各种复杂场景,如战场环境下的全地形救护车。救护车辆行驶过程中会受到来自地形和车速变化的影响,且外部加速度的扰动随机性较强,对车辆的冲击较大。振动和冲击会对伤员造成二次伤害,有必要采取措施隔离和缓冲其在动态环境中所受到的振动[1]。因此,根据医疗救护隔振平台的使用要求进行相应的隔振设计具有重要意义[2]。
车载隔振平台的类型很多,按减振机构的控制方式一般可分为被动隔振平台、半主动隔振平台和主动隔振平台。6自由度并联机构作为主动隔振平台,具有精度高、承载能力大的优点。例如:哈尔滨工业大学研制的基于Stewart机构的八作动器隔振平台[3],采用气压作动器的方式提供主动隔振能力,且阻尼器与弹簧并联,提高了隔振平台的稳定性和可靠性,增加了系统的刚度和承载能力[4]。
2 6自由度隔振平台动力学
6自由度隔振平台结构示意图,如图1所示。它由1个上平台、1个下平台以及6个相互独立的电动缸组成。6个支腿通过虎克铰与上下平台相连[5]。该机构具备空间6个自由度的运动能力,定义上平台重心Oa、下平台重心Ob,建立动坐标系Oaxayaza和固定坐标系Obxbybzb。上平台铰点中心和下平台铰点中心分别用ai和bi(i=1,…,6)表示。并联机构的空间位姿采用广义坐标p=[c,β]来表示,其中平移表示为c=[x,y,z]T,转动姿态采用欧拉角表示β=[φ,θ,ψ]T,并按照Z-Y-X的顺序实现转动。
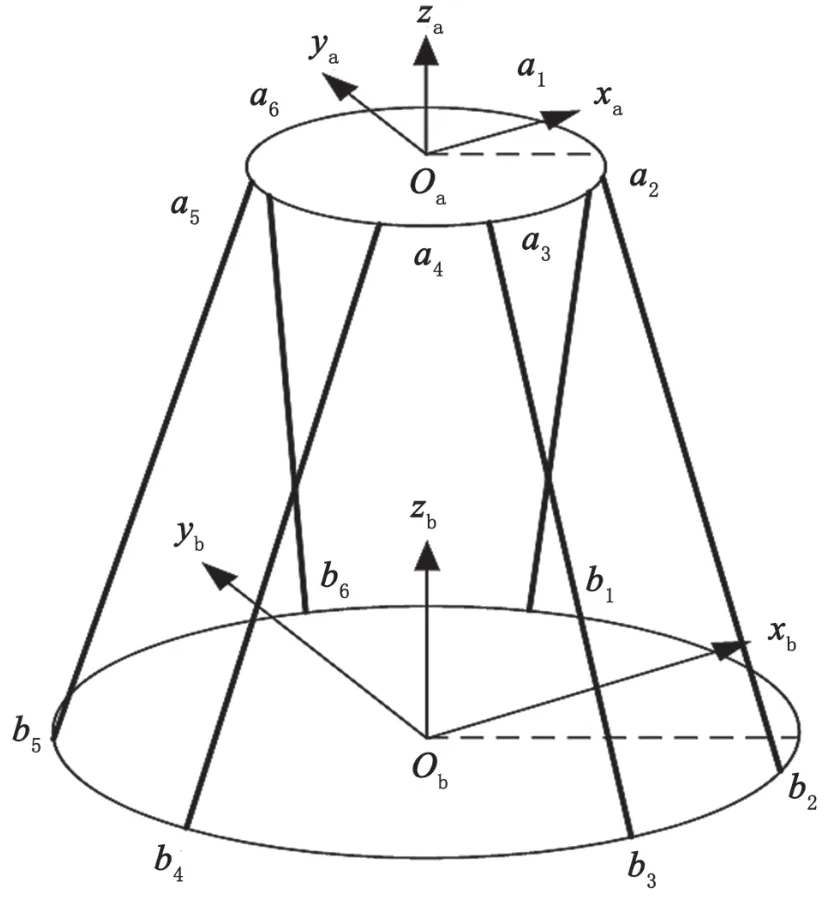
图1 6自由度隔振平台结构
2.1 惯性参数辨识模型
并联平台的动力学方程表述为:

式中:mp(p)为上平台质量矩阵;Cp(p p˙)为哥式力/向心力系数矩阵;Gp(p)为重力项矩阵;J1,p(p)为并联平台雅可比矩阵;支腿力Fa为支腿驱动力。
在电动6自由度隔振平台中,支腿力由电动缸来提供。对电动缸进行动力学分析,建立以电机转矩为输入、支腿出力为输出的传递函数模型,如图2所示。

图2 支腿动力学传递函数框图
2.2 惯性参数辨识方法
当并联平台以正弦信号运动时,分析驱动力信号。由动力学方程式(1)可知,驱动力可分解为惯性力、科氏力、向心力、阻尼力和重力。其中,惯性力和阻尼力为与位姿信号频率相同的基频分量,科氏力和向心力为高频分量,重力项为常量。因此,可分离惯性力中的基频分量,从而辨识惯性参数。
采集信号时,将系统激励力改写为傅里叶形式,并提取其中的基频分量构建辨识方程,为:

式中:Fs,c为激励力信号的基频分量系数矩阵。
将6次的激励数据按顺序排列,构成辨识方程为:

式中:W为速度与加速度基频分量矩阵;H为力信号基频分量矩阵。
对位姿信号正弦幅值分量S和力信号基频分量H的计算采用最小二乘法,对式(3)进行求解,即可完成惯性参数的辨识。
3 惯性参数辨识仿真研究
实验采用Adams和Matlab联合仿真。在Adams中搭建好模型并设置相关参数,然后生成联合仿真Adams_sub模块。在Matlab中建立并联机构上平台参考轨迹模块、位移反解模块以及增益模块,仿真结构模型如图3所示。

图3 仿真模型
图3中:上平台参考轨迹模块负责对并联平台6个自由度产生激励;反解模块将上平台的位姿反解为6个电缸的位移。仿真结束后,在Adams中提取电动缸的转矩、位移等必要参数,带入辨识算法中进行计算。辨识结果如表1所示。

表1 辨识结果
从表1可以看出,并联平台质量辨识误差小于2%,转动惯量辨识误差小于7%,辨识值与实际值之间的误差很小,证明采用转矩辨识结果可靠、精确。
4 结语
本文推导了隔振平台支腿动力学模型,建立了并联机构隔振平台的惯性参数辨识方程,提出了一种采用电机力矩信息构造的适用于电动6自由度隔振平台的惯性参数辨识方法,并对提出的辨识方法进行了仿真研究。结果表明,该方法可准确获得平台惯性参数。

