虚拟电流注入法在线补偿转子位置估算误差

彭 威，乔鸣忠，蒋 超，高键鑫，卢希浩

(海军工程大学 电气工程学院， 湖北 武汉 430033)

永磁同步电机的高精度控制需要电机实时转子位置，通常采用旋转变压器等位置传感器进行检测[1]，但对于舰船使用的机桨一体化装置，位置传感器的安装和维护困难。无位置传感器控制成为解决这一问题的一种技术手段。

零速和低速时电机反电动势低，采用基于反电动势的观测器方法[2]难以准确估算转子位置，所以通常采用高频注入法。高频注入法通常又分为旋转高频注入法[3-4]和脉振高频注入法[5]。旋转高频注入法需要电机有一定的凸极率，而脉振高频注入法可适用于凸极率很小甚至表贴式电机。但旋转高频注入法易于实现[6]，使其成为研究的热点。

旋转高频注入法关键技术在于通过解调高频响应电流获取转子位置。简化电机高频响应模型，以及解调过程中使用滤波器都可能导致估算的转子位置与真实值出现偏差。通过理论推导可以计算出忽略定子电阻导致的转子估算误差量[7-8]来进行定量补偿，但电机运行过程中电感会随磁路饱和程度变化而变化[9]，李峰等提出了一种分步动态电感辨识方法并给出了相应的转子位置误差补偿方案[10]。邵俊波推导了忽略交叉耦合导致的误差，采用线性拟合误差的方法来进行补偿[11]。

随着电机转速的上升，滤波器导致的误差会更加明显，成为电机低速运行时估算位置误差的主要来源。廖军等利用多个同步轴系变换结合高通滤波器取代带通滤波器和带阻滤波器[12]。Kim等[13]用全通滤波器代替带通滤波器和低通滤波器减小相位延时带来的误差。刘景林等通过对高频电流正、负序分量的相角差利用最小二乘估计，得到了较高精度的转子位置[14]。在电机处于零速时，利用正序电流的偏差量来补偿转子初始位置估算误差[15-16]。文献[17]研究了注入旋转电压的频率、幅值等对于电机无位置传感器矢量控制性能的影响。在转子位置解调环节，利用扩展状态观测器取代比例积分(Proportional Integral, PI)观测器也能改善转子位置估算效果[18]。黄守道等用两个相同的一阶低通滤波器串联来实时获取由于采用一阶低通滤波器带来的相移[19]。文献[20-21]指出，通过在脉振高频脉振注入法中构造虚拟坐标系取代带通滤波器和PI调节器，可减小转子位置估算误差和提高系统鲁棒性。

本文提出一种虚拟电流注入法补偿旋转高频注入法因低通和带通滤波器导致的误差。基于估算的转速，构造与负序电流频率相同的虚拟电流，该电流采用与负序电流完全相同的解调环节。利用虚拟电流解调出的位置与构造的位置的差值补偿估算的转子位置。由于滤波器对电流相位的影响仅与电流频率有关，当估算的转速为电机真实转速时，虚拟电流注入补偿法将能消除滤波器导致的误差。

1 虚拟电流注入法在线补偿误差的机理

1.1 旋转高频注入法转子位置信息解调

旋转高频注入法是在αβ坐标系下给电机注入一个频率远高于电机基波频率但低于开关频率的旋转电压。

(1)

式中，uαh、uβh分别为注定电压在α轴和β轴上的分量，ωh、uh分别为注入高频电压的角频率和幅值。

将电机简化成纯电感模型，得到αβ坐标系下的高频响应模型。

(2)

式中：L0=(Ld+Lq)/2,L1=(Ld-Lq)/2，Ld、Lq分别为直轴和交轴电感；iαh、iβh分别为α轴和β轴上的高频响应电流分量；p为微分算子；电机转子位置θe=ωet+θ0，θ0为电机初始位置，ωe为电机基波电角速度。

结合式(1)、式(2)，高频响应电流可表示为：

(3)

式中，Iph、Inh分别为高频响应电流正、负序分量的幅值。

(4)

可以看出高频响应电流负序分量中含有转子位置信息，对负序分量进行解调来得到转子位置信息。解调过程如图1所示。

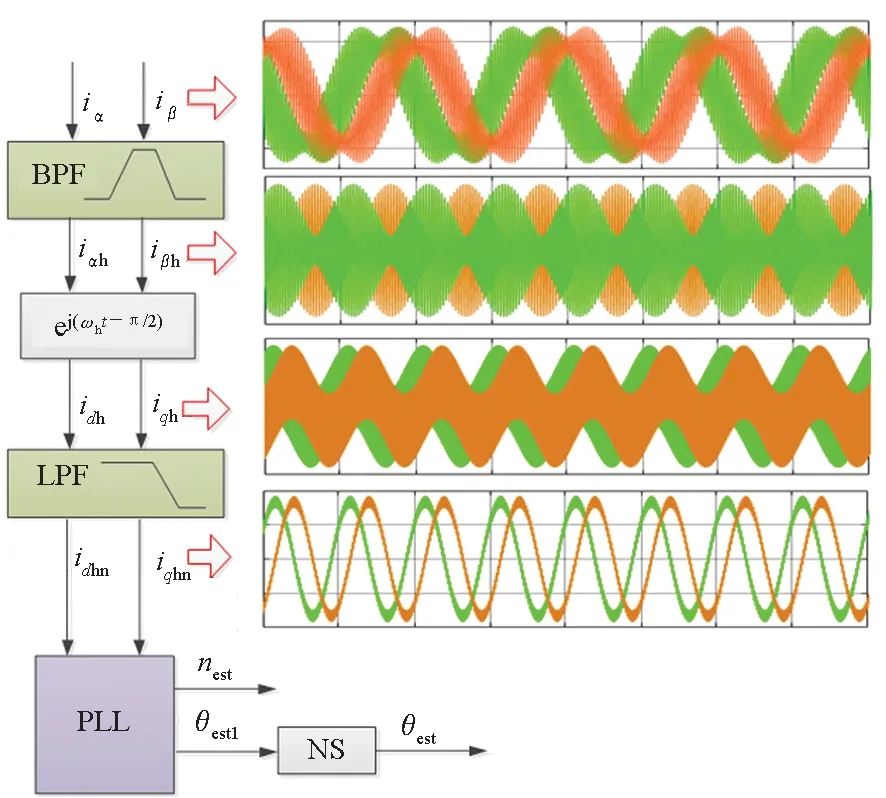
图1 高频响应信号解调原理图Fig.1 Demodulation diagram of high frequency response signal

若忽略滤波器对于电流相位的影响，带通滤波器(Band Pass Filter，BPF)滤掉电机基波频率的低频分量和开关频率的高频分量，只留下注入法产生的高频响应电流iαh、iβh，经过角速度为-ωh的同步轴系滤波，得到电流idh、iqh:

(5)

此时的正序分量为高频交流量，负序分量为角速度为2ωe的低频交流量。若通过低通滤波器(Low Pass Filter，LPF)能完全滤除正序高频分量，剩下负序低频分量idhn、iqhn。

(6)

idhn、iqhn通过锁相环和转子磁极判断[13-15]可以得到估算的转速nest和转子位置θest。关于磁极判断的方法已有较多研究，这里不做重点论述。

1.2 虚拟电流注入法在线补偿转子位置误差

在高频响应信号解调过程中，用到带通滤波器和低通滤波器会产生转子位置估算误差，提出虚拟电流注入法来同时补偿两种滤波器带来的误差，如图2所示。

图2 虚拟电流注入法信号解调原理图Fig.2 Demodulation diagram of virtual current injection method

虚拟注入电流是基于估算的电机速度nest，利用数字信号处理器(Data Signal Processor, DSP)等处理器构造一组高频虚拟电流信号：

(7)

ωest是电机估算转速nest所对应的电角速度。iαi、iβi只参与解调过程，不会对空间矢量调制或电机的实际运行带来影响。先估算转速和转子位置再进行补偿，时间轴ti的起始点为补偿开始实施的时刻，与t不同。实际电流和虚拟电流采用相同采样频率。高频响应电流的正序分量角频率ωh，负序分量的角频率为-(ωh-2ωe)，虚拟电流角频率为-(ωh-2ωest)。实际采样电流和虚拟电流通过相同的高通、同步轴系和低通滤波器以及锁相环解调。

不考虑简化电机模型等带来的影响，带通滤波器对于ωh、(ωh-2ωe)、(ωh-2ωest)三个频率点处的幅值衰减为K0倍和K1、K2倍，相位滞后分别为ψ0和ψ1、ψ2，高频响应电流和虚拟注入电流经过带通滤波器后变为：

(8)

(9)

通过同步轴系滤波器后电流变为：

(10)

(11)

若经过低通滤波器后，正序电流分量幅值衰减为零，负序电流与虚拟注入电流幅值衰减和相位延时分别为K3、K4，ψ3、ψ4，滤波后得到的低频交流量为：

(12)

(13)

通过锁相环可以得到估算的电机转子位置θest和虚拟注入信号包含的位置θesti分别为：

(14)

(15)

而构造的虚拟注入电流信号中ωestti为已知量，故可得到对虚拟电流解调环节导致的位置误差为：

(16)

用Δθi对估算的电机转子位置进行补偿，补偿后的转子位置为：

(17)

若估算的电机转速为实际的电机转速，则高频响应负序电流角频率-(ωh-2ωe)与-(ωh-2ωest)相等，而相同滤波器对频率相同的电流相位影响相同，此时ψ1=ψ2、ψ3=ψ4，采用虚拟注入法可以完全消除使用滤波器导致的误差。

2 影响虚拟注入法误差补偿效果的因素分析

虚拟注入信号与负序响应电流频率相同，即估算转速与真实转速相同时，理论上虚拟注入法能完全消除滤波器导致的位置误差。但注入高频电压会使电机转速出现波动，而受正序电流的影响，估算的转速也出现波动，最终导致虚拟注入信号频率与负序电流频率不同。故有必要对上述因素对补偿效果的影响进行分析，采取合理措施保证虚拟注入法的补偿效果。

2.1 高频响应电流引起电机转速波动

电机稳态下，基波电流产生的电磁转矩使电机达到转矩平衡，而高频响应的脉动转矩会导致电机转矩波动。将式(3)变换到基波旋转坐标系下，得到dq轴电流为：

(18)

结合式(4)，可将高频响应电流产生的电磁脉动转矩简写为：

(19)

式中，pn为电机极对数，ψf为转子磁链。结合式(4)可知，脉动转矩作用于电机转动惯量J产生机械角加速度。

(20)

而脉动转矩频率为(ωh-ωe)，在一个脉动周期内对机械角加速度积分，易求出电机机械角速度变化量为：

(21)

由式(21)可知，提高注入电压频率可降低转矩脉动导致的转速波动量，而电机转速上升会导致转速波动量上升。但提高注入频率，高频响应电流变小，会需要更高的电流采样频率和电流采样精度，加大电流检测的难度。

借助仿真进一步探讨高频响应电流引起的转速波动大小，矢量控制下当注入频率取500 Hz，4对极电机运行在50 r/min和150 r/min时的实际转速波动如图3所示。

图3 高频响应电流引起电机转速波动Fig.3 Motor speed fluctuation caused by high-frequency response current

转速为150.0 r/min时的波动频率比50.0 r/min时小，转速波动要大于50.0 r/min，但都在0.8 r/min以内，对应的负序电流频率波动在0.1 Hz以内。

2.2 高频正序响应电流引起估算转速波动

负序响应电流与正序响应电流之比为(Lq-Ld) ∶(Ld+Lq)，负序电流在凸极率不高时会明显比正序电流小。通过同步坐标轴系变换后正序电流变为两倍注入频率的交流量，而原来负序电流变为两倍基波频率的交流量。低通滤波器LPF1首先要具有一定带宽能保证不同转速下负序电流幅值不衰减以被锁相环解调，其次还要能充分滤除正序电流，否则会导致估算转子位置出现波动。

若采用截止频率为450 Hz、550 Hz的二阶巴特沃斯带通滤波器和截止频率为60 Hz的二阶巴特沃斯低通滤波器，当注入频率取500 Hz，4对极电机运行在120 r/min时的估算电机转速和实际电机转速波动量如图4所示。估算转速以两倍注入频率波动，估算的转速波动量远大于转矩脉动导致的电机实际转速波动量，引起的虚拟注入信号频率的波动接近7 Hz。

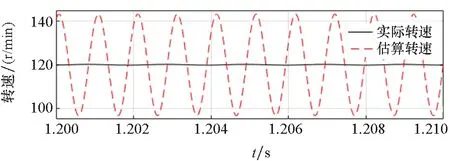
图4 估算转速与实际转速波动量Fig.4 Fluctuations of the estimated speed and actual speed

2.3 提高虚拟注入法误差补偿效果的措施

通过上述分析比较可知，未能完全滤除正序电流导致的估算转速波动是影响虚拟注入法补偿效果的主要因素，而高频转矩脉动导致的影响较小，减小转矩脉动会导致电流检测和采样难度增加，故主要从消除虚拟注入电流频率波动来改善补偿效果。

正序电流和负序电流都为交流量，要想保证低通滤波器对负序电流的带宽的同时完全滤除正序电流，会导致滤波器设计过于烦琐，不便于DSP实现。

采用一个低通滤波器(图2中的LPF2)对波动转速信号进行滤波，得到稳定的转速用于构造虚拟电流信号。LPF2作用对象为直流量，不需要考虑带宽，通过LPF2完全滤除估算转速信号的波动量更容易实现。

采样频率为10 kHz，LPF2设计为一阶巴特沃斯滤波器，截止频率为10 Hz。通过FDATool可知，LPF2对于(ωh-ωe)的估算转速高频波动量的幅值增益约为-60 dB，能消除用于误差补偿的估算转速的高频波动量。

电机工况改变到再次进入稳定的过程中，电机转速都会出现瞬时的变化后稳定在指令值。通过阶跃信号来替代这种瞬时的转速变化来进行分析。阶跃信号通过LPF2后幅值经过约0.05 s上升到1，而电机实际的转速变化斜率不可能达到阶跃响应的斜率，这意味着在实际工程电机转速变化时，LPF2对于电机转速变化的延时将在0.05 s以内。在这0.05 s内，虚拟注入法补偿的精准度会受到影响。但由于LPF2仅用在估算转子位置误差补偿，LPF2对于转速变化的延迟不会影响基本的转子位置解调和电机运行。

3 仿真研究和实验验证

为了验证所提出的转子位置估算误差补偿法的正确性和效果，搭建了一套永磁同步电机的矢量控制仿真模型，电机和变频器部分参数如表1所示。

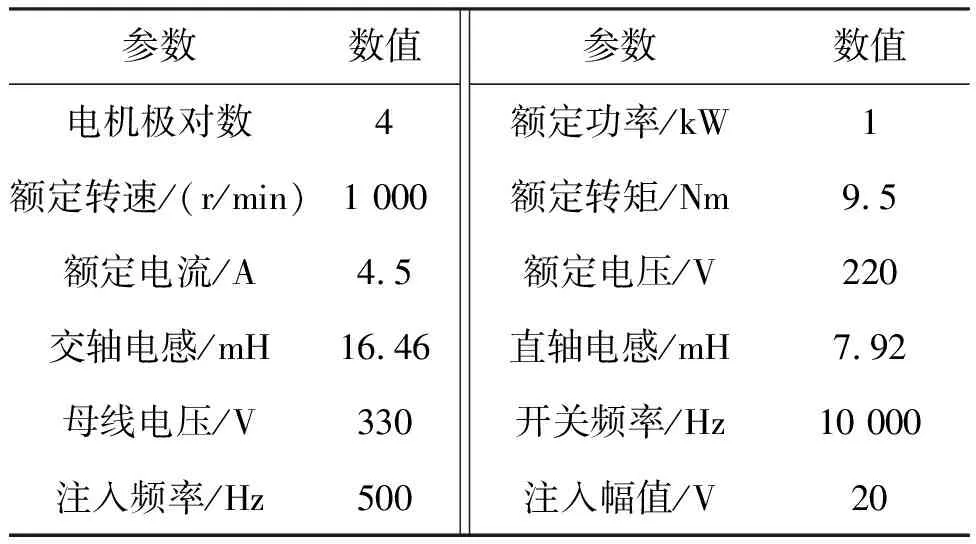
表1 三相永磁同步电机控制平台参数

综合考虑滤波器对正序电流的幅值的衰减效果和电机运行区间以便于处理器快速运算。实际电流解调采用截止频率为450 Hz和500 Hz的二阶带通滤波器BPF，和截止频率为60 Hz的低通滤波器LPF1。

利用MATLAB里的FDATool工具可以分析出电机处于不同转速时滤波器导致的电流相位延迟和估算的转子位置误差，如表2所示。

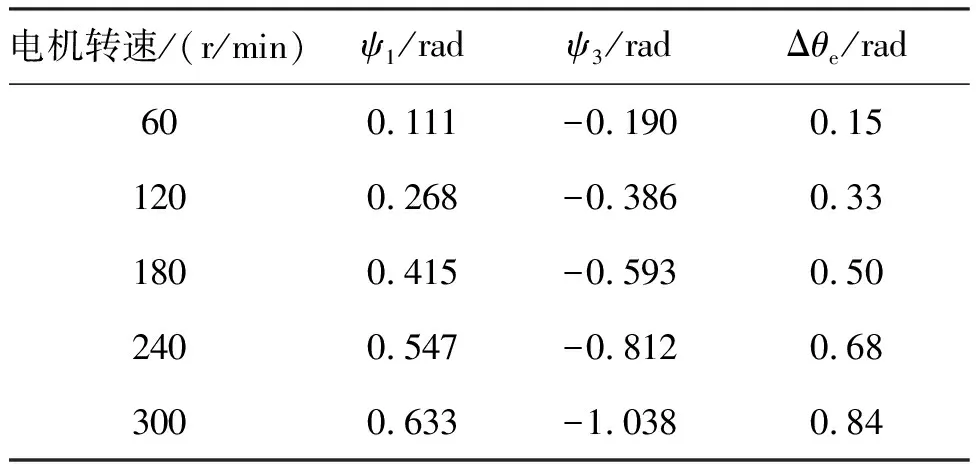
表2 电机不同转速下滤波器导致的转子位置估算误差Tab.2 Rotor position estimation error caused by filters at different speeds

当电机空载运行在60 r/min和120 r/min时，在0.5 s处突加负载仿真波形如图5、图6所示。从图5、图6可以看出，突加转矩负载，电机转速波动后能迅速稳定，高频电流解调用到的滤波器会使估算的转速变化滞后于实际转速变化。采用虚拟注入法补偿估算的转子位置后误差得到了明显减小，补偿后估算的转子位置曲线与实际转子位置曲线基本重合。

(a) 电机实际转速和估算转速(a) Actual speed and estimated speed of motor

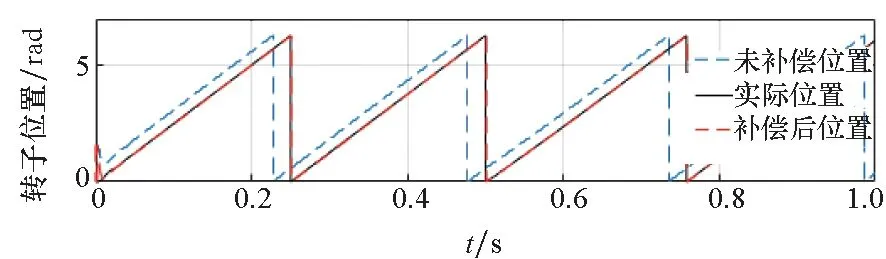
(b) 转子位置(b) Rotor position

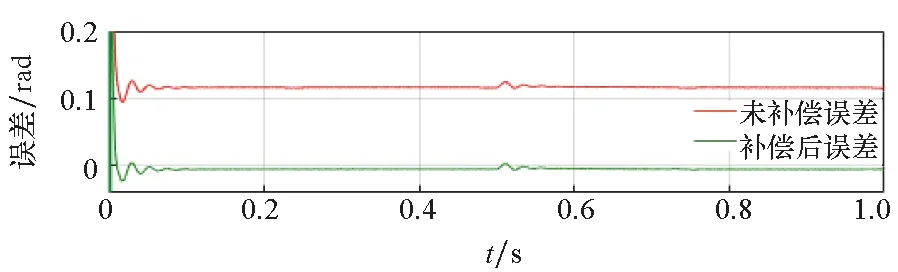
(c) 转子位置误差(c) Rotor position error图5 60 r/min转速突加负载仿真波形Fig.5 Simulation waveforms at 60 r/min with sudden load

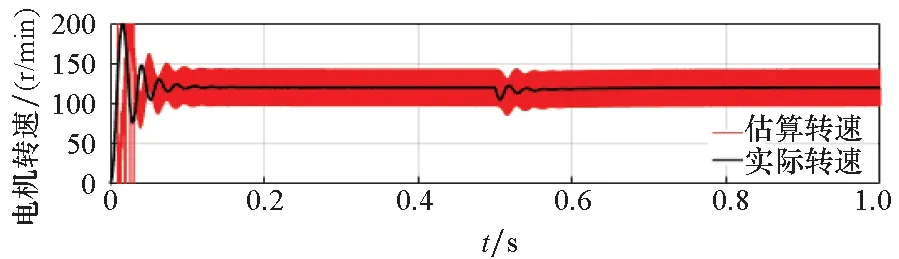
(a) 电机实际转速和估算转速(a) Actual speed and estimated speed of motor

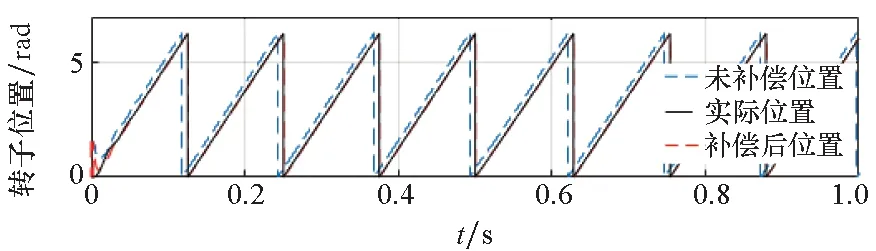
(b) 转子位置(b) Rotor position

(c) 转子位置误差(c) Rotor position error图6 120 r/min转速突加负载仿真波形Fig.6 Simulation waveforms at 120 r/min with sudden load

由于虚拟注入用到的是经过低通滤波器LPF2后的估算转速，为定值，故突加负载不会导致虚拟注入电流频率波动，整个过程补偿量基本为定值。

对电机运行在180 r/min、240 r/min、300 r/min时采用虚拟电流注入法的补偿效果进行仿真，对误差补偿量大小、补偿后误差大小以及表2中分析的滤波器理论误差大小进行比较，如图7所示。

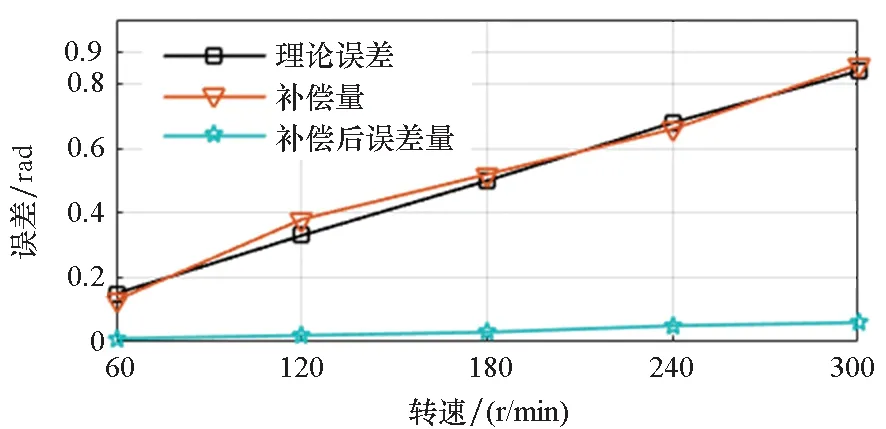
图7 不同转速下的补偿效果Fig.7 Compensation effect at different speeds

从图7可以看出，在不同转速下虚拟注入法得到的补偿量与理论误差吻合，且补偿后转子位置误差明显减小，说明该补偿方法能基本消除由滤波器导致的转子位置误差。

搭建如图8所示的实验平台，进一步验证虚拟电流注入法对估算转子位置误差的补偿效果。

图8 实验平台Fig.8 Experiment platform

两台永磁同步电机参数相同，永磁同步电机参数和变频器参数与表1相同。DSP28335内部变量信息通过串口发送给电脑显示，实际转子位置和估算的转子位置等信息通过数模转换成电压信号，利用示波器采集。

转速为60 r/min和120 r/min时突加负载的实验波形如图9、图10所示。从图9和图10可以看出，电机在加负载前后转速稳定时，通过虚拟注入法能有效减小位置估算误差。在加负载后电机转速变化的过程中，滤波器LPF2对电机瞬间的速度变化有延迟，在延迟时间内补偿精度会受到影响，但LPF2的使用能增加电机稳态时转子位置误差补偿的精度。两种工况下电机处于稳态运行时，补偿后的估算转子位置误差相比未补偿时均能减小77%以上。

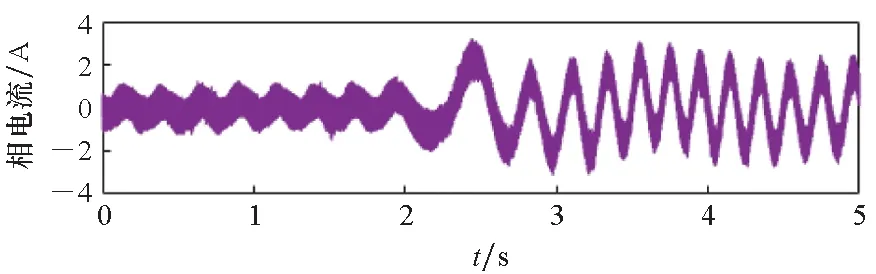
(a) 电机A相电流(a) A-phase current of motor

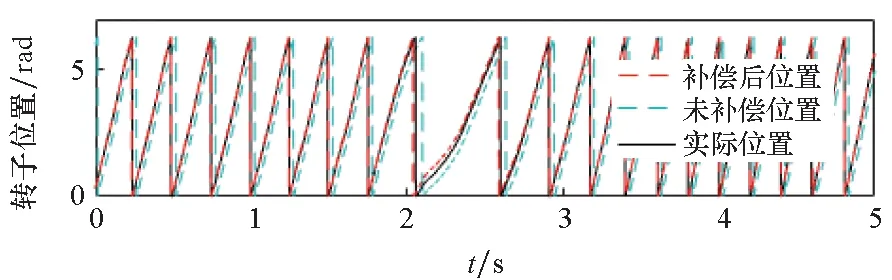
(b) 转子位置(b) Rotor position

(c) 转子位置误差(c) Rotor position error图9 60 r/min转速突加负载实验波形Fig.9 Experimental waveforms at 60 r/min with sudden load

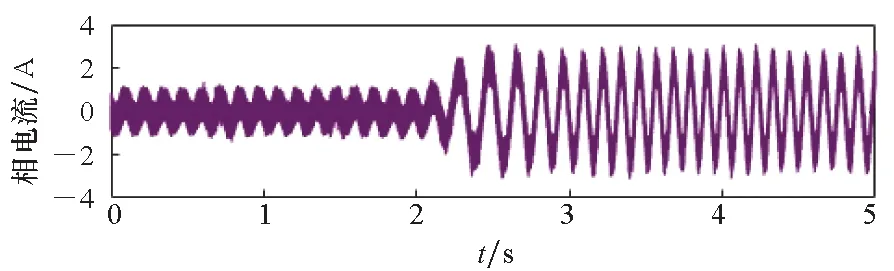
(a) 电机A相电流(a) A-phase current of motor

(b) 转子位置(b) Rotor position

(c) 转子位置误差(c) Rotor position error图10 120 r/min转速突加负载实验波形Fig.10 Experimental waveforms at 120 r/min with sudden load

仿真用到的电机模型没有考虑电机交叉饱和的影响，而实验在带载时尚未对交叉饱和带来的误差进行补偿，所以采用虚拟注入法补偿后实验转子位置误差稍大于仿真时的误差。

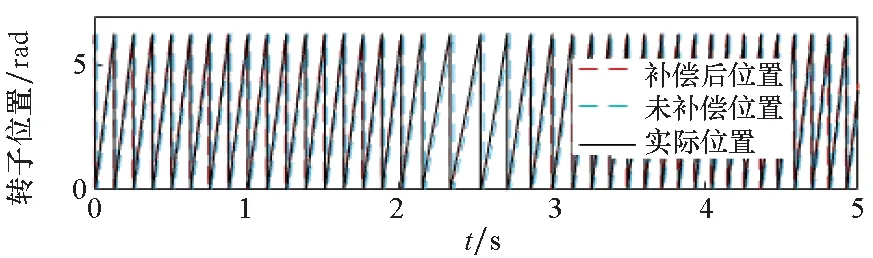
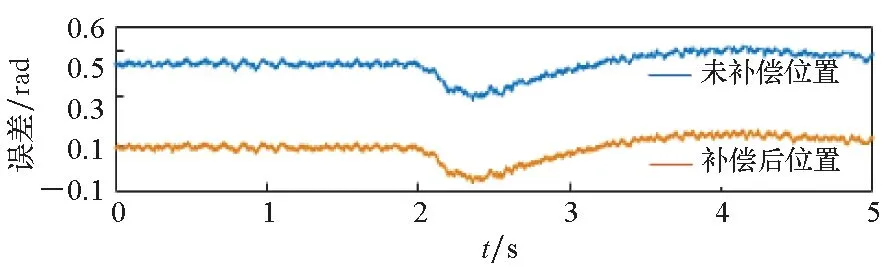
电机空载状态下转速由60 r/min突增到120 r/min时的相关波形如图11所示。在转速增加的过程中，所提补偿方法也起到了明显效果，稳态平均误差在0.1 rad以内，转速变化时的补偿效果比稳定时略差。

但电机大多时候处于稳态，使用LPF2能避免补偿受正序响应电流的干扰，总体上提高电机控制的精度和效率。

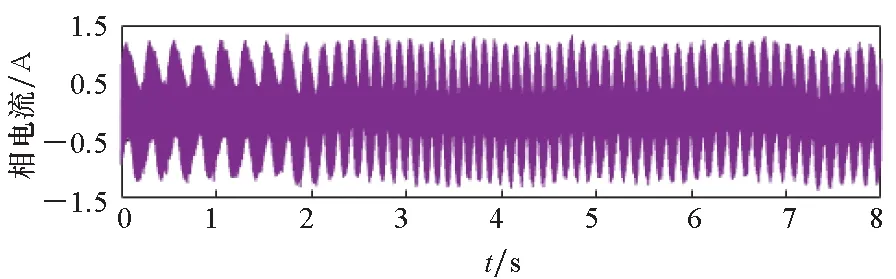
(a) 电机A相电流(a) A-phase current of moto

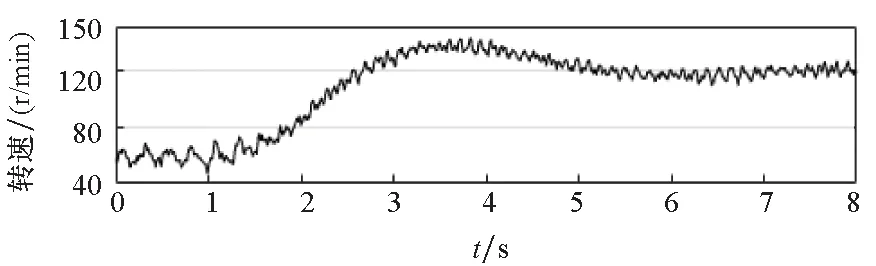
(b) 电机实际转速(b) Actual motor speed

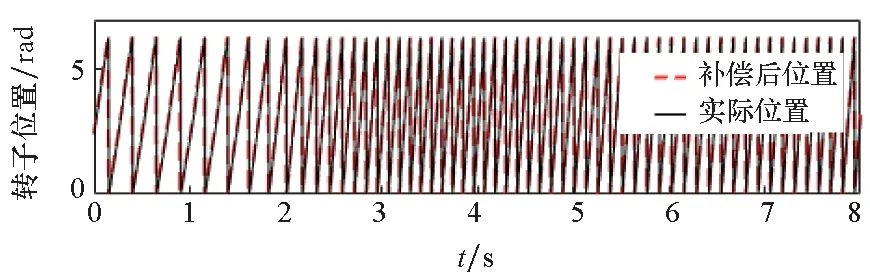
(c) 转子位置(c) Rotor position

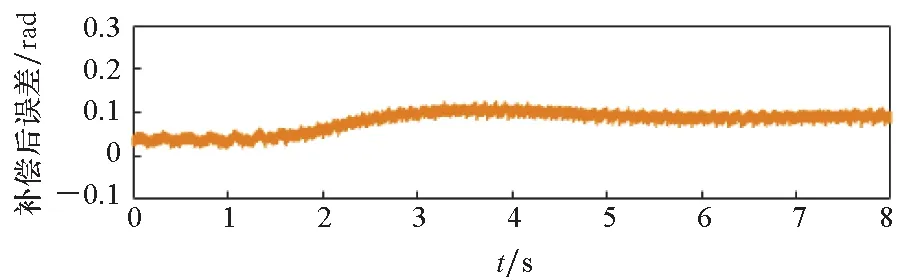
(d) 补偿后的转子位置误差(d) Rotor position error after compensation图11 转速突增实验波形Fig.11 Experimental waveforms with speed increasing

4 结论

本文结合理论推导阐明了虚拟电流注入法补偿转子位置误差的机理，分析了会影响虚拟注入法补偿效果的因素和改善方法，利用仿真和实验对所提补偿方法进行了验证，得到如下结论：

1) 利用虚拟注入法能基本消除电机稳态运行时由滤波器导致的转子位置估算误差，实验的几种工况下采用该方法能使估算的转子位置误差减小77%以上。

2) 使用低通滤波器LPF2可以避免正序响应电流对补偿效果的干扰，提高稳态补偿效果。LPF2对于电机转速变化延迟在0.05 s内，延迟期间误差补偿精度会受到影响，但不会影响电机正常运行。