几何折叠综述
栗菲旋,孙红岩,孙晓鹏,2
1(辽宁师范大学 计算机与信息技术学院计算机系统研究所,辽宁 大连 116029)
2(北京邮电大学 智能通信软件与多媒体北京市重点实验室,北京 100876)
1 引 言
近年来,几何折叠已经成为计算机图形学领域中的研究热点,在工业结构设计[1]、机器人设计[2]、医疗器械设计[3]、生物模拟[4]和航空航天[5]等工程领域应用广泛.本文针对近年来几何折叠领域的相关算法和理论梳理分类,根据折叠的对象不同,将几何折叠技术分为杆折叠(1D)、平面折叠(2D)和三维折叠(3D)3类,分别介绍各算法思路和特点.最后从3个应用领域介绍几何折叠技术的应用情况,总结发展趋势和潜力,为未来的研究工作提供方向.
2 背景介绍
三维模型的几何折叠是指折叠对象从无组织的通用状态开始,到结构化的折叠状态结束的连续运动过程.根据折叠对象不同,可以将几何折叠技术分为3类:杆折叠、平面折叠和三维折叠,如图1所示.通过整理近年来几何折叠的相关文献,本节分别介绍3类几何折叠的背景.
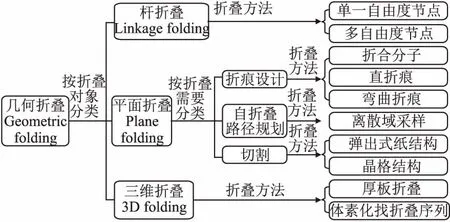
图1 几何折叠分类图
2.1 杆折叠
杆折叠基于平面连杆结构[6],通过其活动的关节在不自交的约束下进行折叠运动,多应用在机器人手臂[7]和蛋白质折叠[8]中.平面连杆结构是位于平面中的固定长度的一维段的集合,这些段在其端点处连接以形成连接的图(如图2所示).端点处统称为关节,关节允许360°旋转.在将一个或多个关节固定到平面上的情况下,任何特定的自由关节的运动都会受到连杆结构的限制.
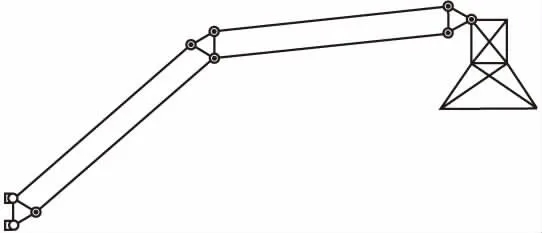
图2 平面连杆结构[6]
2.2 平面折叠
平面折叠是指该折叠运动仅考虑折痕的位置和折叠角度,不需要考虑材料厚度,通常为纸折叠.根据折叠需求可分为折痕设计、自折叠路径规划和切割折叠.
不同的折痕设计会造成不同的折叠结构,折痕形式可分为直折痕和弯曲折痕,分别适用于刚性折叠和弯曲折叠.
自折叠折纸技术是通过对折叠材料施加刺激,将自身沿着有效的折叠路径折叠成所需形状.自折叠的折叠路径是指平面沿折痕折叠成目标形状的折叠过程,有效折叠路径是指每个折痕和平面在折叠过程中是刚性且不发生碰撞的(如图3所示).自折叠寻找有效折叠路径可以看成是折叠初始位置到目标位置的路径规划问题.
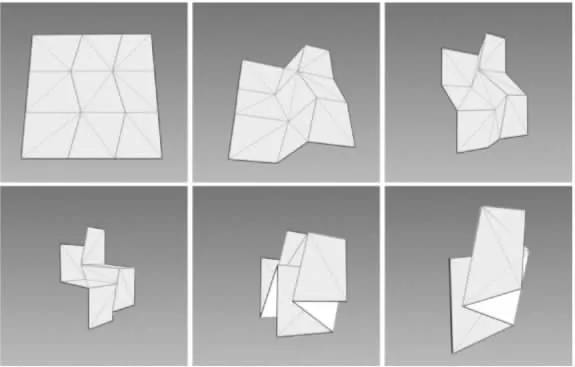
图3 Miura图案的自折叠过程[9]
切割折叠是指在折痕设计基础上结合切割的折叠方式[10],通过在平面上添加切口,利用切割产生的弹力结合折痕形成复杂的几何图形.
2.3 三维折叠
折痕图案主要为零厚度的纸张创建的,而有些折叠结构是不可以忽略厚度的,例如屋顶、太阳能电池板和太空镜.而三维折叠是指折叠对象为三维有厚度的物体,即考虑折痕之间的厚度约束及折叠面厚度的情况下进行无碰撞和自交的折叠运动.
3 几何折叠算法
本节根据折叠对象不同,从杆折叠、平面折叠、三维折叠3个方面对几何折叠算法的研究进展进行论述,总结这些算法的主要工作、算法思路及特点.
3.1 杆折叠
连杆结构的配置是指对所有连杆端点位置以及连杆方向和关节角度的指定.最早的在配置问题是1992年Hwang等[11]提出的对连杆结构进行运动规划的配置空间,重新配置决策问题简化为在配置空间中初始配置到最终配置的运动规划问题.
2008年,郭益深等[12]开发了用于控制自由浮动双臂空间机器人进行折叠运动的自适应RBF神经网络控制器.该方法的优点是不需要线性地参数化系统的动态方程,也不需要预先知道任何实际的惯性参数,适用于空间机器人的实时和在线应用.
2014年,Cai等[13]采用自然坐标法研究平面闭合双链连杆机构.利用不同约束条件来形成系统约束方程,获得雅可比矩阵计算链接的自由度.该方法可以用来寻找一些新的平面闭环连杆机构.但是,如果连杆在某些特殊配置中具有许多奇异的运动路径,则无法给出真实自由度.
2016年,Zheng等[14]提出了在3D中构造可部署剪刀连杆的方法.该方法将Hoberman的2D连杆构造算法[15]扩展到3D,使用多价连接节点,该节点具有多自由度,可增加该连杆结构的旋转方向.该算法的不足在于为了避免碰撞会局部变形钢筋的形状,且没有进行受力分析.
2018年,饶聪等[16]提出生成可展的 2 层多边形剪刀结构的方法.采用直杆和旋转节点连接多边形.计算最大张角得到折叠范围,多边形剪刀结构在此范围内运动不会碰撞,使其能够通过变形尽量压缩至一个平面.不足在于只采用 3 根直杆连接两层多边形剪刀结构时,模型处于一个不稳定的状态.
杆折叠算法重点在于解决配置空间中的运动规划问题.但是运动规划问题只针对单一自由度的连接节点,且连杆结构是开放链.而对于闭合环形或有多自由度节点的连杆结构,则更多考虑碰撞检测问题.
3.2 平面折叠
平面折叠是沿着平面上折痕图案进行折叠运动的,根据折叠需要不同,可进一步分为折痕设计、切割和自折叠路径规划3类.
3.2.1 折痕设计
纸折叠的折痕设计按其折痕形式可分为直折痕、弯曲折痕和辅助结构.
直折痕折叠是将折叠面看作刚性不可变形的连杆,折痕看作铰链的运动模型.典型的直线折痕结构有Miura-ori折痕[17]、Waterbomb折痕[18]、Yoshimura折痕[19]和对角线折痕[20].2013年,Schenk等[21]提出基于Miura-ori折痕的折叠壳结构.该结构内部单元为刚性折叠,具有负泊松比特性,但折叠壳结构可以形成扭曲曲面,泊松比为正.
弯曲折痕是指在折叠过程中折痕链接的平面会发生变形和弯曲.2008年,Martin等[22]提出了基于优化的计算框架.该框架从离散角度讨论弯曲折痕,并进行弯曲褶皱表面的几何优化.不足之处在于对于弯曲程度复杂的曲面不能很好的表示.
2017年,Martin等[23]提出了由弦驱动的弯曲折叠表面,当拉动弦网络时,会沿折痕抬起平板以形成自由形状.该折叠运动通过近似等距的变形将平面变为折叠形状,发现相应的可以被驱动以产生相同的折叠顺序的弦网络.但不是每个弯曲的折叠形状都可以用弦折叠.
2019年,Jiang等[24]通过建立与伪测地线的连接来获得可能的折痕模式,离散折痕并优化四边形网格,从而成为离散的褶皱结构.该结构享有连续的规则保持展开,平坦折叠状态以及沿着折痕的恒定折叠角.
2010年,Tachi等[25]提出折合分子的概念,将单张材料折叠成给定的多面体表面,提出基于两步映射和边缘分裂的算法,将折叠问题转换为在平面纸上布置表面多边形的问题,并通过折合分子连接多边形.但是该算法的不足在于对于无法映射的模型不适用.2017年,Erik等[26]提出的算法使用Voronoi图作为其折痕模式的基础,顶点和边沿增加了小的附加结构,然后折叠每个Voronoi单元.该算法具有水密性,折叠将纸张的边界映射到表面的指定边界内,几何特征是每个凸面都是无缝折叠的,适用于任何多面体流形.
平面折叠主要研究周期性的折叠结构用于拟合曲面,但是仅适用于双曲曲面的近似模拟;针对特征复杂模型的折叠拟合,通过添加附加结构设计折痕图案,实现了通过折叠生成三维模型的目标,但是会在原有材料的基础上增添更多的材料.
3.2.2 切割
2010年,Li等[27]人提出基于用户给定3D模型的情况下生成弹出式纸结构的算法.该算法给出了模型平面布局即分段线性曲面的几何公式,以平面布局的几何图形为基础,通过切割和折叠可以物理弹出.目前的算法着力于可实现性,但是它并不能达到一个完全令人满意的“外形”.
2013年,Sang等[28]提出通过切割和折叠单张纸以产生3D弹出窗口的原始建筑设计方法.该方法提出了新的几何条件,以确保所生成弹出窗口的可折叠性和稳定性.这些条件涵盖了广泛的弹出几何图形,使得该算法能够接近于更多的形状.
2014年,Castle等[29]开发了一套适用于切割、粘贴和折叠晶格的简单规则.该规则确定了晶格结构的基本单位.切割后留下的间隙通过“爬升”或“滑行”运动或两者的结合而闭合,以形成3D阶梯状表面.
2016年,Castle等[30]将切除以非零高斯曲率的点的形式引入到基础晶格中,将生成阶梯结构的规则减少到最低限度.该方法通过添加新材料统一了多种剪切和粘贴操作.由于沿平面分布高斯曲率的局部来源的自由度增加,因此该方法提供了更多从初始平面中创建任意形状的机会.但是,缺点是还不适用于逆向设计算法.
3.2.3 自折叠路径规划
2011年,Byoungkwon等[31]提出可编程纸张通过自折叠实现不同形状的规划和控制算法.该算法将连续折叠运动计划为所需状态,得到可行的序列,通过优化覆盖这些图案,最后确定折痕图案,以实现形状控制.
2012年,Zhong等[32]提出用于计划刚性折纸运动的随机方法,使用非线性优化方法在给定样本周围找到有效配置.考虑到对称性并重用基本折痕图案上的折叠路径,利用其对称性来降低自由度,可以确保折纸在连续折叠运动过程中的刚度,有效地折叠大折纸镶嵌.
2015年,Zhong等[33]提出了在离散域中采样的多自由度折纸的折叠路径规划,使折纸从展开状态连续进入折叠状态.该方法可以在更短的采样时间内找到更多有效的配置,同时可以快速发现隐式折叠顺序,提供了指导许多折纸的折叠过程的关键信息.
3.3 三维折叠
2014年,Zhou等[34]人提出利用连续折叠序列将三维物体转换为立方体或盒的方法.该方法将对象分割为体素,并搜索可以从输入形状折叠到目标形状的体素树.该方法可以产生一个单一的、连接的对象,物理地从一个形状制造和折叠到另一个形状.
2015年,Chen等[35]提出能够再现与零厚度折纸相同的厚板刚性折叠方法.厚板折叠运动可以看作是空间连杆结构运动,但是该结构对于非四折痕顶点折纸模式通常包含多个自由度,只能通过对称或其他方式降低模型的自由度来实现等效性.
2016年,Chen等[36]引入平面对称的Bricard连杆机构形成厚板Waterbomb结构.Bricard连杆机构在对称折叠条件下具有单一自由度,可以实现非零厚度折叠与零厚度折叠的等效运动.由于该结构在扩展状态和封装状态之间具有很大的可展开比,因此有可能用于折叠大型平面.
2016年,Jason等[37]将平面折痕转换为多面分隔的折痕,用两个平行的对称偏移一段距离折痕代替输入折痕中的每个扁平折痕.丢弃每个折痕图案顶点附近的材料以适应折痕变宽.该算法可以识别并去除折痕一侧的某些表面材料,以避免自相交.
2018年,Alden等[38]通过开发能够产生具有所需特征的空间链接排列的方法,实现厚板折叠运动.这些特征包括没有自相交、保持与铰链节点相同的自由度以及存在简单的运动学模型.铰链转置、厚度调整线和分割顶点被提议为生成具有这些特征的链接置换的方法,将有助于创建适用于连杆镶嵌的修改后的空间连杆.
4 评价分析
本节总结几何折叠的评价指标,并分析比较3类折叠算法.
4.1 评价指标
由于连杆结构是由刚性连杆和旋转关节组成,其折叠运动多依靠关节进行旋转运动,所以关节的自由度(Ndof)决定了连杆结构运动空间的维度,是杆折叠的一项重要指标.
连杆具有两种关节,固定关节和自由关节,固定关节不会增加自由关节,自由关节会增加2个Ndof,而杆如果没有多余,则会消除1个自由关节.一个连杆结构具有j个自由接头和r个杆,则该连杆结构的自由度Ndof为:
Ndof=2j-r
(1)
连杆结构的另一个评价指标为收缩比V[14],即为连杆结构在其最收缩状态下的包围体积Vs与在其最膨胀状态下的体积Ve之比:
(2)
平面折叠常用于构造三维结构,其形状的刚度可以根据表面的稳定性来衡量.通常,该结构的不稳定性数[25]由下式给出:
DegreesofInstability=3v-e-6
=e0-3
(3)
其中v,e和e0分别是三角化曲面的边界上的顶点,边缘和边缘的数量.
已知刚性折叠的每个折叠面是平坦不变形的,而弯曲折叠的折叠面会发生形变,所以折叠面的刚度由其平面度ωplanar度量[24],计算公式为:
(4)
其中dmax是平面中对角线的距离,dav是对角线的平均长度.
折叠结构的可展开性由顶点角度缺陷ωangle来衡量[24],计算公式为:
ωangle=2π-θsum
(5)
其中θsum为该顶点一环领域的夹角角度和.
由于折叠成的三维结构与原模型存在拟合误差,可用折叠模型Mo与原模型M之间的Hausdorff距离[39]来表示,其计算公式为:
H=|h(Mo,M)|
(6)
其中h(Mo,M)表示Mo到M的Hausdorff距离.
4.2 算法分析与比较
本节根据上述总结的典型算法思路4.1节的评价指标,分类对几何折叠算法进行分析与比较.
4.2.1 杆折叠
表1展示了关于杆折叠算法的分析比较,主要比较因素包括节点自由度、运动空间维度、算法复杂性和贡献.

表1 杆折叠算法研究成果分析
在杆折叠的算法中,文献[12,13]提出连杆结构的几何约束,通过求解约束条件和碰撞检测得到运动路径,但是其运动为平面内运动;为了使连杆应用在3维空间中,文献[16]采用的方法是分层连接,但是本质上连杆结构还是平面运动;文献[14]则是通过添加多价节点的方式提高自由度实现连杆结构在三维空间的运动.
4.2.2 平面折叠
平面折叠算法的分析与比较如表2所示,主要比较因素包括分类、折痕形式、折叠方式、评价指标和贡献.

表2 平面折叠算法对比
在折痕设计中,直折痕和弯曲折痕因具有周期性和对称性,仅适用于双曲面和特征较少的曲面的折叠模拟;对于复杂三维模型的模拟,文献[25]采用在映射图中添加折合分子的方式折叠,该方法依赖模型切割,折叠后不能完全闭合;在此基础上,文献[26]提出水密性折叠,优化折合分子的大小和位置,使模型的每个凸面都是无缝的.在切割折叠算法中,文献[27]提出的基于分段线性曲面平面布局的弹出式纸结构给出的几何条件只满足一类模型,对于特征复杂的模型并不能完全保留其外形特征,而文献[28]采用更一般的几何条件,可以适用于更多的模型,并且使用图像域方法进行平面布局,在保留轮廓特征、缩小体积、制作时间方面明显优于文献[27].
4.2.3 三维折叠
三维折叠算法的分析与比较如表3所示,主要比较因素包括折叠方式、自由度和贡献.

表3 三维折叠算法对比
在三维折叠算法中,文献[34]主要研究实心三维模型的折叠运动,实现两种模型形状之间的转换,应用与可重构机器人领域中,但是在模拟精度上存在不足,存在菱角;而文献[35-38]重点在于实现有厚度折叠与零厚度折叠的等效运动,不关注模型的模拟,主要应用于工业设计.
5 应用领域
本文从生物医疗、工业设计和机器人设计领域这3个方面出发,介绍几何折叠的应用情况.
5.1 生物医疗领域
在生物医疗领域中,几何折叠结构因其具有伸缩和扩张的特性,可以通过特定方式进行变形而被广泛应用于医疗支架,药物运输[40]、生物医学传感器[41]等用途.
2006年,Kuribayashi等[42]提出折叠支架设计,该支架通过添加折痕图案实现圆柱形管状折叠,应用于微创手术,用于打开和保护阻塞管道.2007年,Christina等[43]使用可液化铰链对二维模板进行光刻图案化,根据其加热后自发折叠的特性构造药物运输容器.该容器具有有限的封装体积,可以制造得足够小以穿过皮下注射针头.2012年,Rohan等[44]讨论了全聚合容器的自折叠和自折叠聚合物在药物输送中的应用.自折叠可以在组装过程中封装或自动装载治疗用货物,对于药物输送应用很重要.以后的发展挑战在于如何将自折叠聚合物容器进一步小型化至亚微米规模.
2014年,Kise等[45]评估新型弯曲支架在扩张阻塞血管中的应用.该弯曲支架基于连杆结构并由Goku曲线连接.尽管支架以弯曲的方式扩张,但支架组件在其弯曲部分扩张期间也一致旋转,使其在较小和较大的曲率上产生均匀的应力,可以更好更安全的应用在急性弯曲病变中.
2017年,Lin等[46]提出基于折叠的Miura结构的光电探测器阵列组成柔性电子设备,为柔性设备提供出色的全向光收集功能,并具有出色的可变形性,应用于可穿戴设备、生物医学传感器、家庭医疗、电子皮肤等.
5.2 工业设计领域
在工业设计领域中,工业产品结合几何折叠技术可产生高度变形[47]、缩小存储空间[48]、提升原有功能[49]等特点.
2012年,Martinez等[50]基于弹性体嵌入片状结构、及复合纤维结构材料,实现了基于折叠的多用途柔性气动驱动器,提高了弹性体驱动器的刚度.该结构可举起自重120倍的负载,同时结合其他组件可以增加功能.
2013年,Song等[51]提出折纸锂离子电池,可以高度变形.折纸电池是通过Miura折痕图案折叠而制成的.所得的折纸电池具有明显的线性和面形变形性、大的可扭曲性和可弯曲性.
2018年,Zhu等[52]提出了折纸启发的可折叠多显示智能手表,通过多个手腕式显示器的可折叠结构达到与智能手表的交互.该研究为可折叠可穿戴设备的未来面向产品的工作提出了重要而必要的步骤.
2020年,Tao等[53]提出并设计高性能的剪刀结构变形折叠机制,该机制利用了简单的非相交的有角度元素和类似剪刀的直形元素,具有单自由度、快速致动能力和大变形比的优点,用于可控的可扩展多轴飞行器系统.该机构具有快速适应复杂且动态变化的出色能力.
5.3 机器人领域
几何折叠技术因其在易于制造、折叠式结构紧凑、尺寸可伸缩、保持几何形状和传递力方面[54]具有优势而被广泛应用在机器人领域内.
2017年,Miyashita等[55]基于自折叠的外骨架变形,扩展提高了机器人的功能和性能. 2017年,Li等[56]基于流体驱动折叠实现了人工肌肉的折叠架构,该人工肌肉系统的骨架采用弹簧折纸状的折叠结构.2019年,Li等[57]提出半球形空心的真空驱动软抓取器的新设计.该软抓取器基于折叠展开的骨架结构、密封皮肤和连接器等构件,可抓取物体的形状不受限制.
2020年,Hauser等[58]介绍自重构模块化机器人.该机器人通过模块化技术将具有编程能力的立方块组合在一起,实现体折叠运动过程,共同完成一系列复杂的任务.
2020年,Sahand等[59]使用具有定制的非线性刚度的机器人跳跃机制来改善机器人的动态性能.使用Tachi-Miura多面体波纹管折纸作为具有嵌入式能量存储的跳跃机器人骨架,使其比线性弹簧能存储更多的能量,改善了机器人的跳跃高度和飞行时间.
6 总结与展望
本文对近年来几何折叠算法进行整理分析,并根据折叠对象和需求将几何折叠分类,提出折叠的评价指标,总结和比较每一类折叠的相关研究工作和算法思想,并介绍几何折叠的相关应用.
目前几何折叠技术对准确性和时效性的要求越来越高,需要提供更为精准和高效的折叠算法.本文基于对现有的算法进行分析,提出了几何折叠算法的两个发展方向,分别为提高算法效率精度和自驱动.
1)提高算法效率精度
在几何折叠算法中,分为两种折叠目标,寻找有效折叠路径和曲面逼近.现有的寻找有效折叠路径算法采用自适应神经网络控制器来进行折叠路径规划和碰撞检测.结合神经网络寻找有效的折叠路径,高效且精准.例如使用束搜索和模拟退火算法寻找有效折叠序列[58],通过神经网络训练多面体的线性无碰撞折叠路径[60].本文认为,通过使用更为高效的神经网络和搜索算法,可以提高寻找有效折叠路径的效率,节约成本.通过几何折叠来逼近曲面是折叠的另一种应用,在固定材料的情况下目前大多数算法不适用于特征复杂的三维模型.未来的研究方向需要将模型的复杂特征与折痕图案结合考虑,实现更多模型的形状逼近,并提高其逼近精度.
2)自驱动
大多数折叠需要外力驱动才能开始运动,但有些应用中施加外力是不切实际的.自驱动技术则是在不需要外力情况下,通过化学或物理等特性驱动折叠运动,例如通过光刻图案化[17].本文认为,自驱动利用活性材料来发挥折叠运动是未来的重要研究方向,主演研究重点在于找到适用于具体应用的特定材料和有效折叠路径,并根据实际提供驱动条件,该技术在未来有待进一步研究探索.

