基于簇内样本平均分类错误率的混合采样算法
熊炫睿,陈高升,熊 炼,张 媛,程占伟,付明凯
1(重庆邮电大学 通信与信息工程学院,重庆 400065)
2(重庆工程学院,重庆 400056)
1 引 言
分类学习是机器学习的重要研究方向之一,许多实际应用中存在类别分布不平衡的数据,即数据集中不同类别的样本数量相差很大的情况,例如入侵检测、医疗检测、信用卡欺诈等应用场景,少数类样本在这些应用场景中也很重要[1,2].机器学习模型在对类别分布不平衡的数据进行分类时,对少数类的召回率会较低.
现有算法层面的方法和数据层面的方法[3]能提高分类模型对类别不平衡数据的分类效果.算法层面的方法包括代价敏感学习方法和集成学习等方法.数据层面的方法有欠采样方法、过采样方法与混合采样方法.欠采样方法通过减少多数类样本使数据达到平衡,例如各种基于聚类的欠采样算法以及随机欠采样算法.过采样方法通过增加少数类样本使数据达到平衡,例如SMOTE算法.混合采样方法将过采样方法与欠采样方法相结合,通过对少数类样本采用过采样方法提高数据量,对多数类样本采用欠采样方法降低数据量,将不平衡数据转化为平衡数据集.
近年来,许多学者对SMOTE算法进行了改进优化.燕昺昊等人通过改进的SMOTE算法增加少数类样本数量,用得到的平衡数据集训练一个深度循环神经网络分类器,对少数类的召回率显著地得到提高[4].陈虹等人提出一种改进的SMOTE算法—基于最大相异系数密度的SMOTE算法,对少数类样本采用该算法进行过采样,然后用得到的平衡数据集训练梯度提升决策树分类器,对少数类的召回率显著地得到提高[5].然而,在处理不平衡的数据分类时仅采用SMOTE过采样算法,会引入过多的噪声,从而影响分类器的准确性.
此外,有不少学者对基于聚类的欠采样算法进行了相关研究.Ng等人提出了一种基于聚类的欠采样算法—DSUS(Diversified Sensitivity Undersampling)算法,该算法首先对多数类样本集采用聚类算法,然后根据各个簇的代表点的敏感度大小选择多数类样本[6].魏力等人对多数类采用K-means聚类算法,簇中心点根据NearMiss距离进行排序,按序在各个簇内提取若干个与簇中心点相距最近的样本,从而减少多数类的样本数量,将不平衡数据转化为平衡数据集[7].徐丽丽等人采用聚类算法将多数类样本聚类,从每个簇中根据采样率选取与簇中心相距最近的若干个样本,构成平衡样本集[8].Di等人提出了一种快速搜索与发现密度峰值的自适应聚类算法,对多数类采用该算法进行聚类,然后按照一定比例对每个簇进行欠采样[9].然而,以上这些基于聚类的欠采样算法对多数类样本采用聚类算法后从簇中选取样本,没有考虑根据簇内样本总体信息对簇进行筛选,事实上对于构建分类器而言有些簇价值很低,因此从这些簇内提取的多数类样本代表性不够,例如:在支持向量机(Support Vector Machine,SVM)算法中,与分类边界相距很远的簇的内部样本不会是的支持向量,这些簇对构建支持向量机分类器没有价值.此外,以上这些基于聚类的单纯的欠采样算法会丢弃过多的多数类数据,从而导致过多的多数类信息被丢失.
近年来,许多学者对混合采样方法进行了相关研究.Han等人提出了GSRA(Gaussian mixture model based combined resampling algorithm)算法[10],GSRA算法对少数类采用SMOTE方法增加样本数量,此外,该算法对多数类采用高斯混合聚类算法,从各个簇内中选取部分样本,从而减少多数类样本数量.张艳等人对多数类采用一种基于加权重叠距离的k-modes聚类算法,并选取簇中心,以减少多数类样本数量;同时,对少数类采用SMOTE算法增加样本数量[11].然而,上述两种混合采样方法中对多数类采样的基于聚类的欠采样方法,没有考虑到对于构建分类器而言有些簇价值很低,而从这些簇内提取的多数类样本代表性也就不够.
针对上述问题,本文提出了一种基于簇内样本平均分类错误率的混合采样算法(SABER).该算法定义了“簇内样本平均分类错误率”V(C)的概念,V(C)包含簇内所有样本的总体分类信息,该混合采样算法首先对少数类使用SMOTE方法增加样本数量,接着选取各类别的部分数据添加至平衡样本集中,并用该样本集训练一个初始的分类器,然后进行多轮迭代,在每一轮迭代中执行:采用K-means聚类算法对多数类样本集中剩余的还未用于训练分类器的样本进行聚类,然后计算出各个簇的V(C),筛选出V(C)最大的若干个簇,并将这些簇各自的代表点不放回地取出并添加至平衡数据集中,同时不放回地随机取出若干个少数类样本添加至平衡样本集中,使平衡样本集中的少数类与多数类数据数量基本相同的,然后在平衡样本集上重新训练分类器.重复执行以上操作,直到达到迭代次数.最终SABER算法得到一个平衡的数据集以及用该数据集训练好的分类器.
2 相关理论
2.1 K-menas
K-means算法属于无监督的聚类算法,K-means算法通过多次迭代将样本划分到不同的簇中.最小化平方误差E:
(1)
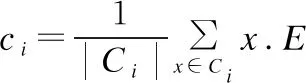
Input:样本集D与聚类簇个数r
Output:r个簇
步骤1.从样本集D中任选r个样本作为初始的簇中心;
步骤2.循环步骤3和步骤4直到簇中心不再更新;
步骤3.计算r个簇中心与样本集D中的每个样本的距离,将样本划分到相距最近的簇内;
步骤4.更新r个簇中心;
2.2 SMOTE
Chawla等人提出了SMOTE算法[12].该算法根据已有的样本合成人工样本,从而增加少数类样本数量.SMOTE算法步骤为:
步骤1.对于每一个少数类样本Si,找出样本Si的r个近邻;
步骤2.根据采样的倍率,从r个近邻中随机选出若干个样本,假设选择的近邻为Sj;
步骤3.对于每一个选出的近邻Sj,根据式(2)在Si和Sj之间随机合成一个新的样本Sn
Sn=Si+w(Sj-Si)
(2)
式中,w为一个介于0和1之间的随机数.
3 提出的SABER算法
3.1 基于簇内样本平均分类错误率的欠采样
定义1.(簇的代表点)与簇中心相距最近的该簇的内部样本称为簇的代表点.
定义2.(簇内样本平均分类错误率)给定一个分类器h和已知样本标签的簇C,簇C内样本的平均分类错误率V(C)定义为:
(3)
式中,xj为簇C内样本j,yj为样本j的真实标签,h(xj)返回分类器h对样本j的预测类别,I为指示函数,若输入为真,则返回1,否则返回0.
V(C)包含了簇内所有样本的分类总体信息,当V(C)较大,表明分类器h缺少这个簇足够的信息,因此,该簇对提升分类器性能具有较大的价值,而该簇的代表点能够提供该簇大量的有用信息,分类器可以通过对该簇的代表点的学习,从而提高分类器的性能.反之,当V(C)较小,表明分类器已经学习到该簇足够的信息了,因此,该簇无法为提升分类器提供较多的有用信息.因此,在采用基于聚类的欠采样方法减少多数类样本时,应该优先从簇内样本平均分类错误率V(C)更大的簇内选取簇的代表点,从而在减少多数类数据的同时,能选出更具有代表性的多数类数据.
本文对多数类样本集使用基于簇内样本平均分类错误率的欠采样,以降低多数类样本的同时保留尽量多的对构建分类器有用的信息.其核心思想为:首先选取各类别的部分数据添加至平衡样本集中,并用该样本集训练一个初始的分类器,然后进行多轮迭代,在每一轮迭代中执行:采用K-means聚类算法对多数类样本集中剩余的还未用于训练分类器的样本进行聚类,然后计算出各个簇的V(C),筛选出V(C)最大的若干个簇,并将这些簇各自的代表点不放回地取出并添加至平衡数据集中,同时不放回地随机取出若干个少数类样本添加至平衡样本集中,使平衡样本集中的少数类与多数类数据数量基本相同的,然后在平衡样本集上重新训练分类器.重复执行上述操作以进行下一轮迭代,直到达到迭代次数.最终SABER算法得到一个平衡的数据集以及用该数据集训练好的分类器.
3.2 SABER算法
在基于簇内样本平均分类错误率的欠采样的基础上,将其与SMOTE过采样结合,提出了SABER混合采样算法,该算法由两部分构成:1)使用SMOTE对少数类样本过采样;2)使用K-means对多数类样本聚类,根据簇内样本平均分类错误率V(C)对多数类样本进行欠采样.
SABER算法步骤如下所述,其核心思想:基于簇内样本平均分类错误率的欠采样,在下面的步骤4中.
输入:一个包含N类的不平衡的数据集、平衡采样样本数m、分类器算法h、迭代次数T、SMOTE的参数近邻数量k.
将各类别的样本划分开,共有N个样本集S1~SN,下标为类编号.输入的平衡采样数m与输出的平衡数据集Q中的各个类别的样本数近似相等,建议将平衡采样数m设置为输入的不平衡数据集中各个类别的样本数的中位数;本文中的多数类是指样本数量大于m的类,少数类是指样本数量小于m的类,非多数类包括少数类和样本数量等于m的类;多数类欠采样后的样本数量等于m,少数类过采样后的样本数量约等于m.分类器算法h采用最终将要使用的分类器算法,原因是:公式(3)说明V(C)与分类器h的分类结果相关,而SABER算法根据V(C)对多数类进行欠采样,因此SABER算法是针对分类器h进行的采样.
步骤1.对每个少数类样本集使用SMOTE进行过采样,根据式(4)设置少数类i的过采样倍率∂i,
∂i=(⎣m/|Si|-1」)×100%
(4)
使少数类样本数尽量接近平衡采样数m;
步骤2.分别对每个类的样本集使用K-means聚类算法,每个类划分为z个簇,
z=「m/T⎤
(5)
从每个簇中不放回地提取出簇的代表点,共提取N×z个样本,将其作为初始的平衡样本集Q;
步骤3.使用初始的平衡样本集Q训练一个初始的分类器h;
针对每一次迭代,t=1,2,…,T-1,重复步骤4)-步骤 6);
步骤4.对多数类样本使用基于簇内样本平均分类错误率的欠采样.分别对每个多数类剩余的还未用于训练分类器的样本数据集使用K-means进行聚类,各类生成m个簇.对每一个多数类执行如下操作:根据式(3)计算分类器h对该类的每个簇的V(C),根据V(C)由大到小的顺序对该类的m个簇进行排序,筛选出前z个簇,并不放回地提取出这些簇各自的代表点添加至平衡样本集Q中,并从该类的样本集中去掉已被提取的样本;
步骤5.从每个非多数类剩余的样本数据集中不放回地随机提取z个样本,并添加至平衡样本集Q中;
步骤6.此时平衡样本集Q中各类别的样本数量基本相同,用平衡样本集Q重新训练分类器h;重新执行步骤4-步骤6,以进入下一轮迭代,t=t+1,直到t=T-1.
输出:平衡样本集Q、已经用Q训练过的分类器h.
每次迭代中,从每个类中提取z个样本添加至平衡样本集Q中,在最后几次迭代中,z的值可能会变小,具体地设置见表1,以保证最终对各类重采样的数量达到预期的数量,即最终平衡样本集Q中多数类样本数量要等于m,少数类样本集数量为上述步骤1中以某一倍率使用SMOTE进行过采样的数量.将创建初始的平衡样本集的一次迭代包含在内,经过共T次迭代,得到一个各类样本数量接近的平衡样本集Q,同时得到一个使用Q训练好的分类器h.

表1 SABER算法流程
表1为SABER算法的流程,该算法的核心思想:基于簇内样本平均分类错误率的欠采样,在Step 4中.
4 实验与分析
本节中,我们评估了本文提出的SABER算法,所有实验均在Windows10操作系统上进行,并且使用python 3.7.3版本.
4.1 评价方法
本文将G-mean和召回率作为评价指标[13],通过混淆矩阵可以计算得出这两个指标.表2为混淆矩阵,其中Nij表示类别为Ci的样本被识别为类别Cj的个数,参数k表示类别的总数.
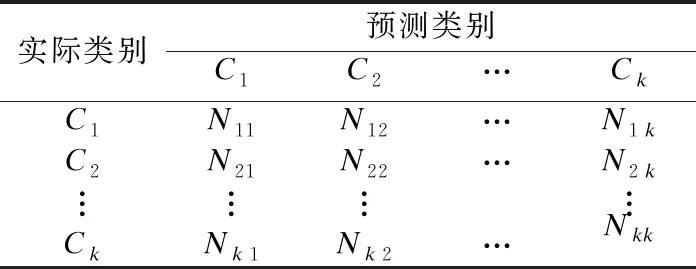
表2 混淆矩阵
类别Ci的召回率Ri为实际为类别Ci的所有样本中被正确预测为类别Ci的样本的比例,其定义为:
(6)
G-mean与各类别的召回率相关,体现了分类器的总体性能,其定义为:
(7)
4.2 实验数据与预处理
4.2.1 实验数据
在网络攻击中,各种攻击发生的频率各不相同,甚至相差很大,因此网络入侵检测是一种典型的类别不平衡的领域.KDD Cup99数据集来源于美国国防高级研究计划局公开的TCPdump数据,是网络入侵检测领域的公开的常用的数据集.该数据集提供了名为KDD Cup99_10%的数据集,该数据集如表3所示,本实验将使用该数据集验证SABER算法的有效性.

表3 KDD Cup99_10%数据集
KDD Cup99_10%包含5种类别:Normal和4种攻击:Dos、Probe、U2R和R2L,每个样本具有41个特征,表3为数据集的最大不平衡度和样本数量,最大不平衡度定义为数据数量最多的类与数据数量最少的类的数据数量比值,体现了数据集的不平衡程度,KDD Cup99_10%数据集中的样本数量最少的类是U2R,样本数量最多的类是Dos,从表3中可知,该数据集的最大不平衡度很大.该数据集中的类Dos和Normal的数量远大于类U2R、Probe和R2L的样本数量,因此,将R2L和U2R视为少数类,将U2R 、Probe和R2L视为非多数类,将Normal和Dos视为多数类.
4.2.2 实验数据预处理
1)符号型特征数值化
将数据集中的符号型特征转化为数值型特征,如service,protocol和flag等.
2)Z-score标准化
为了加快算法的收敛速度以及消除不同的特征的不同的量纲对分类结果的影响,需要对数据采取Z-score标准化预处理,计算公式为:
(8)
式中,x为原始输入数据,γ为归一化后的输出数据,μ和为原始数据集各维的均值,σ为原始数据集各维的标准差.
4.3 实验参数设置
SABER算法的平衡采样数m应该设置在训练集中的最大类样本数和最小类样本数之间,Probe类的训练样本数为这5类训练样本数的中位数,因此,将平衡采样数m设置为Probe类的训练样本数.分类器算法h应采用最终将要使用的分类器算法,在实验中,我们将常用的BP神经网络和决策树作为最终将要使用的分类器算法.完整的参数设置如表4所示.

表4 SABER算法的参数设置
4.4 对比算法
与该采样算法进行对比的其它采样算法有:
DS-SMOTE[14]:该算法是一种过采样算法,对SMOTE进行了改进,少数类中邻域密度小于阈值的样本被视为稀疏对象,在稀疏对象与其近邻样本之间合成新的样本.
DSUS[6]:该算法是一种基于聚类的欠采样算法,采用聚类算法将多数类样本集划分为若干个簇,根据各个簇的敏感度大小选择多数类样本.
GSRA[10]:该算法是一种结合欠采样与过采样的混合采样算法.首先,该算法对多数类采用基于聚类的欠采样方法—高斯混合聚类方法,将多数类划分为多个簇,然后从每个簇内提取出部分样本,从而减少多数类样本的数量;该算法对少数类采用SMOTE方法,以增加少数类样本数量.
4.5 实验结果与分析
因为在许多相关研究中将BP神经网络和决策树作为分类器算法,所以本实验选择将BP神经网络和决策树作为分类器算法,DS-SMOTE、DSUS和GSRA采样算法得到的数据集分别用来训练这两种分类器.
由表5可知,本文提出的SABER算法和过采算法DS-SMOTE、欠采样算法DSUS以及混合采样算法GSRA相比,SABER算法上的G-mean值最高,可知SABER算法的总体分类性能是最好的.由表6可知,SABER算法和其它采样算法相比,SABER算法上的少数类Probe、U2R和R2L的召回率是最高的,同时有较高的多数类召回率.究其原因,SABER算法作为一种混合采样算法,与单纯的过采样DS-SMOTE算法相比,SABER算法生成的少数类新样本更少,因此模型学习到的噪声更少;与单纯的欠采样DSUS算法相比,SABER算法丢弃的多数类样本更少,机器学习模型能够学习到更多的多数类样本信息.SABER混合采样算法与GSRA混合采样算法对少数类都采用SMOTE方法,以增加少数类的样本数量,这两种混合算法之间的区别在于采用不同的欠采样方法减少多数类样本数量.GSRA混合采样算法对多数类采用基于聚类的欠采样方法,从所有簇内提取若干个样本,没有考虑到有些簇对提升分类器性能而言价值很低,从这些簇中提取的多数类样本代表性也就不够.而SABER混合采样算法在对多数类进行聚类后,根据簇内样本平均分类错误率V(C)筛选出对提升分类器性能更有价值的簇,并选取这些簇各自的代表点.因此,与GSRA算法相比,SABER算法能够选取更具有代表性的多数类样本,分类器能从这些样本中学习到更多的有效的多数类信息,因此其分类性能更好.
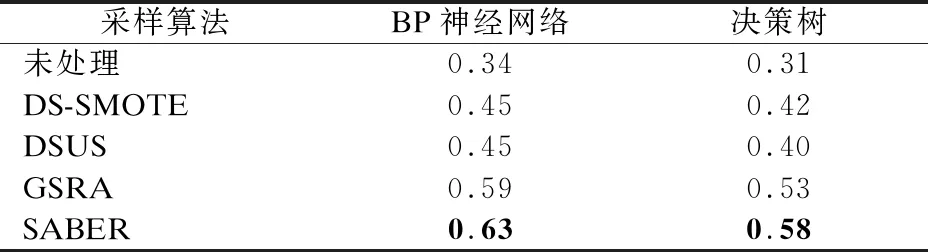
表5 SABER算法和其它采样算法上的G-mean值比较

表6 SABER算法和其它采样算法上的各类的召回率比较
5 结 语
针对类别不平衡的问题,本文提出了一种基于簇内样本平均分类错误率的混合采样算法—SABER算法,该算法对多数类样本进行聚类后,根据簇内样本平均分类错误率筛选出对提升分类器性能更有价值的簇,并选取这些簇各自的代表点,从而选出具有代表性的多数类样本;SABER算法采用SMOTE算法增加少数类样本的数量;最终得到一个平衡的数据集.实验结果表明,在对类别不平衡的数据进行分类的场景中,与其它采样算法相比,SABER混合采样算法具有更好的整体分类性能以及更好的少数类样本分类性能.

