动态数据下的三支区间离散模型

章耀坤,于 洪,胡 峰

(重庆邮电大学 计算智能重庆市重点实验室,重庆 400065)

1 引 言

数据预处理是指在进行数据分析之前对原始数据进行的一系列处理,使得原始数据结构与数据分析算法相互适配,从而获得更加准确的分析结果.例如,工业中的大数据普遍存在数据维度高、数据类型复杂等问题,进而导致现有的经典数据挖掘算法对此类数据无法进行有效分析[1].因此,数据预处理对于数据分析结果很重要.针对数据高维度问题,目前已取得一定的研究成果[2,3].另一方面数据类型复杂问题仍需进一步研究.

离散化是数据预处理中针对数值属性数据的预处理方法.大数据中利用属性或特征用于描述应用程序中数据元素的字符.常见的属性有数值属性和标称属性.由于数值属性值是一组连续的数值,例如温度、长度,经典数据挖掘算法无法直接处理数值属性数据.因此,我们需要在数值计算的背景下将连续的数值数据简化为离散的标称数据.

对于数据离散化的研究,研究者们在这方面取得了一系列的研究成果.例如,Wong和Chiu[4]于1987年提出了经典的等宽离散和等频离散.1991年Chiu等[5]提出了基于最大熵的离散方案.该算法将信息熵引入离散算法中,用于自动确定的离散过程中的区间数.Rahman和Asadi[6]提出了一种新的离散方法,其中通过低频区间合并策略,在保障离散效果不变的情况下,减少区间数量.Hacibeyoglu和Ibrahim[7]在2018年提出了一种无监督的离散模型EF_Unique,通过区间中心点获取区间切点.

另一方面,数值属性数据的离散过程是一个充满不确定性的过程.粗糙集理论[8,9]是处理不准确,不一致和不完整信息的有效工具.目前基于粗糙集的离散研究已取得一系列研究成果.Jiang和Sui[10]提出了一种有监督多目标离散算法SMDNS.该算法在SMD[11]算法的基础上,引入参数μ实现了对区间宽度进行限制.2018年,Grzymala-Busse和Mroczek[12]成功地将粗糙集理论与信息熵理论相结合,该算法通过条件熵确定区间切点,并使用上下近似集提出了新的一致性等级评估从而确定区间数目.2020年Sun等[13]基于粗糙集理论提出一种有监督离散算法,该算法主要思想是生成尽可能多的纯区间,实现对纯区间的合并以减少区间数.

尽管目前有许多离散算法获得较好的效果,但是其中大多数离散算法仅作用于静态数据.传统动态离散算法关注于学习器与离散过程的同时进行,例如Au等[14]提出了一种基于模糊集(ITFP)的动态离散方法.而针对动态的增量式数据的离散算法研究较少.然而动态或增量是大数据的典型特征.如图1所示,图1由SMDNS对表1中数值属性b离散后的区间样例图.在数据动态变化中,由于原始数据中存在的局限性,导致在离散过程中生成的区间之间存在间隙.如果间隙太大,则不能很好地对间隙中的值进行离散处理.因此,根据增量数据的特性,离散区间之间的间隙变化变得尤为重要.

表1 离散样例表

图1 传统区间样例

这里如果不确定的空白区间不能很好地表示,离散过程中则不能真实地反映区间范围.在Yao[15，16]的三支决策理论的启发下,本文提出了一种基于三支决策的自适应动态区间离散化方法TDD.近年来,三支决策已在许多领域中使用.例如,Yu[17]提出了三支聚类分析的框架,并提出了一系列三支聚类算法[18，19]；为了解决自动编码器网络中的长时间训练问题；Zhang等[20]提出一种顺序三支决策模型；Herbert和Yao[21]将博弈论与三支决策相结合以获取合理的阈值对.

因此,为了解决动态数据离散过程中区间切点的不确定性问题,本文结合了基于粗糙集理论的离散化方法在可解释性方面的优势,以及三支决策善于处理不确定性的特点进行了研究.本文主要贡献概述如下：

1)提出了一种针对增量数据离散的框架模型TDD,以解决增量大数据离散区间融合的问题；

2)三支区间表示用于反映属性值和间隔之间的关系,即：核区间、边缘区间和其他区间；

3)根据实际情况,本文中对空白区间进行了客观表述与定义.并通过实验讨论了空白空间分配问题；

4)本文采用新旧区间融合迭代方案来解决区间更新问题.通过静态离散算法处理新的样本集以获得新的区间集.将新区间集和旧区间集进行融合迭代以处理动态数据,从而节约了时间代价.

2 预备知识

2.1 信息系统与离散区间

定义1[9].一个信息系统S可以表示为S=(U,A,V,f),其中U表示论域；A=AT∪AD是属性全集,子集AT和子集AD分别称为条件属性集和决策属性集；V=∪r∈AVr是属性值的集合,Vr表示属性r∈A的属性值范围,即属性r的值域；f:U×A→V是一个信息函数,它指定U中的每一个对象x属性值.

定义2[22].传统区间可以表示为：

Da={[pmin,p1),[p1,p2),…,[pn,pmax]}

(1)

其中Da表示数值属性a的离散区间集,pmin、pmax分别表示最小切点值和最大切点值；n+1表示Da区间集中区间总个数.

2.2 问题定义

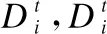
3 基于三支决策的动态数据区间离散方法

本章节将对本文提出的TDD模型进行详细的讲解.在整个模型中可以分为两个部分,即对静态数据的离散处理与对动态数据的离散处理,如图2所示.

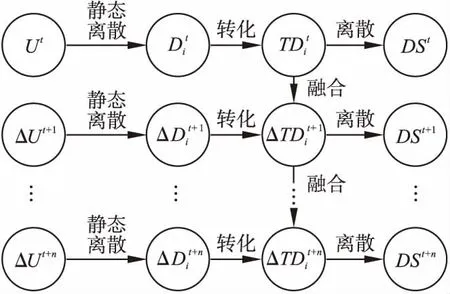
图2 动态数据区间离散方法TDD

静态离散处理部分,本文选择具有可解释性的SMDNS[8]算法.SMDNS算法的核心公式是公式(2)和公式(3).公式(2)通过粗糙集正域概念,通过判断相邻对象集合并之后对对象集的识别是否矛盾，在无矛盾的情况下对两个对象集进行合并.公式(3)实现了对区间宽度的控制.

(2)

(3)

对于动态处理,TDD采取新旧区间集的融合策略.首先TDD通过对新数据静态离散处理获得新区间集.然后将新离散区间集与旧离散区间集融合以获得全新的离散区间.可见,本文工作主要难点在于动态数据离散过程中区间集的融合.本节将从4个方面解决此问题:1)通过引入三支决策,将传统离散区间重新定义为三支区间;2)以三支区间为基础对SMDNS算法进行改进,从而获取三支区间集;3)定义空白区间来描述不确定区间;4)提出了区间融合算法,实现了新旧区间的融合.

3.1 三支区间

定义3.三支区间可以表示为：

TDa={[pmin,p1,1,p1,2,p1,3),[p1,3,p2,1,p2,2,p2,3),…,[pn-1,3,pn,1,pn,2,pmax]}

(4)

其中TDa表示数值属性a的离散区间集,pmin、pmax分别表示最小切点值和最大切点值,n表示TDa区间集中区间总个数.在定义3中[pi-1,3,pi,1,pi,2,pi,3)来表示区间di,其中pi,1和pi,2是根据数据驱动得到的区间di的核切点,核切点点是真实存在的样本数值数据.pi-1,3和pi,3是区间di的边切点,边切点是根据区间di的内切点即pi,1和pi,2与其相邻区间的内切点即pi+1,1和pi-1,2通过计算来获得.

利用三支区间表示区间,可以清晰的将区间确定范围和不确定范围进行区分.在区间融合算法中,只针对确定的区间范围进行融合,对不确定的区间范围进行延迟处理.使得融合后的区间即保证确定性,又保障了对区间不确定范围的有效识别与控制.

定义4.核区间集可以表示为：

CDa={[p1,1,p1,2],[p2,1,p2,2],…,[pn,1,pn,2]}

(5)

定义5.边缘区间可以表示为：

EDa={[pmin,p1,3),[p1,3,p2,3),…,[pn-1,3,pmax]}

(6)

定义6.空白区间可以表示为：

BDa={(p1,2,p2,1),(p2,2,p3,1),…,(pn-1,2,pn,1)}

(7)

如图3所示,分别表示经过离散处理后的核区间集、边缘区间集、三支区间集.核区间是通过静态离散获取的确定的区间范围；空白区间表示其相邻两个核区间不确定的边界范围；边缘区间是包含核区间,在传统的静态离散算法中,边缘切点是通过相邻核区间切点求均值获得.通过三支区间表示,能过合理的将区间分布进行表示,在融合过程中可以针对核区间与空白区间采取不同的措施进行处理.

图3 三支区间离散样例

3.2 TDD模型

算法1.基于三支决策的动态数据区间离散方法(TDD)

输入：t时刻,信息系统St=(Ut,A,V,f)；实验参数μ；t+1时刻,信息系统St+1=(Ut+1,A,Vt+1,ft+1)；

输出：离散后的信息系统DSt+1．三支区间集TDt+1；

1.TDt←St；/*初始化TDt+1,本文选取SMDNS算法进行静态离散*/

2. IfSt+1exist do

3.ΔTDt+1←ΔSt+1=(ΔUt+1,A,V,f)；

/*ΔUt+1=Ut+1-Ut*/

4. Forito |NA|/*|NA|表示数值数据个数*/

5.TDt+1←fusion(ΔTDt+1,TDt)；

6. End for

7. ReturnDSt+1←Updata(St+1,TDt+1),TDt+1；

TDD算法根据空白区间和核区间之间的互补,实现离散过程中区间宽度的动态自适应过程.算法1中,我们详细描述了TDD算法.通过算法1,TDD实现了对静态区间集的融合.区间融合算法将在3.3节详细讲解.算法1首先利用SMDNS算法获取三支区间集.SMDNS算法时间复杂为O(|NA|2×|U|log2|U|),其中|NA|表示属性A中数值属性个数.空间复杂度为O(|U|+max(|Va∈NA|)),其中max(|Va∈NA|)表示数值属性NA中属性值个数最多的值.再对三支区间进行融合,实现动态离散三方.算法1的总时间复杂为O(|NA|2×|U|log2|U|+|NA|).算法1的空间复杂为O(|U|+max(|Va∈NA|)+|NA|×max(|TDa∈NA|),其中max(|TDa∈NA|)表示为三支区间集中区间数的最大值.

3.3 区间融合算法

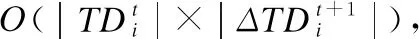
(8)

其中i代表行数,j代表列数,oij代表第i行、第j列对应的数值,即第i个区间在第j类中的样本数量.ni代表第i个区间中样本总数,cj代表第j类样本总数,N代表全部的样本总数.

本文假设相邻或相交的两个区间存在潜在一致性关系.TDD中通过公式(8)判断区间之间一致性,从而实现区间融合或者分裂.为保证融合后区间单调性,自由度值的选择应该随数据的情况而定.

算法2．区间融合算法

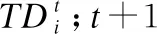
输出：融合后三支区间集TDt+1；

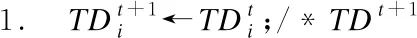
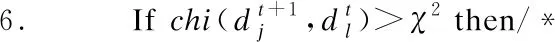
18. End While

19. End While

3.4 区间单调性分析

在SMDNS算法中通过公式(2)确保了区之间的单调性.公式(3)限制区间宽度,防止区间宽度过长.在SMDNS算法基础上,为确保融合后区间的单调性,TDD采用卡方检验来确保区间之间的单调性.但随着动态数据的不断增加,在不断融合过程中,存在两种特殊情况：区间不合理合并和区间不合理分裂.

随着动态数据不断融合,导致相邻两个区间中数据分布趋近一致,造成原本相互独立的两个区间合并为一个大区间.面对不合理合并,TDD在动态融合过程中会有自我矫正的过程.当进行不合理合并后,在下一次融合过程中,新区间与融合后的大区间之间存在明显的不一致性,进而将错误融合的大区间分裂成两个区间,实现区间融合中的自我矫正.

区间不合理分裂指融合过程中,小区间与其相交的大区间存在不一致性,导致大区间进行分裂.不合理小区间的存在是因为原始数据缺失造成的.此类小区间通常具有区间内样本数量少或样本分布不稳定的特性.虽然TDD无法判定小区间的合理性,但随着动态融合过程中数据总量的增加,各个区间中对应的总样本量也会逐渐增加.而不合理的小区间中样本数量基本维持不变.因此，当不合理区间样本数量占比低的情况下,TDD会将此类小区间视为一种噪音,并将噪音转化为空白区间.

4 实验分析

本节进行多组实验对TDD算法进行性能分析.为了验证TDD算法具有一定的有效性,本文使用了8个数据集和4个对比算法.其中8个数据集分别是Heart、Australian、Diabetes、German、Segment、Shuttle、Setimage、Vehicle.为了使实验结果更加公平,本文采用十折交叉法,将数据集均匀划分成十等份,采用9：1的比例生成训练集和相对应的测试集.本文为体现动态数据的特性,因此,选择将训练集拆分的方式,渐进式的进行动态数据离散实验.

实验中,数据集Heart、Australian、Diabetes、German、Segment在内存为8G RAM和CPU频率为2.70GHz计算机上运行,程序的开发平台为Microsoft Visual Studio 2017,使用C++语言进行程序开发.Shuttle、Setimage、Vehicle数据在内存为80G RAM和CPU频率为2.10GHz计算机上运行.表2给出了8个数据集的基本信息.

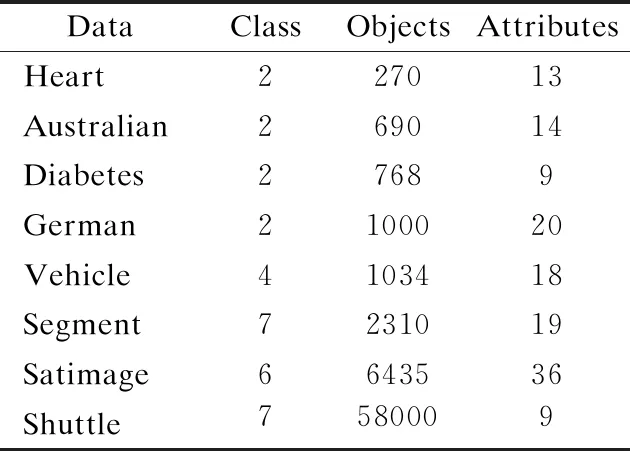
表2 UCI数据集

本实验共涉及5个离散算法,其中除了本文提出的TDD算法外,还有SMDNS,SMD两个基于粗糙集的离散算法；第4个算法是CACC算法[24],该算法与TDD算法均为多目标离散算法,不过CACC是一种静态算法；由于目前动态离散算法较少,本实验选择2006年基于模糊集的动态离散算法FTPS[14]进行对比实验.Continuous代表的不经离散处理的原始数据集直接运用C4.5[25]进行分类处理.

4.1 准确率对比实验

首先将本文算法TDD与3个静态离散算法进行对比实验,利用C4.5训练离散后的训练集,建立树进行分类处理,如表3所示,整体上可以看出可见本文TDD在Heart、Australian、Diabetes、German 4个数据集上表现良好,在与其他4个离散算法相比,平均准确率均明显偏高.数据Vehicle上,所有离散算法结果均出现大幅度的波动,其原因是十折交叉法所生成的训练集上存在差异,促使实验波动大.在数据集Segment上,平均准确率最高的是Continuous.Continuous代表的不经过离散处理的原始数据集虽然在数据集Segment上,Continuous平均准确率表现最佳,但是并不代表离散过程的不重要.

表3 C4.5分类测试样本准确率与召回率表(%)1

如表3所示,括号中数值表示平均召回率.通过Continuous训练集训练后的C4.5树模型泛化性较低,测试样本中,有大量样本数据未能成功得到分类.由此可见数据离散化的重要性.以Segment数据集为例,虽然Continuous平均准确率高达94.91%,但是平均召回率只有20.5%,说明Continuous存在很大的局限性；采用本文TDD算法后,平均召回率调高至83.3%,并且平均准确率有89.31%.

表4为本文TDD与SMDNS、CACC对数据进行离散处理所花费的时间表.从表中可见,TDD大幅度提升生了离散速度.时间大幅度减少的原因主要是本文的TDD算法利用新旧数据的离散区间融合,实现迭代式动态离散,而不是传统的将原始数据整合后重新离散化.从实验结果可证明TDD节约了时间代价.

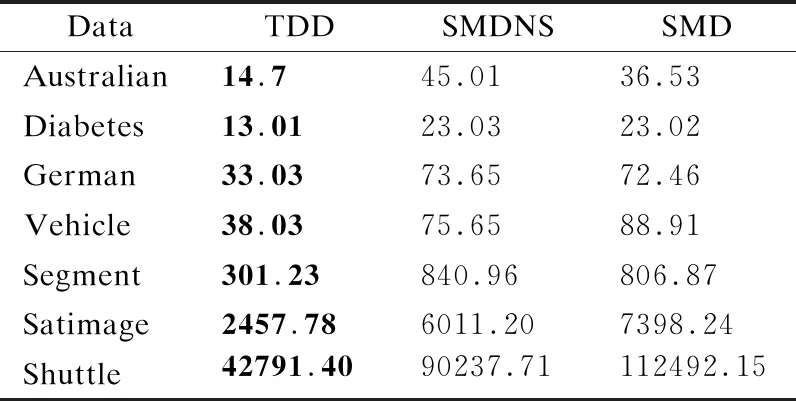
表4 数据离散预处理时间表(s)

表5中,算法ITFP相关实验数据来自文献[12]中.ITFP算法与本文TSDD算法均属于动态离散算法.从对比实验结果来看,TSDD在Australian,Vehicle,Shuttle 3个数据集上优于ITFP.实验结果并不是全部优于ITFP.说明TSDD算法还是存在很大改进.我们将会在下一个实验进行讨论.

表5 C4.5分类测试样本平均准确率表(%)

4.2 空白区间处理方案对比实验

本实验为检验空白区间不同处理方式是否对离散结果产生影响.对空白区间分别采用传统均值法,以及权值法对空白区间进行对比实验.传统的分配方法是对空白区域使用均值方法.均值法是取相邻区间边界点的均值作为新的边界点.另一种分配方法是基于宽度的权重方法,如公式(9)所示.

(9)

在表6中,对于不同的数据集,在分配空白区域的不同策略上有一定的改进.例如,在Segment中,平均方法的准确率是89.31%,召回率是83.3%.权重法的准确率为89.76%.重量法的平均样品识别率为87.1%.尽管两种方法的准确率没有太大差异.但是,均值方法的方差是5.06,权重方法的方差是1.42.可以看出,在Diabetes,German,Segment,Satimage,Shuttle的情况下,加权方法更加稳定.在正确比率相差不大的情况下,选择方差值小的方法很重要.

表6 C4.5分类测试样本准确率与召回率表(%)2

5 总 结

传统离散化模型是针对静态数据的离散化.然而现实生活中数据是呈增量式的.并且由于动态数据本身的不确定性,导致离散化过程中区间边界点的不确定,对动态区间融合过程造成一定困难.因此,本文提出了一种基于三支决策的动态离散方法TDD.相较于静态数据下的离散研究,我们考虑的是动态数据下的离散研究.本文的TDD方法也可以处理由于样本数据过多,分批次处理样本数据的情况,节约处理时间.在本文TDD方法中,通过对三支离散区间的刻画,实现了对动态数据离散过程中确定的核区间与不确定的空白区间的划分.通过卡方检验区间之间的一致性,实现了新旧离散区间集中确定的核区间集的融合操作.针对不确定性较高的空白区间,本文使用传统的均值法和宽度权值法实现对空白区间的分配.本文TDD方法在UCI上的8个真实数据集进行了验证.实验结果表明本文的方法对于处理增量式数据离散化的问题具有较好的效果.