一种利用SPXY采样的标签噪声主动清洗方法

门昌骞，孟晓超，姜高霞，王文剑，2

1(山西大学 计算机与信息技术学院，太原 030006) 2(计算智能与中文信息处理教育部重点实验室，太原 030006)

1 引 言

在机器学习中，模型的泛化性能评估指标对模型的选择具有重要的指导意义，它代表了在训练集上训练出的模型对未知数据的预测能力[1].当模型过于简单或者数据量不足时，模型泛化能力过于弱会导致欠拟合;当训练集中含有大量噪声数据或数据量过高时，模型泛化能力过于强会导致过拟合.为了解决这些问题，当训练样本不充足时，可以采用重采样(Bootstrap Sampling)[2]或交叉验证(Cross-Validation)[3]的数据划分方法来进行模型的训练;当训练样本量大或噪声含量过高时，为了防止过拟合可以采用子采样(Subsampling)[4]的数据划分[5]方法来进行模型的训练，使抽取出的样本子集具有代表性.

目前常用的样本子集采样方法[6]根据抽样准则的不同可以划分为子集同分布和子集异分布两种方式.子集同分布方式又可以分为经典抽样方法和距离划分的抽样方法，现有的经典抽样方法有随机抽样(Random Sampling，RS)、分层抽样(Stratified Sampling)、系统抽样和整群抽样[7-9]等;现有的距离划分的抽样方法有Kohonen网络法(K-H法)、K-S(Kennard-Stone)法、SPXY(Sample Set Partitioning based on Joint X-Y Distance)法、DPS(Density-Preserving Sampling)法[10-12]等;通过这些采样方法抽取出的子集样本具有全集代表性.子集异分布方式通常为聚类划分的抽样方法，如二分K-means聚类划分方法以及其它聚类方法[13-15];通过这些采样方法抽取出的子集样本差异性最大.为了选取出的样本子集具有较高的代表性，通常采用子集同分布的采样方式，经典抽样方法虽然比较简单，但效果一般不如距离划分的抽样方法：随机抽样不适用于小样本数据且稳定性较差，分层抽样一般需要考虑类别分布，系统抽样具有固定间隔的特点，一般不适用于周期性数据，而整群抽样对于群间差异性大的数据效果较差;基于距离划分的抽样方法如KH、KS、SPXY、DPS等[10-12]方式来划分确定样本的数量，而且样本分布比较均匀，具有一定的代表性，因此对数据的划分效果比较好.而现有研究表明，SPXY采样方法[10，12]选取的训练集建立的模型优于其他3种方法.

基于主动学习的标签噪声清洗方法(Active Label Noise Cleaning，ALNC)[16]虽然有很好的噪声识别效果，但是筛选出的疑似噪声样本中仍含有一定比例的非噪声样本.这一问题的原因有如下两个方面：首先在选取一定比例的初始样本时，随机选取出的样本子集不具有代表性，使得初始模型的泛化能力较差，进而影响后续样本的选择;另外，在通过主动学习选取疑似噪声样本时，查询策略只考虑样本的不确定性，而不考虑样本的代表性，从而影响了模型更新过程中的泛化性能的提升.为了解决这一问题，本文提出一种基于SPXY采样的标签噪声主动清洗方法(Active Label Noise Cleaning based on SPXY，SPXY_ALNC)，该方法在主动学习初始样本的选择过程中采用SPXY采样方法，并且在主动学习筛选疑似噪声样本的过程中将不确定性采样与SPXY采样方法相结合，使初始模型具有较好的泛化性能，同时提高了模型在更新过程中泛化性能的提升，进一步有效降低了人工专家的额外标记代价.

2 SPXY_ALNC算法

2.1 SPXY_ALNC方法简介

基于SPXY采样的标签噪声主动清洗方法是在基于主动学习的标签噪声清洗方法[16]上进行的改进.在原来方法的基础上，通过与SPXY采样方法相结合，在模型初始阶段选出的训练样本更具有代表性，使初始模型具有更好的预测效果，并且在后续样本的筛选过程中，不确定性采样与SPXY采样相结合，使筛选出的样本既有不确定性又具有代表性，从而提高了模型在不断更新过程中的改善效果，达到更好的将标签噪声样本筛选出来的目的.

2.2 算法基本原理

训练集被认为是人工未检验样本集，由标记正确样本以及标记错误样本所组成，先利用SPXY采样方法选择一定比例的样本，假设p，q为N个训练样本中的一对样本，则SPXY采样方法的距离计算公式为：

(1)

其中，

(2)

(3)

先利用专家对SPXY采样所得数据进行标记，将标记好的样本集记为XL，利用该初始样本集进行模型训练，得到初始的基学习器.然后通过得到的基学习器对其余未检验样本的预测结果进行评估，利用公式(4)选出对于模型θ置信度最低的未检验样本xs交给人工专家进行标注：

(4)

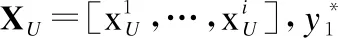
(5)

这样在每一轮查询选择过程中只对所求交集中的样本进行评估，达到快速选择样本的目的，同时既考虑到样本的不确定性又考虑到样本的代表性，使主动学习查询选择样本的过程中模型提升效果更加明显.

在每一轮迭代中，由于训练样本集的规模和质量都在提升，其预测精度也在提高.令d1和d2为相邻两次不一致样本集的样本数量，由于每一次都会选择出一个样本，因此当|d2-d1|<=1时训练模型达到稳定.考虑噪声样本的干扰，以及模型在早期阶段由于性能的不稳定可能造成相邻两次预测结果会比较接近，但此时对应的不一致样本数量却比较多，算法在停止条件上设定一个阈值ε，为不一致样本集占整个样本集的比例，当d1和d2同时小于ε×n，并且值接近时算法停止.

2.3 算法步骤

算法SPXY_ALNC算法是在ALNC算法的基础上进行的改进，具体步骤如算法1所示：

算法1.SPXY_ALNC算法

输入：初始未检验训练数据集XU(大小为n)，初始采样比例r1，阈值ε;

输出：已检验样本集XL.

步骤1.从初始未检验训练集XU中，通过SPXY采样方法采样比例为r1的样本，进行人工标记，将标记好的样本添加到样本集XL中，并更新XU=XUXL;

步骤2.重复执行以下步骤：

步骤2.1.利用当前已检验样本XL训练模型，得到当前模型θ;

步骤2.2.用模型θ对当前未检验样本集XU中的样本进行预测，并选择出与训练样本集中标签不一致的样本放到当前不一致样本集XD中;

步骤2.3.通过SPXY采样方法对当前未检验样本集XU进行采样，得到采样后样本集XSPXY，求当前二者的交集X∩=XD∩XSPXY，根据公式(5)选出X∩中置信度最低的样本xs;

步骤2.4.对选出样本进行专家人工标记后并入到样本集XL中，更新XU=XUxs和XL=XL∪xs，清空XD、XSPXY和X∩;

步骤2.5.如果本次循环中标签不一致样本数量d2比上轮循环中标签不一致样本数量d1不只多一个，或d1、d2均大于ε×n，则循环继续;

步骤3.算法结束.

3 实验结果及分析

3.1 实验设置及实验数据集

本文采用和文献[16]中的数据集，包括：MNIST数据集、Letters数据集、Wine数据集以及Cancer数据集，数据集的具体描述见表1.

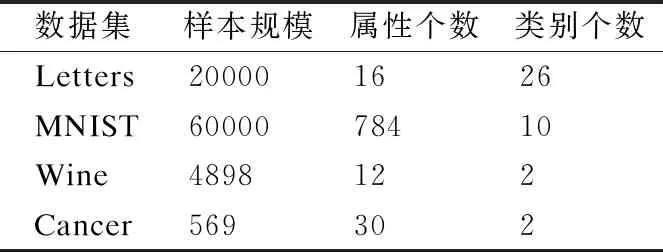
表1 原始数据集描述

数据集的采样方式为从原始数据集等比例获取正类样本和负类样本，并混合一定比例噪声.如MNIST数据集中，选取易混淆数字构成数据集，D1数据集正类数字为4，负类数字为7和9;D2数据集正类数字为7，负类数字为4和9;D3数据集正类数字为9，负类数字为7和4.以D1为例，正类数据集构成方式为：在数字4的原始样本集中选取1000个样本，将其中的100个样本(10%比例的噪声样本)构造为噪声数据(即标注为负类数字7和9各50个样本);负类数据集构成方式则是在数字7和数字9各选500个样本，然后将其中的100个标注为噪声数据(即正类数字4).其它数据集采样方式和加噪方式也类似，采样后的实验数据集见表2.

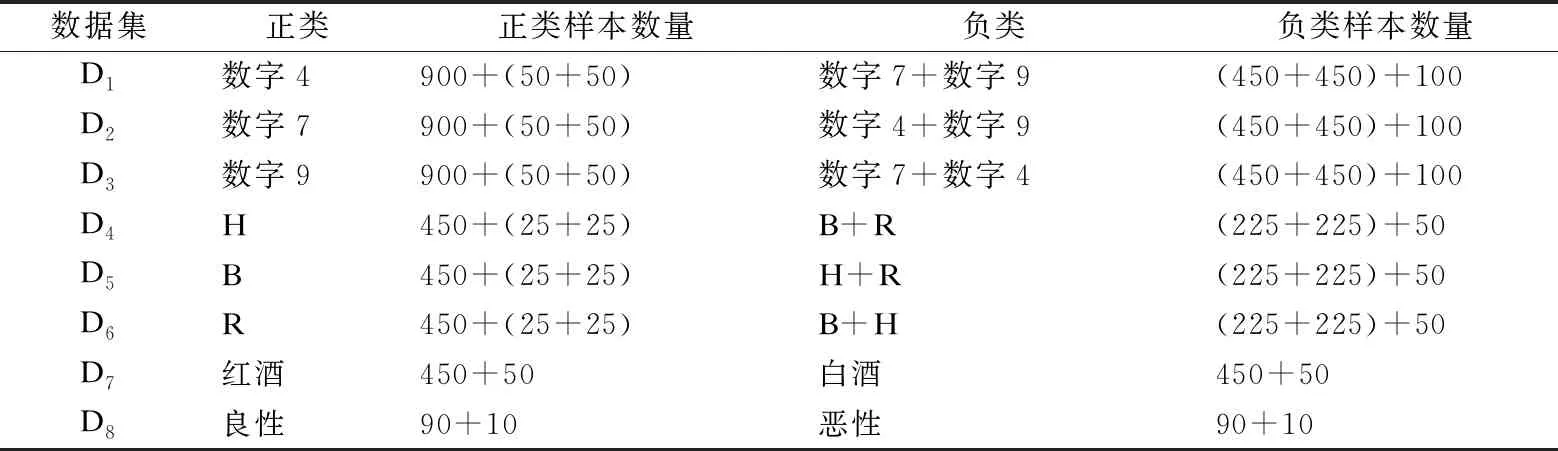
表2 采样后的实验数据集

注：D1～D6数据集中，正类样本数量m1+(n2+k2)表示由m1个正确标记的正类样本和(n2+k2)个其它两类负类样本错误标记为正类的样本组成，负类样本数量(n1+k1)+m2则由(n1+k1)个标记正确的负类样本和m2个正类样本被标记为负类的样本组成;D7～D8数据集中，正类样本数量m1+n2表示由m1个正确标记的正类样本和n2个错误标记为正类样本的负类样本组成，负类样本数量n1+m2表示由n1个正确标记的负类样本和m2个错误标记为负类样本的正类样本组成.

3.2 参数设置及评价指标

模型的参数设置以及相关评价指标仍与原来实验相同，将初始采样比例r1设定为0.05，噪声水平r2的变化设定为10%-40%，阈值ε设定为0.005.仍采用噪声清洗比例R1、人工检验代价R2和人工额外检验代价R3来评价实验中各个算法的性能;R1是指全部标签噪声样本中被人工专家更正过来的样本数量的占比，计算公式为：

(6)

其中，n1为原始样本集中噪声样本的个数，n2为加入样本集中噪声的数量，n为样本总数，R1越大，说明噪声清洗效果越好.R2为人工检验样本的数量占样本总数的比例，其计算公式为：

(7)

其中，n3为加入的样本数量.R2越小，说明人工检验样本数目越少.R3是指人工检验的样本中除了噪声外多余检验的样本占比，计算公式为：

R3=R2-r2×R1

(8)

R3越小说明人工检验样本中噪声占比越高，噪声识别越好;本文算法的改进性能主要通过该指标与原来算法进行对比.

3.3 实验结果

为了验证SPXY采样方法在模型初始化阶段与循环查询阶段均对模型识别噪声起到了改善作用，首先将ALNC方法中的初始采样方法由随机采样改变为SPXY采样，查询阶段策略保持不变，在原有数据集上进行实验，此时的实验方法为ALNC_Initial_SPXY;然后进一步采用SPXY采样与不确定性采样相结合的查询策略，在原有数据集上进行实验，此时的实验方法为SPXY_ALNC;在相同数据集上对3种不同方法进行了实验对比，为避免随机采样带来的偶然性，在每个数据集上进行5次随机采样，每次采样得到的样本进行10次重复实验，求出50次实验的平均值作为最后的实验结果.

3.3.1 噪声清洗效果比较

图1为不同噪声水平(10%-40%)下，ALNC、ALNC_Initial_SPXY以及SPXY_ALNC 3种不同噪声清洗方法在4个数据集上的噪声清洗效果.从图1中可以看出，与原有ALNC方法相比，ALNC_Initial_SPXY方法与SPXY_ALNC方法的噪声清洗比例基本保持不变.通过实验可以得出结论，本章提出的改进算法效果与原有方法接近，在此前提条件下进一步对人工额外检验代价进行比较.

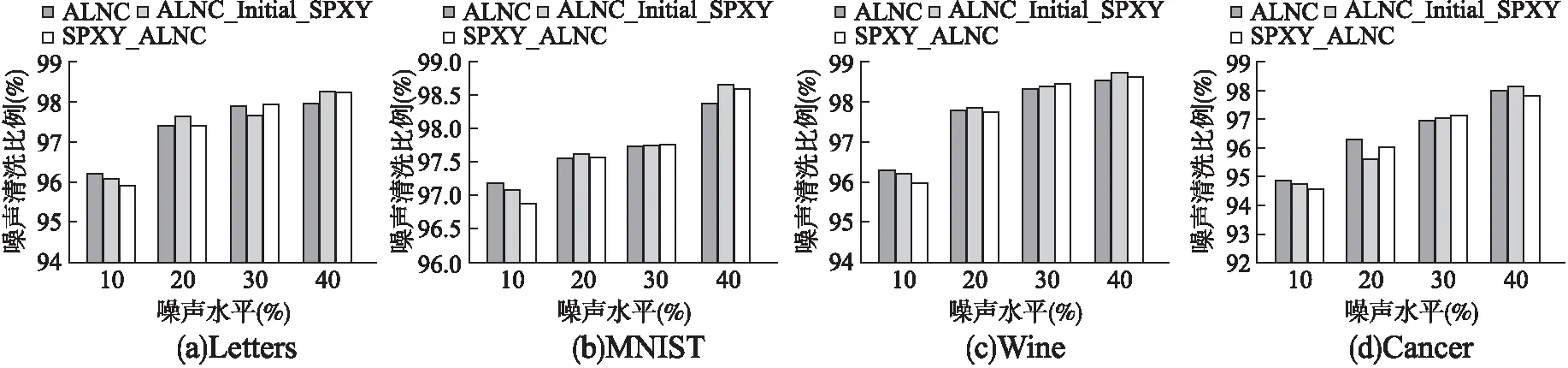
图1 不同数据集噪声清洗效果比较

3.3.2 人工额外检验代价比较

在不同噪声水平3种标签噪声主动清洗方法的噪声清洗效果相当的情况下，通过实验来进一步比较它们的人工检验代价.如图2所示，在4个不同的数据集上，3种标签噪声主动清洗方法的人工额外检验代价均随噪声水平的提高不断下降，并且可以明显看出，在不同噪声水平下ALNC_Initial_SPXY方法的人工检验代价低于原来的ALNC方法，说明改变初始化阶段的采样方式对噪声识别效果起到了一定的提升作用;而SPXY_ALNC方法在不同噪声水平下的人工检验代价又明显低于ALNC_Initial_SPXY方法，说明在循环查询阶段将不确定性采样和SPXY采样相结合，也使模型在更新过程中对标签噪声样本的识别效果得到了进一步的提升.因此，改进后的SPXY_ALNC算法与原有ALNC算法相比，对标签噪声样本具有更好的识别效果，从而降低了标签噪声主动清洗过程中的人工额外检验代价，并且在噪声水平较低的情况下，SPXY_ALNC算法与ALNC算法的人工额外检验代价相差比较大，改善效果更加明显.

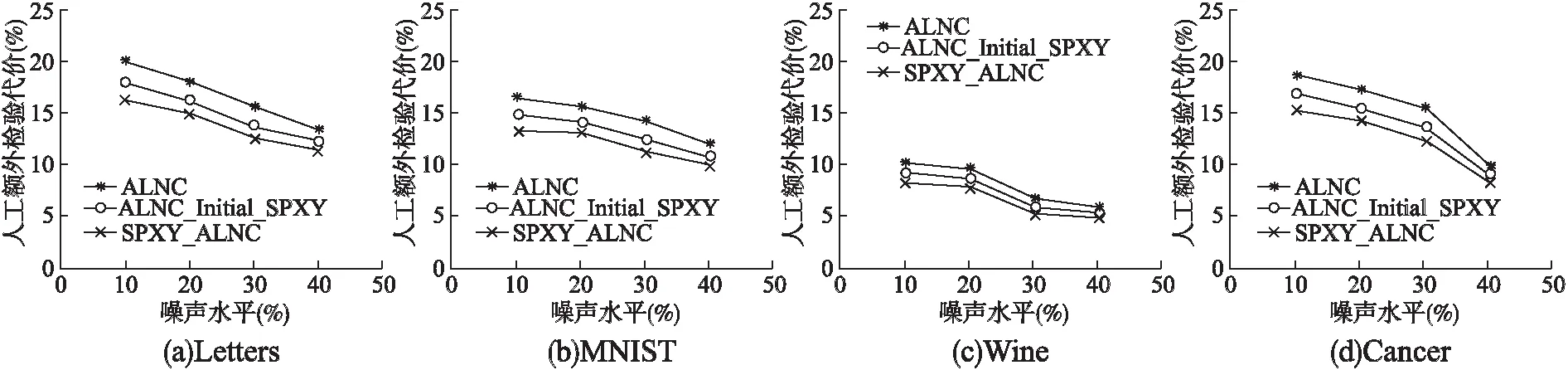
图2 不同数据集人工检验代价比较

3.3.3 不同模型的实验结果比较

由于在之前的实验中，不同方法在标签噪声主动清洗过程中均采用高斯过程分类(Gaussian Processes Classifier，GPC)[17]作为基分类器进行模型训练，对改进算法的模型独立性需要进行进一步的验证.因此采用另外两种不同的基分类器KNN和SVM在不同数据集上进行实验，对3种不同模型下的噪声清洗效果和人工额外检验代价进行对比，噪声清洗效果实验结果如表3所示，人工额外检验代价实验结果如表4所示，为了方便观察，表3和表4中的实验结果均保留两位小数.通过实验结果比较可以发现，GPC、KNN以及SVM 3种模型在每个数据集的不同噪声水平下，ALNC算法与改进后的SPXY_ALNC算法的噪声清洗效果均保持相当的水平;同样，在3种不同模型下，SPXY_ALNC算法在每个数据集中不同噪声水平的人工额外检验代价都比ALNC算法低.因此可以得出，SPXY_ALNC方法的改进效果与模型训练过程中基分类器的选择没有直接的关系，具有一定的模型独立性.并且由表4可以看出，在每个数据集上，噪声水平越低，3种模型的ALNC算法与SPXY_ALNC算法之间的人工额外检验代价的相差越大，说明在噪声水平相对较低的情况下SPXY_ALNC方法可以明显降低专家的额外检验代价.

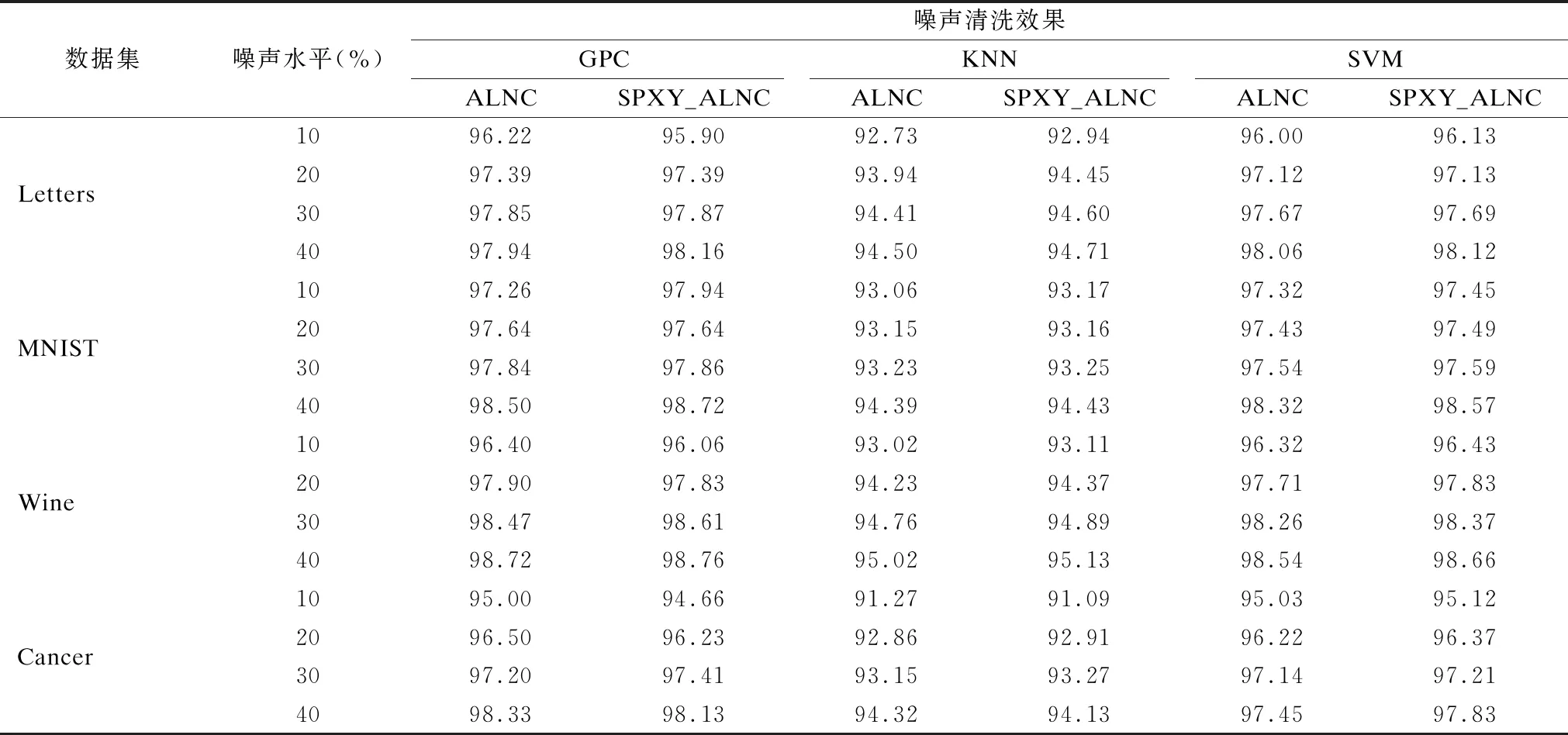
表3 不同模型下的噪声清洗效果比较

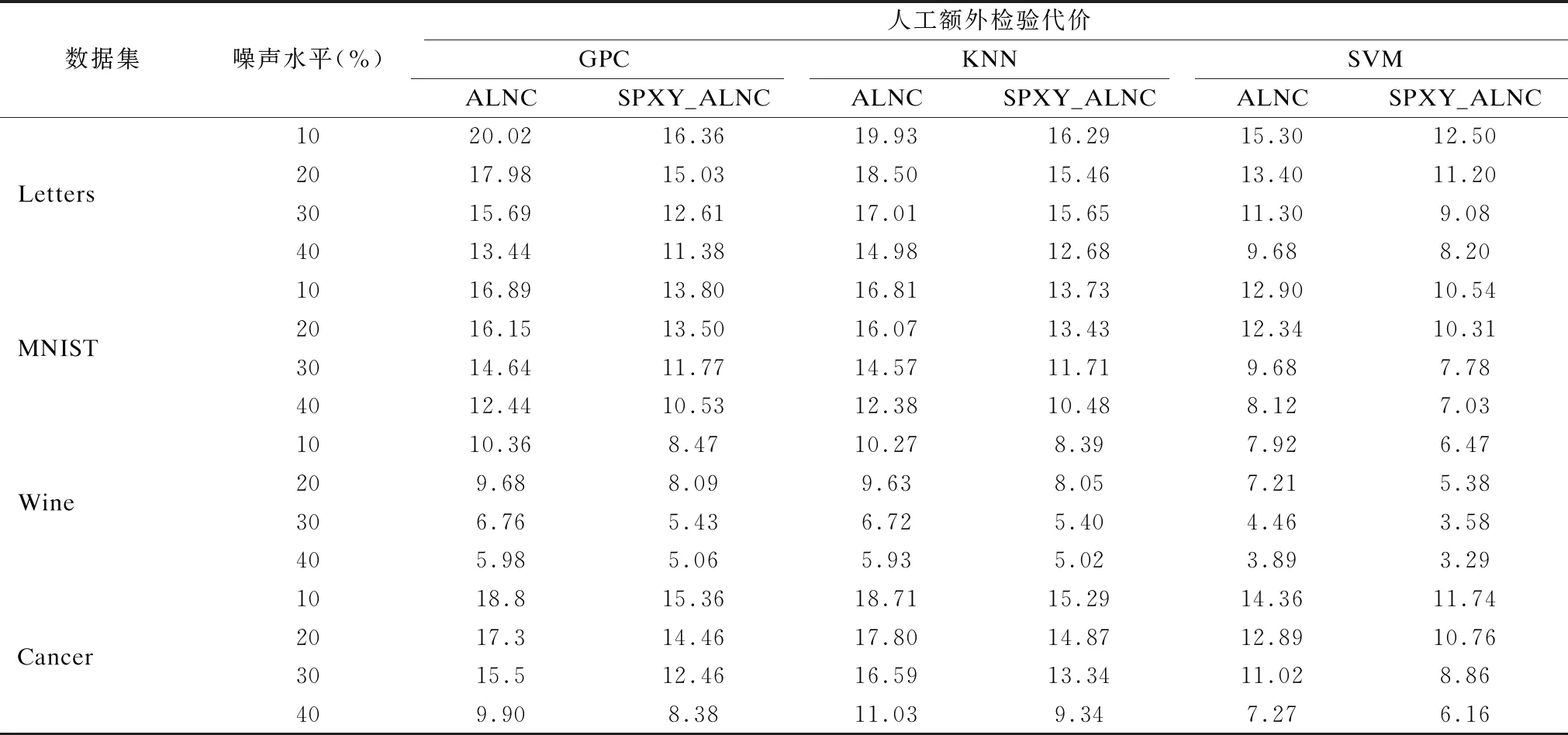
表4 不同模型下的人工检验代价

4 结束语

本文提出了一种基于SPXY采样的标签噪声主动清洗算法，首先通过SPXY采样选取一定比例的初始样本训练生成一个基分类器，然后通过在主动学习过程中将SPXY采样与不确定性采样相结合的查询策略，更好的将噪声样本筛选出来进行清洗.与ALNC算法相比，SPXY_ALNC在保持原有噪声清洗效果基本不变的前提下减少了人工额外检验代价，尤其在低噪声水平下效果更加明显，并且不受训练模型改变的影响.但是该算法仍存在时间复杂度较高的问题，并且在多分类问题中该算法的效果仍需进一步研究.