基于蒙特卡洛仿真的机场值机系统优化研究
王加冕,陶翼飞,罗俊斌,张 源
(1.昆明理工大学机电工程学院;2.昆明昆船逻根机场物流系统有限公司,云南昆明 650500)
0 引言
航空运输具有快速、高效的优点[1]。机场值机主要负责帮助旅客办理登记牌和行李托运,是机场对旅客服务的重要环节。有效优化机场值机,可以提高机场服务效率,提升顾客服务满意度。因此,对机场值机系统的研究具有重要意义。
目前,国内外很多学者对机场值机和管理问题作出了探究。在研究旅客排队方式上,Ding 等[2]、Sun[3]在队列长度、排队方式的定性和定量关系方面进行研究;邢志伟等[4]引入时序概念对排队过程作离散化处理,得到蛇形排队形式下的队列长度马尔科夫链,以单航班离港旅客聚集模型预测每个时序的聚集速率,并通过选定值机柜台服务率的合适值,建立开放固定数量值机柜台情况下多个邻近航班值机排队长度模型;Kierzkowski 等[5]、黄海洋等[6]使用Flex⁃sim 仿真软件在M/M/1 的排队形式下建立了基于动态管理的自助值机系统模型,并通过设置顾客可接受的最大等待时间和最大排队长度对自助值机柜台进行优化,但没有研究排队形式为M/M/c 的情况;文献[7-11]针对行李处理系统、中转换乘推荐系统、机场陆侧行人交通等方面进行优化,以提高服务效率;张洋[12]利用离散事件仿真模型准确量化机场内的需求和供给,充分考虑旅客体验,实时根据机场用户需求变化,提前评价设备设施表现变化,为机场决策提供辅助支持;衡红军等[13]、刘一等[14]对旅客到达预测及客流特征进行研究;针对服务窗口和柜台,宫宇姝[15]、柳泽原等[16]通过优化不同柜台或窗口的分配方式提高服务效率;张天炫等[17]通过研究排队方式与服务柜台的关系对服务效率进行优化;潘恒毅[18]、杨洋等[19]通过增设备用服务台或专用服务窗口,提高顾客满意度。
上述研究通过改变值机排队方式或优化机场相关服务系统等提高机场服务满意度,对机场值机柜台资源配置的研究较少,一般通过调整不同类型的柜台分配方式进行优化。本文以机场值机系统为研究对象,通过蒙特卡洛仿真,统计机场值机现有数据,建立参数化仿真模型,分析系统稳态下不同值机柜台开放数量对应的旅客排队人数、等待时间等数据,结合不同柜台数量的单位时间成本,对选择最佳的值机柜台开放数量,提出合理的优化建议。
1 机场值机排队系统特征及影响因素
1.1 值机系统特征与假设
机场值机包括人工和自助两个部分,为了简化模型,本文主要研究经济舱旅客办理值机的人工服务柜台。一个值机单元由以下3 部分组成:①输入过程,将机场值机排队系统看作无限源系统,旅客随机进入系统中,且到达的时间间隔相互独立;②排队规则,进入值机排队系统的旅客会选择排队人数较短的柜台进行排队,遵循先到先服务的服务规则;③服务机构,机场有c 个值机柜台,它们相互并联,每位旅客可以在任意一个柜台排队办理值机,且一个柜台只能依次服务一个旅客。
机场值机排队属于离散事件,在该系统中,输入的对象为旅客,旅客进入机场航站楼选择最短队列排队,值机完成后离开并进行安检候机,流程如图1 所示。

Fig.1 Airport check-in process图1 机场值机流程
本文对排队模型进行如下假设:①在一天内的任何一个单位时段内,到达值机排队系统的旅客服从泊松分布,旅客到达机场航站楼进行值机的时间间隔服从负指数分布;②每个值机柜台服务水平相同。
1.2 值机排队系统影响因素
值机排队系统是旅客在机场站内等待时间较长的区域,办理值机和托运的能力是旅客对机场服务满意度的重要因素之一。一方面与办理值机的工作人员工作效率和行李系统分拣能力有关;另一方面则与机场的值机管理和资源配置有关,例如开放的值机柜台数量。本文主要针对后者进行研究分析。
2 值机系统相关数学模型建立
2.1 值机系统单位时间成本
值机系统的单位时间成本由两部分组成:①服务台工作单位时间成本;②旅客等待时间成本。
相关参数表达如表1 所示。

Table 1 Definition parameters of unit time cost mathematical model表1 单位时间成本数学模型定义参数
数学模型如下:
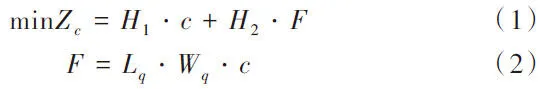
假设最优解为c':

将式(1)代入式(3)、式(4),可得:
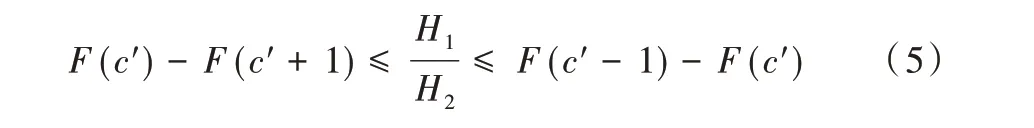
在不考虑设备折旧成本情况下,分别求出c=1,2,3,4…时的F 值,得到c'。
2.2 系统稳态下的值机柜台数量
机场值机系统是一个离散事件系统,研究中需要确保系统处于一个平衡的状态以确定柜台数量。由排队论可知,单服务强度和系统稳态概率参数如表2 所示。

Table 2 Parameter definitions of steady-state mathematical model of the system表2 系统稳态数学模型定义参数
则单服务强度:

系统稳态概率:
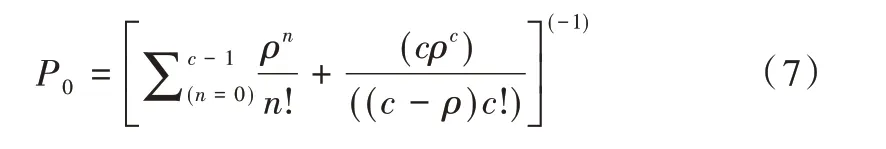
稳态下的柜台数量应满足约束条件为:

2.3 旅客平均到达率
旅客平均到达率是实现仿真建模的重要参数,决定模型中旅客源的生成分布。根据实际数据和对数据的拟合优度检验,确定平均到达率符合泊松分布,根据泊松分布函数,采用极大似然估计法,求得旅客平均到达率参数如表3 所示。

Table 3 Parameters definition of passenger arrival rate mathematical model表3 旅客到达率数学模型定义参数
泊松分布概率:
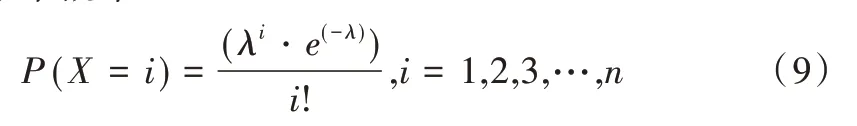
极大似然函数:
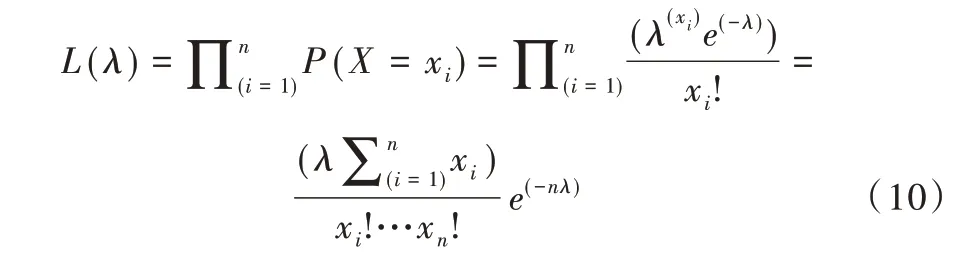
经推导,旅客的平均到达率:
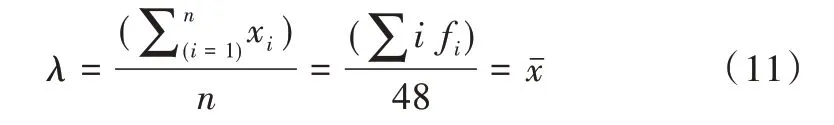
2.4 旅客平均服务率
仿真模型中服务柜台工作效率体现在旅客平均服务率上,求得平均服务率即可确定柜台工作参数。根据数据的拟合优度检验,确定平均服务率符合负指数分布,采用极大似然估计法,求得旅客平均服务率参数如表4 所示。

Table 4 Parameters definition of passenger service rate mathematical model表4 旅客服务率数学模型定义参数
总体T 服从参数为μ的负指数分布,则有概率密度函数:
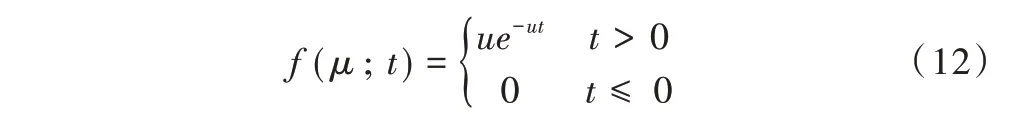
似然函数:
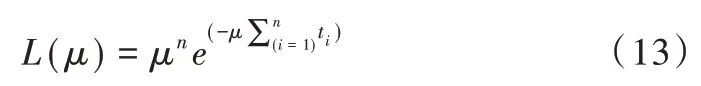
对似然函数取对数:
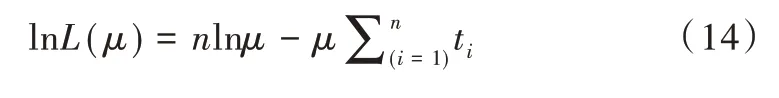
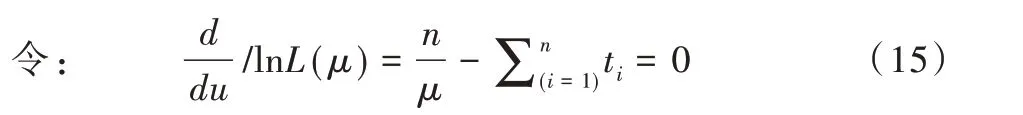
解得μ的极大似然估计值:
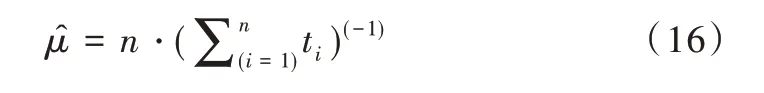
3 机场值机系统建模与仿真分析
蒙特卡洛仿真基本假设主要在于一定数量的重复实验,某一事件出现的频率近似等于事件出现的概率。本文以某民航机场的一个值机岛为例,由于机场排队是离散动态系统,旅客因素较多且不易用数学模型表示,故采用蒙特卡洛方法求解。采用仿真软件Plant simulation 构建参数化仿真模型,按蒙特卡洛方法对旅客携带的行李数量和旅客进入的值机柜台序号进行大量随机仿真实验,求得更接近真实情况的实验结果。
3.1 旅客源与值机柜台设置
收集机场某工作日实际数据,统计每小时到达机场值机柜台的旅客数(人/小时),并记录其中500 位旅客值机过程中的服务时间,通过问卷调查的形式得到旅客能接受的最大排队长度。整理原始数据得到每小时到达值机柜台旅客数的统计情况如表5 所示,值机服务时间统计如表6所示。
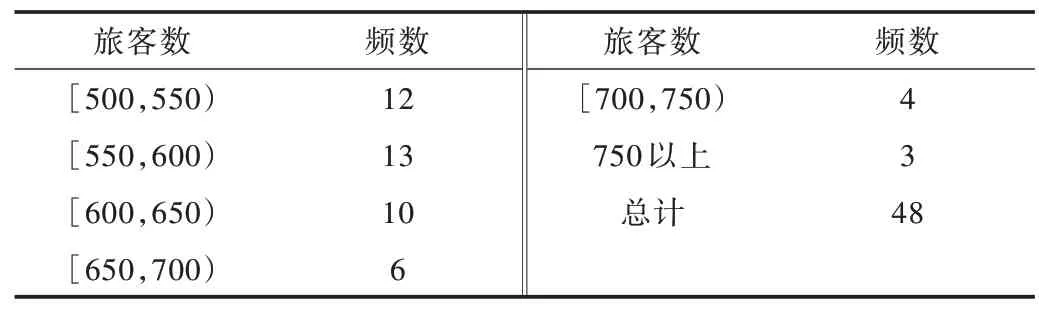
Table 5 Statistics of the number of passengers arriving in a unit time period表5 单位时间段内旅客到达数量情况统计
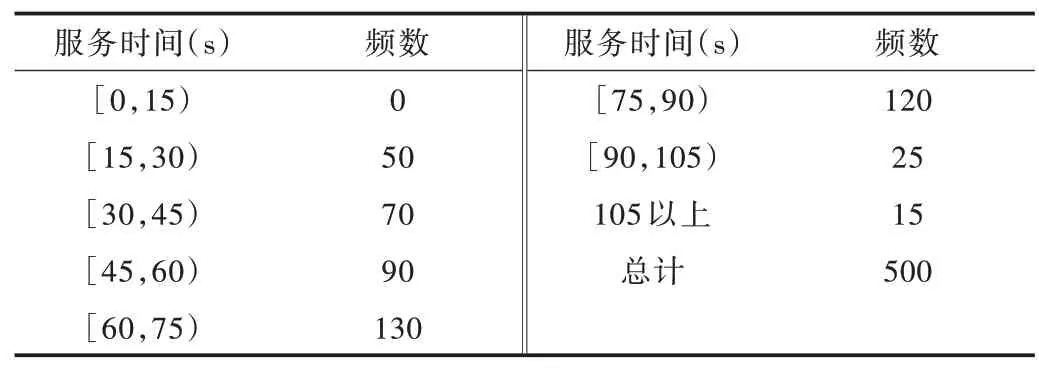
Table 6 Passenger service time statistics表6 旅客服务时间统计
对表5、表6 数据进行拟合度检验,结果如表7 所示。

Table 7 Poisson distribution goodness of fit test of arriving passengers表7 旅客到达的泊松分布拟合优度检验
由表7 可知,拟合优度检验P值为0.073,大于0.05,旅客到达符合泊松分布,假设成立;由表8 可知,拟合优度检验P值为0.441,大于0.05,旅客服务时间符合负指数分布,假设成立。
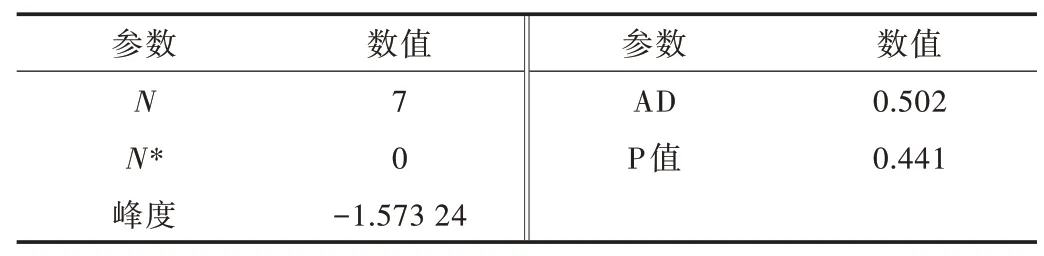
Table 8 Goodness of fit test of exponential distribution of service time表8 服务时间的指数分布拟合优度检验
根据式(11)可以得到单位时间内到达航站楼值机柜台的旅客平均到达率λ=610.426 7 人/h=10.173 6 人/min。对表6 数据进行分析,根据式(16)可以得到旅客平均服务率μ=0.015 1 人/s=0.906 人/min。模型参数设定:旅客平均到达率为λ=10 的泊松分布;机场柜台服务效率为μ=0.9的负指数分布。
3.2 值机过程仿真
本文所建值机岛模型,共有20 个服务台,其中负责普通旅客值机的服务台为18 个,当服务普通旅客的值机台同时开放时,仿真界面如图2 所示,值机旅客的最大排队人数和旅客平均时间如表9 所示。

Fig.2 Simulation interface of full counter opening图2 柜台全部开放仿真界面
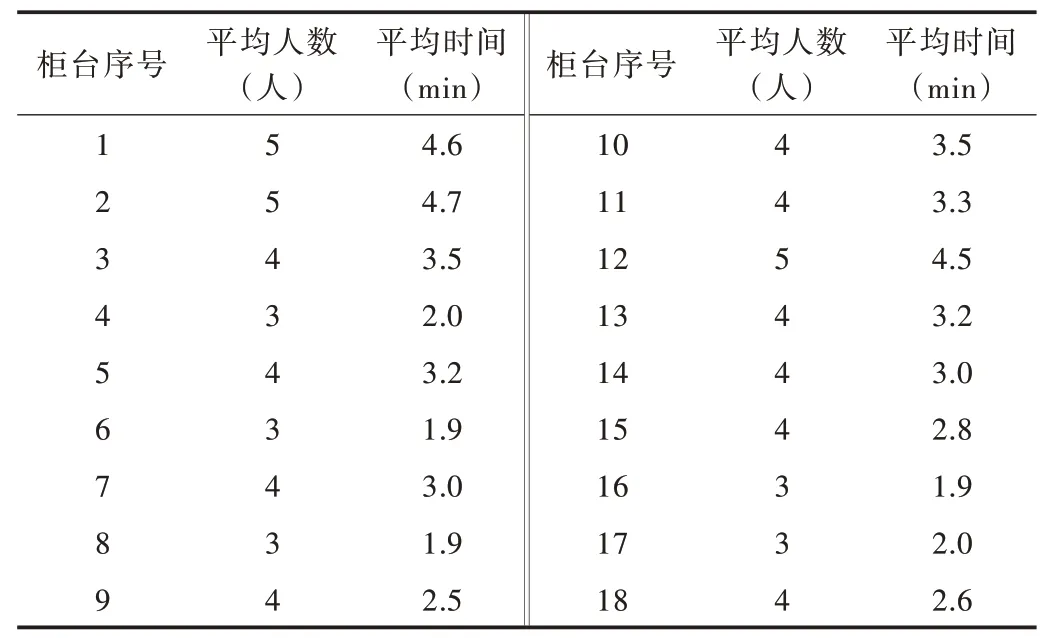
Table 9 Queuing situation when fully opened表9 全开通时的排队情况
由表9 可得,当普通旅客窗口全部开放时,旅客排队的平均人数为3.9 人,平均等待时间为3.01min,代入式(2),得开放18 台值机柜台时的单位时间内旅客等待总时长为3.52h,代入式(1),得单位时间总成本48.52H2。
该机场一般开放普通旅客值机服务台8~10 个,即每边有4~5 个服务台运行,通过仿真得到值机旅客的最大排队人数和旅客平均时间如表10 所示。
由表10 可得,开放10 台值机柜台时平均排队人数为13.1 人,旅客的平均等待时间为13.64min,代入式(2),得到单位时间内旅客等待总时长为29.78h。
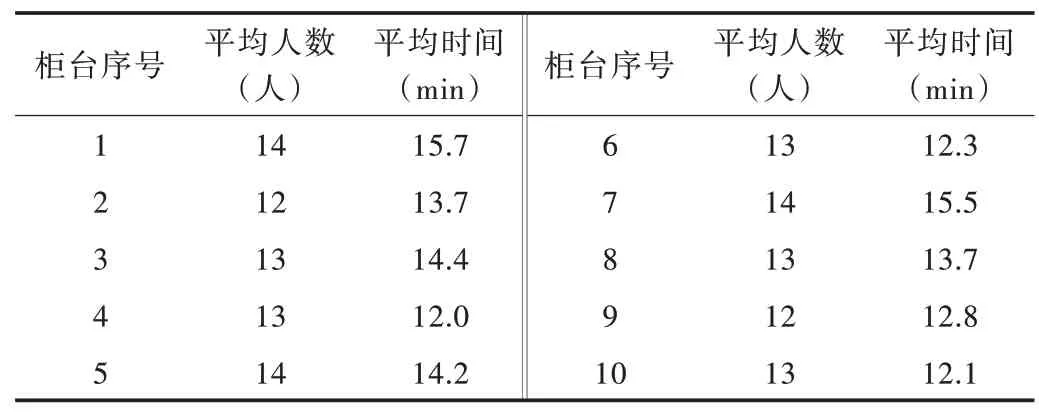
Table 10 Queuing situation when opening 10 check-in counters表10 开放10 个值机柜台时的排队情况
从仿真结果可以看出,开放10 台值机柜台时,排队等候人数较多,时间较长;开放全部值机柜台时,虽然使得旅客的服务效率得到较大提升,但所产生的成本较高。因此,选择一个合适的值机柜台开放数量比较重要。
3.3 过程优化及分析
本文随机对100 个旅客进行问卷调查,统计旅客能接受的最长排队长度,数据如表11 所示。
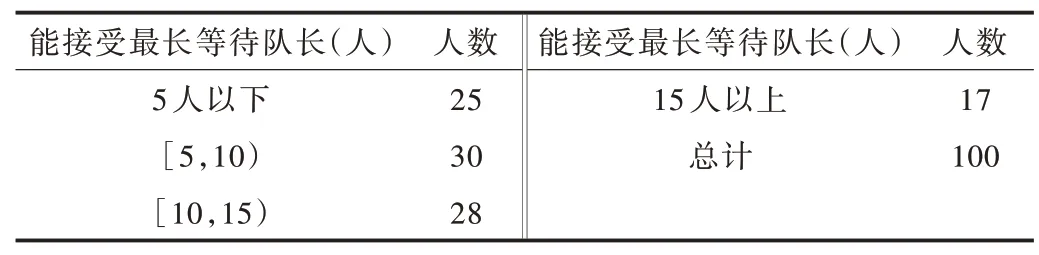
Table 11 Statistics of the longest queuing length acceptable to passengers表11 旅客能接受的最长排队等待长度统计情况
经计算可得,旅客能接受的最大排队长度为:
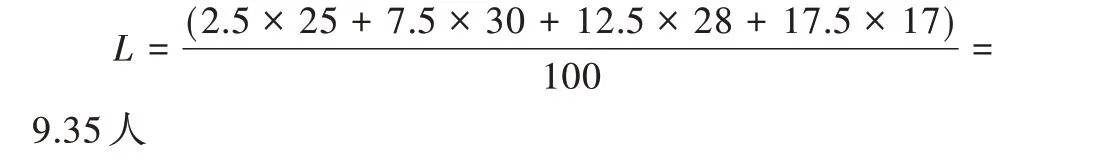
经研究可知,顾客等待时间的情绪描述[22]如表12 所示。

Table 12 Psychological description of customer waiting time表12 顾客等待时间的心理描述
经研究论证,顾客接受等待时间范围是5~10min,顾客的期望等待时间T=6min。
根据式(8),当Pc<1 时,求得c>11.23,即至少有12个值机柜台时,系统才能在稳态下运行。负责值机的工作人员一天需要2~3 人轮换,因此。对开放12~17台值机柜台进行多次仿真实验,得到不同值机柜台数量下的各项数据,取平均值如表13 所示。
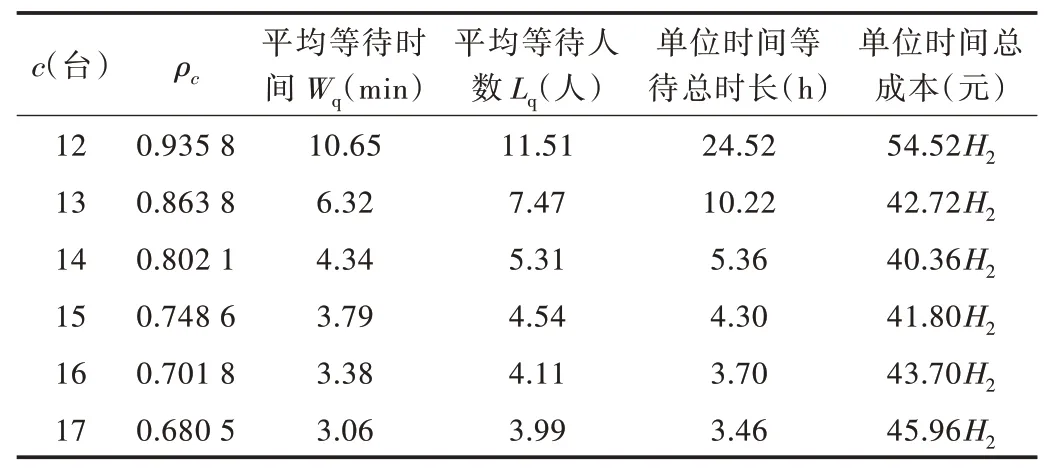
Table 13 Indicator values of different check-in counters表13 不同值机柜台数下各指标值
可以看出,从旅客服务的感受考虑,满足Wq≤6min,Lq≤9.35 人的条件下,开放普通旅客值机柜台数量最少为14 时,旅客平均等待时间为4.34min,平均排队人数为5.31人。在尽量满足旅客感受的同时,从时间成本考虑,由表13 仿真数据可得,当c=14 时,F(14) -F(15),此时单位时间总成本最低。
综上所述,从旅客满意度和值机系统总费用两方面综合考虑,确定出最佳值机柜台数量c'=14。
4 结语
本文对机场值机系统的服务能力进行研究,建立机场值机柜台服务仿真模型,基于蒙特卡洛仿真原理统计分析值机系统服务能力。在值机系统的稳态下,对开放不同服务值机柜台数量的排队人数和平均等待时间进行仿真分析,优化合理的值机柜台配置方案。实验结果表明,开放合理的值机柜台能够降低值机排队的人数和旅客等待时间,提升旅客服务满意度,使得值机服务效率得到较大提升,并且降低机场和旅客单位时间消耗总成本。
——国外课堂互动等待时间研究的现状与启示

