LCC-HVDC系统直流控制回路小干扰稳定性分析

叶运铭，汪娟娟，陈 威，丁天皓，周盛宇，傅 闯

（1.华南理工大学电力学院，广东省广州市 510641；2.直流输电技术国家重点实验室（南方电网科学研究院有限责任公司），广东省广州市 510663）

0 引言

中国能源资源逆向分布的特点决定了其“西电东送”和“北电南送”的输电格局［1-2］。为了实现跨区域资源优化配置，具有远距离、大容量特点的电网换相换流器高压直流（line commutated converter based high voltage direct current，LCC-HVDC）输电得到了充分的发展［3］。然而，随着LCC-HVDC系统传输容量不断增加，受端交流电网的强度逐渐减弱，此时系统易出现振荡发散及换相失败［4-6］等问题，严重威胁系统的安全稳定运行。因此，对LCC-HVDC系统的稳定性进行分析，具有重要意义。

基于小干扰动态模型对系统进行稳定性分析是研究交直流混联电力系统稳定性的基本方法［7-14］。文献［8-9］建立了LCC-HVDC逆变侧系统的小干扰动态模型，基于特征值分析法及参与因子指标，针对定关断角和定电压2种不同控制策略下系统的小干扰稳定性进行了分析。文献［10］基于质量-阻尼-弹簧概念提出了一种LCC-HVDC系统的线性化模型，便于采用经典模式分析等线性分析工具进行系统稳定性分析。文献［11］提出了一种基于改进动态相量的LCC-HVDC线性化模型，并采用特征值分析法分析了控制器比例-积分（PI）环节参数对系统稳定性的影响。文献［12］采用特征值分析法、灵敏度及参与因子指标研究了定电压及预测型定关断角控制对LCC-HVDC小干扰稳定性的影响。文献［13-14］采用特征值分析法揭示了系统参数对整流侧采用LCC、逆变侧采用电压源换流器（voltage source converter，VSC）和模块化多电平换流器（modular multilevel converter，MMC）的混合型直流输电系统小干扰稳定性的影响。上述文献对LCCHVDC系统进行稳定性分析得出的结论大多是定性结论，尽管通过特征值分析法及参与因子指标等可以揭示参数变化时系统稳定性的变化趋势以及与失稳模式强相关的状态变量，但却难以进一步解释系统失稳的机理。因此，LCC-HVDC系统的失稳机理亟待进一步研究。

基于传递函数模型对交直流混联电力系统的稳定性及控制器间的交互作用进行分析，能够较为深入地揭示内在机理［15-20］。文献［15］推导了VSC并网系统的外环有功控制传递函数，揭示了锁相环（PLL）带宽、定交流电压带宽等参数对外环有功控制稳定性的影响。文献［16］推导了VSC并网系统电流内环控制的线性化闭环表达式，揭示了PLL与电流内环控制间的交互作用。文献［17］建立了VSC-HVDC的多输入多输出（multi-input multioutput，MIMO）传递函数矩阵模型，探究了不同控制回路的稳定性及控制回路间的交互作用。文献［18］建立了混合双馈入直流输电的等效定有功功率及定无功功率的传递函数，定量评估了不同系统参数对各控制回路小干扰稳定性的影响。文献［19］以LCC逆变站为例，研究了不同控制回路被控对象右半平面（right half plane，RHP）零点的分布规律及其对各自独立控制回路小干扰稳定性的影响。文献［20］提出了多馈入LCC-HVDC系统的单输入单输出（single-input single-output，SISO）等值模型，可用于分析换流站间的交互作用对直流电流稳定性的影响。将MIMO系统简化为SISO的研究方法应用于LCC-HVDC系统中，能够建立LCC直流控制回路的传递函数模型，进一步揭示系统参数对LCCHVDC直流控制回路稳定裕度的具体影响。

本文研究对象为整流侧采用定直流电流控制策略、逆变侧采用定直流电压控制策略的LCC-HVDC系统。首先，推导了LCC-HVDC系统的时域线性化模型，并对其进行Laplace变换，建立了直流控制回路的传递函数模型。然后，应用经典控制理论，采用增益裕度（gain margin，GM）、相位裕度（phase margin，PM）和灵敏度函数最大峰值指标，定量评估了直流控制回路带宽、逆变侧PLL带宽和逆变侧交流电网强度对各直流控制回路小干扰稳定性的影响。最后，揭示了不同系统参数下各直流控制回路稳定裕度的具体变化规律，所得结论对LCC-HVDC输电系统的控制器参数整定具有一定参考意义。

1 LCC-HVDC输电系统

LCC-HVDC系统的主电路及控制结构如图1所示。图1中：下标“r”表示整流侧相关变量；下标“i”表示逆变侧相关变量；Vs为交流电网的电压幅值；Rs和Ls分别为交流电网的等值电阻和等值电感；is为交流电网注入交流母线的电流；Vpcc为公共连接点电压；ic为流经换流变压器网侧的电流；k为换流变压器的变比；Lec为换流变压器对直流侧的等效 影 响电感［21］；Rdc1、Rdc2、Ldc1、Ldc2和Cdc分别为T型直流输电线路的等值电阻、电感和电容；Idc为直流电流；UCdc为直流输电线路中点对地电压；vr，d和vr，q分别为Vpccr的d轴和q轴分量；θ为PLL的输出相位；Idc，ref和Udc，ref分别为直流电流和直流电压的指令值；αord和βord为触发角指令值；αact和βact为实际触发角；F为交流滤波器组，其结构与参数与CIGRE标准测试模型［22］中交流滤波器组一致。

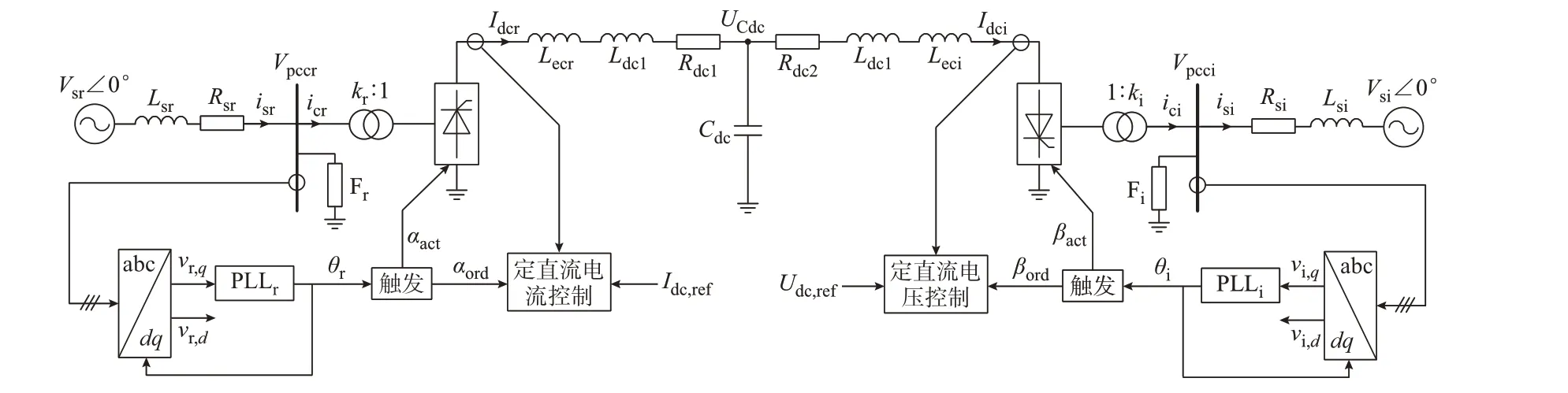
图1 LCC-HVDC系统主电路及控制结构Fig.1 Main circuit and control structure of LCC-HVDC system

2 系统线性化传递函数模型

2.1 时域线性化模型

根据图1可知，该系统结构可视为典型的MIMO系统，其输入为直流电流及直流电压指令值，输出为直流电流及直流电压测量值。现对系统主要环节的时域线性化模型进行说明，在时域线性化模型的基础上进行Laplace变换即可得到系统的线性化传递函数模型。

1）换流站模型。以整流侧为例，基于开关函数法，整流站网侧与直流侧电流间的关系可表示为：

式中：icr，d和icr，q分别为icr的d轴和q轴分量；μr为整流站换相重叠角；φr为整流站功率因数角；θactr为整流侧交流母线电压的实际相位。

μr、φr及θactr的计算公式为：

式中：XTr为整流侧换相电抗。

根据准稳态公式，整流站出口处的直流电压Udcr可表示为：

Vpccr的表达式为：

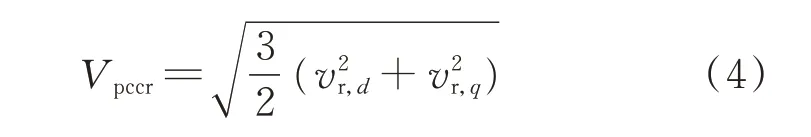
整流站的线性化模型可表示为：

式中：Δ表示扰动量，如Δicr，d代表icr，d的扰动量，其余类似；Ks1至Ks12的表达式详见附录A式（A1）。

2）定直流电流控制器模型。定直流电流控制器的原理框图见附录A图A1（a）。根据图A1（a）可推导其线性化模型为：

式中：p为微分算子；x1为中间状态变量；Idcr，m为直流电流测量值；TIdc和G1分别为电流测量环节的时间常数和比例系数；Kp，Idc和Ki，Idc分别为定电流控制器PI环节的比例系数和积分系数。

3）定直流电压控制器模型。定直流电压控制器的原理框图见附录A图A1（b）。根据图A1（b）可推导其线性化模型为：

式中：x2为中间状态变量；Udci，m为直流电压测量值；TUdc和G2分别为电压测量环节的时间常数和比例系数；Kp，Udc和Ki，Udc分 别 为 定 电 压 控 制 器PI环 节 的 比例系数和积分系数。

PLL、交流电网、交流滤波器及直流线路的时域线性化模型可参考文献［11］，文中不再赘述。

图1所示LCC-HVDC系统的时域线性化模型可表示为：

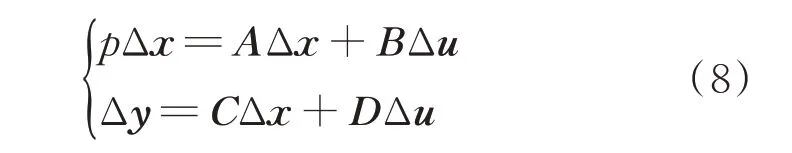
式 中：x为 状 态 变 量；u＝[Idc，ref，Udc，ref]T为 输 入 变量；y＝[Idcr，m，Udci，m]T为输出变量；A为39×39的状态 矩 阵；B为39×2的 输 入矩阵；C为2×39的 输 出矩阵；D为2×2的前馈矩阵。

2.2 线性化传递函数模型

在2.1节 中 建 立 了 以Idc，ref、Udc，ref为 输 入，Idcr，m、Udci，m为输出的系统时域线性化模型。式（8）经过Laplace变换可得系统的线性化传递函数模型为：

式中：I为单位矩阵；G11（s）、G12（s）、G21（s）和G22（s）均为传递函数。

为了验证上述传递函数模型的正确性，令系统初始时的运行及控制参数如附录A表A1和表A2所示，此时式（9）中各传递函数的单位阶跃响应见附录A图A2。在PSCAD中分别令Idc，ref和Udc，ref于t＝3 s时 由1.00 p.u.阶 跃 至0.95 p.u.，于t＝4 s时 由0.95 p.u.阶 跃 回1.00 p.u.。由 于PSCAD中Idc，ref和Udc，ref的阶跃变化量为0.05 p.u.，故将图A2中各传递函数的单位阶跃响应波形乘以系数0.05并与PSCAD相应波形进行比较，所得结果如附录A图A3所示。根据图A3可知，传递函数模型与PSCAD电磁暂态模型的动态响应波形相吻合，验证了本文所建立的传递函数模型的正确性。

根据式（9），LCC-HVDC系统的MIMO传递函数信号流图如图2（a）所示。当仅考虑一个输入扰动时，另一输入扰动可设为0，此时可将MIMO系统简化为SISO系统［15］，其信号流图如图2（b）所示。此时，信号流图中的传递函数G11（s）和G22（s）均为闭环传递函数，而使用经典控制理论中的GM、PM及灵敏度函数最大峰值指标对稳定性进行分析，是针对开环传递函数而言。因此，为便于后续分析说明，需要将图2（b）闭环传递函数形式下的SISO信号流图进一步等效转换为包含开环传递函数的单位负反馈形式，如图2（c）所示。图2（c）中，CIdc（s）和CUdc（s）分别为定直流电流控制回路和定直流电压控制回路在单位负反馈形式下的开环传递函数。则根据图2（b）及图2（c）有：

图2 LCC-HVDC传递函数信号流图Fig.2 Signal flow graph of LCC-HVDC transfer function

联立式（10）及式（11）可得：

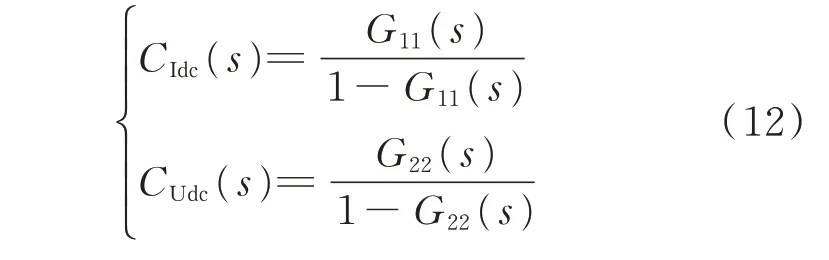
基于式（12）应用经典控制理论即可对LCCHVDC系统直流控制回路的稳定性进行分析。

2.3 SISO模型与MIMO模型一致性说明

为便于说明，现基于状态空间模型的Laplace变换建立以Δαord、Δβord为输入，ΔIdcr，m、ΔUdci，m为输出的线性化传递函数模型，有

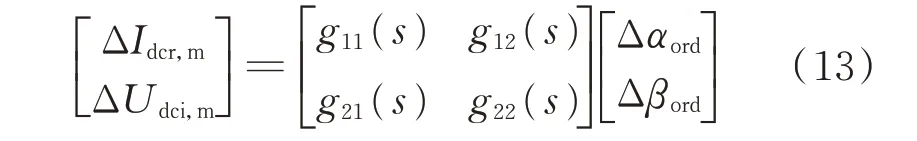
式中：g11（s）、g12（s）、g21（s）和g22（s）均为传递函数。

则图2（a）所示MIMO信号流图可等效表示为附录A图A4。在图A4中，gIdc（s）和gUdc（s）分别为定电流及定电压控制器PI环节的传递函数。

以定直流电流控制回路的传递函数建模为例，将ΔUdc，ref视为扰动量并设为0，此时根据图A4有：

由式（14）可得：

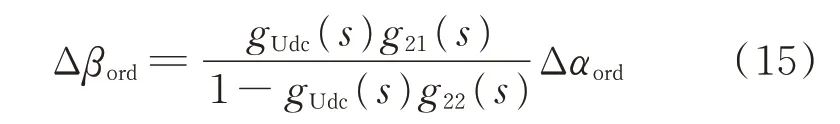
又因为：

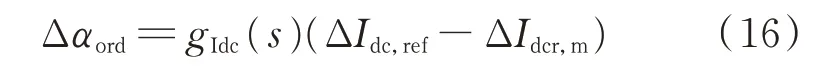
则根据图A4有：

定义GIdc（s）为定直流电流控制回路的闭环传递函数，由式（17）可得：

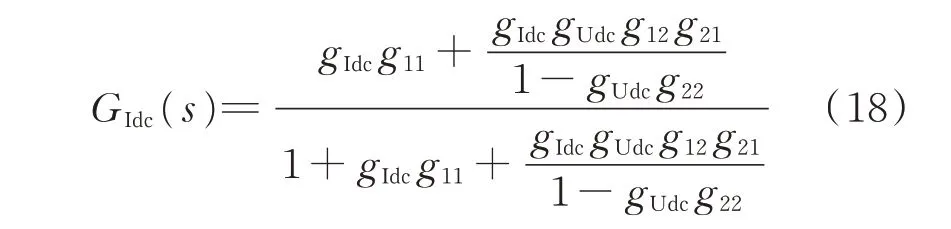
为使公式更加简洁，式（17）及式（18）中各传递函数的“（s）”符号均省略。

令系统运行于附录A表A1及表A2所示参数下，此时传递函数G11（s）与GIdc（s）的波特图如附录A图A5所示。根据图A5可知，二者的波特图一致，说明G11（s）与GIdc（s）等价。从图A4及上述推导过程来看，G11（s）中已包含直流电压与直流电流间的耦合关系。将控制器指令值的扰动量设置为0不会改变MIMO系统的内部结构。因此，本文采用的SISO简化模型仍包含原MIMO系统的结构信息，其稳定特征与原MIMO系统一致，能够准确地描述系统的稳定特性。基于SISO模型得出的理论分析结果将仍适用于MIMO系统。

3 直流控制回路小干扰稳定性分析

2.2节中得到了直流控制回路的开环传递函数CIdc（s）和CUdc（s），本章将在CIdc（s）和CUdc（s）的基础上，采用GM、PM和灵敏度函数最大峰值指标，定量评估直流控制回路带宽、逆变侧PLL带宽和逆变侧交流电网强度对各直流控制回路小干扰稳定性的影响。

3.1 评估指标及稳定判据

在分析直流控制回路的小干扰稳定性前，首先给出各评估指标及稳定判据的说明。其中，GM的物理意义为：对于闭环稳定系统，如果系统开环幅频特性再增大GM值对应的倍数，则系统将变为临界稳定状态。PM的物理意义为：对于闭环稳定系统，如果开环相频特性再滞后PM值对应的角度，则系统将变为临界稳定状态［23］。灵敏度函数为系统闭环传递函数的变化率与被控过程传递函数变化率的比值，本文灵敏度函数最大峰值指标Ms定义为：

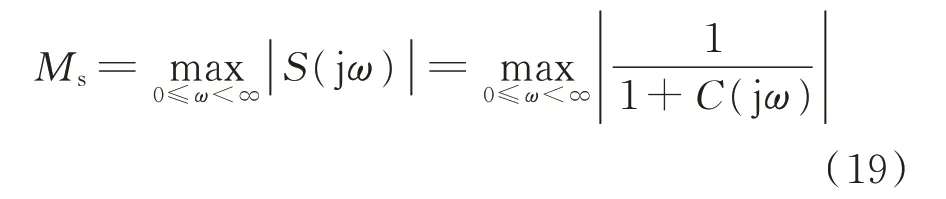
式中：S（jω）为控制回路的灵敏度函数；C（jω）为被控过程的传递函数，对于定直流电流控制回路有C(jω)＝CIdc(jω)，对 于 定 直 流 电 压 控 制 回 路 有C(jω)＝CUdc(jω)。式（19）的推导过程详见附录B。

当灵敏度函数最大峰值较小时，则在所有频率上S（jω）的幅值都小，干扰被一致衰减；而当灵敏度函数最大峰值较大时，则在部分频率上干扰衰减的效果较弱，反馈控制系统对扰动较敏感，系统鲁棒性减弱。因此，Ms可以用来定量评估控制系统的鲁棒性。

值得注意的是，在弱短路比下CIdc（s）和CUdc（s）均具有RHP零点，如附录C图C1所示。则此时系统为非最小相位系统，经典控制理论中的PM稳定判据应根据零极点分布做出相应修正［15］。因此，下述直流控制回路稳定性分析将以Nyquist稳定判据为主，以波特图作辅助说明。其中，对Nyquist稳定判据的具体表述为：当且仅当开环传递函数RHP极点数P与Nyquist曲线逆时针包围点(－1，j0)的周数N相等时，有闭环传递函数RHP极点数Z＝P－N＝0，此时系统是闭环稳定的，否则系统失稳。

3.2 定直流电流控制回路稳定性分析

首先考虑定直流电流控制回路自身带宽ωIctrl对定直流电流控制回路稳定性的影响。由于CIdc（s）具有RHP零点，故根据经典控制理论可以预见定直流电流控制回路带宽受限［24］，即高带宽下控制回路易失 稳。具体地，取ωIctrl分别为11.31、13.11、14.29、15.36 Hz，得到CIdc（s）的Nyquist图如图3（a）所示。ωIctrl为11.31、13.11、14.29 Hz时，CIdc（s）均无正极点，P＝0，在图3（a）中相应的Nyquist曲线均不包围点(－1，j0)，N＝0，Z＝P－N＝0，此时定直流电流控制回路始终保持稳定。而当ωIctrl＝15.36 Hz时，CIdc（s）无正极点，P＝0，Nyquist曲线顺时针包围点(－1，j0)2周，N＝－2，Z＝P－N＝2，此时定直流电流控制回路闭环失稳。对应CIdc（s）的波特图如附录C图C2（a）所示，随着ωIctrl的逐渐增大，CIdc（s）的波特图幅频特性上移，对应相频特性穿越频率处的幅值逐渐靠近并穿过0 dB线，幅频特性剪切频率处对应的相位逐渐靠近并穿过180°线。不同ωIctrl下定直流电流控制性能评估指标的具体数值如表1所示。

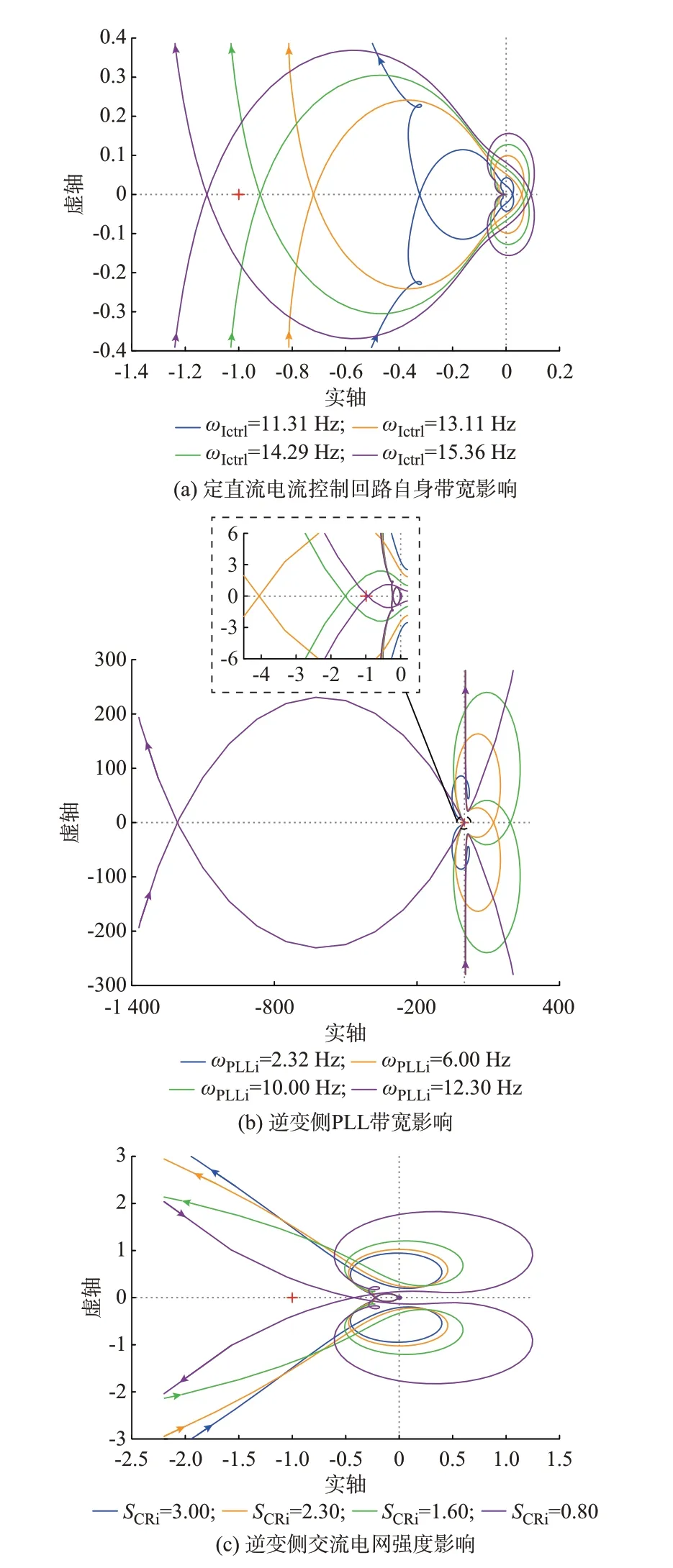
图3 CIdc(s)的Nyquist图Fig.3 Nyquist diagram of CIdc(s)

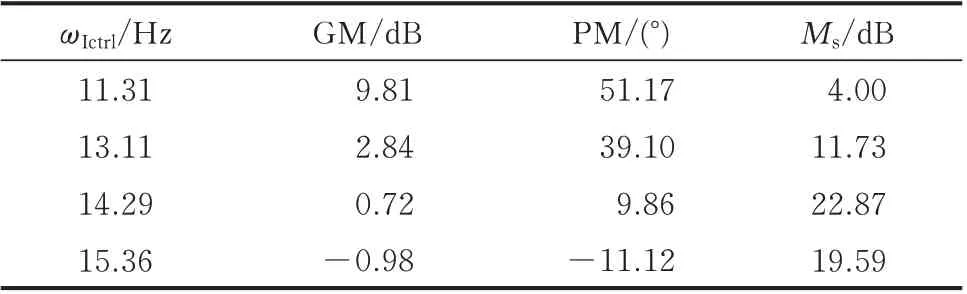
表1 不同ωIctrl下定直流电流控制性能评估指标Table 1 Evaluation indices of constant DC current control performance with different ωIctrl

由表1可知，增大ωIctrl会使定直流电流控制回路的GM、PM指标均明显降低，同时Ms显著增大。随着ωIctrl的增大，定直流电流控制回路的小干扰稳定性和鲁棒性均明显减弱，过高的ωIctrl将使得定直流电流控制回路由于GM和PM均不足而闭环失稳。进一步测得ωIctrl致使定直流电流控制回路闭环 失 稳 的 临 界 值 为14.73 Hz，则 在ωIctrl＜14.73 Hz范 围 内 通 过 减 小Kp，Idc从 而 适 当 减 小ωIctrl，有利于扩大定直流电流控制回路的GM及PM。

考虑逆变侧PLL带宽ωPLLi对定直流电流控制回 路 稳 定 性 的 影 响，取ωPLLi分 别 为2.32、6.00、10.00、12.30 Hz，得到CIdc（s）的Nyquist图如图3（b）所示。ωPLLi＝2.32 Hz时，CIdc（s）无正极点，P＝0，Nyquist曲 线 不 包 围 点(－1，j0)，N＝0，Z＝PN＝0，定 直 流 电 流 控 制 回 路 稳 定；ωPLLi为6.00、10.00 Hz时，CIdc（s）有2个正极点，P＝2，Nyquist曲线逆时针包围点(－1，j0)2周，N＝2，Z＝P－N＝0，定直流电流控制回路稳定；ωPLLi＝12.30 Hz时，CIdc（s）无正极点，P＝0，Nyquist曲线顺时针包围点(－1，j0)2周，N＝－2，Z＝P－N＝2，定直流电流控制回路闭环失稳。对应CIdc（s）的波特图如附录C图C2（b）所示，随着ωPLLi逐渐增大，CIdc（s）的波特图相频特性穿越频率处的幅值不发生明显变化，但幅频特性剪切频率处对应的相位逐渐靠近180°线。不同ωPLLi下定直流电流控制带宽及其性能评估指标的具体数值如表2所示。

表2 不同ωPLLi下定直流电流控制性能评估指标Table 2 Evaluation indices of constant DC current control performance with different ωPLLi

由表2可知，增大ωPLLi会使得定直流电流控制回路的PM指标显著降低，同时Ms显著增大。随着ωPLLi的增大，定直流电流控制回路的小干扰稳定性和鲁棒性均明显减弱，过高的ωPLLi将使得定直流电流控制回路由于PM不足而闭环失稳。进一步测得ωPLLi致使定直流电流控制回路闭环失稳的临界值为11.47 Hz，则在ωPLLi＜11.47 Hz范围内通过减小逆变侧PLL的PI环节比例及积分系数来适当减小ωPLLi，有利于扩大定直流电流控制回路的PM。

考虑逆变侧交流电网强度SCRi对定直流电流控制回路稳定性的影响，取SCRi分别为3.0、2.3、1.6、0.8，得 到CIdc（s）的Nyquist图 如 图3（c）所 示。当SCRi为3.0、2.3、1.6时，CIdc（s）均无正极点，P＝0，在图3（c）中相应的Nyquist曲线均不包围点(－1，j0)，N＝0，Z＝P－N＝0，故此时定 直流电流控制回路始终保持稳定；当SCRi＝0.8时，CIdc（s）有2个 正 极 点，P＝2，Nyquist曲 线 不 包 围 点(－1，j0)，N＝0，Z＝P－N＝2，定直流电流控制回路闭环失稳。对应CIdc（s）的波特图如附录C图C2（c）所示，在定直流电流控制回路闭环稳定的前提下，随着SCRi的逐渐减小，CIdc（s）的波特图幅频特性和相频特性均无明显变化。不同SCRi下定直流电流控制性能评估指标的具体数值如表3所示。

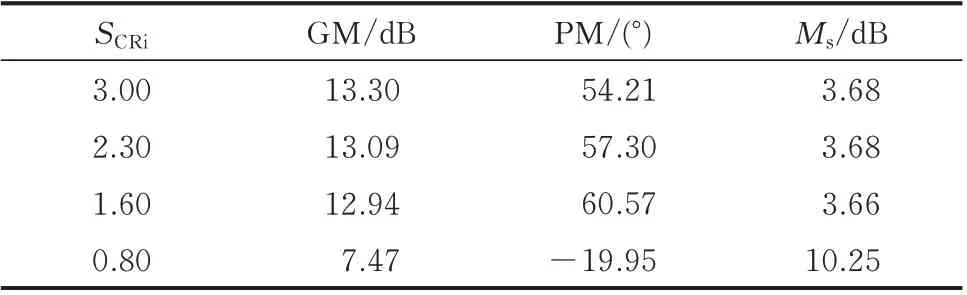
表3 不同SCRi下定直流电流控制性能评估指标Table 3 Evaluation indices of constant DC current control performance with different SCRi

由表3可知，在定直流电流控制回路闭环稳定的前提下，减小SCRi时定直流电流控制回路的GM、PM及Ms的变化均不明显，故逆变侧交流电网的强弱并不影响定直流电流控制回路的小干扰稳定性和鲁棒性。

3.3 定直流电压控制回路稳定性分析

首先，考虑定直流电压控制回路自身带宽ωUctrl对定直流电压控制回路稳定性的影响。由于CUdc（s）也具有RHP零点，故根据经典控制理论可以预见定直流电压控制回路带宽亦受限。具体地，取ωUctrl分 别 为8.90、14.77、49.25、188.06 Hz，得 到CUdc（s）的Nyquist图如图4（a）所示。ωUctrl为8.90、14.77、49.25 Hz时，CUdc（s）均无正极点，P＝0，在图4（a）中Nyquist曲 线 均 不 包 围 点(－1，j0)，N＝0，Z＝P－N＝0，故此时定直流电压控制回路始终保持稳定；ωUctrl＝188.06 Hz时，CIdc（s）无正极点，P＝0，Nyquist曲线顺时针包围点(－1，j0)2周，N＝－2，Z＝P－N＝2，定直流电压控制回路闭环失稳。对应CUdc(s)的波特图如附录C图C3（a）所示，随着ωUctrl的逐渐增大，CUdc（s）的波特图幅频特性上移，对应相频特性穿越频率处的幅值逐渐靠近0 dB线，幅频特性剪切频率处对应的相位逐渐靠近180°线。不同ωUctrl下定直流电压控制性能评估指标的具体数值如表4所示。

图4 CUdc(s)的Nyquist图Fig.4 Nyquist diagram of CUdc(s)

由表4可知，增大ωUctrl会使得定直流电压控制回路的GM、PM指标均明显降低，同时Ms显著增大。随着ωUctrl的增大，定直流电压控制回路的小干扰稳定性和鲁棒性均明显减弱，过高的ωUctrl将使得定直流电压控制回路由于GM和PM均不足而闭环失稳。进一步测得ωUctrl致使定直流电压控制回路闭环失稳的临界值为50.30 Hz，则在ωUctrl＜50.30 Hz范围内通过减小Kp，Udc从而适当减小ωUctrl，有利于扩大定直流电压控制回路的GM及PM。

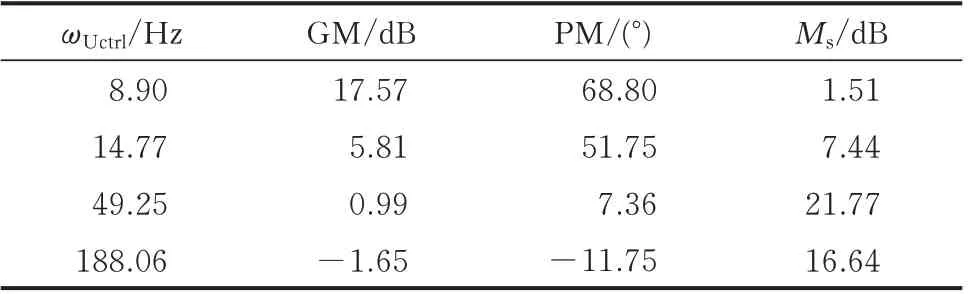
表4 不同ωUctrl下定直流电压控制性能评估指标Table 4 Evaluation indices of constant DC voltage control performance with different ωUctrl

考虑逆变侧PLL带宽ωPLLi对定直流电压控制回 路 稳 定 性 的 影 响，取ωPLLi分 别 为2.32、6.00、10.00、12.30 Hz，得到CUdc（s）的Nyquist图如图4（b）所 示。ωPLLi为2.32、6.00 Hz时，CUdc（s）无正极点，P＝0，Nyquist曲 线 不 包 围 点(－1，j0)，N＝0，Z＝P－N＝0，定直流电压控制稳定；ωPLLi＝10.00 Hz时，CUdc（s）有2个正极点，P＝2，Nyquist曲线逆时针包 围点(－1，j0)2周，N＝2，Z＝P－N＝0，定 直流电压控制稳定；ωPLLi＝12.30 Hz时，CUdc（s）有2个正极点，P＝2，Nyquist曲线不包围点(－1，j0)，N＝0，Z＝P－N＝2，定直流电压控制不稳定。对应的CUdc（s）波特图如附录C图C3（b）所示，随着ωPLLi逐渐增大，CUdc（s）的波特图相频特性穿越频率处的幅值不发生明显变化，但幅频特性剪切频率处对应的相位逐渐靠近180°线。不同ωPLLi下定直流电压控制带宽及其性能评估指标的具体数值如表5所示。

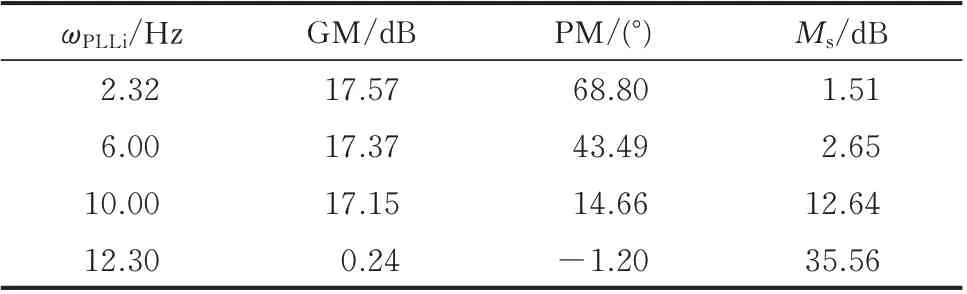
表5 不同ωPLLi下定直流电压控制性能评估指标Table 5 Evaluation indices of constant DC voltage control performance with different ωPLLi

由表5可知，增大ωPLLi会使得定直流电压控制回路的PM指标显著降低，同时Ms显著增大。随着ωPLLi的增大，定直流电压控制回路的小干扰稳定性和鲁棒性均明显减弱，过高的ωPLLi将使得定直流电压控制回路由于PM不足而闭环失稳。进一步测得ωPLLi致使定直流电压控制回路闭环失稳的临界值亦为11.47 Hz，则在ωPLLi＜11.47 Hz范围内通过减小逆变侧PLL的PI环节比例及积分系数来适当减小ωPLLi，有利于扩大定直流电压控制回路的PM。

考虑逆变侧交流电网强度SCRi对定直流电压控制回路稳定性的影响，取SCRi分别为3.0、2.3、1.6、0.8，得到CUdc（s）的Nyquist图如图4（c）所示。当SCRi为3.0、2.3、1.6时，CUdc（s）均无正极点，P＝0，在图4（c）中 相 应Nyquist曲 线 均 不 包 围 点(－1，j0)，N＝0，Z＝P－N＝0，故此时定直流电压控制回路始终保持稳定；当SCRi＝0.8时，CUdc（s）有2个正极点，P＝2，Nyquist曲 线 不 包 围 点(－1，j0)，N＝0，Z＝P－N＝2，定直流电压控制回路闭环失稳。对应的CUdc（s）波特图如附录C图C3（c）所示，随着SCRi的逐渐减小，CUdc（s）的波特图相频特性穿越频率处的幅值逐渐靠近0 dB线，幅频特性剪切频率处对应的相位逐渐靠近180°线。不同SCRi下定直流电压控制性能评估指标的具体数值如表6所示。

表6 不同SCRi下定直流电压控制性能评估指标Table 6 Evaluation indices of constant DC voltage control performance with different SCRi

由表6可知，减小SCRi会使得定直流电压控制回路的GM、PM指标有所降低，定直流电压控制回路的小干扰稳定性有所减弱，过低的SCRi将使得定直流电压控制回路由于GM和PM不足而闭环失稳。

4 仿真验证

为验证上述分析结果的正确性，在PSCAD电磁暂态模型中分别采用控制器指令值发生阶跃及交流母线处发生接地故障的方式，观察不同影响因素下Idcr，m及Udci，m的波形变化情况。系统初始时运行于附录A表A1及表A2所示的参数下。

1）定直流电流控制回路稳定性分析验证

首先，观察定直流电流控制器指令值发生阶跃时直流电流测量值的响应波形。在t＝4 s时，令Idc，ref产生扰动，扰动量ΔIdc，ref＝－0.05 p.u.。在定直流电流控制回路闭环稳定的前提下分别取ωIctrl、ωPLLi及SCRi如表1至表3所示参数，得到Idcr，m的仿真响应波形分别如图5（a）至图5（c）所示。

根据图5（a）至图5（c）可知，当ωIctrl和ωPLLi逐渐增大时，Idcr，m受扰波形的振荡幅度逐渐增大，定直流电流控制回路的阻尼特性变差，小干扰稳定性逐渐减 弱；而 当SCRi逐 渐 减 小 时，Idcr，m受 扰 波 形 无 明 显 区别，则SCRi对定直流电流控制回路的阻尼特性及小干扰稳定性不产生明显影响。

为进一步验证定直流电流控制回路稳定性的理论分析结果，在PSCAD电磁暂态模型中设置整流侧交流母线于t＝4 s时发生三相接地故障，过渡电阻为200 Ω，故障持续时间为0.1 s，同样在定直流电流控制回路闭环稳定的前提下分别取ωIctrl、ωPLLi及SCRi如表1至表3所示参数，得到Idcr，m的仿真响应波形分别如图5（d）至图5（f）所示。

根据图5（d）至图5（f）可知，当ωIctrl和ωPLLi逐渐增大时，故障切除后Idcr，m响应波形的振荡幅度增大，振荡频率增高，说明定直流电流控制回路的阻尼减弱，小干扰稳定性减弱；而当SCRi逐渐减小时，故障期间及故障恢复过程中Idcr，m响应波形无明显区别，则SCRi对定直流电流控制回路的阻尼特性及小干扰稳定性不产生明显影响，仿真结果与3.2节分析结果一致，验证了理论分析结果的正确性。

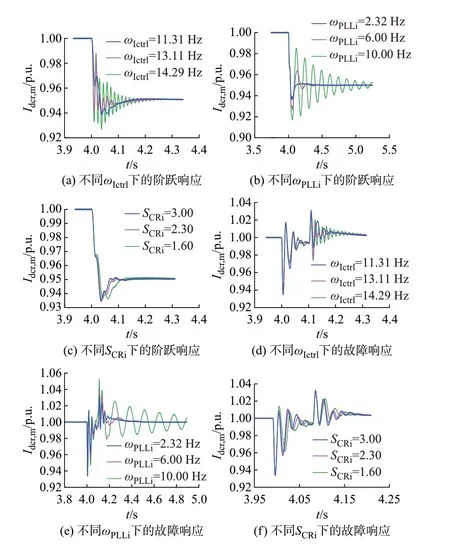
图5 不同影响因素下Idcr,m的响应波形Fig.5 Response waveforms of Idcr,m with different influencing factors

2）定直流电压控制回路稳定性分析验证

首先，观察定直流电压控制器指令值发生阶跃时直流电压测量值的响应波形。在t＝4 s时，令Udc，ref产 生 扰 动，扰 动 量ΔUdc，ref＝－0.05 p.u.。在 定直流电压控制回路闭环稳定的前提下分别取ωUctrl、ωPLLi及SCRi如表4至表6所示参数，得到Udci，m的仿真响应波形分别如附录D图D1（a）至图D1（c）所示。需要指出的是，由于SCRi对定直流电压控制回路的GM、PM及Ms影响程度不如其他参数大，为使仿真结果更加明晰，在更改SCRi进行仿真验证时，系统首先 运行于Kp，Udc＝4的情况下。

根据图D1（a）至图D1（c）可知，当ωUctrl和ωPLLi逐渐增大、SCRi逐渐减小时，Udci，m受扰波形的振荡幅度逐渐增大，定直流电压控制回路的阻尼特性变差，小干扰稳定性逐渐减弱。

为进一步验证定直流电压控制回路稳定性的理论分析结果，在PSCAD电磁暂态模型中设置整流侧交流母线于t＝4 s时发生三相接地故障，过渡电阻为200 Ω，故障持续时间为0.1 s，同样在定直流电压控制回路闭环稳定的前提下分别取ωUctrl、ωPLLi及SCRi如表4至表6所示参数，得到Udci，m的仿真响应波形分别如图D1（d）至图D1（f）所示。

根据图D1（d）至图D1（f）可知，当ωUctrl和ωPLLi逐渐增大、SCRi逐渐减小时，故障切除后Udci，m响应波形的振荡幅度逐渐增大，说明定直流电压控制回路的阻尼减弱，小干扰稳定性减弱，仿真结果与3.3节分析结果一致，验证了理论分析结果的正确性。

对系统不加以扰动，仅在t＝3 s时分别令ωIctrl由11.31 Hz阶跃至15.36 Hz、ωUctrl由8.90 Hz阶跃至188.06 Hz、ωPLLi由2.32 Hz阶 跃 至12.30 Hz、SCRi由1.60斜坡下降至0.80，得 到Idcr，m及Udci，m的 仿 真 波 形如附录D图D2所示。根据图D2可知，当系统运行于上述参数下时系统无法保持稳定，与3.2及3.3节分析结果一致，验证了理论分析结果的正确性。

5 结语

本文推导建立了LCC-HVDC系统直流控制回路的线性化传递函数模型，基于经典控制理论采用GM、PM和灵敏度函数最大峰值指标，定量评估了直流控制回路带宽、逆变侧PLL带宽和逆变侧交流电网强度对直流控制回路稳定性的影响，得到如下结论。

1）弱交流电网条件下LCC-HVDC直流控制回路的开环传递函数存在RHP零点，控制回路自身带宽受限，高带宽易导致GM和PM不足，严重影响控制回路的稳定性；适当降低控制回路自身带宽，有利于提高控制回路的GM和PM，进而提高系统稳定性。

2）逆变侧PLL带宽会同时影响定直流电流及定直流电压控制回路的稳定性，高逆变侧PLL带宽易导致PM不足，进而使得直流控制回路闭环失稳；适当降低逆变侧PLL带宽有利于提高直流控制回路的PM，进而提高系统稳定性。

3）逆变侧交流电网强度主要影响定直流电压控制回路的稳定性，而对定直流电流控制回路的稳定性无明显影响；增大逆变侧交流电网强度有利于提高定直流电压控制回路的稳定性。

本文重点研究了额定运行工况下系统参数对LCC-HVDC系统直流控制回路小干扰稳定性的影响，非额定运行工况下的影响规律有待进一步探究。