基于ADAMS的高精度光纤张力传感器仿真设计*
罗 声,程志远,李维嘉,单福林
(1. 西安工程大学机电工程学院,陕西 西安 710048;2. 华中科技大学船舶与海洋工程学院,湖北 武汉 430074;3. 九江四元科技有限公司,江西 九江 332000)
引 言
在光纤绕制过程中,对张力的精确测量和高精度控制是保证光纤环品质的重要环节。光纤张力传感器是测量光纤内部张力的测量元件,属于动态张力测量范畴。纤细的光纤非常脆弱,绕制过程中的张力值仅有0.1~0.2 N。对于高性能的光纤环,要求绕制过程中的张力精度控制范围不超过0.002 N,这就要求张力传感器的测量精度不得低于0.001 N。同时,在绕制过程中,光纤的高频振颤也会给张力的测量带来干扰信号,这就给高精度、高敏感的光纤张力传感器的研制提出了非常高的要求[1]。针对现有的多采用应变式测量和位移传感器测量的光纤张力传感器[2],本文提出了一种基于摆角测量的浮动式光纤张力的测量方法,利用ADAMS仿真平台构建了浮动式张力测量元件的动力学模型,开展了结构参数的优化匹配,确定了合适的设计参数。样机的试验结果达到了0.001 N的检测精度,并在光纤绕制机上得到了应用。
1 动态张力测量方式
常用的动态张力测量方式有2种:应变式张力测量方式和浮动式张力测量方式,如图1所示。采用应变片检测张力是一种直接测量张力的方式,通常需要应变片或压力传感器与导线轮组合,结构类型比较多样[3-4]。应变片式测量结构由2个对称布置的定滑轮负责导线,光纤的张力T与应变片测得的压力N和测力轮、导向轮之间的夹角θ存在着N= 2Tcosθ的关系式,可以认为θ在工作过程中保持不变,测出压力就可以得到张力。这种测量方式的优点是响应灵敏,测量精度高,价格便宜。缺点是缺少储能原件,无法吸收张力突变时的张力峰值,当有外部扰动时,张力值变化过大,容易引起控制系统的震荡,不利于控制系统的稳定。
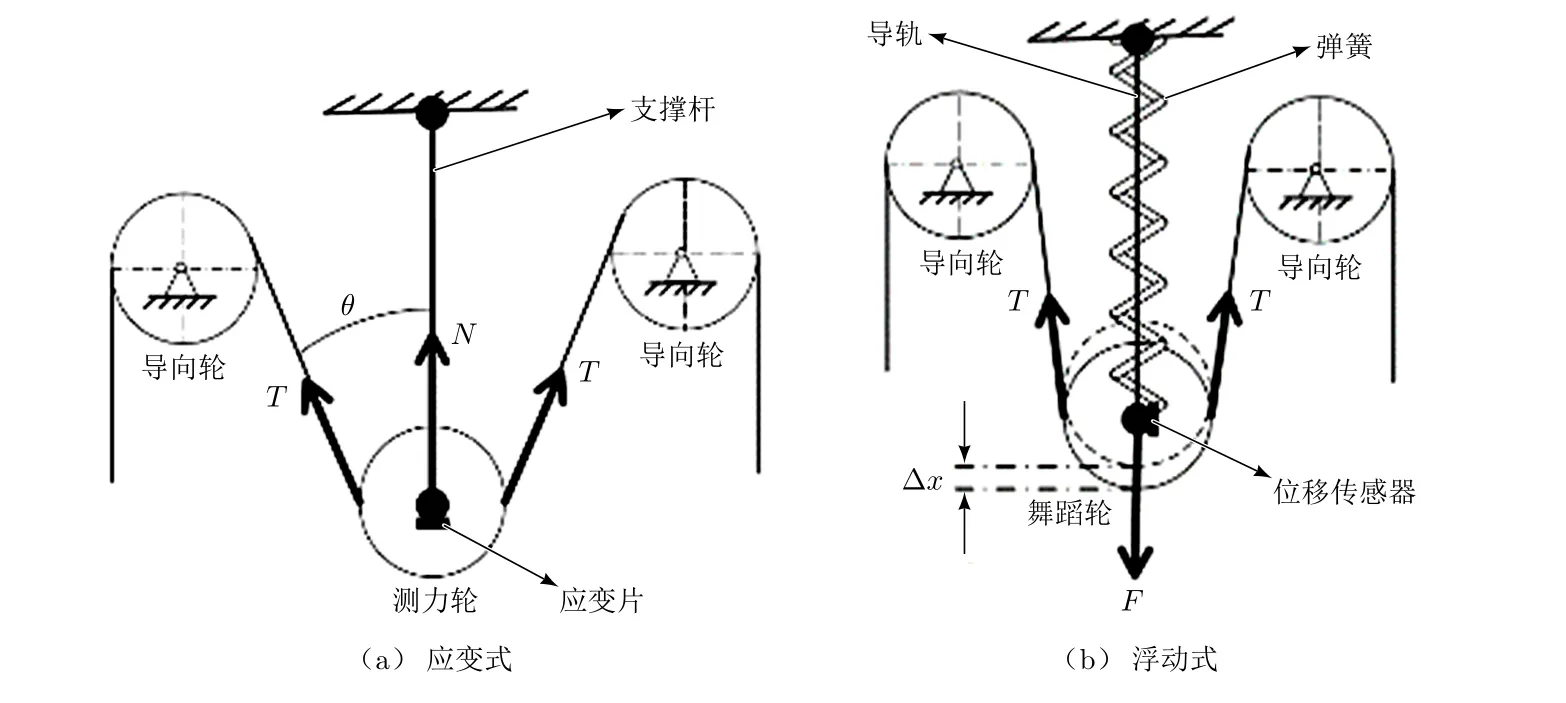
图1 典型张力测量方式
浮动式张力测量是一种间接张力测量方式,张力大小由测量机构的位移或角度反映出来,通过位移或角度传感器间接得到[5]。当张力T稳定时,舞蹈轮的弹簧力F与张力保持在某个稳定的平衡位置。当张力发生变化时,通过位移传感器可以得到舞蹈轮的位移变化值Δx,并得出张力的对应值。该测量方法包含储能设备,可以吸收大干扰引起的张力波动,保证了系统的稳定性。其缺点是设计较为复杂,主要体现在需要对弹簧的参数和3个轮子的相对位置进行优化匹配,以满足高精度的动态测量要求。另外,为了实现微小量的测量,现有的方法是采用高精度、高敏感、低惯量的位移传感器,价格较为昂贵。
针对浮动式张力测量传感器在使用位移传感器实现张力测量时存在的不足,本文采用角度传感器,在同样的张力情况下,传感器的摆动角度更大,而且采用滚动轴承可进一步减小测量机构的静摩擦和动摩擦,从而提高测量的灵敏度。
2 仿真分析及参数优化匹配
2.1 张力传感器的建模
基于角度传感器的光纤张力测量系统的结构如图2所示。由放线轮引出的光纤依次经过定滑轮、舞蹈轮、定滑轮,然后绕制到光纤环上。舞蹈轮基座通过连杆与角度传感器相连的同时还与一端固定的弹簧相连。在稳定状态下,舞蹈轮在光纤张力T,连杆支撑力N和弹簧弹力F的共同作用下保持平衡,其受力分析如图2所示。

图2 张力传感器结构(改进后)
角度传感器可以测出连杆相对于参考位置的角度θ。当光纤张力发生变化时,舞蹈轮与连杆发生摆动,角度传感器可以测出摆动的角度大小,通过测量角度就可以得到张力的大小。
在ADAMS中建立的光纤张力测量系统的动力学模型如图3所示。3个滑轮、连杆、舞蹈轮之间的相对位置固定,通过调整密度来调整各个元件的质量。用绳索模型模拟光纤,出于仿真的需要,光纤模型一端固定,另一端与沿x轴方向的力相连。
2.2 张力测量传感器的指标要求
在光纤环的绕制过程中,光纤在光纤环上每缠绕一周,其线速度可以分为2个阶段:保持速度大小不变的匀速阶段和先加速后减速的变速阶段。由胡克定律可知,光纤线速度的变化会引起张力值的变化,变速阶段的存在相当于对光纤张力产生周期性的扰动,扰动的频率与收线轮转速有关,每转会产生一个扰动。
光纤环绕制设备的最大工作速度是60 r/min,因此光纤张力周期性变化的最大频率是1 Hz。此外,在绕制过程中张力的控制精度应满足±0.001 N的要求。
根据以上情况,对张力传感器的设计提出以下要求:
1)系统频宽为1.5 Hz;
2)测量范围为0.10~0.25 N;
3)测量精度为0.001 N;
4)灵敏度为0.000 5 N。
2.3 张力测量系统结构参数的优化匹配
弹簧是张力传感器中影响响应输出的重要元器件,因此,选择一组合适的弹簧参数是仿真的重要环节。可以通过试错的方法,选一个合适的区间,在该区间内选取不同的参数进行仿真测试,最终确定合适的弹簧参数。
根据建立的仿真模型(图3),只改变弹簧的质量、刚度和阻尼,用同样的外力作为输入,观测连杆摆动角度的变化,得到由扰动引起的张力传感器的输出值。为了模拟张力波动的频率,仿真时外力成分包含阶跃信号和一个频率为1.5 Hz的正弦扰动。正弦信号δ=0.004 9 sin(3πt),其中,0.004 9为0.5 g质量的重力,N;t为响应时间,s。经过仿真,得到4组不同参数下由扰动引起的输出值,见表1。
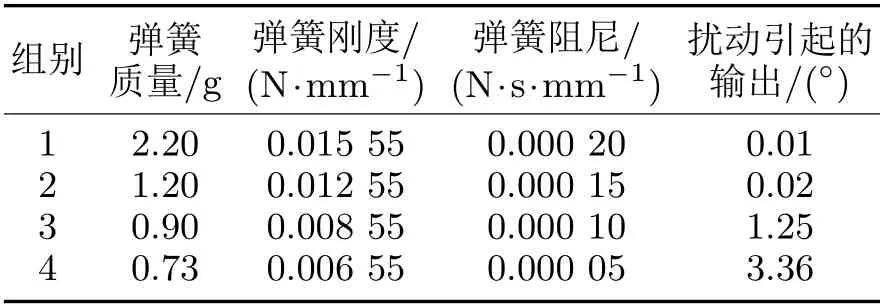
表1 不同参数仿真效果对比
角度传感器的最小分辨率为0.015°,考虑到环境的影响,张力传感器的输出值应具有一定的冗余。
第1组由扰动引起的输出值为0.01°,角度传感器无法测出;第2组的输出值虽然大于0.015°,但比较接近0.015°,容易受到环境温度、湿度等的影响,冗余不够,也不合适;第4组的输出值过大,当张力变化大时,张力传感器容易震荡,甚至发散,稳定性差;第3组的参数比较合适,既能保证测出因扰动引起的张力变化,也不会发生振荡。因此,第3组参数是仿真得到的最理想的弹簧参数。在弹簧预紧力为-0.007 N、连杆长30 mm、连杆铰链静摩擦系数为0.14、连杆铰链动摩擦系数为0.093这组参数下,张力传感器可以测出频率为1.5 Hz、幅值为0.004 9 N的扰动信号,其时间响应曲线如图4所示。

图4 张力传感器模型在1.5 Hz扰动信号下的响应曲线
3 试验验证
根据仿真获得的优化匹配参数,开展了样机的研发工作,选配合适的器件制造出了如图5所示的张力传感器。

图5 张力传感器实物
3.1 张力传感器的标定
角度传感器的型号为MCJSV010A-30-38AH,该传感器的测量精度高,可以满足张力传感器的测力需求,其关键参数为量程0°~30°,电源DC 24 V,输出电压0~10 V,精度0.05%。
为了得到张力与传感器输出值之间的数学关系,需要进行张力传感器的标定,采用吊挂质量的方法进行标定试验。
记录的试验数据见表2,绘制出质量与张力传感器输出电压之间的曲线,如图6所示。
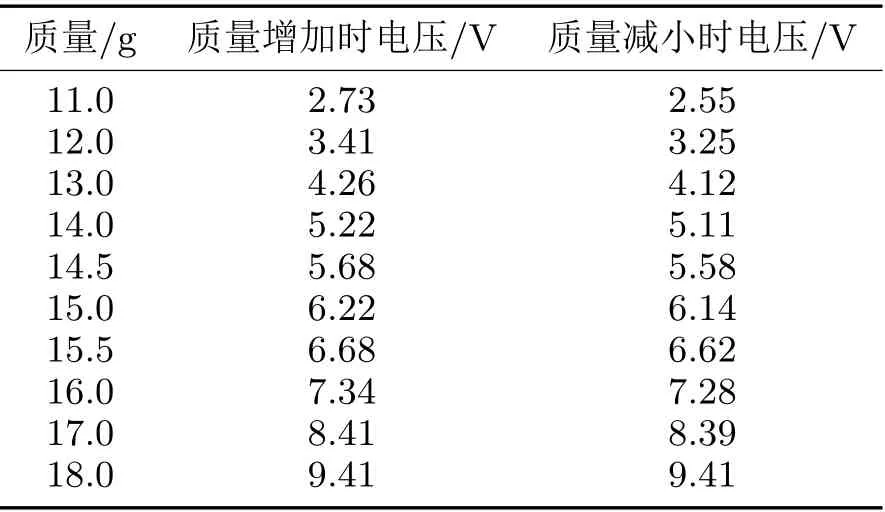
表2 张力传感器标定数据表
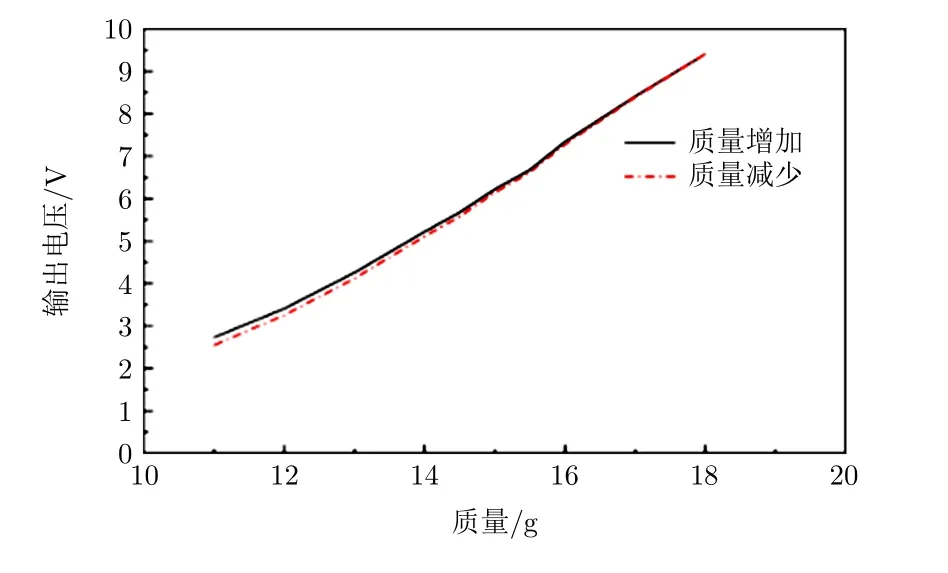
图6 张力传感器输入输出拟合曲线
根据表2中的数据拟合出二者之间的数学关系式:

式中:u为输出电压,V;m为质量,g。
张力传感器的测量精度约为0.000 8 N,满足测量要求。
3.2 阶跃响应试验
在光纤的一端加入15 g的阶跃力,用示波器测出的阶跃响应曲线如图7的实线所示,虚线则是由仿真模型得到的响应曲线。
从图7可以看出,试验与仿真数据基本一致。说明在ADAMS中建立的模型准确,与实物契合度高,在仿真中优化匹配的弹簧参数较为合理,可以用来指导高精度张力传感器的研制工作。
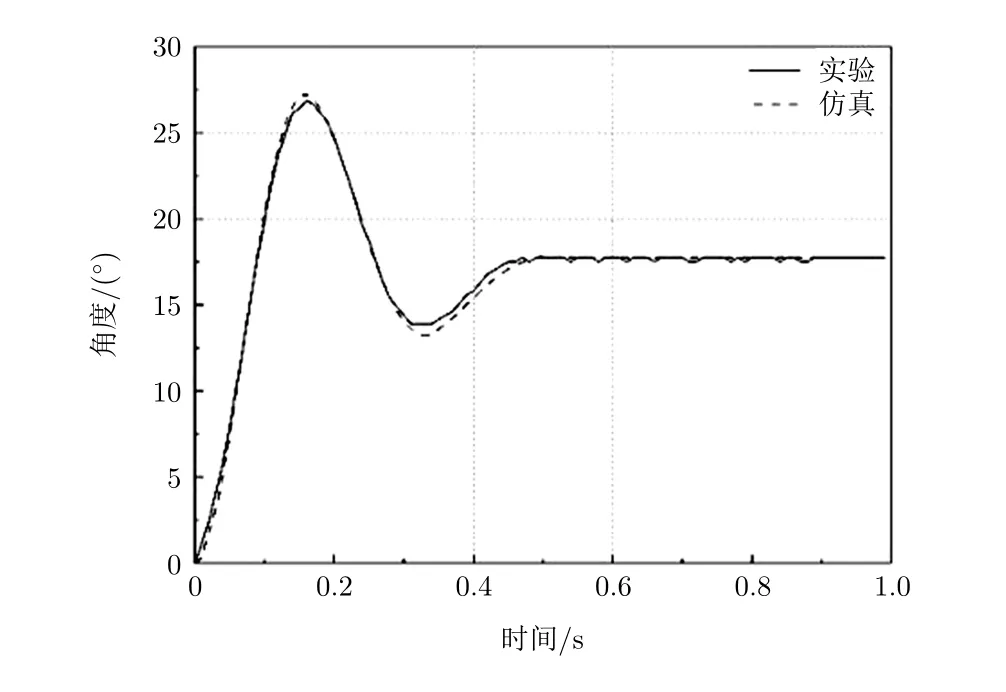
图7 张力传感器仿真与试验对比图
4 结束语
本文针对高精度光纤张力测控系统中张力传感器的研发工作需要,利用ADAMS仿真开展了张力传感器的弹簧质量、刚度、阻尼等关键参数的优化匹配,研制出了张力传感器样机,并对样机进行了测试。
实物的测试数据表明,张力传感器的测量精度高达0.000 8 N,系统频宽大于1.5 Hz,满足高精度光纤张力测控系统的测量要求。在ADAMS中建立的张力传感器模型准确度高,仿真设计的方法效率高,可以在光纤张力测量领域发挥作用。

