基于联合仿真方法的铁路钢桁梁桥局部应力分析
朱志辉,陈 伟,龚 威,张 磊,胡 狄,贺学军
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075)
铁路简支钢桁梁桥因具有跨度大、自重轻、受力明确、施工周期短等优点而被广泛使用[1]。由于钢桁梁桥节点板处汇交杆件较多,构造及受力复杂,焊缝密集,列车荷载引起的疲劳问题突出,因此为准确评估桥梁疲劳寿命,有必要对钢桁梁桥节点板进行局部应力分析[2]。以往许多学者对桥梁在静力[3-4]或者动力[5-6]作用下的整体变形与局部受力的状态进行了大量研究。Xu等[7]通过合理选取振型数量,并利用模态叠加法建立斜拉桥的动力方程,分析了车桥耦合作用下青马大桥的杆件应力与桥面板加速度。Zhang等[8]利用等效正交异性板法简化了正交异性桥面板的建模,并对车辆与风共同作用下桥梁的疲劳可靠性进行了分析。Li等[9]研究发现,由于钢桁梁桥自重较轻且货运列车质量较大,列车对桥梁振动响应影响显著。因此,需建立列车-桥梁耦合振动模型,以考虑列车和桥梁之间的动力相互作用对局部杆件内力的影响[5,9]。
为分析钢桁架梁桥节点板局部受力情况,往往需要对节点板采用较小的有限元网格划分尺寸。为避免对整桥采用统一精细化网格划分导致的动力分析计算工作量难以接受的情况[6],多尺度建模方法已被广泛应用于大型土木结构,如大跨度桥梁,大型场馆等的整体与局部受力分析中[10]。多尺度建模方法按照建模方式与计算过程可分为非耦合多尺度方法(Uncoupled Multi-Scale Method, UMS)[11]与耦合多尺度方法(Coupled Multi-Scale Method, CMS)[10]。其中,UMS将整体模型与局部精细化模型单独建模,首先计算出整体模型变形及内力结果,然后将其作为局部精细化模型的边界条件,并进行局部受力分析。UMS虽然具有计算效率高的优点,但是局部精细化模型的边界条件选取复杂,如果边界条件选取不当,就会导致局部分析结果产生较大误差[6,12]。CMS直接建立结构多尺度整体有限元模型,对需要考虑局部细节特性的部位采用精细模型和网格划分,而其余部位采用简化单元和较大网格划分,以同时反映局部细节特性与整体响应,及整体与局部间的相互影响[6]。CMS实现方式比较简单且计算结果更加准确[12-13]。因此,本文采用CMS对建立多尺度桥梁有限元模型,以同时考虑钢桁架梁桥的整体响应与节点板局部响应。
当采用自编软件开展列车-桥梁耦合系统局部动力响应分析时,通常需要编制复杂的后处理程序计算单元应力[9]。这种方案虽然灵活,但其前处理建模过程和后处理过程较为复杂,因此并不适用于考虑复杂构件局部响应的列车-桥梁耦合动力分析。而通用有限元软件(如Ansys)虽然有效解决了复杂模型建模和后处理问题,但在进行车桥耦合动力分析时,缺少专用轮轨非线性接触模型[14-15];同时,当采用接触单元模拟轮轨接触,轮轨间强非线性接触极大增加了动力分析计算量[16]。崔圣爱等[17]在Ansys中建立桥梁有限元模型并将其振型导入SIMPACK中进行车桥耦合动力分析。这种方法虽然可以通过SIMPACK软件模拟复杂的轮轨接触关系,但其利用模态叠加法建立桥梁结构动力方程,无法准确获得桥梁局部振动响应[9]。
综上所述,为充分利用有限元软件的精细化建模和后处理能力,降低车-桥耦合振动分析程序的开发难度,本文提出了基于Ansys-Matlab联合仿真技术开展考虑列车-轨道-桥梁耦合振动的钢桁梁桥局部应力分析的方法。在Matlab中利用多刚体动力学建立垂向车辆模型,在Ansys中建立桥梁有限元模型,通过Hertz弹簧模拟轮轨接触。分别在Matlab与Ansys中求解列车与桥梁的动力响应,并通过两个软件间的数据交换及轮轨间作用力与位移协调条件实现列车与桥梁的耦合。该方法既考虑了车桥耦合相互作用,又可以充分利用Ansys强大的后处理功能直接对桥梁各个单元应力进行计算与处理,简化了复杂单元的应力求解难度。
1 列车-轨道-桥梁耦合系统模型
1.1 车辆模型
由于引起桥梁动力响应的主要是竖向荷载,因此本文采用10自由度垂向车辆模型[18],每节车包含一个车体,两个转向架,四个轮对及连接转向架与轮对的一系悬挂与连接车体与转向架的二系悬挂。车体、构架与轮对都被模拟为刚体,忽略其弹性变形;一系悬挂与二系悬挂都被模拟为弹簧-阻尼单元。其中车辆自由度包括车体的沉浮zc和点头βc、转向架的沉浮zt1、zt2和点头βt1、βt2以及轮对的沉浮zw1、zw2、zw3、zw4,共10个自由度,车辆模型见图1。

图1 车辆模型
采用达朗贝尔原理,建立列车子系统动力方程为
(1)

1.2 轨道-桥梁模型
根据轨道-桥梁子系统不同构件的特性,在采用有限元方法建模时,钢轨、轨枕、桥梁主梁及承受弯矩的杆件都利用梁单元模拟,扣件利用弹簧阻尼单元模拟,局部节点板利用板单元模拟。建立桥梁模型后,Ansys可以自动形成结构的质量、阻尼、刚度矩阵。轨道-桥梁子系统动力方程为
(2)
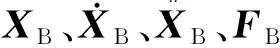
1.3 列车-轨道-桥梁耦合模型
列车子系统和轨道-桥梁子系统之间的动力相互作用通过轮轨接触关系实现。
列车-轨道-桥梁耦合系统的动力方程为
(3)
式中:FVB为桥梁给列车的作用力;FBV为列车给桥梁的作用力。
FVB与FBV可表示为
(4)
(5)
式中:n为总的轮对数;FVBi为第i个轮对所受轮轨力向量;FBVi为第i个轮轨对桥梁的作用力向量。
FVBi=[0,…,kh(zrwi-zwi),…,0]
(6)
FBVi=kh(zrwi-zwi)[0,…,N,…,0]
(7)
zrwi=XrwiN
(8)
其中,zwi为第i个轮对的竖向位移;zrwi为第i个轮对所在位置钢轨的位移,其可由钢轨单元的形函数N与单元节点位移Xrwi求得;kh为轮轨接触刚度,本文采用线性Hertz接触模型模拟轮轨关系,kh为[23]
(9)
其中,G为轮轨接触常数,m/N2/3;P0为静轮重,N。
2 Ansys-Matlab联合仿真方法
采用Ansys-Matlab联合仿真方法既可以考虑列车与桥梁间的相互耦合作用,又可以充分利用Ansys强大的后处理模块对桥梁单元应力进行提取与处理。根据式(3)所示的列车-轨道-桥梁耦合系统动力方程,在Matlab中建立列车动力方程,在Ansys中建立桥梁有限元模型,通过Matlab和Ansys之间的数据传输实现两个子系统之间的动力相互作用。Ansys和Matlab分别通过MatStep.txt文件与AnsStep.txt文件判断Matlab和Ansys计算是否完毕,Ansys-Matlab联合仿真计算流程见图2。
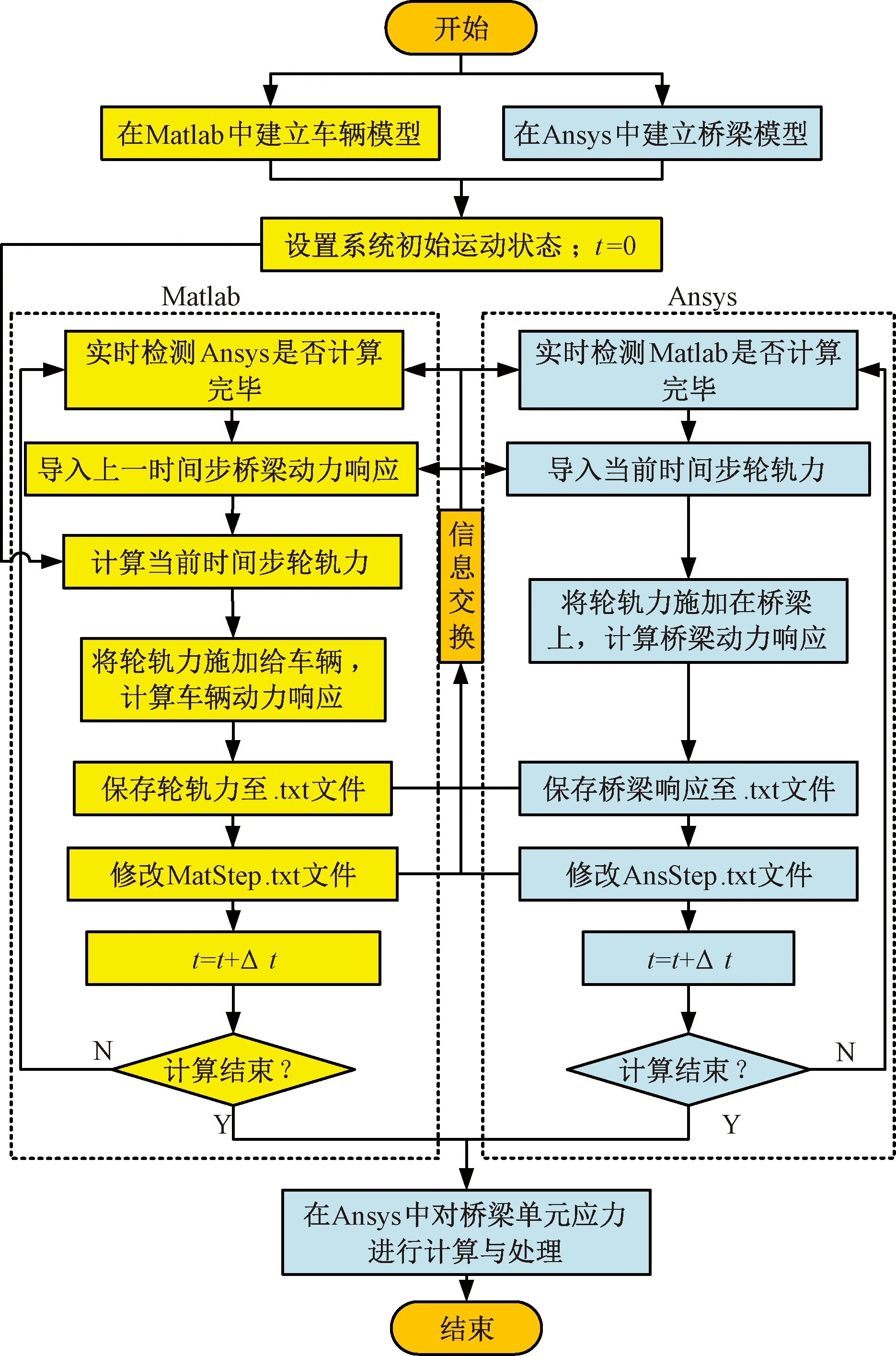
图2 Ansys-Matlab联合仿真计算流程
Step1进入当前时间步的计算时,Matlab实时检测AnsStep.txt中的值是否与当前时间步吻合,如果吻合,则导入上一时间步桥梁的响应,并更新轮轨力计算当前时间步列车的动力响应。
Step2Matlab将当前时间步的轮轨力写入一个文本文件,并将MatStep.txt中的值修改为当前时间步。
Step3进入当前时间步计算时,Ansys实时检测MatStep.txt中的值是否与当前时间步吻合,如果吻合,则导入当前时间步的轮轨力,并施加在桥梁上计算当前时间步桥梁的动力响应。
Step4Ansys将当前时间步桥梁的响应写入一个文本文件,并将AnsStep.txt中的值改为下一时间步。
对照组检查操作达到(24.36±0.56)h,研究组检查操作时间达到(0.51±0.09)h,组间比较。差异有统计学意义(P<0.05)。
Step5将下一时间步设为当前时间步,重复Step1~Step4直至计算完成。
需要指出的是,在Matlab中会根据列车速度与已运行时间识别与轮对接触的钢轨单元,同时将非节点轮轨力按照Hermite三次插值函数[24]分配至钢轨单元左右节点上,Ansys只需在相应节点上施加相应的力即可。此外,文献[25]指出当积分步长足够小时(一般取0.001 s的积分步长即可),车辆子系统与桥梁子系统间不迭代也可以获得准确的结果。因此,本文的Ansys-Matlab联合仿真方法未进行迭代,其结果经过验证是准确的。
3 桥梁概况和试验介绍
1991年通车的麻涌铁路桥横跨麻涌河,为南北走向(广州—东莞)单线简支钢桁架桥,正桥为明桥面,桥上为Ⅱ级专用线。桥全长752.31 m,其中正桥130.42 m,广州侧引桥327.49 m,东莞侧引桥294.40 m。正桥为2孔64 m简支下承式栓焊钢桁梁,每孔钢梁长65.10 m,桥墩中-中为65.24 m,麻涌桥桥型布置见图3。桥梁主桁中心距为5.75 m,桁高为11 m,所有杆件采用φ22(20 MnTiB)高强度螺栓连接。钢桁梁各杆件均采用16 Mnq钢材,钢材弹性模量取2.1×1011Pa,桥梁所有材料均假设为线弹性。桥面正线为50 kg/m钢轨,轨枕采用木枕。墩帽、墩身底节、墩承台均采用C25混凝土,墩身采用C20混凝土。桥面二期恒载包括人行道及避车台、检查设备以及轨道结构,总计613.1 kN。
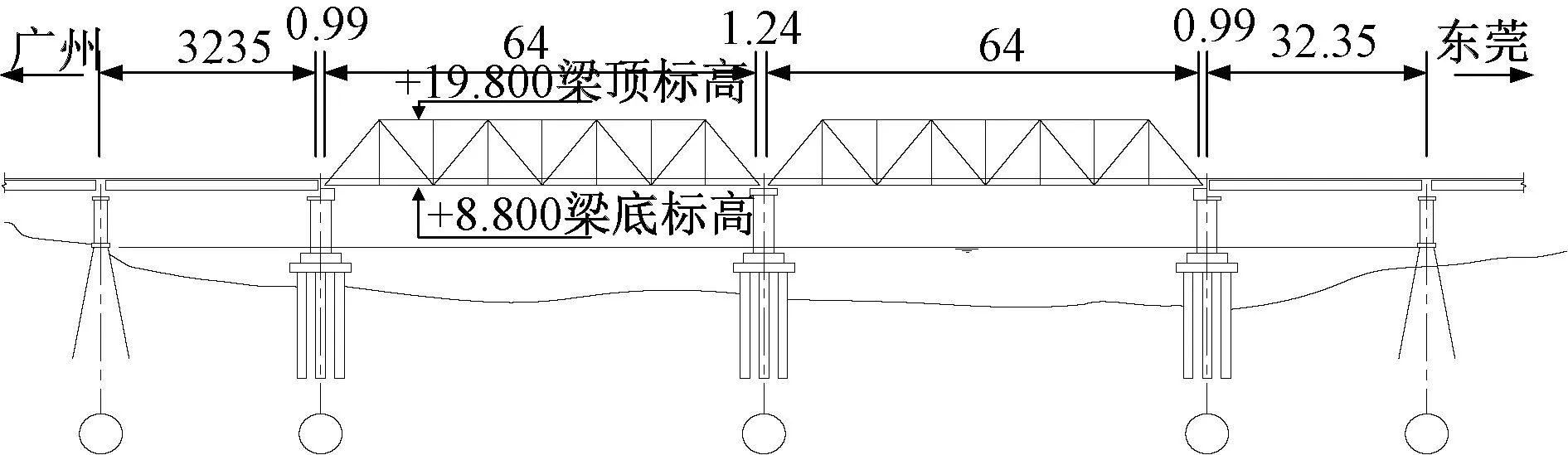
图3 麻涌桥桥型布置(单位:m)
为检验和评估钢桁梁桥的静、动力性能,并为理论分析方法提供试验数据验证,于2017年1月4日至2017年1月6日对该桥进行了静载试验、脉动试验和行车动力响应试验。杆件局部应变测试仪器采用DH3816 N动态信号采集分析系统,采样频率100 Hz,现场应变测试见图4。由于节点板的应力状态比较复杂,而杆件的应力状态比较明确(一般为轴向受力),所以为了测得两个测点各自的真实应力状态,在节点板上测点位置粘贴应变花测量,在下弦杆的测点位置粘贴沿杆件轴向的应变片测量。

图4 现场应变测试
4 多尺度有限元模型
4.1 模型介绍
为了研究钢桁架桥局部节点板上的应力响应,本文采用耦合多尺度方法(CMS)建立包含节点板的麻涌桥多尺度有限元模型。根据麻涌桥各个部分不同的构件特征,采用Beam单元模拟钢轨、桁架杆系结构、主纵梁、主横梁以及桥墩;在节点板区域采用Shell单元精细化建模模拟,而节点板以外的杆件结构仍然采用Beam单元模拟;为了简化分析,本次多尺度建模仅对E4节点板区域进行了精细化模拟,麻涌铁路桥多尺度有限元模型及应变测点布置示意见图5。各类主要构件所对应的单元类型见表1。由于麻涌桥为明桥面,钢轨扣件及轨枕与纵梁连接件采用弹簧阻尼单元模拟。钢轨扣件刚度取6×107N·m,阻尼取7.5×104N·s/m;轨枕与纵梁连接件刚度取5.1×107N·m,阻尼取2.0×105N·s/m。

图5 麻涌桥多尺度有限元模型及应变测点布置示意

表1 模型各构件单元类型说明
E4节点精细化模型通过在Shell单元端部创建MPC184刚性梁单元来模拟Shell单元和Beam单元的连接。同时,为了消除两种类型单元在连接区域的应力集中效应,Shell单元的边界应该远离节点足够的距离。根据文献[26],将各杆件长度取为由节点处的端面向外延伸3倍腹板高度的长度(即3×460 mm=1 380 mm)。这种多尺度的混合模型既满足了节点板分析的精度要求,又保证了节点板以外结构的分析效率。
本次麻涌铁路桥只对广州侧单跨64 m钢桁架及其对应桥墩采用有限元软件Ansys进行了多尺度建模。另外,为模拟列车进、出桥的运动状态和桥梁两端的边界条件,在桥梁两端各延长了31 m的轨道延长段。
4.2 试验验证
为了验证麻涌桥多尺度有限元模型的正确性,对比了麻涌桥在静载作用下跨中和四分之一跨处的竖向位移,静载工况加载见图6,计算值和现场实测值的对比结果见表2。
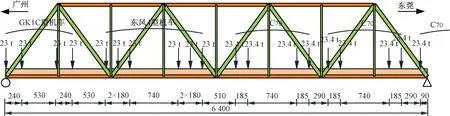
图6 静载工况加载示意(单位:cm)

表2 静载工况竖向位移对比结果
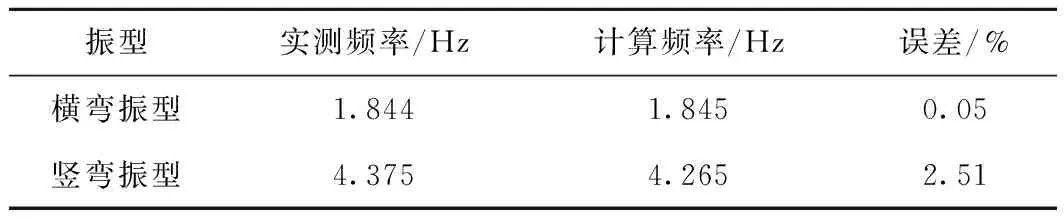
表3 麻涌桥自振频率

图7 麻涌桥主要振型
为进一步检验基于Ansys-Matlab联合仿真的列车-轨道-桥梁耦合振动分析方法的准确性,以图5所示的E4节点板上测点和下弦杆内侧翼缘测点的动应变为例,分别对比联合仿真方法的数值计算结果和现场实测结果。
试验实际行车编组为“1节机车+20节C70满载+1节C70空载+21节C70满载+1节C70空载+8节C70满载”,列车以26 km/h的速度通过桥梁。Ansys-Matlab联合仿真方法时间积分步长为0.000 2 s,轨道不平顺类型采用美国5级谱。节点板测点和下弦杆测点的应变时程曲线实测值和计算值对比见图8。
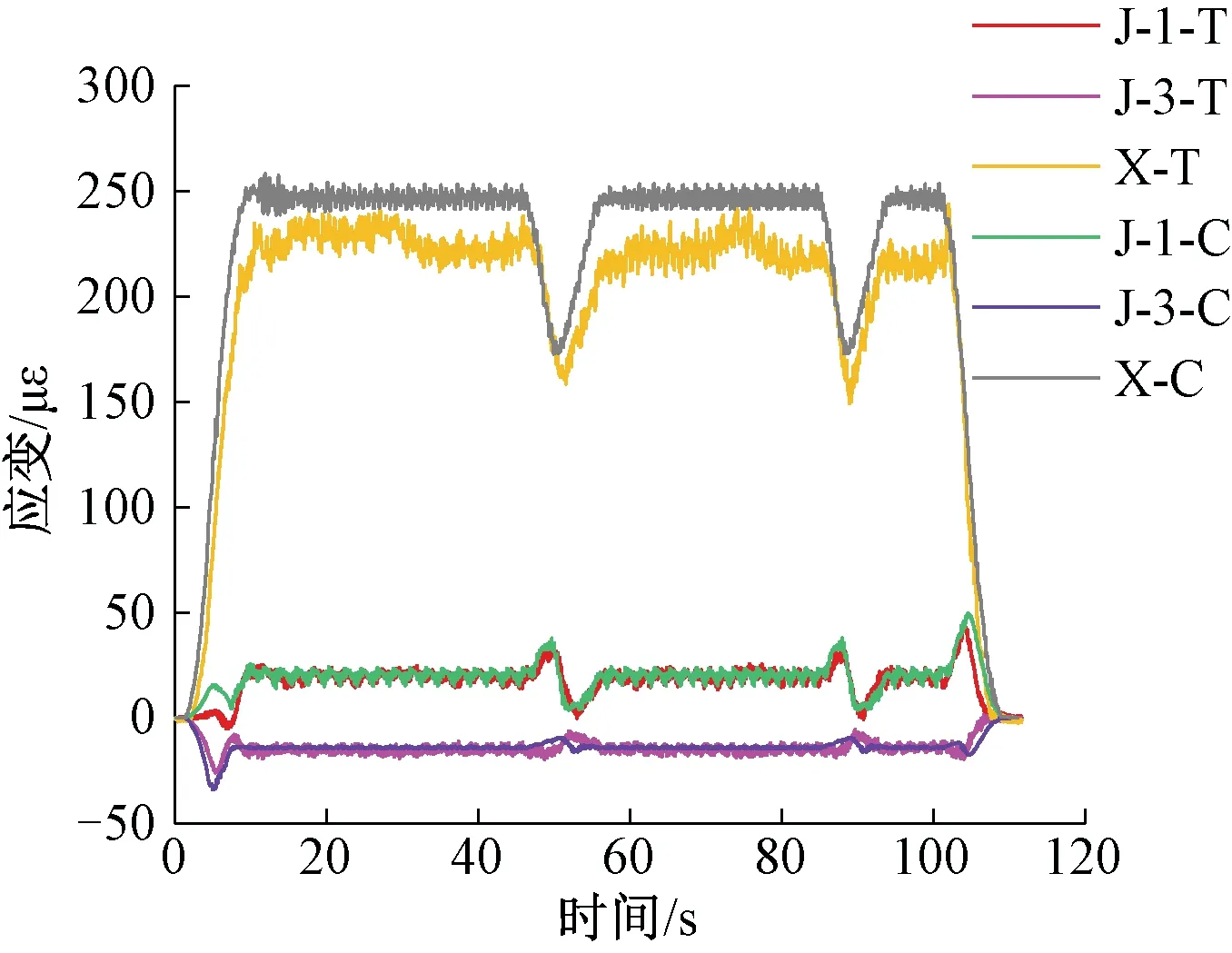
图8 E4节点板上测点应变时程计算值和实测值对比
由图8可知,对于节点板和下弦杆测点的应变均值,试验实测值和计算值均吻合较好,其中下弦杆应变实测值均值、计算值均值分别是230×10-6、245×10-6,二者误差6.52%。综上所述,本文基于Ansys-Matlab联合仿真的列车-轨道-桥梁耦合振动分析方法可以准确借助多尺度模型准确反映桥梁的局部应力响应。
5 钢桁梁桥局部应力响应分析
5.1 计算工况
为研究列车引起的钢桁梁桥局部应力响应特征,本节基于上述的Ansys-Matlab联合仿真方法开展动力响应计算,并采用Ansys后处理模块进行应力分析,本节提到的应力均为米赛斯应力。
根据麻涌桥实际行车情况,选取两种编组列车形式为“1节机车+9节C70重载货车”(C70编组)和“1节机车+9节C80重载货车”(C80编组),分别以40~120 km/h(按20 km/h递增)之间5种速度行驶过桥,行车方向为广州方向开往东莞方向。通过对多尺度模型开展静载工况分析见图6,得到E4节点板内侧应力分布状态见图9。然后在其中选取4个较易出现应力集中现象的点作为关注点,4个关注点(1#~4#)在节点板上的位置见图9。
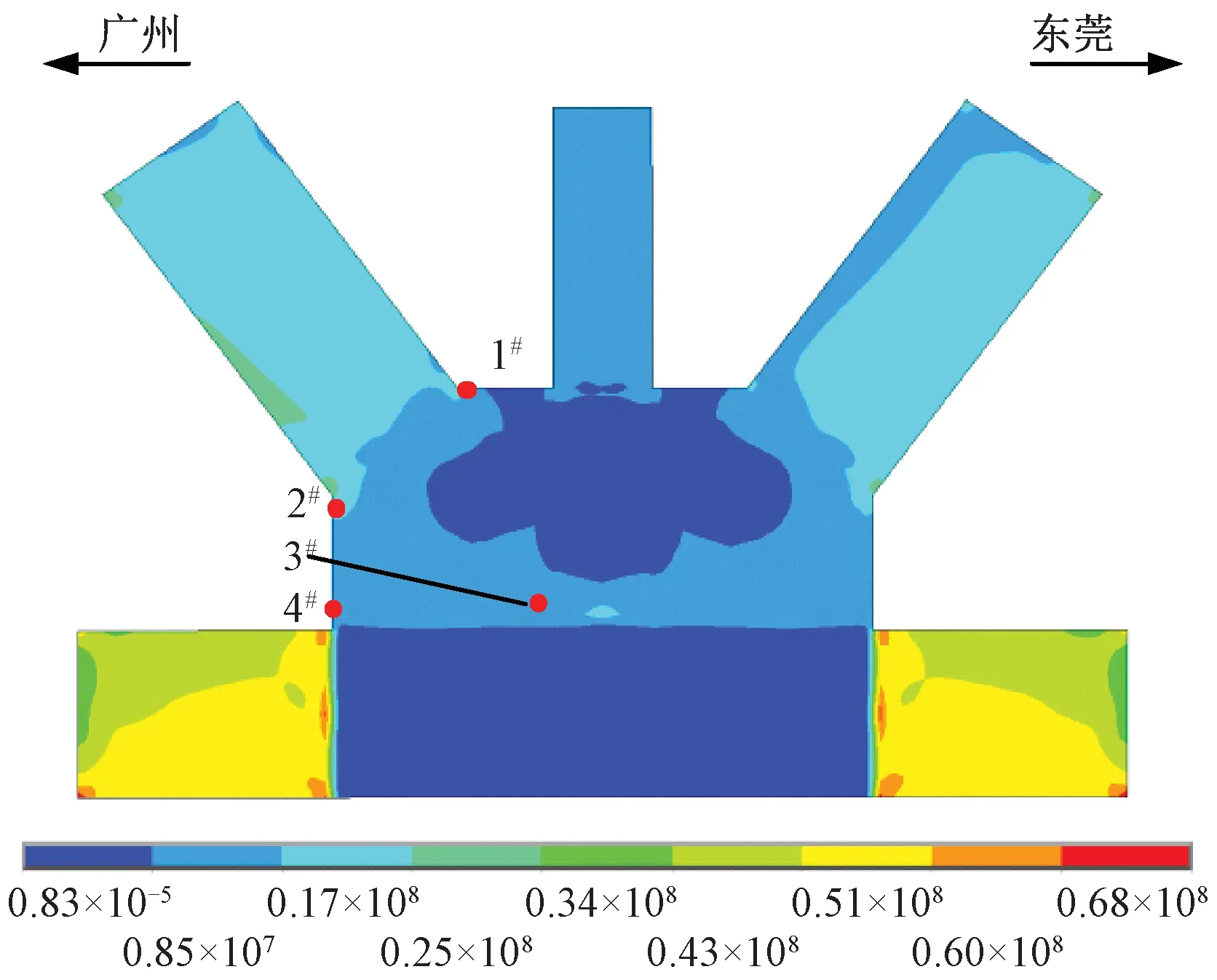
图9 E4节点板内侧应力分布状态(单位:Pa)
5.2 轨道不平顺的影响
本节考察了C80编组列车在通过麻涌桥时,轨道不平顺对桥梁响应的影响。考虑美国5级轨道不平顺谱和不考虑轨道不平顺时,2#点的应力响应见图10。由图10可知,由于简支钢桁梁桥质量小,且采用明桥面,考虑轨道不平顺后货车引起的桥梁应力响应变化幅度显著增大。因此,后续工况均考虑了轨道不平顺的影响。

图10 轨道不平顺对桥梁应力响应的影响
5.3 局部应力响应分析
两种编组列车分别在5种车速下通过桥梁时的最大应力值见图11,两种编组列车以100 km/h的设计速度行驶过桥时各关注点的应力时程图见图12,两种编组列车在不同车速下2#点的应力时程图见图13,采用雨流计数法对2#点应力时程曲线上不同大小的疲劳应力幅出现次数统计见图14。

图11 各关注点最大应力值随车速的变化规律
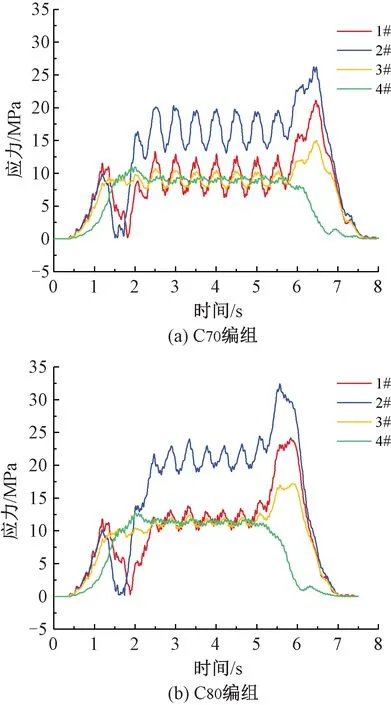
图12 车速为100 km/h下各关注点的应力时程图
由图11可知,节点板上各点的最大应力值随着车速的变化而略有波动,不同编组类型的列车引起的这一变化趋势并不相同,其中C70编组列车引起的最大应力值随车速的增加呈缓慢上升趋势;而C80编组列车车速在60 km/h时,引起的各点最大应力值最大。由图12可知,列车经过桥梁时,节点板上各点动应力响应不同,其中2#点应力值最大;1#点和2#点应力时程曲线波动幅度较大,车桥耦合振动效应明显。由图13可知,C80编组列车以60 km/h通过桥梁时车体与桥梁发生了较为明显的共振现象。
综合图13和图14可知,两种编组列车以不同速度通过桥梁时,2#点的疲劳应力幅主要集中在0~2.5 MPa之间;当C70编组列车车速分别为100、120 km/h时,高应力幅(2.5~7.5 MPa)的疲劳应力循环次数较多,C80编组列车为60 km/h时由于共振,高应力幅的疲劳应力循环次数较多;C80编组列车由于轴重更大,因此所引起的2#点最大疲劳应力幅要大于C70编组列车。
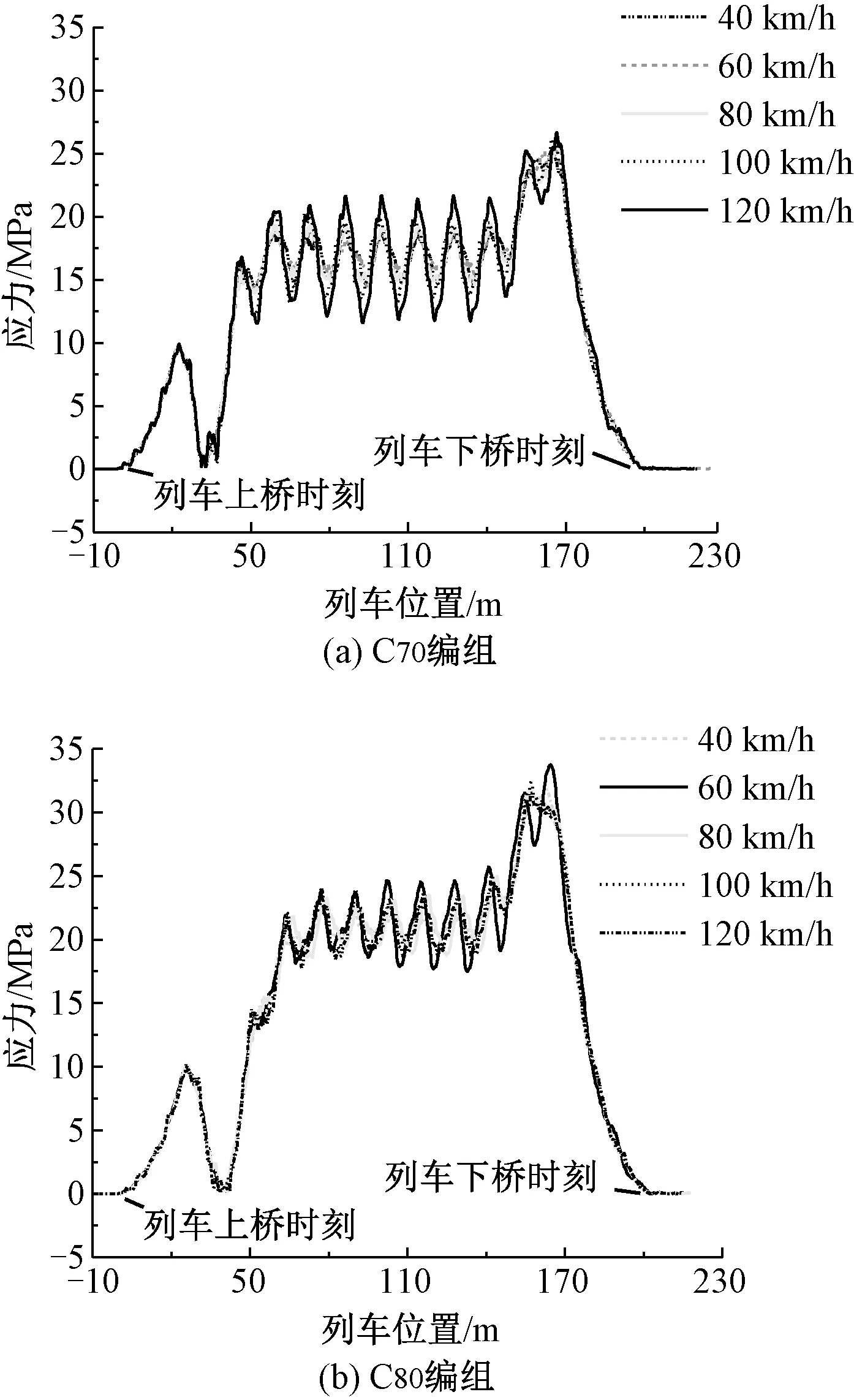
图13 两种编组列车在不同车速下2#点的应力时程
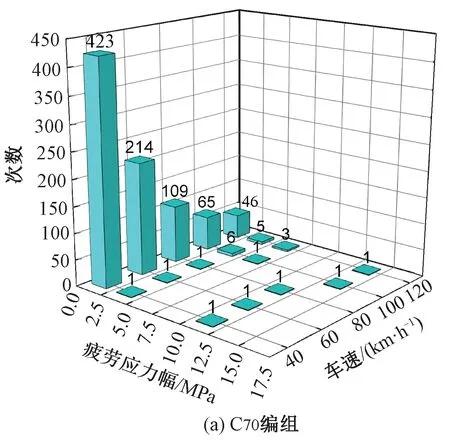

图14 2#点雨流计数结果
综上所述,车速对节点板的最大应力值响应影响不大,但不同车速引起的高应力幅的疲劳应力循环次数不同。
6 结论
本文基于车-桥耦合振动理论,在Matlab中建立车辆动力学模型,在Ansys中建立桥梁多尺度有限元模型,提出了基于Ansys-Matlab联合仿真的列车-桥梁耦合动力响应分析方法。并以广州麻涌铁路桥为研究对象,采用该方法分析了列车以不同编组和不同车速通过钢桁梁桥时节点板的局部应力响应,得到了以下结论:
(1) Ansys-Matlab联合仿真算法既考虑了列车与桥梁间的耦合作用,又避免了在后处理中自编程序计算单元应力,简化了车桥耦合动力分析中桥梁复杂单元动应力计算的难度。
(2) 在不同编组列车和不同车速工况下,钢桁梁桥节点板与桁架斜杆连接处的2#点应力最大值和应力波动幅值均为最大。
(3) 车速对节点板的最大应力值响应影响不大,但不同车速引起的高应力幅的疲劳应力循环次数不同。

