橡胶减振垫频变的CRTSⅢ型板式无砟轨道自振特性分析
孙 旭,赵才友,王 平
(1.高速铁路线路工程教育部重点实验室,四川 成都 610031;2.西南交通大学 土木工程学院,四川 成都 610031)
黏弹性材料质量轻、经济、可靠性高,能够有效抑制结构振动和降低噪声水平,在薄板、壳体等构件中已经得到了广泛应用[1]。在轨道结构的减隔振设计中也多采用增加黏弹性元件,如减振型扣件、阻尼钢轨、轨枕垫层、道砟垫层等[2]。普通CRTSⅢ型板式无砟轨道主要由钢轨、扣件、轨道板、自密实混凝土和底座板构成。而减振型CRTSⅢ型板式无砟轨道则在底座板和自密实混凝土之间增加了橡胶减振垫,以降低轨道结构共振频率,从而起到降低环境振动的效果。已有研究表明[3-5],橡胶减振垫有显著隔振作用,铺设橡胶减振垫后可以明显减小底座板及其下部结构的振动,但也会增加橡胶减振垫上部的轨道板、钢轨的振动。
轨道结构计算模型中对橡胶黏弹性材料的动态特性大多进行常量化处理,而橡胶黏弹性材料的动参数具有明显的频率依赖性[6-7],为了更准确地预测轨道结构的动力学响应和优化结构性能,国内外已经开展了对扣件胶垫动态特性及其对轨道结构系统影响的研究。Wei等[8]采用车辆-轨道垂向耦合系统动力计算模型分析了频变、幅变扣件胶垫特性下的时域响应,研究表明扣件胶垫的频变特性能明显增大轮轨间相互作用,增大轮重减载率。采用频变刚度的扣件胶垫分析钢轨的垂向自由振动,能够提高钢轨垂向敏感共振频率及其振型的预测精度[9]。Oregui等[10]通过力锤试验研究了有砟轨道结构的动力特性,指出计算模型采用频变刚度的扣件胶垫可以更好的符合试验模态频率和振型。
目前对于减振型CRTSⅢ无砟轨道的研究多集中于橡胶减振垫采用常量参数来评估其在轨道系统中的减隔振效果,考虑橡胶减振垫频变特性对轨道结构动力特性的研究鲜见报道。本文首先通过DMA试验获得橡胶减振垫试件在200 Hz范围内随频率改变的复模量,然后基于实测的复模量计算得到橡胶减振垫动刚度,最后建立减振型CRTSⅢ板式无砟轨道有限元模型,同时将Winkler弹性地基上四边自由板的近似解与有限元结果对比,研究橡胶减振垫频变特性对轨道结构固有频率和振型影响。
1 橡胶减振垫复刚度试验研究
采用DMA Q800型动态热机械分析仪对橡胶减振垫试件进行变频率动态测试,试验设定恒温25.8 ℃,频率为0.01~200 Hz,步长为4 Hz。试件尺寸为23.9 mm×8.1 mm×2.4 mm,密度为0.98 g/cm3,泊松比为0.44。试件两端固定夹持进行恒定力下拉伸测试,得到实测的动态模量和损耗因子随频率变化曲线,如图1所示。复模量E*和损耗因子δ计算公式为
(1)
tanδ=E″/E′
(2)
式中:σ*、ε*分别为复数形式的应力和应变;δ为损耗角;储存模量E′=|E*|cosδ;损耗模量E″=|E*|·sinδ。
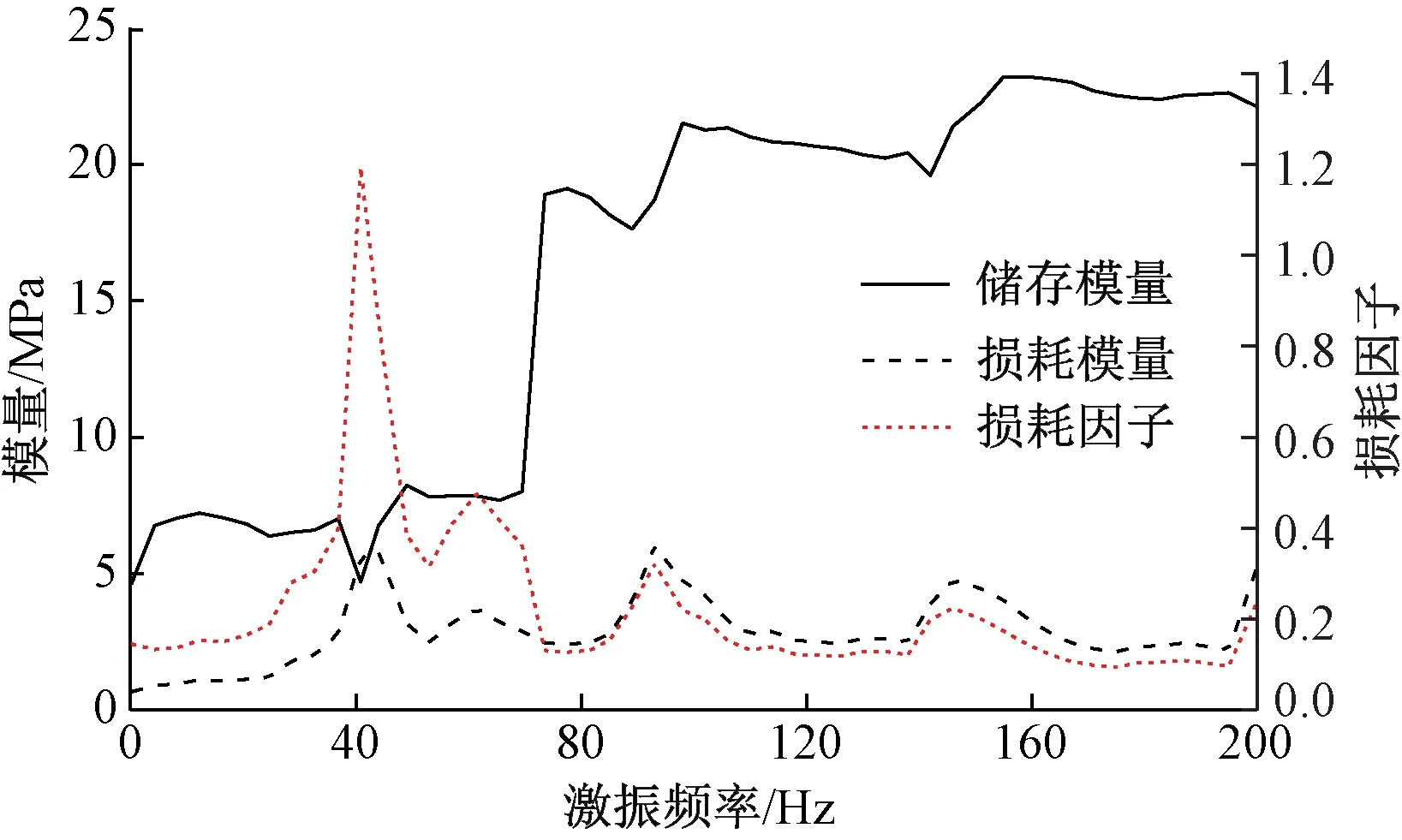
图1 实测橡胶减振垫试件复模量
储存模量、损耗模量和损耗因子分别反映材料的弹性、黏性和能量损失。由图1可知,当激振频率小于41 Hz时,E′、E″ 和δ都较小,且随频率变化不大,这时材料表现为高弹性;在41 Hz附近损耗因子δ达到峰值1.12,此时材料的黏性已经超过弹性,能量损失较大,E′也达到峰值;此后,储存模量E′在70 Hz附近随频率的增大而急剧增大,表现为刚性,E′很高,E″ 和δ都很小,且随频率变化不大。
相关研究表明[11],轨道不平顺激发的振动,其频率多在包含轮轨系统同相共振频率和钢轨与轨枕反相共振频率的0~200 Hz低频段,故本试验分析的频率范围为0.01~200 Hz。此外,由列车移动荷载引起的地面振动频率范围为2~200 Hz[12]。可见,对于分析轨道刚度、轨道结构低频振动以及列车引起的地面振动,选择0.01~200 Hz频段较为合理。
2 橡胶减振垫动刚度计算
黏弹性材料的频变复模量会产生频变刚度[13],频域内黏弹性材料的运动方程可以表示为
[-Mω2+K(ω)(1+jδ(ω))]X(ω)=F(ω)
(3)
式中:ω为角频率;M为质量矩阵;K(ω)为刚度矩阵;δ(ω)为损耗因子矩阵;X(ω)、F(ω)分别为节点位移列阵和外力列阵的傅里叶变换。
系统动刚度D(ω)为
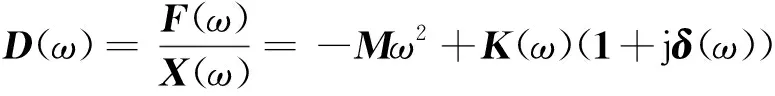
(4)
系统动刚度与质量、频变刚度、频变损耗因子有关,而质量和刚度与结构的几何尺寸、形状密切相关,因此动刚度的影响因素较多,为更准确描述黏弹性材料的频变特性,采用实测的频变复模量和损耗因子计算橡胶减振垫的动刚度。橡胶减振垫(图2)为具有特殊的钉柱结构的橡胶层,钉柱呈周期性分布且具有对称性,柱钉尖端半径R0=8 mm,柱钉底端半径R1=28 mm,柱钉高H0=19 mm,覆盖层长方体边长B=66 mm,高度H1=10 mm。

图2 橡胶减振垫示意
将周期性分布的橡胶减振垫简化为单个钉柱,柱钉覆盖层长方体周边施加对称约束。为分析简化计算模型边缘效应的影响,分别建立包含k×k(k=1、3、5、9、11)个柱钉的橡胶减振垫实体有限元模型,以每个模型中心位置处的一个柱钉为研究对象,所有模型的柱钉尖端面施加固定约束,对单个柱钉模型的覆盖层长方体周边施加对称约束,其他模型周边自由无约束,由此对比分析单个柱钉周边采用对称约束边界条件的影响。采用Comsol Multiphysics进行频域分析,覆盖层长方体底面施加垂向的单位面压力谐波荷载,扫频范围为0~200 Hz,X(ω)为研究对象受力面上所有节点垂向位移幅值的平均值。其中包含单个柱钉和3×3个柱钉的橡胶减振垫有限元模型,如图3所示,计算得到所有模型的动刚度如图4所示。
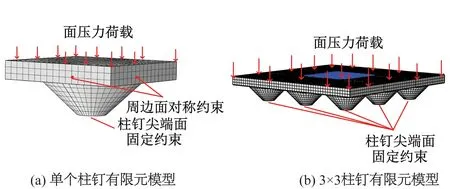
图3 橡胶减振垫有限元模型

图4 橡胶减振垫动刚度
将各有限元模型分别简称为Ck模型,k值越大,则计算模型越接近真实的轨道结构橡胶减振垫尺寸和受力状态。由图4可知,在0~74 Hz范围内各模型的动刚度值相差不大,在74 Hz之后各模型动刚度基本上随着k值的增大先逐渐减小至C5模型,而后逐渐接近C1模型。若以C1模型动刚度值为基准,C5模型和C11模型与C1模型在各频率下动刚度的最大差值分别为7.2%、1.8%,而同等条件下C5模型和C11模型的计算时间分别增至C1模型的10倍和80倍。因此,综合考虑计算效率和精度,采用C1模型计算整个橡胶减振垫的动刚度是合理的。由图4和图1对比可知,橡胶减振垫动刚度与储存模量的变化趋势比较接近,损耗因子对动刚度影响较小,橡胶减振垫静刚度为22.0 MPa/m。
3 CRTSⅢ板式无砟轨道自振特性分析
DMA试验表明,橡胶减振垫的复模量具有明显的频变特性。由此计算得出橡胶减振垫的动刚度也随外部激励频率而改变。因此,采用频变特性橡胶减振垫时,不同激振频率下橡胶减振垫刚度会有所不同,由此整个轨道结构系统的动力特性也会随之改变。为探究橡胶减振垫频变特性对轨道结构系统的固有频率和振型的影响,计算橡胶减振垫采用常量参数(0 Hz处取值)和频变参数两种工况,其中常量参数的损耗因子采用图1中实测损耗因子的初始值0.15;频变参数的动刚度采用C1模型计算的参数,损耗因子采用图1中的实测值。
3.1 CRTSⅢ型板式无砟轨道有限元模型
CRTSⅢ型板式无砟轨道采用预制轨道板结构,以“路基纵连、桥上单元”的基本原则为总体设计思路[14]。路基上板间用预应力钢棒或普通锁扣连接,支承在素混凝土支承层上;桥梁上和隧道内轨道板为单元板,板间无连接,支承在钢筋混凝土底座。考虑单元轨道板的下部结构(桥面板和隧道仰拱)刚度较大,将其简化为刚性面。因此,根据减振型CRTSⅢ型板式无砟轨道特点进行合理简化,建立有限元模型,如图5所示。其中,轨道板和自密实混凝土形成紧密连接的“复合板”结构,均采用实体单元模拟,不考虑钢轨和扣件系统,并忽略自密实混凝土的限位凸台。橡胶减振垫采用面弹簧-材料阻尼单元。考虑一块单元板长度,单元板四边自由无约束。模型主要计算参数见表1。

图5 CRTSⅢ型板式无砟轨道有限元模型
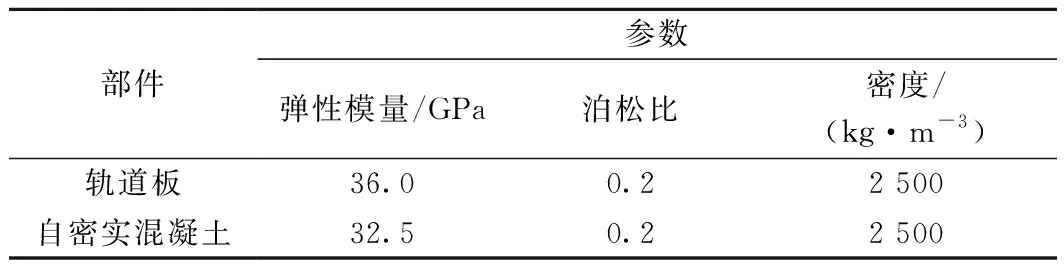
表1 有限元模型主要计算参数
3.2 计算模态分析
3.2.1 固有频率和振型
Comsol Multiphysics采用隐式重启动Arnoldi算法求解广义复特征值问题。有限元模型只采用了垂向的计算参数,因此只提取轨道结构可出现垂向分量的振动,忽略横向、纵向平动和水平面转动的整体振动。计算200 Hz内的固有频率和振型,其中橡胶减振垫采用常量工况时轨道结构前6阶固有频率和振型,如图6所示。
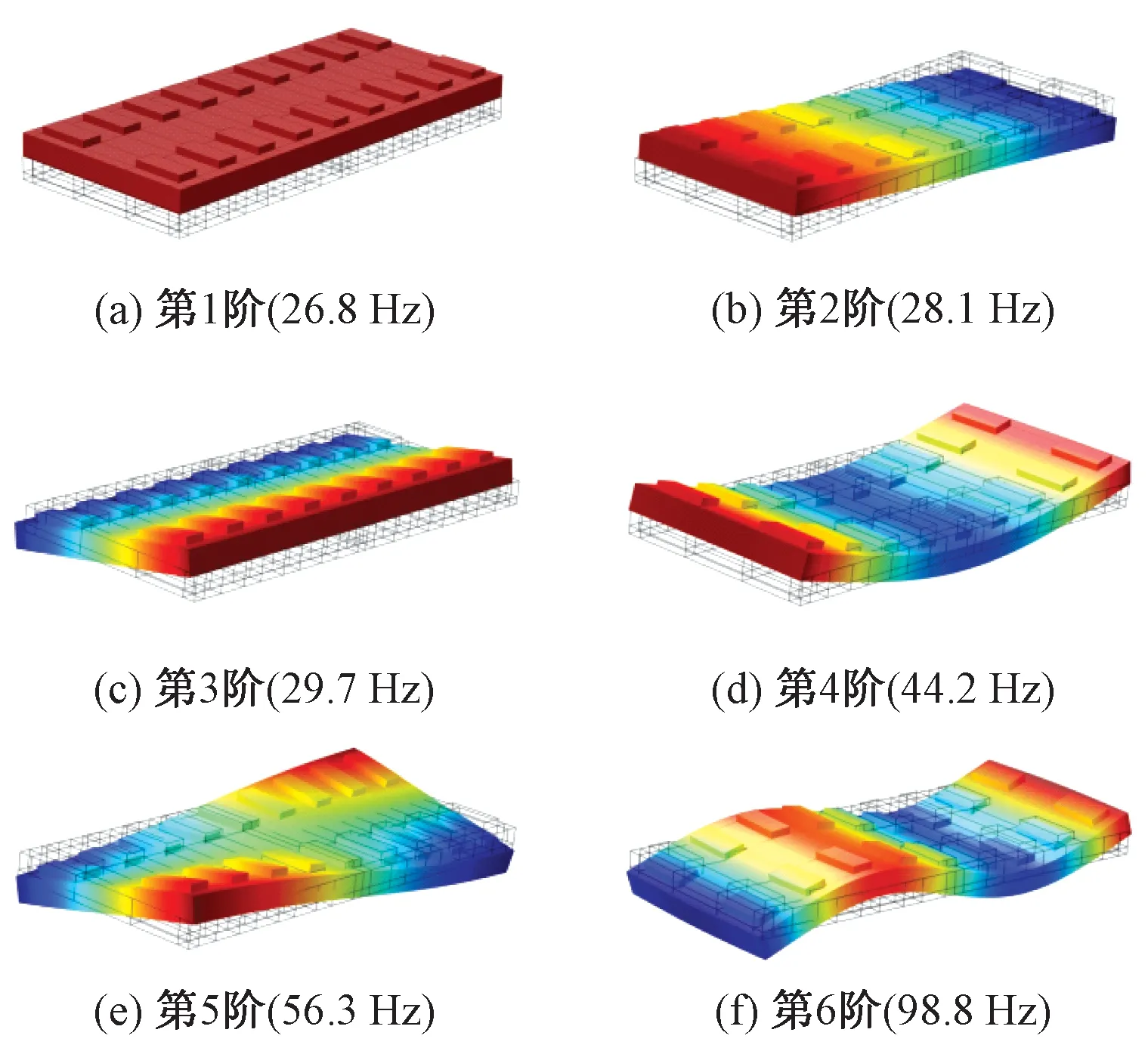
图6 前6阶模态频率和振型
前3阶为整体振动,分别为垂向平动、纵向转动和横向转动。对于弹性模态,设m、n分别代表阵型纵向、横向的1/4正弦函数波,则第4、5、6阶振型分别用(m=2、n=0),(m=1、n=1),(m=4、n=0)表示。当橡胶减振垫采用频变参数时,轨道结构的固有频率也将随着橡胶减振垫受到的激振频率的变化而改变。频变条件下轨道结构前6阶固有频率随激振频率的关系曲线如图7所示。

图7 轨道结构固有频率随激励频率的影响曲线
为便于观察对比,将橡胶减振垫动刚度随激振频率的变化一起绘于图7。从整体趋势看,轨道结构各阶固有频率与橡胶减振垫动刚度变化趋势相近,但橡胶减振垫频变对整体振动和弹性模态固有频率的影响不同。前三阶整体振动固有频率与橡胶减振垫动刚度呈正相关,变化趋势相近。而弹性模态,即板的弯曲模态受橡胶减振垫动刚度的影响较小,并且随着轨道结构模态阶数的提高其影响越小。各阶模态振型则不受橡胶减振垫频变的影响,仍与图6中的规律一致,这在3.3节中的弹性地基上四边自由板的近似解中表现更明显。
3.2.2 橡胶减振垫频变时的敏感共振频率和振型
文献[9]研究钢轨-扣件系统时提出的扣件胶垫频变刚度下敏感共振频率概念,轨道板-橡胶减振垫系统可以参考。当橡胶减振垫动参数频变时,亦即橡胶减振垫动参数随着外激励荷载频率的变化而改变时,轨道结构固有频率也将与外部激振频率相关。若外部激振频率为fi时,橡胶减振垫动刚度为ki,损耗因子为δi,在此参数下可计算出轨道板-橡胶减振垫系统的一组n阶固有频率。当其中的某阶固有频率与外部激振频率一致时,该阶固有频率为敏感共振频率,其对应的振型为敏感共振振型。据此采用Comsol Multiphysics参数化扫描方式,求解与激励频率fi临近的几阶固有频率,找到与激励频率一致的固有频率和对应的振型,计算流程如图8所示。

图8 频变参数下轨道结构敏感共振频率计算流程图
由图8计算流程可以得到橡胶减振垫频变工况下轨道板在200 Hz内的敏感共振频率,如图9所示。通常阻尼对结构固有频率影响较小,而橡胶减振垫频变刚度值均大于静刚度值(图4),因此相同模态阶次轨道结构的固有频率在频变工况时大于常量工况。频变工况下并非每阶都有轨道结构敏感共振频率,在本文计算参数和容差范围内,轨道结构第3阶横向整体转动和第11阶(m=1,n=2)弯曲模态没有敏感共振频率和振型。

图9 轨道结构敏感共振频率
3.3 弹性地基上四边自由板的振动
将橡胶减振垫视为Winkler弹性地基,上述有限元模型可以转化为弹性地基上四边自由板的振动问题。轨道板和自密实混凝土组成的“复合板”厚度h=0.29 m,板宽b=2.5 m,h/b<1/8,可以采用薄板理论[15]。目前,针对四边自由矩形板的振型函数和固有频率精确解研究相对较少,难以找到既满足平板弯曲控制方程又满足自由边界条件的振型函数表达式。目前的处理方法大多为寻找振型函数的近似解[16]。本文采用双向梁函数组合法[17]求解弹性地基上四边自由矩形板的自由振动问题。梁函数组合法实质上为里兹法的一种具体应用,虽然为近似解,但方法简单,适用一般性边界条件,且在较少的项数下即能达到足够精度。Winkler弹性地基上板横向自由振动的微分方程为
(5)
(6)
式中:w为位移;D为板的弯曲刚度;ks为基床系数;ρ为板的质量密度;E为板的弹性模量;ν为泊松比。
相应的阵型方程为

(7)
(8)
固有频率为
(9)
弹性地基板的振型方程和边界条件不变,因此弹性地基上板的振型完全同无地基板。梁函数组合法的具体计算过程可参考文献[17],据此方法采用Matlab软件编制弹性地基上四边自由矩形板的自由振动程序,采用与上述有限元模型相同的计算参数,与有限元计算结果进行对比。图10为由梁函数组合法计算得到的第2阶纵向整体转动和第4阶弹性模态固有频率近似解与橡胶减振垫动刚度变化关系的曲线。图11为对应的归一化振型。
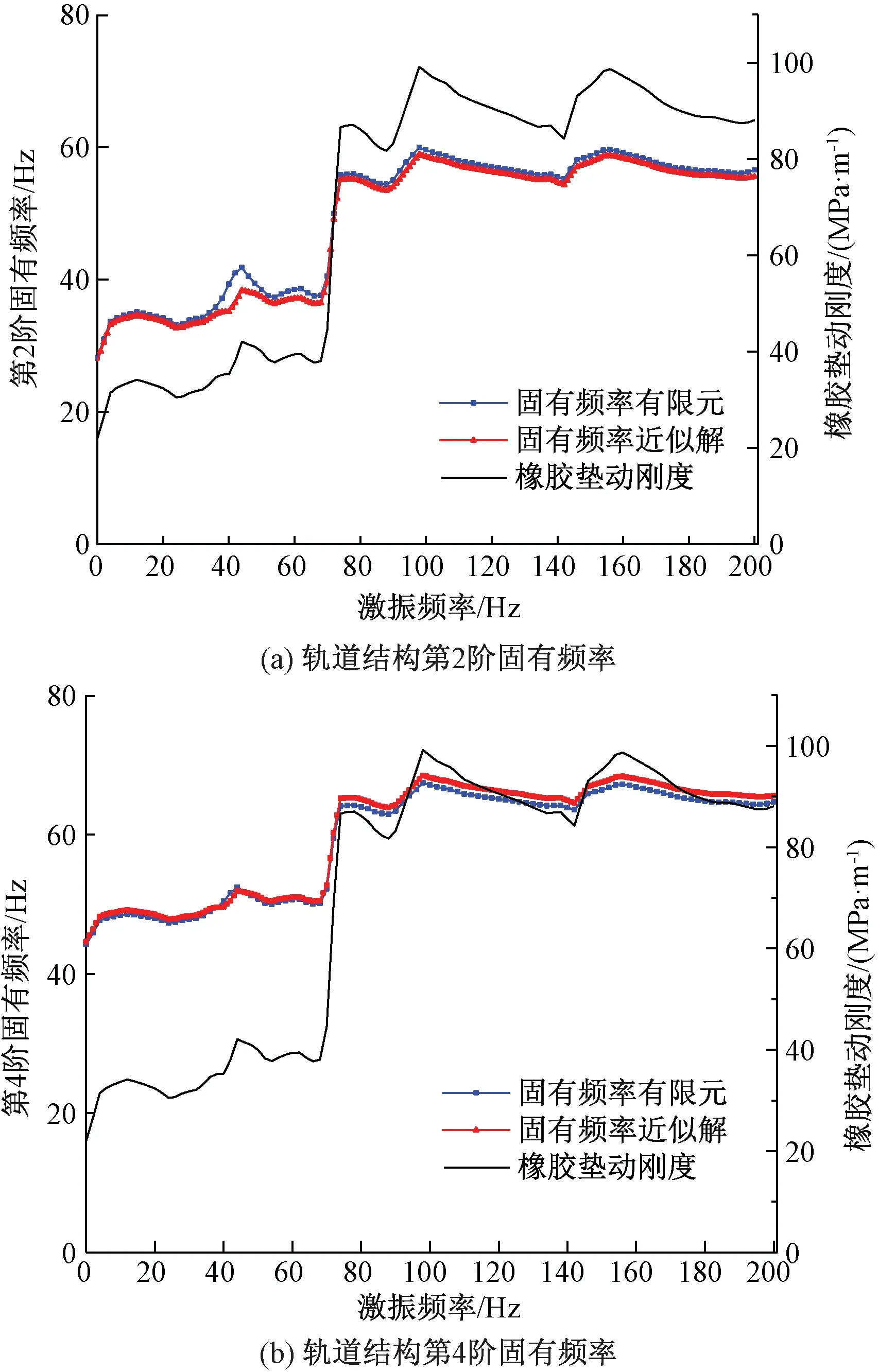
图10 轨道结构固有频率近似解


图11 梁函数组合法的轨道结构归一化阵型
4 结论
本文基于DMA实测复模量计算了橡胶减振垫的动刚度,建立了减振型CRTSⅢ板式无砟轨道模型,研究了橡胶减振垫频变特性对轨道结构固有频率和振型的影响,并采用近似解验证了有限元模型的正确性,得到如下主要结论:
(1)橡胶减振垫试件DMA试验表明,在41 Hz附近损耗因子达到峰值,能量损失较大,随后储存模量发生显著提高,这直接导致橡胶减振垫动刚度随储存模量产生较大变化。
(2)有限元模型和梁函数组合法近似解对比结果都表明,橡胶减振垫动刚度对板的整体振动和弹性模态固有频率的影响是不同的。整体振动固有频率与橡胶减振垫动刚度平方根成正比。橡胶减振垫动刚度越小,模态阶数越高,则板的弯曲模态受橡胶减振垫动刚度的影响越小。各阶模态振型则不受橡胶减振垫频变的影响。
(3)将敏感共振频率和振型概念应用于轨道板-橡胶减振垫系统,频变下轨道结构并非每阶都有敏感共振频率和振型,常量工况下轨道结构第3阶横向整体转动和第11阶(m=1,n=2)弯曲模态在频变工况则没有出现敏感共振频率和振型。
(4)轨道结构含有黏弹性部件时,建议考虑其频率依赖特性以提高结构动态特性预测精度。

