周期激励下的风机塔架模态识别方法
胡嘉苗,杭晓晨,朱 锐,曹芝腑,姜 东,
(1.南京林业大学机械电子工程学院,南京210037;2.东南大学空天机械动力学研究所, 南京211189)
准确获取风机塔架的模态参数对于及早发现风机异常、避免风机事故具有至关重要的作用[1]。通过结构模态辨识可得到结构的固有频率和振型,其被广泛应用于振动系统分析、振动故障诊断与预测、结构动力优化设计、结构损伤检测等方面[2–3]。由于实际环境中模拟风力机的载荷困难,且由于塔筒细长、钢壁较薄等,难以制作缩比试验模型,以及载荷特殊输入量难测量等问题,运行模态分析(Operational modal analysis,OMA)作为一种基于实测数据的分析工具,在研究风力机动力学特性方面具有广阔的应用前景[4–5]。结构动力学领域最早应用于风机模态参数测试的OMA算法是James和Carne的自然激励技术(Natural excitation technique,NExT)[6–7],该技术不依赖于人工激励,大大加快了数据采集速度。目前,环境激励下模态参数识别方法主要有:峰值拾取法[8]、时间序列法[9]、随机减量法[10]、NExT 法、随机子空间法[11]等。
由于周期性的重力、气动载荷作用以及转子旋转等因素,运行中的风机的稳定性分析应该在一个周期性的框架内进行[12–13]。在过去的十几年间,子空间模态辨识算法得到了飞速发展,并且在多输入-多数出(Multiple-input multiple-output,MIMO)系统辨识领域取得极大的成功[14–15]。然而现有的时域方法都是考虑在平稳的白噪声激励下的情况,对于激励中含有周期成分的情况研究较少[16]。为了识别运行中的风机塔架的模态参数,选择一种能够识别具有大量测量通道的周期系统的算法是很重要的。Allen 等[17–18]确定了在运行中的风机的周期性振型,但精度较低。Yang等[19]识别出了风力涡轮机叶片的高分辨率模态振型,但这些振型是在转子不工作时的静态振型。Verhargen 等最早提出了MOESP 算法[20],该算法直接从输入输出数据中估计出系统广义能观空间的基底从而完成模态参数辨识[21]。Verhargen[22]在1994年提出了PO-MOESP 算法(PO指past output),是MOESP 算法的一种变形,其思想是通过处理系统的输出矩阵方程,经过投影计算得出可观测矩阵的列空间,从而获得模态参数。Verdult 等[23]通过减小可观测矩阵的维数,减小了计算系统矩阵的工作量。然而,对于受到周期激励作用的结构,很难有效地辨识其高分辨率振型。邓先来等[22]利用一种无相移数字滤波器对响应信号进行处理,消除了周期激励对模态辨识的影响。董霄峰等[24]通过改进特征系统实现法(Eigensystem realization algorithm,ERA)与概率密度函数法(Probability density function,PDF)结合的运行模态识别方法,剔除了不同工况下叶轮和机组转频的谐波成分干扰。
对运行中的结构进行运行模态分析,需要准确测量在环境激励作用下的各个测点的响应[25]。本文研究一种在环境激励下基于周期性-过去输出多变量输出误差状态空间算法(Periodic PO-MOESP)的仅输出可测模态参数识别方法。相比其他算法,该方法可以同时处理过程噪声与测量噪声,在周期激励的作用下,可以准确识别出频率、阻尼和振型。通过有限元仿真得到结构在周期性激励作用下的位移响应信号,通过周期性采样构造Hankel 矩阵,基于Periodic PO-MOESP 算法对响应信号进行识别,得到可观矩阵,进而推导出系统矩阵并求解系统模态参数。采用一总长为60 m 的圆筒模型作为仿真算例,研究该算法的辨识精度和抗噪能力。最后将此算法应用于悬臂梁点模态试验,验证了该算法在周期激励下进行结构模态参数识别的有效性。
1 理论基础
1.1 Periodic PO-MOESP算法
运行中的风力涡轮机与停放的风力涡轮机在性质上是不同的,如同直升机和涡轮机等许多重要的系统,必须用线性时间-周期(LTP)运动方程来建模,以正确辨识风机模态参数[26]。
对于线性时间-周期系统,其状态空间方程描述如下:
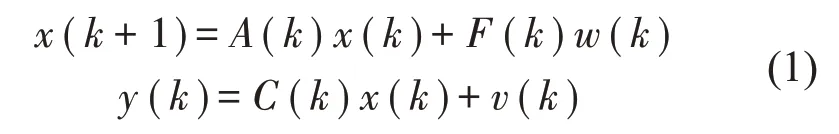
式中:x(k)为系统的状态变量矩阵,x(k)∈Rn;y(k)为系统的测量数据矩阵,由经数学处理后的观测信号组成,y(k)∈Rm;w(k)为输入的白噪声(过程噪声矩阵),均值为零;ν(k)为输出白噪声(测量噪声矩阵),均值为零;A(k)为系统状态传递矩阵;C(k)为输出传递矩阵。
矩阵A(k)、F(k)和C(k)都是离散周期为k的周期函数,为了把这个系统写成一种通常用于子空间的形式,定义了输出数组:
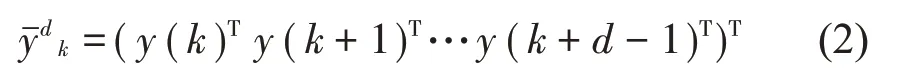
同样,过程噪声和测量噪声也是这样的数组。参数d为窗口大小,且P≥d>n。
LTP系统的可观测性矩阵被定义为
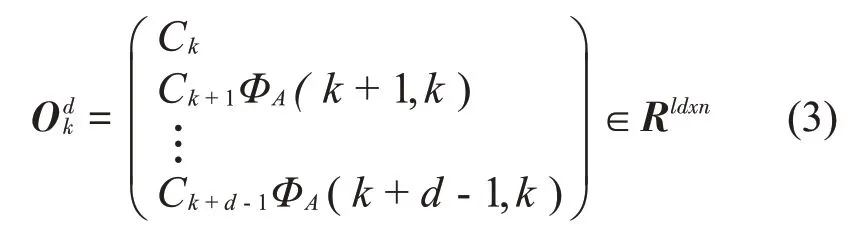
接下来假设系统对于所有k,除以长度d,都是可观测的,因此有满列秩,即rank(=n。定义:

=C(k+i-1)Φ(k+i-1,k+j)F(k+j-1),i=2,…,d;j=1,…,d-1并且i大于j。由于系统的周期性,可以证明和其中指周期的数量。根据这些定义我们可以得到:
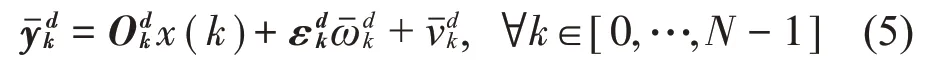

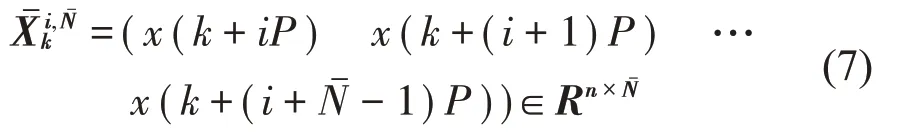
因此输出矩阵可以被记为
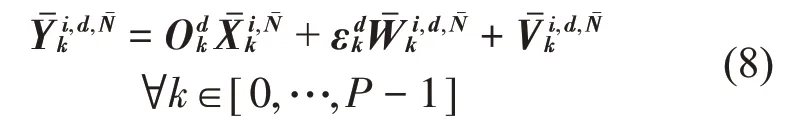
Periodic PO-MOESP 目的是利用数据矩阵来识别可观测矩阵。可证:
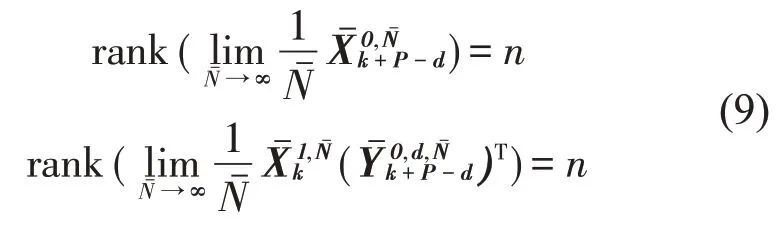
同时下式也成立:
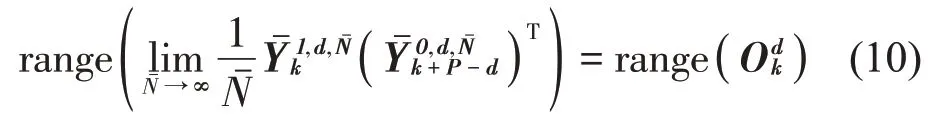
进行RQ分解:
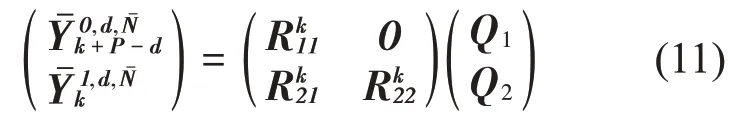
通过变换可以证明:
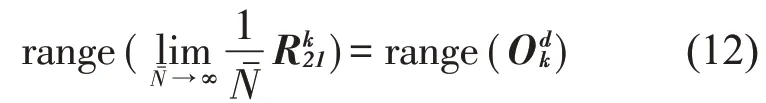
观测矩阵的值域可以通过计算的奇异值分解得到:
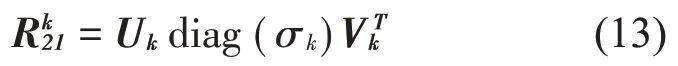
利用可观测矩阵的结构,取其前l行作为系统矩阵。矩阵Uk的i行到j行表示为Uk(i:j,:),因此输出矩阵表示为
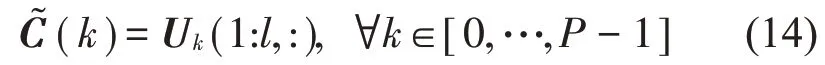
矩阵A(k)通过求解下列方程得到:
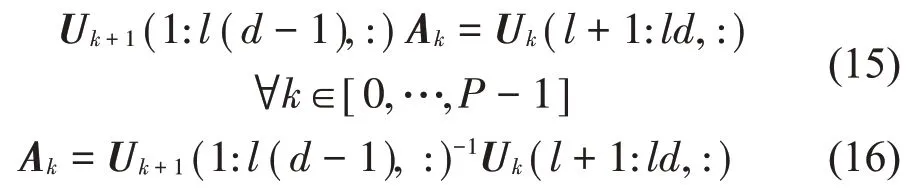
根据模态分析理论可知,求解矩阵A的特征值问题即可得到模态的固有频率和阻尼比[27]。当采用连续时间状态空间模型时,已知A的特征值λi和特征向量hi,固有频率、阻尼比及振型可由式(17)得到:
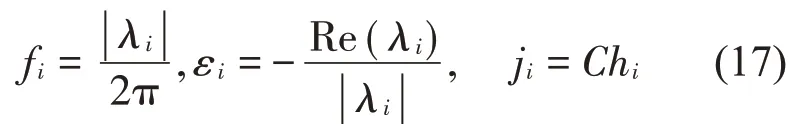
若采用离散时间状态空间模型,相应各阶模态的固有频率、阻尼比及振型为
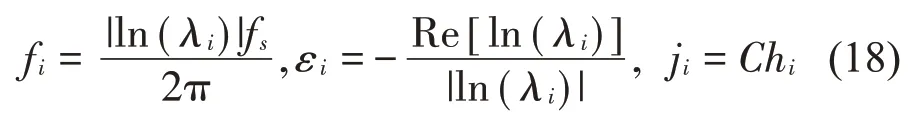
其中:fs为采样频率[28]。
1.2 算法实现步骤
(1)对结构施加激励并采集响应信号;
(2)利用位移响应信号构造Hankel矩阵;
(3)对Hankel矩阵进行QR分解得到R矩阵;
(4)对R矩阵中的R21按式(13)进行奇异值分解;
(5)通过扩展可观测性矩阵Odk求解A和C;
(6)求A的特征值得到模态固有频率fi、阻尼比εi;通过矩阵C求解模态振型。
图1为基于Periodic PO-MOESP算法的流程图。
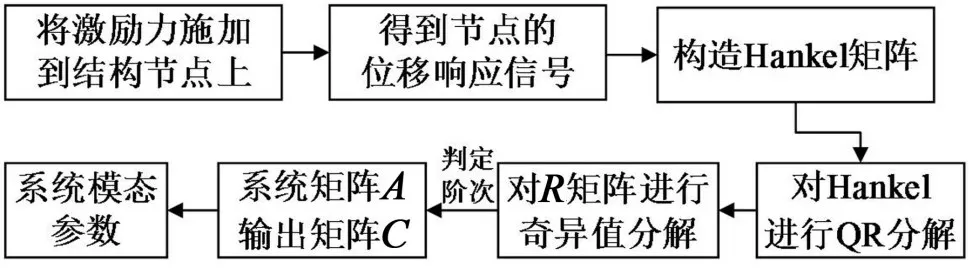
图1 周期力激励方法流程图
2 仿真算例
2.1 风机塔架模型
典型的三叶片风力机主要由旋转叶片、机箱、塔架、基座等部分组成,齿轮箱、传动机构、发电机和配电装置都安装在机箱中。到目前为止,风力机叶片长度最大可达100 米。叶片旋转时受到风载作用,使得整体结构所承受载荷呈现明显的周期性。塔架作为整个结构的支撑部件,振动对其的影响最为明显。因此,风机倒塌往往是由塔架的断裂引起的。风机塔筒模型结构及测点示意图如图2所示。
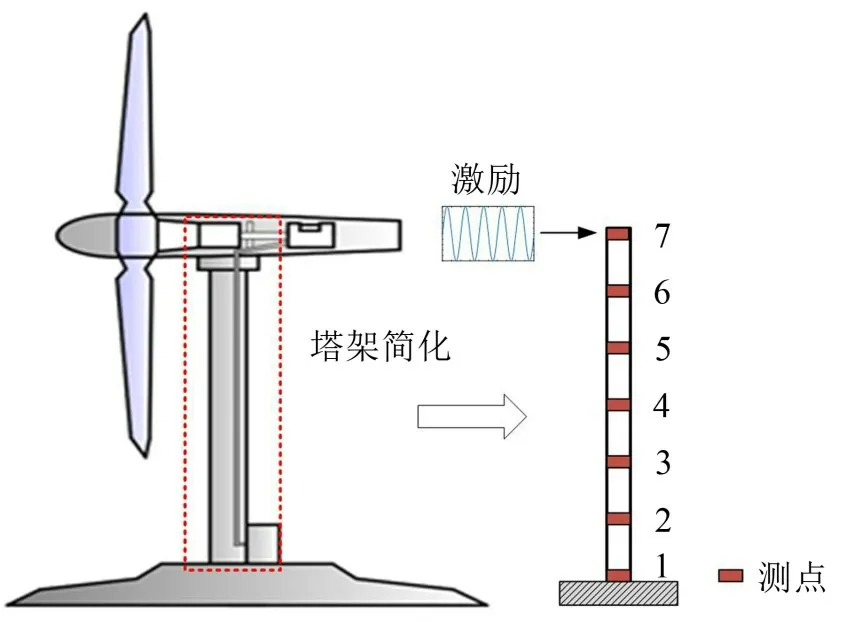
图2 风机整体结构示意图
本算例中将风力机整体结构进行简化,主要分析塔架的动态特性。以长度为60 m 的圆筒结构作为研究对象,外径为1.5 m,内径为1.4 m,沿长度方向等距设置7 个测点,测量相对根部的侧向位移。梁结构的有限元模型材料的弹性模量为2×105MPa,密度为7 850 kg/m3,泊松比为0.3,将测点1 固定作为边界条件。在实际风机模态辨识实验中,响应信号可通过加速度、速度和位移传感器进行测量。
通过有限元仿真软件对风机塔架有限元模型进行模态分析,计算得到结构模型前3 阶的模态参数作为参考值,如表1所示。

表1 塔架前3阶振动频率
为了验证Periodic PO-MOESP 算法的识别效果,现分别采用正弦信号激励和多频率谐波信号激励进行基于瞬态响应信号的结构动态特性分析。
2.2 基于正弦激励下的模态参数识别
本节以上述建立的风机塔架有限元模型为基础,给有限元模型的测点7 施加F=10 sin(40π×t)N的正弦激励力,激励力随时间的变化曲线如图3所示。图中所示为前5 s的激励信号,激励信号施加时间共为10 s。通过Periodic PO-MOESP 方法对结构7 个测点的位移响应信号进行模态参数识别,将识别的模态参数与有限元模型的理论计算值进行对比。
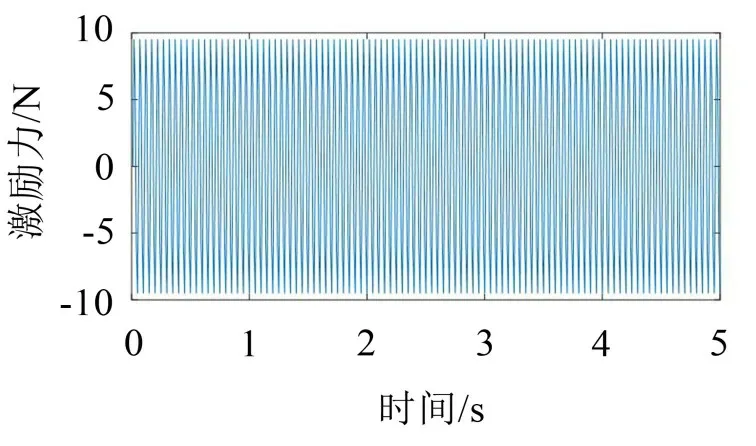
图3 正弦激励力随时间变化曲线
施加简谐激励力后,识别结果和仿真结果对比如表2所示。

表2 正弦激励下的识别结果与计算结果对比
分析可知,在测点7施加正弦激励后,可识别出结构的前3 阶频率和阻尼比。由对比结果可以得出,算法辨识结果与模态仿真结果的误差较小。
前3阶仿真模态振型与辨识模态振型的对比图如图4所示。
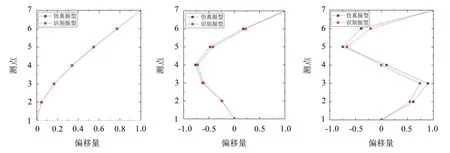
图4 前3阶结构振型对比图
由振型图对比结果可知,各阶模态振型的理论结果和识别结果比较接近,模态振型连续、准确,与精细有限元模态预分析结果具有相似的模态振型特征。将利用算法得到的结果与根据有限元仿真得到的振型结果的MAC 值对比,从图5 中可以看出,识别出的振型与有限元仿真得到的模态振型匹配度较高,模态置信度能达到0.98以上,表明该算法可以有效识别周期激励下的风机模态参数。
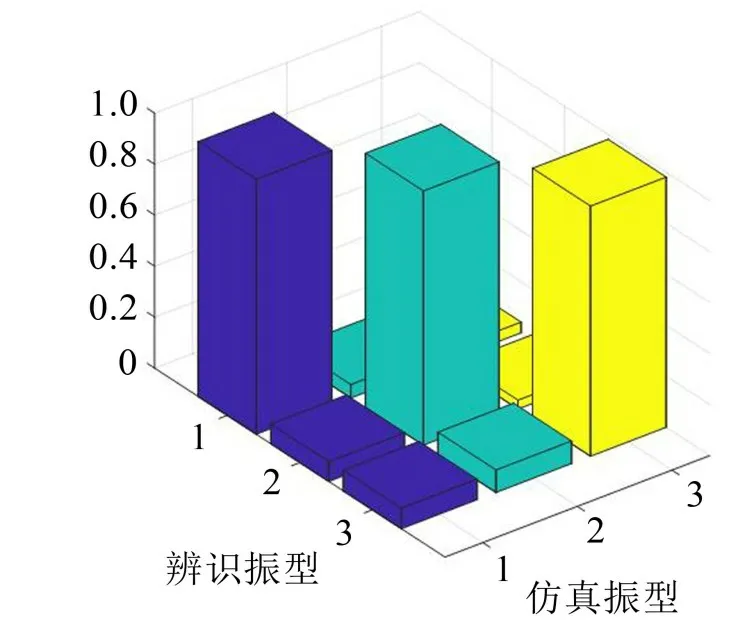
图5 识别振型与仿真振型MAC值对比
2.3 基于谐波激励下的模态参数识别
在实际运行过程中,当结构处于高转速状态时风力机会受到明显的叶轮倍频和谐波激励的作用,导致结构振动中的谐波成分占比较大,风机结构的模态频率与谐波成分较为接近,严重影响算法的识别精度。通过在不同时间段施加包含不同频率谐波成分的信号,模拟风机在实际运行过程中在不同风速下转子、叶片等结构旋转引起的周期激励。谐波激励力随时间变化曲线如图6所示。激励信号施加时间共为10 s,谐波成分为10 Hz、15 Hz、20 Hz的周期信号。
将图6的谐波输入信号作用在测点7上,保持采样频率、采样间隔与正弦激励时一致,采样频率为100 Hz,采样时间为10 s。通过瞬态响应分析得到7个测点的位移响应信号,数据总长为1 000。利用Periodic PO-MOESP 算法对输出的数据进行模态辨识,结构模态频率和阻尼特性的仿真结果和识别结果如表3所示。

表3 谐波激励下的识别结果与计算结果对比
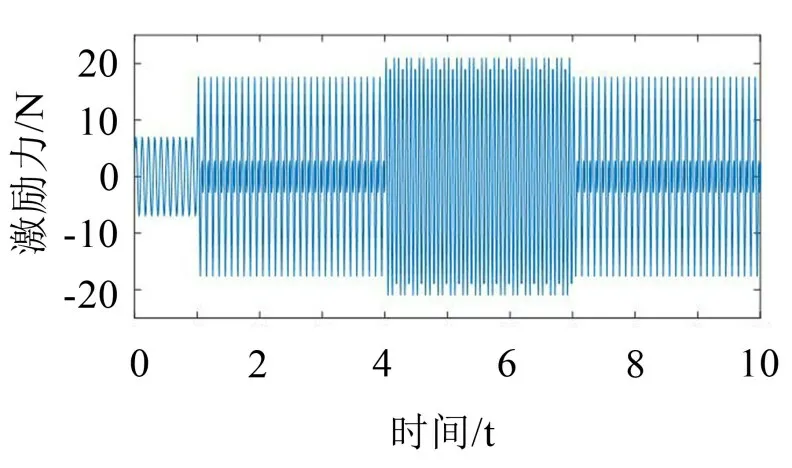
图6 谐波激励力随时间变化曲线
分析结果可知,在谐波激励的条件下,算法识别结果与有限元仿真结果吻合,通过辨识得到的前3阶频率和阻尼比的大小与仿真结果误差较小。前3阶仿真模态振型与辨识模态振型的对比如图7所示。
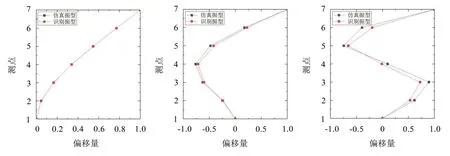
图7 前3阶结构振型对比图
由理论与识别结果对比可以看出,此算法在谐波激励力输入的条件下对模态的识别很准确。通过MAC值对比图8可以看出,识别振型与理论振型匹配度较高,模态置信度达到0.98以上。
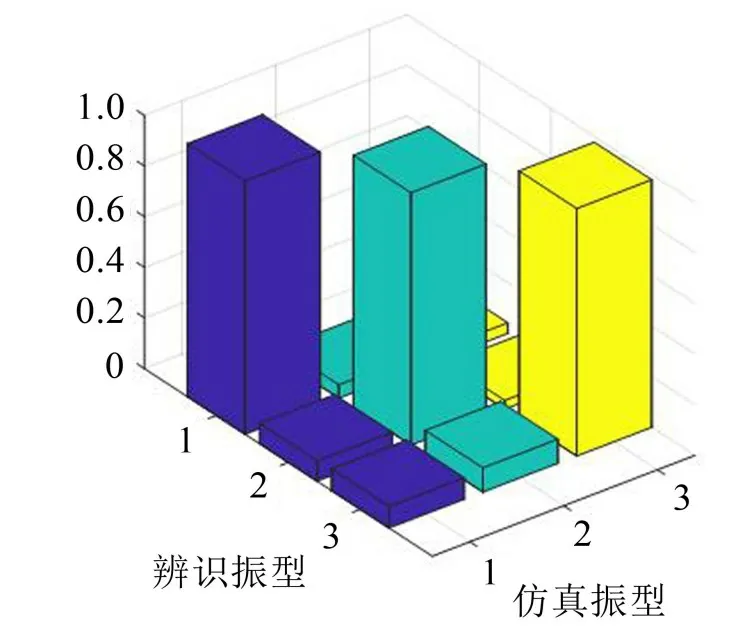
图8 谐波激励条件下辨识振型与仿真振型MAC值对比
2.4 抗噪性能
由于实际工程中不可避免存在噪声激励,本节研究5 %白噪声激励对模态辨识精度的影响以及Periodic PO-MOESP算法的抗噪性能。
将2.2节中正弦激励后得到的测点1至测点7的位移响应信号加入5%的白噪声,其中测点7响应数据加入白噪声后的信号前后对比如图9所示。将经过处理后的数据利用Periodic PO-MOESP算法进行模态辨识,得到如表4所示的结果。

图9 测点7响应数据加入5%白噪声后前后对比图

表4 加入5%白噪声激励后的识别结果与计算结果对比
分析结果可知,在谐波激励的条件下,算法识别结果与有限元仿真结果吻合,通过辨识得到的前3阶频率和阻尼比的大小与仿真结果误差较小。前3阶仿真模态振型与辨识模态振型的对比如图10所示。
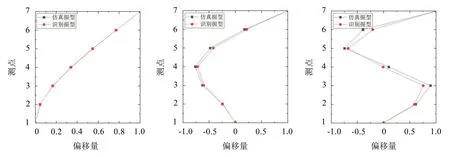
图10 前3阶结构振型对比图
将加入5%白噪声后利用算法所识别振型与根据有限元仿真得到的振型结果的MAC值对比,见图11,可知识别振型与仿真振型匹配度较高,模态置信度能达到0.98以上。说明加入5%白噪声后算法模态参数辨识精度较高,抗噪性能较好。
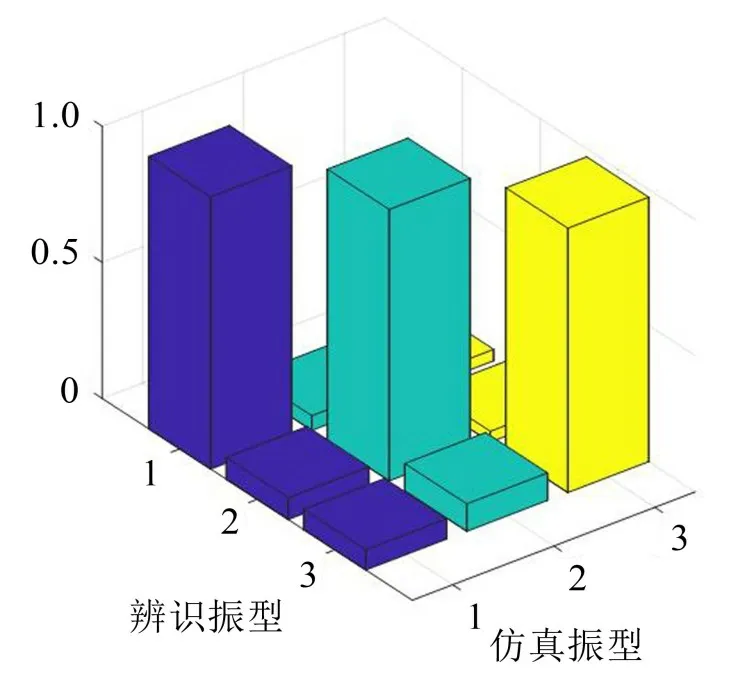
图11 识别振型与仿真振型MAC值对比
3 试验验证
以一端固支的柔性梁为试验件,利用激振器在梁顶部沿厚度方向施加周期激励。梁总长108 cm,截面宽度为3 cm,梁厚度为0.3 cm,采用和风机塔架相同的材料合金钢,其弹性模量为206 Gpa,泊松比为0.3,密度为7 850 kg/m3。从梁的底端开始,每隔20 cm布置一个电荷式单向加速度传感器,用以测量加速度响应信号。试验方案如图12 所示。试验件和装置如图13所示。
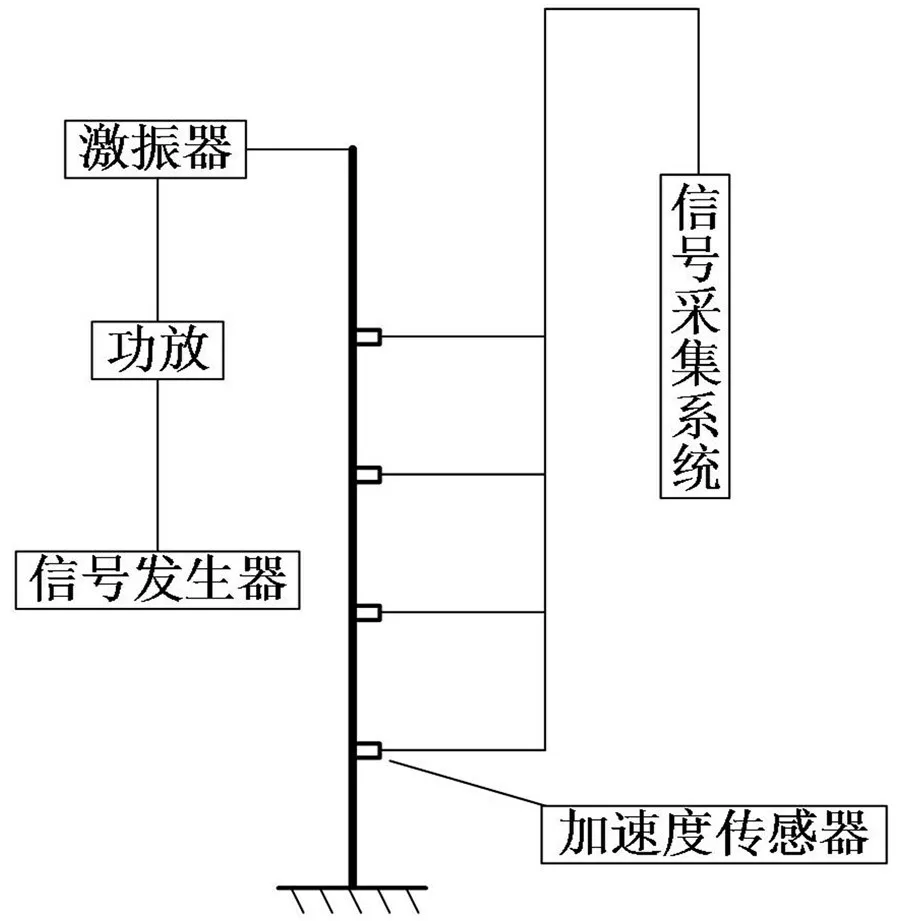
图12 试验方案原理图

图13 试验件和装置
梁结构底端通过夹具固定,激振器采用磁吸座固定。对试验结构施加40 Hz 的周期加速度信号,大小为1 g。采集加速度传感器的响应数据,采样频率为100 Hz,数据总长为20 000。通过东华DH5922D动态信号测试分析系统识别加速度信号,得到前3 阶频率试验值为1.369 Hz、7.860 Hz、21.284 Hz。利用本文算法对响应信号进行识别,得到的频率和阻尼识别结果与试验值的比较如表5和表6所示。
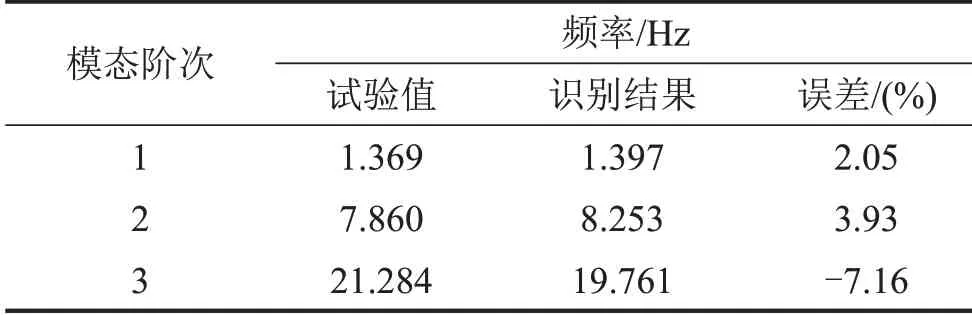
表5 频率识别结果与试验结果对比
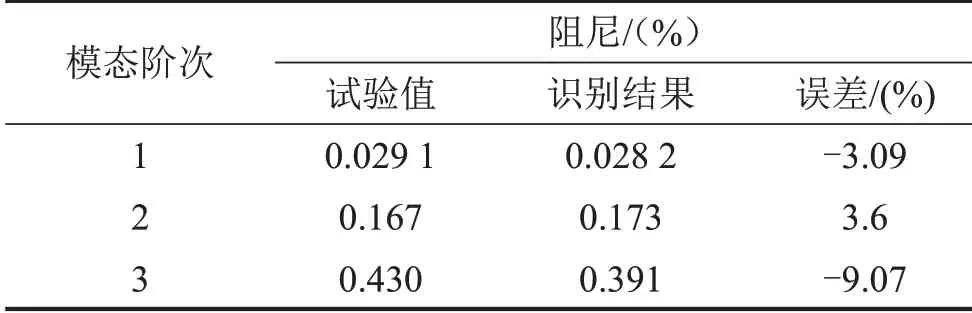
表6 阻尼识别结果与试验结果对比
由识别结果可知,采用本文算法识别梁结构模态参数精度较高,前3 阶频率识别结果与试验值的误差范围均在10%以内,1 阶频率误差为2.05%;2阶频率的误差为3.93%;3阶频率的误差为-7.16%。前3 阶模态振型与试验模态振型的对比如图14 所示。由识别与试验结果对比可以看出,此算法在周期激振的条件下对频率、阻尼和振型的识别都很准确。
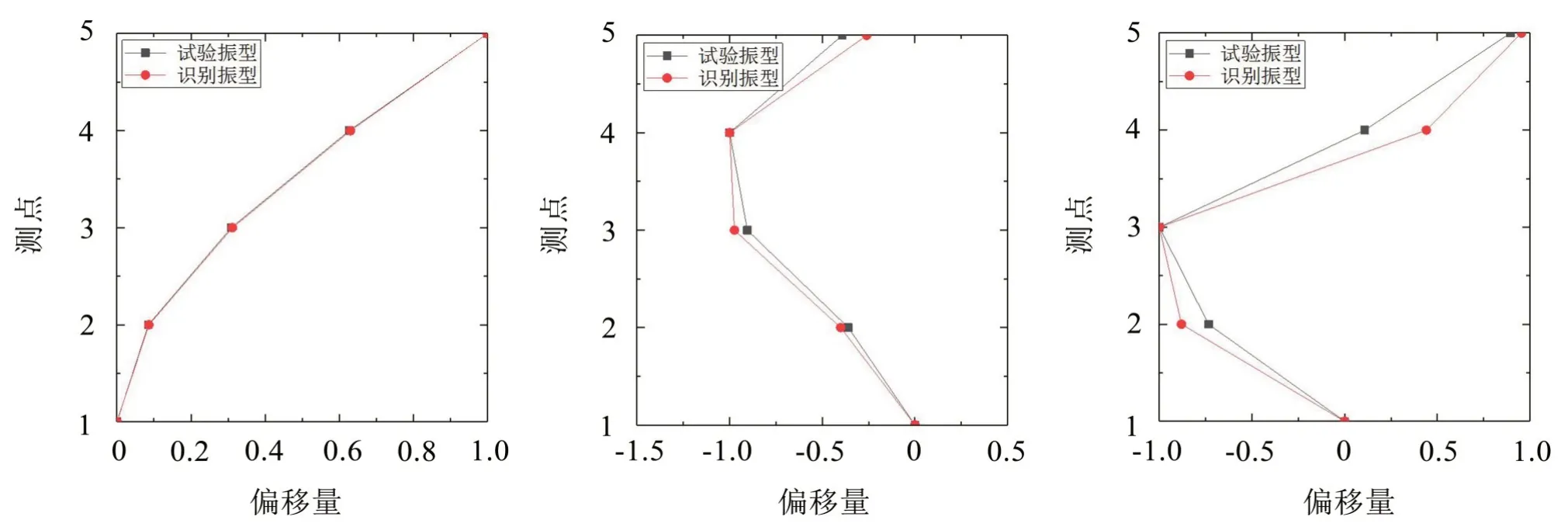
图14 前3阶结构振型对比
将基于本文算法识别得到的结果与采用动态信号测试分析系统得到的试验振型结果进行MAC 值对比,从图15 中可以看出,算法所识别振型与试验振型匹配度较高,模态置信度能达到0.96以上。
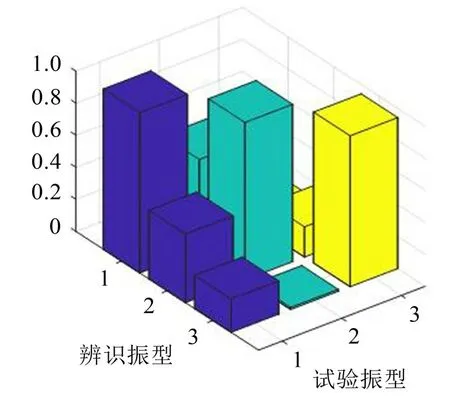
图15 试验振型与识别振型MAC值对比
4 结语
针对风力机运行模态试验中难以测得激励信号的问题,提出了一种仅需要位移输出信号的结构模态辨识方法。仿真算例中采用一60 m长圆筒结构,基于Periodic PO-MOESP算法对其进行模态参数识别,并将此识别结果和有限元正则模态分析结果进行对比。对比正弦激励和谐波激励下的模态参数辨识结果,结果显示不同周期激励的形式对该算法结构模态参数辨识的影响较小。在响应信号中加入白噪声,辨识结果证明该方法具有良好的抗噪性能。将此算法应用于一悬臂梁模态试验,验证了本文算法在周期激励条件下识别结构模态参数的有效性。

