桨-轴-船艉耦合系统分布式动力吸振器多频优化
蒋圣鹏,黄子祥,谢溪凌,张志谊
(1.上海交通大学机械系统与振动国家重点实验室,上海200240;2.上海交通大学振动、冲击、噪声研究所,上海200240)
水面舰船作为一个复杂的巨型噪声源,其水下辐射噪声主要来源于机械噪声、螺旋桨噪声和水动力噪声[1]。机械噪声随着船舶建造水平的提高和被动隔振技术、减振技术及阻尼吸振技术的广泛应用被显著抑制,在低航速时水动力噪声贡献并不明显,在高航速时又不如螺旋桨噪声显著,因此螺旋桨诱发的轴系-艉部耦合系统振动噪声逐渐成为舰船辐射噪声的主要因素。因此,降低由螺旋桨激励引起的桨-轴-船艉耦合系统振动十分重要[2]。
动力吸振器(Dynamic vibration absorber,DVA)又称调谐质量阻尼器(Tuned mass damper,TMD),是一种附加在主系统上用于振动控制的装置,其具有结构简单、成本低廉、不改变已有系统结构等特点,因此自1909年被Frahm发明以来,采用动力吸振器就被作为结构振动与噪声控制的主要方法之一。Den Hartog与Brockz在Hahnkamm定点理论的基础上推导的动力吸振器的最优调谐公式是动力吸振器优化设计的最经典方法,目前还有很多学者基于此方法进行动力吸振器的优化设计。Zhu 等[3]采用模态叠加法推导了含阻尼薄板基础模态与吸振器的振动响应,结合吸振器最优调谐公式,给出了分布式动力吸振器的解析优化公式,并针对前3 阶共振频率进行了吸振器的参数优化。刘哲等[4]针对艇体结构的低频线谱噪声,按照最优调谐频率比设计了分布式动力吸振器,该方法可使结构前2 阶共振峰值得到有效抑制。在进行多频控制时,基于最优调谐公式的吸振器优化方法只能分别求取系统单一频率的优化参数,再将该参数应用于多频联合控制,但是新吸振器的引入将会改变原系统振动特性,使基于原系统的吸振器最优参数不再最优。
除此之外,付江华等[5]将智能优化算法引入动力吸振器的优化设计中,比较了不同智能优化算法在进行吸振器参数优化时的优劣,但是该研究并未深入到复杂系统的多频优化。王名等[6]针对薄壁件铣削过程中的振动控制问题,利用ANSYS Workbench中的目标驱动优化算法对分布式动力吸振器进行了参数优化,可使零件频响函数幅值下降85%以上,但是当系统复杂度升高,有限元网格较多时,该方法的时间成本将会很高。
本文采用分布式动力吸振器对螺旋桨激励下的桨-轴-船艉耦合系统进行多频振动控制。首先采用有限元法计算系统耦合振动特性,根据系统模态振型确定吸振器位置与数量。提出了基于遗传算法的分布式动力吸振器多频优化方法,以吸振器刚度和阻尼为优化变量、以艉部船体均方振速为目标函数,计算得到吸振器最优参数。同时为了缩短计算时间,引入频响综合法求取吸振器作用下桨-轴-船艉系统的耦合振动响应。
1 桨-轴-船艉耦合系统振动特性
桨-轴-船艉耦合系统由艉部船体、螺旋桨和轴系组成,其几何模型如图1 所示。船体总体尺寸约为70 m×20 m×12 m,由多层甲板、横舱壁、前后艉轴架等结构组成;螺旋桨为5叶桨,直径为4 m,总重量约为6 t;轴系长50 m,直径约为0.3 m,通过后艉轴承、前艉轴承、艉管水润滑轴承、中间轴承和推力轴承与艉部船体耦合。系统模态频率与振型如图2所示。其中2.7 Hz 和8.2 Hz 对应船体艉部弯曲模态,10.8 Hz 和13.6 Hz 对应轴系弯曲模态,16.9 Hz 和25.9 Hz对应桨-轴-船艉系统耦合模态。
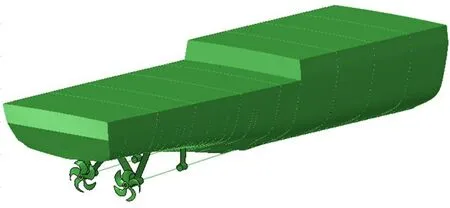
图1 桨-轴-船艉耦合系统几何模型

图2 桨-轴-船艉耦合系统典型模态
在螺旋桨位置施加垂向激励,计算桨-轴-船艉耦合系统各点的振动速度响应,得到艉部壳体均方振速如图3 所示。在螺旋桨垂向激励下,艉部壳体在低频段振动响应较大,本文针对桨-轴-船艉耦合系统低频段艉部壳体响应较大的问题,设计动力吸振器对其进行振动控制。

图3 桨-轴-船艉耦合系统艉部船体均方振速
2 吸振器位置与质量的确定
吸振器的安装位置对吸振效果影响很大,若吸振器安装在模态节点上,那么不论吸振器参数如何选取,都不会产生任何减振效果;若吸振器安装在振动响应较小的位置,那么该点的等效质量将会很大,对应的吸振器质量也会很大。所以一般而言,吸振器应该安装在系统位移响应较大的位置。
由桨-轴-船艉耦合系统前5阶振动峰值可知,频率为2.7 Hz与8.2 Hz时模态振型振动较大位置为船体艉部,因此将动力吸振器安装在船体艉部甲板上(图4 中A 区),数量为8 个;频率为16.90 Hz 和25.95 Hz时激励力经轴系传递至艉部壳体,而后艉轴承为主要传递路径,因此将吸振器分布安装于后艉轴架上方甲板上(图4中B区),数量为8个。
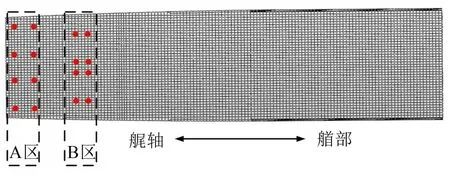
图4 吸振器安装位置
此外,动力吸振器吸振效果与质量比μ密切相关,质量比越大,动力吸振器吸振效果越好,但是动力吸振器的质量一方面会受安装条件的限制,另一方面过大的质量会影响主系统的振动特性,使系统固有频率前移。研究表明,当质量比μ超过0.2 时,随着质量比的升高,动力吸振器的减振效果提升速度将变缓,质量比对减振效果的影响灵敏度将会降低[8]。因此,综合考虑结构模态质量和安装尺寸要求,选定吸振器质量为500 kg。
3 系统响应计算
若桨-轴-船艉耦合系统响应点个数为L,安装动力吸振器个数为M,系统外激励力个数为N,则振动响应函数可写为

式中 :Xi为响应点位移响应 ,Xi=[xi1xi2… xiL]T;Xj为动力吸振器安装点位移响应,Xj=[xj1xj2… xjM]T;Hii和Hji为系统激励下的位移导纳,分别为L×N和L×M阶矩阵;Hij和Hjj为动力吸振器激励下的位移导纳,分别为M×N和M×M阶矩阵;Fi为系统外激励力,Fi=[fi1fi2… fiN]T;Fj为动力吸振器对系统的激励力,Fj=[fj1fj2… fjM]T。
分别在fin(n=1,2,…,N)处激励系统,其余位置不提供激励力,得到系统激励下的位移导纳Hii=Xi/Fi,Hji=Xj/Fi;分别在fjm(m=1,2,…,M)处激励系统,其余位置不提供激励力,得到系统激励下的位移导纳Hij=Xi/Fj,Hjj=Xj/Fj。
对于第r个动力吸振器,其动力学方程为
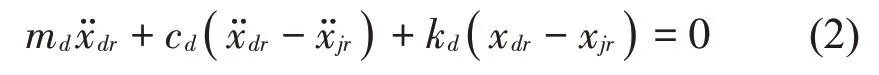
对式(2)进行拉氏变换后计算吸振器对系统的激励力fjr为

记A={A1,A2,…,AM},则可将式(3)整合为

将式(4)代入式(1)中,化简后可得:

桨-轴-船艉耦合系统均方振速和均方振速级可由系统位移响应计算[7]:

式中:v0为速度参考值,v0=1×10-9m/s。
采用能量叠加法将不同频率下矩形薄板的均方振速级转化为振动速度总级LT:

式中:K为频率点总数;Lvi为第i个频率点的均方振速级。
在已知系统位移导纳和动力吸振器参数的情况下,通过式(5)就可以求出系统激励力作用下安装动力吸振器后桨-轴-船艉耦合系统的振动响应情况。其中系统激励下的位移导纳Hii和Hji以及动力吸振器激励下的位移导纳Hij和Hjj只与系统结构有关,只要系统确定便不会改变;动力吸振器传递矩阵A只与吸振器参数有关,在吸振器参数优化过程中,只需计算不同参数下的矩阵A即可。
一般而言,系统导纳矩阵可通过解析法或有限元法求得。桨-轴-船艉耦合系统结构复杂,解析模型通常难以建立,解析解也难以求取,因此本文通过有限元法获取桨-轴-船艉耦合系统位移导纳。
4 动力吸振器参数优化
4.1 基于遗传算法的动力吸振器优化方法
在得到动力吸振器位置和质量的基础上,需要对吸振器的刚度和阻尼进行优化计算,常见的优化方法可分为两类:经典优化算法和智能优化算法。智能优化算法相对于经典优化算法而言,更利于处理多变量、多峰值的复杂工程问题,常见的智能优化算法有粒子群算法、蚁群算法、遗传算法等。其中,遗传算法相比于其他智能优化算法,对多模型、多目标的函数优化问题的求解易于得到较好的优化效果,因此本文采用遗传算法进行动力吸振器的优化设计。
遗传算法以一个种群的所有个体为研究对象,利用交叉变异产生子代,并通过适应度控制个体遗传概率,最终通过层层迭代,获得适应度高的最优个体。桨-轴-船艉耦合系统动力吸振器优化问题的优化变量为吸振器刚度和阻尼,目标函数为指定频段(f0,ft)内系统均方振速的有效值:
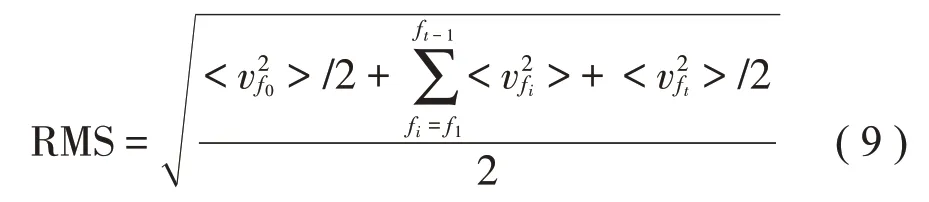
将目标函数RMS转化为适应度函数:

因此桨-轴-船艉耦合系统动力吸振器优化问题可描述为

遗传算法相关参数如表1 所示。具体步骤如下:

表1 算法参数
(1)设定算法最大迭代次数、种群大小、变量边界、变量离散精度等参数,采用二进制编码法随机产生初始种群。
(2)判断种群是否符合算法终止准则,若符合,则输出当前种群的最优个体和其对应的最优解,算法终止,若不符合,则转向(3)。
(3)以个体适应度为基础,采用轮盘赌法确定每个父代个体将自身基因遗传给子代的概率,选择适应度高的个体参与遗传操作,适应度低的个体被淘汰。
(4)对个体进行复制、交叉或变异操作,产生子代个体,子代个体的集合组成新种群。同时为提高算法收敛速度,将每一代中的最优个体直接复制到其子代。
(5)对新种群重复(2)操作,直至满足算法终止准则。
4.2 单频优化
针对桨-轴-船艉耦合系统2.7 Hz、8.1 Hz、16.9 Hz 和25.9 Hz 频率处的振动响应,分别对单一频率下的动力吸振器参数进行优化计算。优化结果如表2所示。吸振前后对比如图5所示。

表2 桨-轴-船艉耦合系统单频优化吸振器最优参数

图5 单频优化下艉部船体均方振速级
结果表明,采用基于遗传算法的分布式动力吸振器优化方法进行单频优化,计算得到的吸振器可减少耦合系统共振峰幅值7 dB以上,25.9 Hz处共振峰幅值甚至降低了16.6 dB,说明将优化方法应用于桨-轴-船艉耦合系统单一频率吸振具有良好效果。
将表2中根据单频优化得到的动力吸振器参数进行桨-轴-船艉耦合系统多频振动控制,得到的控制效果如图6所示。对比图5发现,使用单频优化参数对系统多个共振峰进行控制时,控制效果并不理想,在2.7 Hz 处甚至出现了振动响应变大的情况。说明在引入不同频率的吸振器后,系统振动特性发生了变化,使原来2.7 Hz 频率下的单频优化参数不再最优,进而导致吸振效果变差。这种情况下,需要同时考虑不同频率下的吸振器对系统的影响,进行桨-轴-船艉耦合系统的多频全局优化。

图6 根据单频优化参数联合控制下艉部船体均方振速级
4.3 多频优化
将不同频率下的吸振器参数同时纳入优化算法的优化变量中,进行桨-轴-船艉耦合系统动力吸振器多频参数优化。优化变量数量为8,目标函数同样为系统均方振速有效值,得到吸振器最优参数如表3所示。对应频响曲线如图7所示。在进行多频同时吸振时,多频优化算法考虑了不同吸振器对系统的耦合影响,因此得到的吸振器最优参数能起到比单频优化参数更好的效果,尤其在2.7 Hz和25.9 Hz频率处吸振效果相比图6得到明显改善。

表3 桨-轴-船艉耦合系统多频优化吸振器最优参数
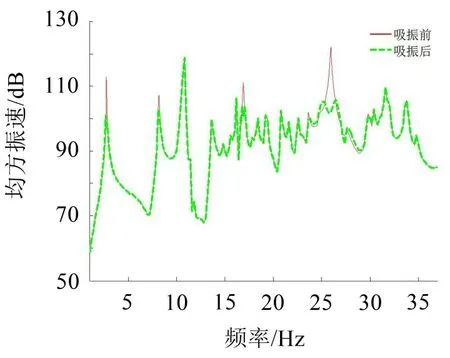
图7 多频优化参数下艉部船体均方振速级
但是将吸振器布置在后艉轴架上方甲板上的方案无法对10.8 Hz 处的共振峰进行有效抑制。这是因为10.8 Hz对应轴系弯曲模态,在螺旋桨垂向激励下后艉轴承不是振动的主要传递路径。
5 结语
(1)采用本文提出的基于遗传算法的分布式动力吸振器多频优化方法计算得到的分布式动力吸振器可有效抑制螺旋桨垂向激励向船体的传递,进而降低艉部船体表面法向振动,使艉部船体法向均方振速下降7 dB以上。
(2)采用单频优化参数的分布式动力吸振器进行多频优化时,由于原系统振动特性受到不同吸振器的影响,吸振器效果变差,需要同时考虑不同吸振器对原系统振动特性的影响。
(3)本文提出的分布式动力吸振器多频优化方法解决了单频优化参数应用于多频优化时效果变差的问题。基于多频优化得到的吸振器可降低艉部船体法向均方振速6 dB以上。
(4)采用频响综合法计算动力吸振器作用下艉部船体振动响应,可大大减少遗传算法的优化时间。

