绝热层缠绕成型纠偏方法与控制研究

肖扬 侯增选 严文聪 张伟超 邱传森

摘要：研究了固體火箭发动机绝热层缠绕成型过程中胶带跑偏问题，设计了相应的纠偏控制方法。首先分析了缠绕成型过程中胶带跑偏的原因，提出了相应的纠偏方案和控制系统。分析了控制系统的硬件组成，并结合纠偏方案建立了完整的纠偏控制系统数学模型。基于该模型设计了电流环、转速环和整体位置环的三闭环纠偏控制策略并进行了仿真验证。其中电机内的电流环和转速环采用 PI 控制;在内环设计基础上，整体位置环采用模糊自整定 PID 控制，通过设计算法动态调整 PID 参数。Simulink仿真结果表明，电流环能够将超调抑制在4.61%，转速环调节时间短（0.015 s），两环的动态性能良好，且无稳态误差。通过与 PID控制对比，模糊自整定 PID控制的响应曲线抑制超调能力明显（3.00%），调节速度快（0.367 s），且曲线过渡光滑，这表明纠偏效果要优于 PID 控制。关键词：绝热层;缠绕成型;纠偏方案;控制系统;PI ;模糊自整定 PID

中图分类号：TB3             文献标志码：A

文章编号：1009-9492（2021）12-0045-05                          开放科学（资源服务）标识码（OSID）：

Research on Rectification Control Method of Winding Molding of Heat Insulation

Xiao Yang1，Hou Zengxuan1※，Yan Wencong2，Zhang Weichao1，Qiu Chuansen1

（1.School of Mechanical Engineering， Dalian University of Technology， Dalian， Liaoning 116024， China;

2.Xi′an Aerospace Composites Research Institute， Xi′an 710025， China）

Abstract： A corresponding rectification control method was designed for the problem of the deviation of the tape position during the winding molding of heat insulation of solid rocket motor. First， the reasons for the deviation of the tape during the winding molding were analyzed， and the rectification scheme and control system were proposed. The hardware composition of the control system was analyzed， and a complete mathematical model of the rectification control system was established based on the rectification scheme. Based on the model， a three-closed loop rectification control strategy including current loop， speed loop and overall position loop was designed and verified by simulation. The current loop and speed loop in the motor adopted PI control to realize steady-state errors adjustment， based on the inner loop design， the overall position loop adopted Fuzzy self-tuning PID control， and the PID parameters were dynamically adjusted through the design algorithm. Simulink results show that the current loop can suppress the overshoot to 4.61%， the speed loop adjustment time is short （0.015 s） ， the dynamic performance of the two loops is good， and there is no steady-state error. Compared with PID control， the response curve of Fuzzy self-tuning PID control has obvious overshooting ability （3.00%） ， fast adjustment speed （0.367 s） ， and smooth curve transition， whichshows that the rectification effect is better than PID control.

Key words： heat insulation; winding molding; rectification scheme; control system; PI; Fuzzy self-tuning PID

0 引言

固体火箭发动机是一种性能优越的火箭动力装置，为了保证发动机壳体在运行过程中的稳定性，需要在壳体内衬一层绝热层，用于隔离固体燃料和壳体，因此绝热层的成型质量非常重要。目前国内主要采用人工贴片的方法实现绝热层成型，劳动强度大、效率低、且成型质量稳定性差，因此急需开展绝热层缠绕成型工艺的研究[1]。

在缠绕成型过程中，胶带需要按照预定轨迹由压辊缠绕到芯模表面，但在实际运行当中，受各类干扰因素的影响，胶带不可避免地会发生跑偏[2]。胶带跑偏会使绝热层局部材料堆叠或漏缝，降低绝热层成型质量;跑偏严重时，胶带可能脱离压辊，逼停缠绕过程。因此在缠绕过程中必须进行缠绕胶带纠偏，保证胶带缠绕位置准确。王志辉等[3]针对壳体纤维缠绕提出了模糊 PID 复合控制方案，但并未进行详细的方案设计与验证。杨开平等[4]针对复合材料缠绕工艺，在建模基础上对纠偏控制系统的稳定性进行分析并设计了智能算法，但其仿真模型过于简化，可靠性不高。何晓东等[5]针对复合材料缠绕过程，分析了双辊纠偏的传动特性，并与 PID 控制对比验证了模糊纠偏策略的优越性，但是其纠偏动作缓慢，时间过长。

本文首先分析绝热层缠绕过程中胶带跑偏的原因，并进行了纠偏方案的设计。其次建立了完整的纠偏控制系统的数学模型，并基于电机模型设计了双闭环调速系统的 PI 控制。最后基于整體模型设计了模糊自整定 PID 控制策略，利用模糊算法调整 PID 参数，并进行了 Simu? link仿真验证。

1 缠绕胶带跑偏原因分析

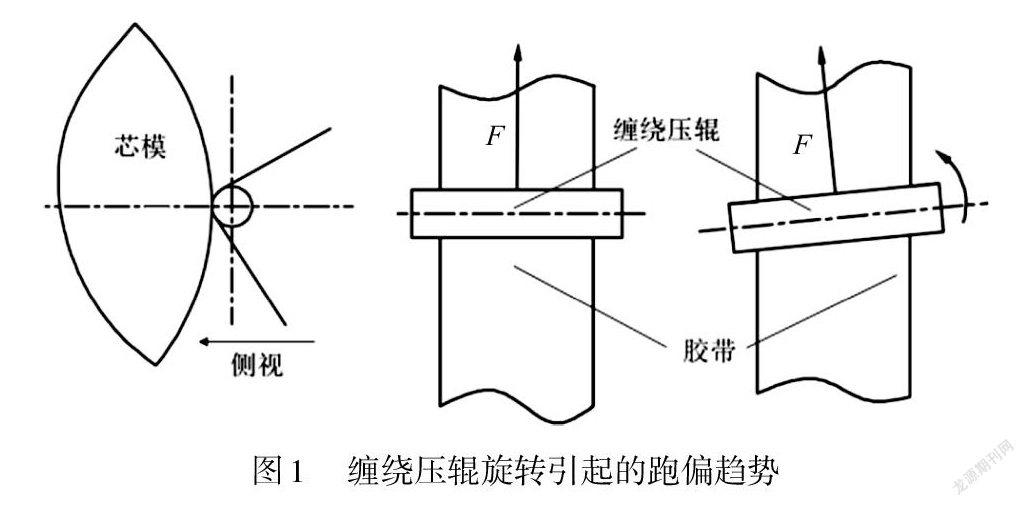
如图1所示，当采用环向缠绕方法时，缠绕压辊需旋转给定缠绕角，缠绕压辊对胶带产生一个横向作用分力，从而导致胶带横向跑偏趋势。

除压辊姿态影响外，胶带在运行过程中同样会受到胶带断面不均匀、导向辊的几何形状及安装误差、胶带盘不规则和自动化缠绕过程中胶带运动、振动等跑偏因素的影响[6]。因此，在固体火箭发动机绝热层缠绕成型过程中必须对胶带跑偏趋势进行抑制，并对跑偏胶带进行纠偏。

2 纠偏方案设计

纠偏方案如图2所示，纠偏辊安装在缠绕压辊上方。第一步，缠绕开始时，缠绕压辊旋转给定的缠绕角，为抑制胶带跑偏趋势，在缠绕压辊旋转给定的缠绕角时，同步控制纠偏辊反方向旋转相应角度。第二步，其他原因引起的胶带跑偏，通过红外传感器实时检测胶带偏移情况，计算胶带位置偏差信息，在原有纠偏角度基础上对纠偏辊旋转角度进行微调，保证胶带缠绕位置。微调过程由自动纠偏控制系统实现。

如图3所示，自动控制纠偏系统由传感器、控制器、电机和传动机构组成。在本控制系统中，选择利用 RLK-168红外传感器检测胶带位置，该传感器采用入射式结构，占用空间小，适用于空间局促的缠绕头部。控制器选择 STM32单片机，作为自动纠偏控制系统的核心，实现信号的处理和传递。直流电机具启动性能良好、大范围内调速平滑、可靠性高且易于控制的优点，适用于动作频繁，跟随性能要求高的纠偏控制，因此选择利用直流电机和蜗轮蜗杆组成传动机构[7]。

3 纠偏控制系统模型

纠偏控制系统的原理如图4所示，利用红外传感器实时检测胶带实际位置，并与基准位置比较，当检测到偏移量超过允许范围时，单片机输出控制指令驱动直流电机转动，带动蜗轮蜗杆和纠偏辊，令胶带位置回正，构成闭环位置控制系统[8]。

根据纠偏原理，为了保证纠偏控制系统的性能，既需要保证纠偏各环节的精度足够高，也需要纠偏控制算法的性能够优良。因此需要针对纠偏过程设计相应的控制算法。验证纠偏算法的功能性，首先需要建立纠偏控制整体的数学模型。数学模型的主要环节包括传感器、直流电机、蜗轮蜗杆和纠偏辊。

（1） 传感器

RLK-168红外传感器，结构紧凑且灵敏度高。采用边缘检测的测量方式，传感器安装方向垂直于胶带运行方向，这样检测到的跑偏量与输出模拟电压量呈正比，可得该环节的传递函数为：

（2） 直流电机

直流电机采用 PWM 变换器，通过改变占空比进行调压调速，PWM 输出平均电压与单片机的输出电压呈正比，且其响应延迟时间不超过一个开关周期[9]，由此可得：

直流电机电压驱动回路的方程为：

经过拉普拉斯变换可得：

式中： Tl = L/R ，为电机驱动回路的电气时间常数。

又根据转矩平衡方程，可得电磁转矩与电驱电流成正比：

同理可得负载转矩与对应电流的转矩计算公式为：

输出转矩与电机转速间的关系为：

又根据电磁感应定律：

综合式（5）～ （8） 并进行拉氏变换后可得电流与电感之间的关系式为：

结合式（4）、（8） 和（9） 可得直流电机的动态模型如图5所示。

选用直流电机相关参数如表1所示。

（3） 蜗轮蜗杆

传动机构采用蜗轮蜗杆，其输入转速与输出转速之间的比值为传动比，而输出转角与输出转速之间为积分关系，因此可得输入转速与输出转角之间的模型为：

（4） 纠偏辊

由于纠偏辊转动角度很小，在小范围内可将纠偏辊转动角度与纠偏量近似为比例关系，即 y = l sin θ≈lθ，由此可得纠偏辊与转动角度之间的动态模型为：

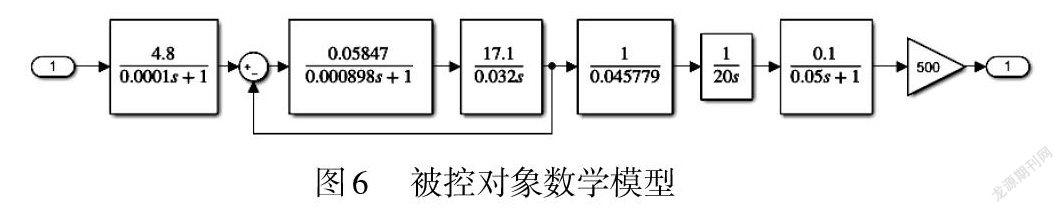
Simulink 是 Matlab 内的可视化仿真工具，具有丰富强大的模块库，因此非常适用于动态系统的建模和仿真[10]。因此，选择在 Smimulik中建立数学模型并进行相应的算法验证。根据上述分析后可建立未加控制的被控对象模型如图6所示。根据图中各环节公式可以看出，纠偏系统本身包含多个积分和惯性环节，在不加控制器的情况下，输出会非常不稳定。接下来根据该模型设计相应的算法并进行仿真验证。

由于跑偏信号的复杂多变，参数固定的 PID 控制并不能取得理想的控制效果。如果能够通过模糊算法实时调整 PID 参数，可达到更佳的控制效果。因此选择利用模糊自整定 PID 策略控制自动纠偏系统。而电机内环（电流环和速度环）利用 PI 算法进行整定，保证输出转速的稳定。三环调整顺序由内而外，依次为电流环、速度环和整体位置环[11]。

4 纠偏控制策略仿真

4.1 内环控制

利用PI算法设计电流环和转速环，调整电流环，能够抑制电流超调量，提高控制电流的稳定性，在电流环的基础上调整转速环，可以提高转速响应速度，实现无静差调速[12]。根据工程整定方法，可得如图7所示电机闭环系统。

其中電流环ACR和转速环ASR调节器的算法公式为：

将图7中所示双闭环直流电机模型封装成块并命名为“Motor Function”，便于与其他模块连接。

分别给入电流环和转速环单位阶跃信号，响应曲线如图8～9所示。由于积分环节的存在，响应曲线均无稳态误差。电流环超调量为4.61%，稳态值为0.28 A ，进入误差带1%的调节时间为1.61×10-3 s ，电流环的 PI 控制对于超调的抑制作用明显，且响应速度快，表明电流变化对输出转速的干扰小。

如图9所示，转速环响应曲线的超调量为38.8%，稳态值为71.43 rad/s ，进入误差带1%的调节时间 Ts=0.015 s ，无明显振荡，稳定性和快速性良好。

4.2 外环控制

外环采用模糊自整定 PID 方法进行调整，在已调试好的 PID 参数基础上，根据跑偏量的实时情况进行参数调整，其数学关系如下：

式中： kp 为实时调整参数; kp0为初始参数;Δkp 为模糊整定输出值，其余两式同理。经过参数整定， kp0 、 ki0和 kd0分别为0.40、0.70和0.02。

在 Matlab内调用“fuzzy”命令打开模糊控制器工具箱，编译界面如图10左。考虑到兼顾模糊控制的精确性和运算复杂程度，设计以二维变量 e 和 ec 作为输入， kp 、ki 、kd 的整定量为输出的两输入三输出控制器[13]。其得到的模糊变量 e 和 ec 分均取值[-1.5， 1.5] mm 和[-15，15]mm/s ，Δkp  、Δki  和Δkd  的变量范围取[-0.045，0.045]，[-0.3，0.3]，[-0.015，0.015]。取模糊工具箱内编译变量范围为[-3，3]，则比例和量化因子分别为2、0.2、0.015、0.1和0.005。输入输出各变量对应的模糊子集均划分为{NB ，NM ，NS ，ZE ，PS ，PM ，PB}，隶属函数以三角函数为主，考虑到函数分布的完备性、一致性和交互性[14]，结合经验可得函数分布如图10所示。

在编译模糊规则时，首先应依据如下原则：（1） 当偏差 e 偏离稳定值很大的时候，考虑到加快响应速度，应该选择较大的 kp ; （2） 当偏差 e 和偏差变化量 ec 都为中等的时候，选择较小的 kp 和适当的 kd  ，减小超调量;（3）当偏差比较小时，选择较小的 kp 和较大的 ki ，提高系统的稳定性;（4）如果偏差变化量比较大，那么应该减小 kp ，增大Δki 。

基于上述调整原则，结合控制经验和多次调试后，整理出如表2～4编译规则。

在 Simulink中建立如下PID 控制与模糊 PID 控制模块并分别封装并命名为“Fuzzy -pid”和“pid”，分别控制纠偏系统模型，通过观测窗口可得曲线对比，仿真控制系统如图11所示。

4.3 仿真结果对比

分别对整体位置环利用 PID 算法和模糊 PID 算法仿真模型输入相同的阶跃信号，仿真时间取2 s ，可得到如图12所示的响应曲线。

根据响应曲线对比可得， PID 控制下的超调量为12.7%，调整时间为0.584 s ，且有明显的振荡过渡。模糊自整定控制下的超调量为3.00%，调整时间0.367 s，且曲线过渡光滑，无振荡。通过对比可以明显看出，模糊 PID 算法抑制超调的能力更为优秀，调增时间更短，且没有振荡，稳定性和快速性均优于 PID 控制，因此可以认为模糊 PID 算法的响应态势更为良好，更加适合作为纠偏控制策略。

5 结束语

本文首先分析了缠绕压辊姿态对于胶带跑偏的影响，其次设计了纠偏方案，保证能够及时抑制纠偏趋势且实时微调。分析了自动纠偏控制系统的原理，并建立了其各环节的数学模型，最后设计了纠偏控制策略，电机的电流环和转速环采用 PI 控制，抑制了电流环超调，实现了电机无静差调速;纠偏系统采用模糊自整定 PID 控制，Simulink仿真结果表明，能够快速稳定实现纠偏动作，无振荡、超调小、调节速度快。同理，该策略同样可以供纸张、薄膜等带材的纠偏控制借鉴。

参考文献：

[1]赵有航.固体火箭发动机绝热层自动缠绕成型轨迹规划[D].大连：大连理工大学，2020.

[2]阎龙， 江伟， 史耀耀.复合材料布带缠绕纠偏控制系统设计[J].宇航学报，2012，33（8）：1171-1176.

[3]王志辉，乔海洋， 陈宏娟.纤维带缠绕智能纠偏控制系统设计与仿真[J].机电工程技术，2005（11）：36-38.

[4]杨开平， 史耀耀，何晓东，等.复合材料布带缠绕智能纠偏控制技术[J].航空学报，2011，32（7）：1318-1325.

[5]何晓东， 史耀耀，秦现生.复合材料布带缠绕纠偏模糊控制技术研究[J].西北工业大学学报，2014，32（3）：464-469.

[6]史耀耀，袁烨，徐文秀.基于数字 PID 控制的智能纠偏系统设计[J].机械制造，2009，47（7）：32-34.

[7]朱章.物料纠偏系统的设计[D].武汉：武汉理工大学，2011.

[8]张培娟.对带材收卷过程中正弦式跑偏的跟踪控制[D].杭州：杭州电子科技大学，2013.

[9]柯洋.柔性膜卷绕纠偏控制机理与算法研究[D].武汉：华中科技大学，2017.

[10]乔海洋.火箭发动机壳体缠绕纤维带智能纠偏控制系统设计[D].武汉：武汉理工大学，2006.

[11]黄蒙.薄膜卷材纠偏控制系统设计与研究[D].武汉：武汉理工大学，2013.

[12]成卫雄.基于直流无刷电机的纠偏控制系统设计与实现[D].武汉：武汉理工大学，2012.

[13]杨静.锂电池极片涂布设备控制系统设计[D].哈尔滨：哈尔滨工程大学，2017.

[14]李士勇.模糊控制[M].哈尔滨：哈尔滨工业大学出版社，2011.

第一作者简介：肖扬（1996-），男，硕士研究生，研究领域为自动控制。

※通讯作者简介：侯增选（1964-），男，教授，博士生导师，研究领域为自动化缠绕成型工艺与装备研制等。

（编辑：王智圣）